5.4E: Exercícios para a Seção 5.4

Last updated
Save as PDF

Page ID: 187979

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 6, use fórmulas básicas de integração para calcular as seguintes antiderivadas.

1)$\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx$

Resposta: $\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx=∫x^{1/2}\,dx−∫x^{−1/2}\,dx=\frac{2}{3}x^{3/2}+C_1−2x^{1/2+}C_2=\frac{2}{3}x^{3/2}−2x^{1/2}+C$

2)$\displaystyle ∫\left(e^{2x}−\frac{1}{2}e^{x/2}\right)\,dx$

3)$\displaystyle ∫\frac{dx}{2x}$

Resposta: $\displaystyle ∫\frac{dx}{2x}=\frac{1}{2}\ln|x|+C$

4)$\displaystyle ∫\frac{x−1}{x^2}\,dx$

5)$\displaystyle ∫^π_0(\sin x−\cos x)\,dx$

Resposta: $\displaystyle ∫^π_0\sin x\,dx−∫^π_0\cos x\,dx=−\cos x\big|^π_0−(\sin x)\big|^π_0=(−(−1)+1)−(0−0)=2$

6)$\displaystyle ∫^{π/2}_0(x−\sin x)\,dx$

7) Escreva uma integral que expresse o aumento no perímetro$P(s)$ de um quadrado quando seu comprimento lateral$s$ aumenta de 2 unidades para 4 unidades e avalie a integral.

Resposta: $P(s)=4s,$então$\dfrac{dP}{ds}=4$ e$\displaystyle ∫^4_24\,ds=8.$

8) Escreva uma integral que quantifique a mudança na área$A(s)=s^2$ de um quadrado quando o comprimento do lado dobra de$S$ unidades para$2S$ unidades e avalie a integral.

9) Um$N$ -gon regular (um polígono de$N$ -lados com lados que têm o mesmo comprimento$s$, como um pentágono ou hexágono) tem perímetro$Ns.$ Escreva uma integral que expresse o aumento no perímetro de um$N$ -gon regular quando o comprimento de cada lado aumenta de 1 unidade para 2 unidades e avalie a integral.

Resposta: $\displaystyle ∫^2_1N\,ds=N$

10) A área de um pentágono regular com comprimento lateral$a>0$ é$pa^2$ com$p=\frac{1}{4}\sqrt{5+\sqrt{5+2\sqrt{5}}}$. O Pentágono em Washington, DC, tem lados internos de 360 pés de comprimento e lados externos de 920 pés de comprimento. Escreva uma integral para expressar a área do telhado do Pentágono de acordo com essas dimensões e avalie essa área.

11) Um dodecaedro é um sólido platônico com uma superfície que consiste em 12 pentágonos, cada um com a mesma área. Em quanto a área da superfície de um dodecaedro aumenta à medida que o comprimento lateral de cada pentágono dobra de 1 unidade para 2 unidades?

Resposta: $p$Como no exercício anterior, cada um dos 12 pentágonos aumenta em área de$2p$ até$4p$ unidades, então o aumento líquido na área do dodecaedro é de$36p$ unidades.

12) Um icosaedro é um sólido platônico com uma superfície que consiste em 20 triângulos equiláteros. Em quanto a área da superfície de um icosaedro aumenta à medida que o comprimento lateral de cada triângulo dobra de uma unidade para$2a$ unidades?

13) Escreva uma integral que quantifique a mudança na área da superfície de um cubo quando seu comprimento lateral dobra de$s$ unidade para$2s$ unidades e avalie a integral.

Resposta: $\displaystyle 18s^2=6∫^{2s}_s 2x\,dx$

14) Escreva uma integral que quantifique o aumento no volume de um cubo quando o comprimento lateral dobra de$s$ unidade para$2s$ unidades e avalie a integral.

15) Escreva uma integral que quantifique o aumento na área da superfície de uma esfera à medida que seu raio dobra de$R$ unidade para$2R$ unidades e avalie a integral.

Resposta: $\displaystyle 12πR^2=8π∫^{2R}_Rr\,dr$

16) Escreva uma integral que quantifique o aumento no volume de uma esfera à medida que seu raio dobra de$R$ unidade para$2R$ unidades e avalie a integral.

17) Suponha que uma partícula se mova ao longo de uma linha reta com velocidade$v(t)=4−2t,$ onde$0≤t≤2$ (em metros por segundo). Encontre o deslocamento no tempo$t$ e a distância total percorrida até$t=2.$

Resposta: $\displaystyle d(t)=∫^t_0v(s)\,ds=4t−t^2.$A distância total é$d(2)=4$ m.

18) Suponha que uma partícula se mova ao longo de uma linha reta com velocidade definida por$v(t)=t^2−3t−18,$ onde$0≤t≤6$ (em metros por segundo). Encontre o deslocamento no tempo$t$ e a distância total percorrida até$t=6.$

19) Suponha que uma partícula se mova ao longo de uma linha reta com velocidade definida por$v(t)=|2t−6|,$ onde$0≤t≤6$ (em metros por segundo). Encontre o deslocamento no tempo$t$ e a distância total percorrida até$t=6.$

Resposta: $\displaystyle d(t)=∫^t_0v(s)\,ds.$Para$t<3,\;d(t)=∫^t_0(6−2t)\,dt=6t−t^2.$ Para$\displaystyle t>3,\;d(t)=d(3)+∫^t_3(2t−6)\,dt=9+(t^2−6t).$ A distância total é$d(6)=9$ m.

20) Suponha que uma partícula se mova ao longo de uma linha reta com aceleração definida por$a(t)=t−3,$ onde$\displaystyle 0≤t≤6$ (em metros por segundo). Encontre a velocidade e o deslocamento no tempo$t$ e a distância total percorrida até$t=6$ se$v(0)=3$ e$ d(0)=0.$

21) Uma bola é lançada para cima de uma altura de 1,5 m a uma velocidade inicial de 40 m/seg. A aceleração resultante da gravidade é$−9.8\, \text{m/sec}^2.$ negligenciar a resistência do ar, resolver a velocidade$v(t)$ e a altura$h(t)$ da bola$t$ segundos depois de ser lançada e antes de retornar ao solo.

Resposta: $v(t)=40−9.8t;\; h(t)=1.5+40t−4.9t^2$m/s

22) Uma bola é lançada para cima de uma altura de 3 m a uma velocidade inicial de 60 m/seg. A aceleração resultante da gravidade é$−9.8 \, \text{m/sec}^2$. Negligenciando a resistência do ar, resolva a velocidade$v(t)$ e a altura$h(t)$ da bola$t$ segundos depois de ser lançada e antes que ela retorne ao solo.

23) A área$A(t)$ de uma forma circular está crescendo a uma taxa constante. Se a área aumentar de$4π$ unidades para$9π$ unidades entre os tempos$t=2$ e$t=3,$ encontrar a mudança líquida no raio durante esse tempo.

Resposta: O aumento líquido é de 1 unidade.

24) Um balão esférico está sendo inflado a uma taxa constante. Se o volume do balão mudar de$36π \text{ in}^3$ para$288π \text{ in}^3$ entre o tempo$t=30$ e os$t=60$ segundos, encontre a mudança líquida no raio do balão durante esse tempo.

25) A água flui para um tanque cônico com área de seção transversal$πx^2$ em altura$x$ e volume$\frac{πx^3}{3}$ até altura.$x.$ Se a água fluir para o tanque a uma taxa de 1,$\text{m}^3\text{/min},$ encontre a altura da água no tanque após 5 min. Encontre a mudança na altura entre 5 min e 10 min.

Resposta: Em$t=5$, a altura da água é$x=\left(\frac{15}{π}\right)^{1/3}$ m. A mudança líquida na altura de$t=5$ para$t=10$ é$\left(\left(\frac{30}{π}\right)^{1/3}−\left(\frac{15}{π}\right)^{1/3}\right)$ m.

26) Um tanque cilíndrico horizontal tem uma área de seção transversal a$x$ metros de$A(x)=4(6x−x^2)\,\text{m}^2$ altura acima do fundo quando$x≤3.$

a. O volume$V$ entre alturas$a$ e$b$ é$\displaystyle ∫^b_aA(x)\,dx.$ Encontre o volume em alturas entre 2 m e 3 m.

b. Suponha que o óleo esteja sendo bombeado para o tanque a uma taxa de 50 L/min. Usando a regra da corrente,$\dfrac{dx}{dt}=\dfrac{dx}{dV}\dfrac{dV}{dt},$ a quantos metros por minuto a altura do óleo no tanque está mudando, expressa em termos de$x,$ quando a altura está em$x$ metros?

c. Quanto tempo leva para encher o tanque até 3 m a partir de um nível de enchimento de 2 m?

27) A tabela a seguir lista a energia elétrica em gigawatts—a taxa na qual a energia é consumida—usada em uma determinada cidade por diferentes horas do dia, em um período típico de 24 horas, com a hora 1 correspondendo à meia-noite à 1h.

Hora	Poder	Hora	Poder
1	28	13	48
2	25	14	49
3	24	15	49
4	23	16	50
5	24	17	50
6	27	18	50
7	29	19	46
8	32	20	43
9	34	21	42
10	39	22	40
11	42	23	37
12	46	24	34

Encontre a quantidade total de energia em gigawatts-hora (GW-h) consumida pela cidade em um período típico de 24 horas.

Resposta: O consumo diário total de energia é estimado como a soma das taxas de energia por hora, ou 911 GW-h.

28) O uso médio de energia elétrica residencial (em centenas de watts) por hora é dado na tabela a seguir.

Hora	Poder	Hora	Poder
1	8	13	12
2	6	14	13
3	5	15	14
4	4	16	15
5	5	17	17
6	6	18	19
7	7	19	18
8	8	20	17
9	9	21	16
10	10	22	16
11	10	23	13
12	11	24	11

a. Calcule a energia total média usada em um dia em quilowatts-hora (kWh).

b. Se uma tonelada de carvão gera 1842 kWh, quanto tempo leva para uma residência média queimar uma tonelada de carvão?

c. Explique por que os dados podem caber em um gráfico do formulário$p(t)=11.5−7.5\sin\left(\frac{πt}{12}\right).$

29) Os dados na tabela a seguir são usados para estimar a potência média produzida por Peter Sagan para cada um dos últimos 18 segundos da Etapa 1 do Tour de France 2012.

Segundo	Watts	Segundo	Watts
1	600	10	1200
2	500	11	1170
3	575	12	1125
4	1050	13	1100
5	925	14	1075
6	950	15	1000
7	1050	16	950
8	950	17	900
9	1100	18	780

Fonte média de saída de energia: sportsexercisengineering.com

Estime a energia líquida usada em quilojoules (kJ), observando que 1W = 1 J/s e a potência média de saída de Sagan durante esse intervalo de tempo.

Resposta: $17$kJ

30) Os dados na tabela a seguir são usados para estimar a potência média produzida por Peter Sagan para cada intervalo de 15 minutos da Etapa 1 do Tour de France 2012.

Minutos	Watts	Minutos	Watts
15	200	165	170
30	180	180	220
45	190	195	140
60	230	210	225
75	240	225	170
90	210	240	10
105	210	255	200
1120	220	270	220
135	210	285	250
150	150	300	400

Fonte média de saída de energia: sportsexercisengineering.com

Estime a energia líquida usada em quilojoules, observando que 1W = 1 J/s.

31) A distribuição da renda em 2012 nos Estados Unidos em incrementos de $5000 é dada na tabela a seguir. A késima linha indica a porcentagem de famílias com renda entre$$5000xk$$5000xk+4999$ e. A linha$k=40$ contém todas as famílias com renda entre $200.000 e $250.000 e$k=41$ representa todas as famílias com renda superior a $250.000.

0	3.5	21	1,5
1	4.1	22	1.4
2	5.9	23	1.3
3	5.7	24	1.3
4	5.9	25	1.1
5	5.4	26	1,0
6	5.5	27	0,75
7	5.1	28	0,8
8	4.8	29	1,0
9	4.1	30	0,6
10	4.3	31	0,6
11	3.5	32	.5
12	3.7	33	0,5
13	3.2	34	0,4
14	3,0	35	0,3
15	2.8	36	0,3
16	2,5	37	0,3
17	2.2	38	0,2
18	2.2	39	1.8
19	1.8	40	2.3
20	2.1	41

Distribuições de renda Fonte: http://www.census.gov/prod/2013pubs/p60-245.pdf

a. Estime a porcentagem de famílias nos EUA em 2012 com renda inferior a $55.000.

b. Qual porcentagem de famílias tinha renda superior a $85.000?

c. Faça um gráfico dos dados e tente ajustar sua forma à de um gráfico do formulário, de forma$a(x+c)e^{−b(x+e)}$ adequada$a,\, b,\, c.$

Resposta

a. 54,3%;
b. 27,00%;
c. A curva no gráfico a seguir é$2.35(t+3)e^{−0.15(t+3)}.$

$Um gráfico dos dados e uma função aproximando os dados. A função é uma aproximação muito próxima.$

32) A lei da gravidade de Newton afirma que a força gravitacional exercida por um objeto de massa$M$ e outro de massa$m$ com centros separados por uma distância r é$F=G\dfrac{mM}{r^2}$, com$G$ uma constante empírica$G=6.67x10^{−11}\,\text{m}^3/(\text{kg⋅s}^2)$. O trabalho realizado por uma força variável em um intervalo$ [a,b]$ é definido como$\displaystyle W=∫^b_aF(x)\,dx$. Se a Terra tiver massa$5.97219×10^{24}$ e raio de 6371 km, calcule a quantidade de trabalho para elevar um satélite meteorológico polar de massa de 1400 kg à sua altitude orbital de 850 km acima da Terra.

33) Para um determinado veículo a motor, a desaceleração máxima alcançável da frenagem é aproximadamente$7 \text{ m/sec}^2$ em concreto seco. No asfalto úmido, é aproximadamente$2.5 \text{ m/sec}^2.$ Dado que 1 mph corresponde a 0,447 m/seg, determine a distância total que um carro percorre em metros em concreto seco após a aplicação dos freios até parar completamente se a velocidade inicial for 67 mph (30 m/seg) ou se a velocidade inicial de frenagem for 56 mph (56 mph) (25 m/seg). Encontre as distâncias correspondentes se a superfície for de asfalto úmido escorregadio.

Resposta: Em condições secas, com velocidade inicial$v_0=30$ m/s$D=64.3$ e, se$v_0=25,\; D=44.64$. Em condições úmidas$v_0=30$, se$D=180$ e se$v_0=25,\;D=125.$

34) John é um homem de 25 anos que pesa 160 libras. Ele queima$500−50t$ calorias/hora enquanto anda de bicicleta por$t$ horas. Se um biscoito de aveia tem 55 cal e John come$4t$ biscoitos durante a$t^{\text{th}}$ hora, quantas calorias líquidas ele perdeu depois de 3 horas andando de bicicleta?

35) Sandra é uma mulher de 25 anos que pesa 120 libras. Ela queima$300−50t$ cal/h enquanto caminha na esteira por$t$ horas. Sua ingestão calórica ao beber Gatorade é de$100t$ calorias durante a$t^{\text{th}}$ hora. Qual é a diminuição líquida de calorias dela depois de caminhar por 3 horas?

Resposta: 225 kcal

36) Um veículo motorizado tem uma eficiência máxima de 33 mpg a uma velocidade de cruzeiro de 40 mph. A eficiência cai a uma taxa de 0,1 mpg/mph entre 40 mph e 50 mph, e a uma taxa de 0,4 mpg/mph entre 50 mph e 80 mph. Qual é a eficiência em milhas por galão se o carro estiver viajando a 50 mph? Qual é a eficiência em milhas por galão se o carro estiver viajando a 80 mph? Se a gasolina custa $3,50/gal, qual é o custo do combustível para dirigir 50 milhas a 40 mph, a 50 mph e a 80 mph?

37) Embora alguns motores sejam mais eficientes com uma determinada potência do que outros, em média, a eficiência de combustível diminui com a potência a uma taxa de$1/25$ mpg/cavalos de potência. Se um motor típico de 50 cavalos de potência tem uma eficiência média de combustível de 32 mpg, qual é a eficiência média de combustível de um motor com a seguinte potência: 150, 300, 450?

Resposta: $ E(150)=28,\;E(300)=22,\;E(450)=16$

38) [T] A tabela a seguir lista o cronograma de 2013 do imposto de renda federal versus renda tributável.

Faixa de renda tributável	O imposto é...	... Do valor acima
$0 — $8925	10%	$0
$8925 — $36.250	892,50 US$ + 15%	$8925
$36.250 — $87.850	4.991,25 US$ + 25%	$36.250
$87.850 — $183.250	17.891,25$ + 28%	$87.850
$183.250 — $398.350	$44.603,25 + 33%	$183.250
$398.350 — $400.000	$115.586,25 + 35%	$398.350
> $400.000	$116.163,75 + 39,6%	$400.000

Imposto de renda federal versus renda tributável Fonte: http://www.irs.gov/pub/irs-prior/i1040tt--2013.pdf.

Suponha que Steve acabou de receber um aumento de $10.000. Quanto desse aumento resta após os impostos federais se o salário de Steve antes de receber o aumento fosse de $40.000? Se fosse $90.000? Se fosse $385.000?

39) [T] A tabela a seguir fornece dados hipotéticos sobre o nível de serviço de uma determinada rodovia.

Faixa de velocidade da estrada (mph)	Veículos por hora por faixa	Faixa de densidade (veículos/mi)
>60	<600	<10
60-57	300-1000	10-20
57-54	1000-1500	20-30
57-54	1500-1900	30-45
46-30	1900-2100	48-70
<30	Instável	70-200

a. Faça um gráfico de veículos por hora por faixa no$x$ eixo -e a velocidade da rodovia no$y$ eixo -.

b. Calcule a diminuição média da velocidade (em milhas por hora) por unidade de aumento no congestionamento (veículos por hora por faixa) à medida que o último aumenta de 600 para 1000, de 1000 para 1500 e de 1500 para 2100. A diminuição de milhas por hora depende linearmente do aumento de veículos por hora por faixa?

c. Traçar minutos por milha (60 vezes o inverso de milhas por hora) em função de veículos por hora por faixa. Essa função é linear?

Resposta

uma.

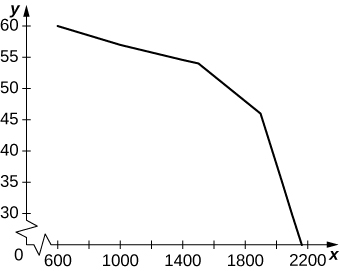
$Um gráfico dos dados fornecidos, que diminui de forma aproximadamente côncava para baixo de 600 para 2200.$

b. Entre 600 e 1000, a diminuição média de veículos por hora por faixa é de −0,0075. Entre 1000 e 1500, é −0,006 por veículo por hora por faixa, e entre 1500 e 2100 é −0,04 veículos por hora por faixa.

c.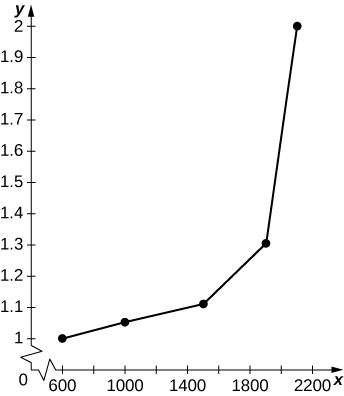

$Um gráfico de dados fornecidos, mostrando que os minutos por milha aumentam dramaticamente à medida que os veículos por hora chegam a 2000.$

O gráfico não é linear, com minutos por milha aumentando dramaticamente à medida que veículos por hora por faixa atingem 2000.

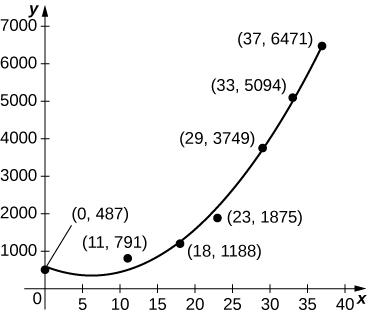
Para os próximos dois exercícios, use os dados da tabela a seguir, que mostra as populações de águias carecas de 1963 a 2000 nos Estados Unidos continentais.

Ano	População de pares reprodutores de águias carecas
1963	487
1974	791
1981	1188
1986	1875
1992	3749
1996	5094
2000	6471

População reprodutora de pares de águias carecas Fonte: http://www.fws.gov/Midwest/eagle/pop... /chtofprs.html.

40) [T] O gráfico abaixo traça a quadrática em$p(t)=6.48t^2−80.31t+585.69$ relação aos dados na tabela anterior, normalizada para que$t=0$ corresponda a 1963. Estime o número médio de águias carecas por ano presentes nos 37 anos calculando o valor médio de$p$ mais de$[0,37].$

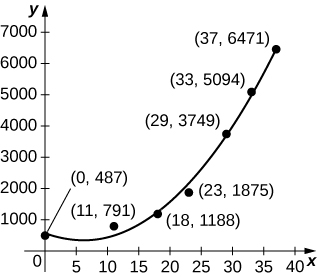
$Um gráfico dos dados e uma função quadrática que se aproxima deles.$

41) [T] O gráfico abaixo traça o cúbico em$p(t)=0.07t^3+2.42t^2−25.63t+521.23$ relação aos dados da tabela anterior, normalizados de forma que$t=0$ corresponda a 1963. Estime o número médio de águias carecas por ano presentes nos 37 anos calculando o valor médio de$p$ mais de$[0,37].$

$Um gráfico dos dados e uma função cúbica que se aproxima deles.$

Resposta: $\displaystyle \frac{1}{37}∫^{37}_0p(t)\,dt=\frac{0.07(37)^3}{4}+\frac{2.42(37)^2}{3}−\frac{25.63(37)}{2}+521.23≈2037$

Solução:

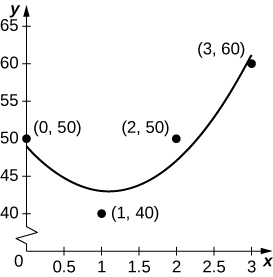
42) [T] Suponha que você faça uma viagem e registre sua velocidade a cada meia hora, conforme compilado na tabela a seguir. O melhor ajuste quadrático aos dados é$q(t)=5x^2−11x+49$ mostrado no gráfico anexo. Integre$q$ para estimar a distância total percorrida nas 3 horas.

Tempo (hora)	Velocidade (m [h)
0 (início)	50
1	40
2	50
3	60

$Um gráfico dos dados e uma curva destinados a aproximá-los.$

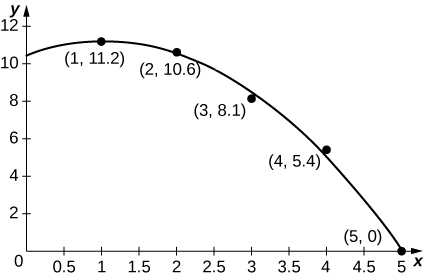
Quando um carro acelera, ele não acelera a uma taxa constante; em vez disso, a aceleração é variável. Para os exercícios a seguir, use a tabela a seguir, que contém a aceleração medida a cada segundo quando um motorista entra em uma rodovia.

Tempo (seg)	Aceleração (mph/seg)
1	11.2
2	10.6
3	8.1
4	5.4
5	0

43) [T] O gráfico anexo representa graficamente o melhor ajuste quadrático$a(t)=−0.70t^2+1.44t+10.44$,, para os dados da tabela anterior. Calcule o valor médio de$a(t)$ para estimar a aceleração média entre$t=0$ e$t=5.$

$Um gráfico dos dados e uma curva que se aproximam muito dos dados.$

Resposta: A aceleração média é$\displaystyle A=\frac{1}{5}∫^5_0a(t)\,dt=−\frac{0.7(5^2)}{3}+\frac{1.44(5)}{2}+10.44≈8.2$ mph/s

44) [T] Usando a equação de aceleração do exercício anterior, encontre a equação de velocidade correspondente. Supondo que a velocidade final seja 0 mph, encontre a velocidade no momento$t=0.$

45) [T] Usando sua equação de velocidade do exercício anterior, encontre a equação de distância correspondente, supondo que sua distância inicial seja 0 mi. Até onde você viajou enquanto acelerava seu carro? (Dica: você precisará converter as unidades de tempo.)

Resposta: $\displaystyle d(t)=∫^1_0|v(t)|\,dt=∫^t_0\left(\frac{7}{30}t^3−0.72t^2−10.44t+41.033\right)\,dt=\frac{7}{120}t^4−0.24t^3−5.22t^3+41.033t.$Depois,$d(5)≈81.12 \,\text{mph} × \text{sec}≈119$ pés.

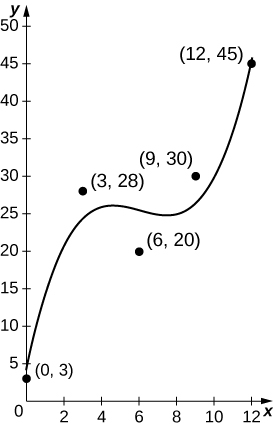
46) [T] O número de hambúrgueres vendidos em um restaurante ao longo do dia é dado na tabela a seguir, com o gráfico a seguir representando o melhor ajuste cúbico aos dados,$b(t)=0.12t^3−2.13t^3+12.13t+3.91,$$t=0$ correspondendo às 9h e$t=12$ correspondendo às 21h. Calcule o valor médio de$b(t)$ até estime o número médio de hambúrgueres vendidos por hora.

Horas depois da meia-noite	Nº de hambúrgueres vendidos
9	3
12	28
15	20
18	30
21	45

$Um mapa dos dados e uma curva destinados a aproximar os dados.$

47) [T] Uma atleta passa por um detector de movimento, que registra sua velocidade, conforme mostrado na tabela a seguir. O melhor ajuste linear para esses dados$ℓ(t)=−0.068t+5.14$,, é mostrado no gráfico anexo. Use o valor médio$ℓ(t)$ entre$t=0$ e$t=40$ para estimar a velocidade média do corredor.

Minutos	Velocidade (m/seg)
0	5
10	4.8
20	3.6
30	3,0
40	2,5

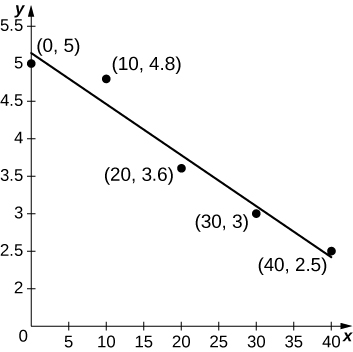
$Um gráfico dos dados e uma linha para aproximar os dados.$

Resposta: $\displaystyle \tfrac{1}{40} ∫^{40}_0(−0.068t+5.14)\,dt=−\frac{0.068(40)}{2}+5.14=3.78$ m/sec