4.10: Antiderivados
- Page ID
- 188324
- Encontre a antiderivada geral de uma determinada função.
- Explique os termos e a notação usados para uma integral indefinida.
- Declare a regra de potência para integrais.
- Use a antidiferenciação para resolver problemas simples de valor inicial.
Neste ponto, vimos como calcular derivadas de muitas funções e fomos apresentados a uma variedade de suas aplicações. Agora fazemos uma pergunta que inverte esse processo: Dada uma função\(f\), como podemos encontrar uma função com a derivada\(f\) e por que estaríamos interessados em tal função?
Respondemos à primeira parte dessa pergunta definindo antiderivadas. A antiderivada de uma função\(f\) é uma função com uma derivada\(f\). Por que estamos interessados em antiderivativos? A necessidade de antiderivadas surge em muitas situações, e examinamos vários exemplos ao longo do restante do texto. Aqui, examinamos um exemplo específico que envolve movimento retilíneo. Em nosso exame em Derivadas do movimento retilíneo, mostramos que dada a função\(s(t)\) de posição de um objeto, sua função de velocidade\(v(t)\) é a derivada de\(s(t)\) —isto é,\(v(t)=s′(t)\). Além disso, a aceleração\(a(t)\) é a derivada da velocidade,\(v(t)\) ou seja,\(a(t)=v′(t)=s''(t)\). Agora, suponha que recebamos uma função de aceleração\(a\), mas não a função de velocidade\(v\) ou a função de posição\(s\). \(a(t)=v′(t)\)Pois, determinar a função de velocidade exige que encontremos uma antiderivada da função de aceleração. Então, uma vez que\(v(t)=s′(t),\) determinar a função de posição exige que encontremos uma antiderivada da função de velocidade. O movimento retilíneo é apenas um caso em que surge a necessidade de antiderivadas. Veremos muitos outros exemplos ao longo do restante do texto. Por enquanto, vamos examinar a terminologia e a notação de antiderivadas e determinar as antiderivadas para vários tipos de funções. Examinamos várias técnicas para encontrar antiderivadas de funções mais complicadas posteriormente no texto (Introdução às técnicas de integração).
O inverso da diferenciação
Neste ponto, sabemos como encontrar derivadas de várias funções. Agora fazemos a pergunta oposta. Dada uma função\(f\), como podemos encontrar uma função com derivada\(f\)? Se pudermos encontrar uma função\(F\) com derivada,\(f,\) chamamos\(F\) de antiderivada de\(f\).
Uma função\(F\) é uma antiderivada da função\(f\) se
\[F′(x)=f(x) \nonumber \]
para todos\(x\) no domínio de\(f\).
Considere a função\(f(x)=2x\). Conhecendo a regra de poder da diferenciação, concluímos que\(F(x)=x^2\) é uma antiderivada de uma\(f\) vez\(F′(x)=2x\).
Existem outros antiderivados do\(f\)?
Sim; como a derivada de qualquer constante\(C\) é zero, também\(x^2+C\) é uma antiderivada de\(2x\). Portanto,\(x^2+5\) e também\(x^2−\sqrt{2}\) são antiderivados.
Existem outras que não são da forma\(x^2+C\) de alguma constante\(C\)?
A resposta é não. A partir do Corolário 2 do Teorema do Valor Médio, sabemos que se\(F\) e\(G\) são funções diferenciáveis de tal forma que\(F′(x)=G′(x),\), então,\(F(x)−G(x)=C\) para alguma constante\(C\). Esse fato leva ao seguinte teorema importante.
\(F\)Seja uma antiderivada de\(f\) mais de um intervalo\(I\). Em seguida,
- para cada constante\(C\), a função também\(F(x)+C\) é uma antiderivada de\(f\) over\(I\);
- se\(G\) é uma antiderivada de\(f\) over\(I\), há uma constante\(C\) para a qual\(G(x)=F(x)+C\) over\(I\).
Em outras palavras, a forma mais geral da antiderivada de\(f\) over\(I\) é\(F(x)+C\).
Usamos esse fato e nosso conhecimento de derivadas para encontrar todas as antiderivadas para várias funções.
Para cada uma das funções a seguir, encontre todas as antiderivadas.
- \(f(x)=3x^2\)
- \(f(x)=\dfrac{1}{x}\)
- \(f(x)=\cos x\)
- \(f(x)=e^x\)
Solução:
a. Porque
\[\dfrac{d}{dx}\left(x^3\right)=3x^2 \nonumber \]
então\(F(x)=x^3\) é uma antiderivada de\(3x^2\). Portanto, toda antiderivada de\(3x^2\) é da forma\(x^3+C\) de alguma constante\(C\), e cada função da forma\(x^3+C\) é uma antiderivada de\(3x^2\).
b. Esquerda\(f(x)=\ln |x|.\)
Para\(x>0,\; f(x)=\ln |x|=\ln (x)\) e
\[\dfrac{d}{dx}\Big(\ln x\Big)=\dfrac{1}{x}. \nonumber \]
Para\(x<0,\; f(x)=\ln |x|=\ln (−x)\) e
\[\dfrac{d}{dx}\Big(\ln (−x)\Big)=−\dfrac{1}{−x}=\dfrac{1}{x}. \nonumber \]
Portanto,
\[\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}. \nonumber \]
Assim,\(F(x)=\ln |x|\) é uma antiderivada de\(\dfrac{1}{x}\). Portanto, toda antiderivada de\(\dfrac{1}{x}\) é da forma\(\ln |x|+C\) de alguma constante\(C\) e cada função da forma\(\ln |x|+C\) é uma antiderivada de\(\dfrac{1}{x}\).
c. Nós temos
\[\dfrac{d}{dx}\Big(\sin x\Big)=\cos x, \nonumber \]
então\(F(x)=\sin x\) é uma antiderivada de\(\cos x\). Portanto, toda antiderivada de\(\cos x\) é da forma\(\sin x+C\) de alguma constante\(C\) e cada função da forma\(\sin x+C\) é uma antiderivada de\(\cos x\).
d. Desde
\[\dfrac{d}{dx}\left(e^x\right)=e^x, \nonumber \]
então\(F(x)=e^x\) é uma antiderivada de\(e^x\). Portanto, toda antiderivada de\(e^x\) é da forma\(e^x+C\) de alguma constante\(C\) e cada função da forma\(e^x+C\) é uma antiderivada de\(e^x\).
Encontre todos os antiderivados do\(f(x)=\sin x\).
- Dica
-
Qual função tem uma derivada de\(\sin x\)?
- Resposta
-
\(F(x) = −\cos x+C\)
Integrais indefinidos
Agora examinamos a notação formal usada para representar antiderivadas e examinamos algumas de suas propriedades. Essas propriedades nos permitem encontrar antiderivadas de funções mais complicadas. Dada uma função\(f\), usamos a notação\(f′(x)\) ou\(\dfrac{df}{dx}\) para denotar a derivada de\(f\). Aqui, introduzimos a notação para antiderivadas. Se\(F\) é uma antiderivada de\(f\), dizemos que\(F(x)+C\) é a antiderivada mais geral de\(f\) e escrevemos
\[\int f(x)\,dx=F(x)+C.\nonumber \]
O símbolo\(\displaystyle \int \) é chamado de sinal integral e\(\displaystyle \int f(x)\,dx\) é chamado de integral indefinido de\(f\).
Dada uma função\(f\), a integral indefinida de\(f\), denotada
\[\int f(x)\,dx, \nonumber \]
é a antiderivada mais geral de\(f\). Se\(F\) for uma antiderivada de\(f\), então
\[\int f(x)\,dx=F(x)+C. \nonumber \]
A expressão\(f(x)\) é chamada de integrando e a variável\(x\) é a variável de integração.
Dada a terminologia introduzida nesta definição, o ato de encontrar as antiderivadas de uma função\(f\) é geralmente chamado de integração\(f\).
Para uma função\(f\) e uma antiderivada\(F\), as funções\(F(x)+C\), onde\(C\) está qualquer número real, são frequentemente chamadas de família de antiderivadas de\(f\). Por exemplo, uma vez que\(x^2\) é uma antiderivada de\(2x\) e qualquer antiderivada de\(2x\) é da forma\(x^2+C,\) que escrevemos
\[\int 2x\,dx=x^2+C.\nonumber \]
A coleção de todas as funções da forma\(x^2+C,\) onde\(C\) está qualquer número real, é conhecida como a família de antiderivadas de\(2x\). A figura\(\PageIndex{1}\) mostra um gráfico dessa família de antiderivadas.
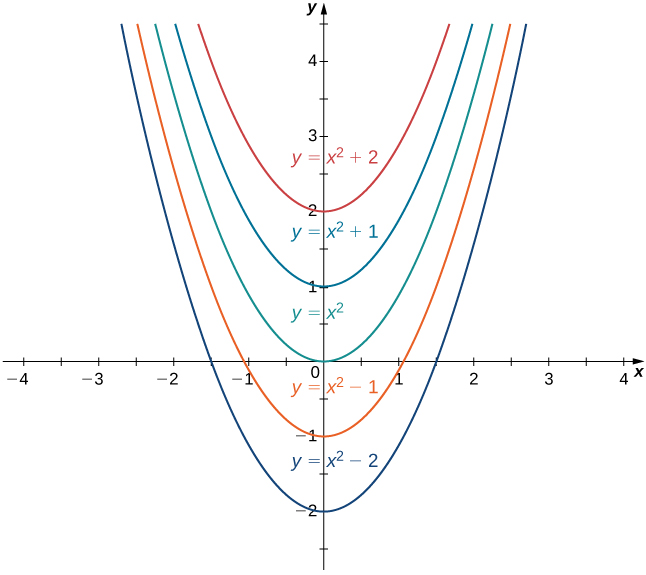
Para algumas funções, a avaliação de integrais indefinidas segue diretamente das propriedades das derivadas. Por exemplo, para\(n≠−1\),
\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C,\)
que vem diretamente de
\(\dfrac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n\).
Esse fato é conhecido como regra de potência para integrais.
Para\(n≠−1,\)
\[\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C. \nonumber \]
A avaliação de integrais indefinidas para algumas outras funções também é um cálculo simples. A tabela a seguir lista as integrais indefinidas para várias funções comuns. Uma lista mais completa aparece no Apêndice B.
| Fórmula de diferenciação | Integral indefinido |
|---|---|
| \(\dfrac{d}{dx}\Big(k\Big)=0\) | \(\displaystyle \int k\,dx=\int kx^0\,dx=kx+C\) |
| \(\dfrac{d}{dx}\Big(x^n\Big)=nx^{n−1}\) | \(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C\)para\(n≠−1\) |
| \(\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}\) | \(\displaystyle \int \dfrac{1}{x}\,dx=\ln |x|+C\) |
| \(\dfrac{d}{dx}\Big(e^x\Big)=e^x\) | \(\displaystyle \int e^x\,dx=e^x+C\) |
| \(\dfrac{d}{dx}\Big(\sin x\Big)=\cos x\) | \(\displaystyle \int \cos x\,dx=\sin x+C\) |
| \(\dfrac{d}{dx}\Big(\cos x\Big)=−\sin x\) | \(\displaystyle \int \sin x\,dx=−\cos x+C\) |
| \(\dfrac{d}{dx}\Big(\tan x\Big)=\sec^2 x\) | \(\displaystyle \int \sec^2 x\,dx=\tan x+C\) |
| \(\dfrac{d}{dx}\Big(\csc x\Big)=−\csc x\cot x\) | \(\displaystyle \int \csc x\cot x\,dx=−\csc x+C\) |
| \(\dfrac{d}{dx}\Big(\sec x\Big)=\sec x\tan x\) | \(\displaystyle \int \sec x\tan x\,dx=\sec x+C\) |
| \(\dfrac{d}{dx}\Big(\cot x\Big)=−\csc^2 x\) | \(\displaystyle \int \csc^2x\,dx=−\cot x+C\) |
| \(\dfrac{d}{dx}\Big(\sin^{−1}x\Big)=\dfrac{1}{\sqrt{1−x^2}}\) | \(\displaystyle \int \dfrac{1}{\sqrt{1−x^2}}=\sin^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\tan^{−1}x\Big)=\dfrac{1}{1+x^2}\) | \(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\tan^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\sec^{−1}|x|\Big)=\dfrac{1}{x\sqrt{x^2−1}}\) | \(\displaystyle \int \dfrac{1}{x\sqrt{x^2−1}}\,dx=\sec^{−1}|x|+C\) |
A partir da definição de integral indefinida de\(f\), sabemos
\[\int f(x)\,dx=F(x)+C\nonumber \]
se e somente se\(F\) for uma antiderivada de\(f\).
Portanto, ao afirmar que
\[\int f(x)\,dx=F(x)+C\nonumber \]
é importante verificar se essa afirmação está correta, verificando se\(F′(x)=f(x).\)
Cada uma das afirmações a seguir é do formato\(\displaystyle \int f(x)\,dx=F(x)+C.\) Verifique se cada afirmação está correta mostrando que\(F′(x)=f(x).\)
- \(\displaystyle\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C\)
- \(\displaystyle\int xe^x\,dx=xe^x−e^x+C\)
Solução:
a. Desde
\(\dfrac{d}{dx}\left(\dfrac{x^2}{2}+e^x+C\right)=x+e^x\),
a declaração
\[\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C \nonumber \]
está correto.
Observe que estamos verificando uma integral indefinida para uma soma. Além disso,\(\dfrac{x^2}{2}\) e\(e^x\) são antiderivadas de\(x\) e\(e^x\), respectivamente, e a soma das antiderivadas é uma antiderivada da soma. Discutiremos esse fato novamente mais tarde nesta seção.
b. Usando a regra do produto, vemos que
\[\dfrac{d}{dx}\left(xe^x−e^x+C\right)=e^x+xe^x−e^x=xe^x. \nonumber \]
Portanto, a declaração
\[\int xe^x\,dx=xe^x−e^x+C \nonumber \]
está correto.
Observe que estamos verificando uma integral indefinida para um produto. O antiderivado não\(xe^x−e^x\) é um produto dos antiderivados. Além disso, o produto de antiderivados, não\(x^2e^x/2\) é um\(xe^x\) antiderivado de
\(\dfrac{d}{dx}\left(\dfrac{x^2e^x}{2}\right)=xe^x+\dfrac{x^2e^x}{2}≠xe^x\).
Em geral, o produto dos antiderivados não é um antiderivado de um produto.
Verifique se\(\displaystyle \int x\cos x\,\,dx=x\sin x+\cos x+C.\)
- Dica
-
Calcular\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big).\)
- Resposta
-
\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big)=\sin x+x\cos x−\sin x=x \cos x\)
Na tabela\(\PageIndex{1}\), listamos as integrais indefinidas para muitas funções elementares. Agora, vamos voltar nossa atenção para avaliar integrais indefinidas para funções mais complicadas. Por exemplo, considere encontrar uma antiderivada de uma soma\(f+g\). No exemplo,\(\PageIndex{2}a\) mostramos que uma antiderivada da soma\(x+e^x\) é dada pela soma, ou\(\dfrac{x^2}{2}+e^x\) seja, uma antiderivada de uma soma é dada pela soma das antiderivadas. Esse resultado não foi específico para esse exemplo. Em geral, se\(F\) e\(G\) são antiderivadas de qualquer função\(f\) e\(g\), respectivamente, então
\(\dfrac{d}{dx}\big(F(x)+G(x)\big)=F′(x)+G′(x)=f(x)+g(x).\)
Portanto,\(F(x)+G(x)\) é uma antiderivada de\(f(x)+g(x)\) e temos
\[ \int \big(f(x)+g(x)\big)\,dx=F(x)+G(x)+C.\nonumber \]
Da mesma forma,
\[ \int \big(f(x)−g(x)\big)\,dx=F(x)−G(x)+C.\nonumber \]
Além disso, considere a tarefa de encontrar uma antiderivada de\(kf(x),\) onde\(k\) está qualquer número real. Desde
\[ \dfrac{d}{dx}\Big(kF(x)\Big)=k\dfrac{d}{dx}\Big(F(x)\Big)=kF′(x)\nonumber \]
para qualquer número real\(k\), concluímos que
\[ \int kf(x)\,dx=kF(x)+C.\nonumber \]
Essas propriedades estão resumidas a seguir.
\(G\)Seja\(F\) e seja antiderivado de\(f\) e\(g\), respectivamente, e\(k\) seja qualquer número real.
Somas e diferenças
\[\int \big(f(x)±g(x)\big)\,dx=F(x)±G(x)+C \nonumber \]
Múltiplos constantes
\[ \int kf(x)\,dx=kF(x)+C \nonumber \]
A partir desse teorema, podemos calcular qualquer integral envolvendo uma soma, diferença ou múltiplo constante de funções com antiderivadas conhecidas. Avaliar integrais envolvendo produtos, quocientes ou composições é mais complicado. (Veja o exemplo\(\PageIndex{2}b\) para ver um exemplo envolvendo uma antiderivada de um produto.) Examinamos e abordamos integrais que envolvem essas funções mais complicadas em Introdução à Integração. No próximo exemplo, examinaremos como usar esse teorema para calcular as integrais indefinidas de várias funções.
Avalie cada uma das seguintes integrais indefinidas:
- \(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx\)
- \(\displaystyle \int \dfrac{x^2+4\sqrt[3]{x}}{x}\,dx\)
- \(\displaystyle \int \dfrac{4}{1+x^2}\,dx\)
- \(\displaystyle \int \tan x\cos x\,dx\)
Solução:
a. Usando propriedades de integrais indefinidas, podemos integrar cada um dos quatro termos no integrando separadamente. Nós obtemos
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx.\)
A partir da segunda parte de Propriedades de integrais indefinidas, cada coeficiente pode ser escrito na frente do sinal integral, que fornece
\(\displaystyle \int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx=5\int x^3\,dx−7\int x^2\,dx+3\int x\,dx+4\int 1\,dx.\)
Usando a regra de potência para integrais, concluímos que
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\dfrac{5}{4}x^4−\dfrac{7}{3}x^3+\dfrac{3}{2}x^2+4x+C.\)
b. Reescreva o integrando como
\(\dfrac{x^2+4\sqrt[3]{x}}{x}=\dfrac{x^2}{x}+\dfrac{4\sqrt[3]{x}}{x}.\)
Em seguida, para avaliar a integral, integre cada um desses termos separadamente. Usando a regra do poder, temos
\ [\ begin {align*}\ int\ left (x+\ dfrac {4} {x^ {2/3}}\ direita)\, dx&=\ int x\, dx+4\ int x^ {−2/3}\, dx\\ [4pt]
&=\ dfrac {1} {2} x^2+4\ dfrac {1} {\ left\ tfrac {−2} {3}\ direita) +1} x^ {(−2/3) +1} +C\\ [4pt]
&=\ dfrac {1} {2} x^2+12x^ {1/3} +C.\ end {align*}\]
c. Usando propriedades de integrais indefinidas, escreva a integral como
\(4\displaystyle \int \dfrac{1}{1+x^2}\,dx.\)
Em seguida, use o fato de que\(\tan^{−1}(x)\) é uma antiderivada de\(\dfrac{1}{1+x^2}\) para concluir que
\(\displaystyle \int \dfrac{4}{1+x^2}\,dx=4\tan^{−1}(x)+C.\)
d. Reescreva o integrando como
\(\tan x\cos x=\dfrac{\sin x}{\cos x}\cdot\cos x=\sin x.\)
Portanto,
\(\displaystyle \int \tan x\cos x\,dx=\int \sin x\,dx=−\cos x+C.\)
Avalie\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx\).
- Dica
-
Integre cada termo no integrando separadamente, fazendo uso da regra de potência.
- Resposta
-
\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx = \quad x^4−\dfrac{5}{3}x^3+\dfrac{1}{2}x^2−7x+C\)
Problemas de valor inicial
Examinaremos técnicas para integrar uma grande variedade de funções envolvendo produtos, quocientes e composições posteriormente no texto. Aqui, recorremos a um uso comum de antiderivadas que surge com frequência em muitas aplicações: resolver equações diferenciais.
Uma equação diferencial é uma equação que relaciona uma função desconhecida e uma ou mais de suas derivadas. A equação
é um exemplo simples de uma equação diferencial. Resolver essa equação significa encontrar uma função\(y\) com uma derivada\(f\). Portanto, as soluções da Equação\ ref {diffeq1} são as antiderivadas de\(f\). Se\(F\) for uma antiderivada de\( f\), cada função da forma\( y=F(x)+C\) é uma solução dessa equação diferencial. Por exemplo, as soluções de
são dadas por
Às vezes, estamos interessados em determinar se uma determinada curva de solução passa por um determinado ponto,\( (x_0,y_0)\) ou seja,\( y(x_0)=y_0\). O problema de encontrar uma função\(y\) que satisfaça uma equação diferencial
com a condição adicional
é um exemplo de um problema de valor inicial. A condição\( y(x_0)=y_0\) é conhecida como condição inicial. Por exemplo, procurando uma função\( y\) que satisfaça a equação diferencial
e a condição inicial
é um exemplo de um problema de valor inicial. Como as soluções da equação diferencial são\( y=2x^3+C,\) encontrar uma função\(y\) que também satisfaça a condição inicial, precisamos encontrar\(C\) isso\(y(1)=2(1)^3+C=5\). A partir dessa equação, vemos isso\( C=3\) e concluímos que\( y=2x^3+3\) é a solução desse problema de valor inicial, conforme mostrado no gráfico a seguir.
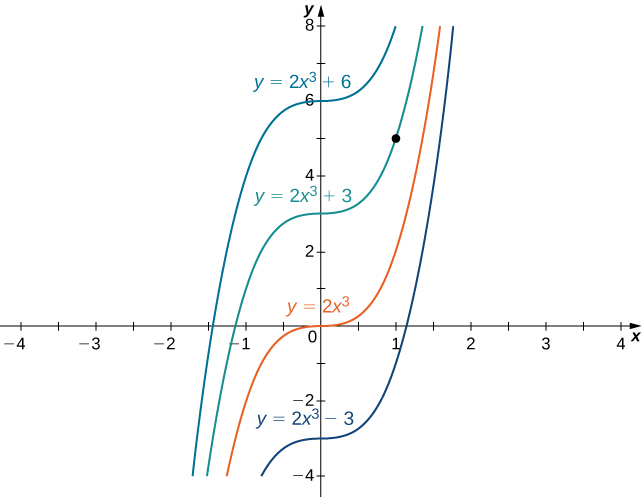
Resolva o problema do valor inicial
\[\dfrac{dy}{dx}=\sin x,\quad y(0)=5.\nonumber \]
Solução
Primeiro, precisamos resolver a equação diferencial. Se\(\dfrac{dy}{dx}=\sin x\), então
\[y=\displaystyle \int \sin(x)\,dx=−\cos x+C.\nonumber \]
Em seguida, precisamos procurar uma solução\(y\) que satisfaça a condição inicial. A condição inicial\(y(0)=5\) significa que precisamos de uma constante\(C\) tal que\(−\cos x+C=5.\) Portanto,
\[C=5+\cos(0)=6.\nonumber \]
A solução do problema do valor inicial é\(y=−\cos x+6.\)
Resolva o problema do valor inicial\(\dfrac{dy}{dx}=3x^{−2},\quad y(1)=2\).
- Dica
-
Encontre todos os antiderivados de\(f(x)=3x^{−2.}\)
- Responda
-
\(y=−\dfrac{3}{x}+5\)
Problemas de valor inicial surgem em muitos aplicativos. Em seguida, consideramos um problema no qual um motorista aciona os freios em um carro. Estamos interessados em saber quanto tempo leva para o carro parar. Lembre-se de que a função de velocidade\(v(t)\) é a derivada de uma função de posição\(s(t),\) e a aceleração\(a(t)\) é a derivada da função de velocidade. Em exemplos anteriores do texto, poderíamos calcular a velocidade a partir da posição e, em seguida, calcular a aceleração a partir da velocidade. No próximo exemplo, trabalhamos ao contrário. Dada uma função de aceleração, calculamos a função de velocidade. Em seguida, usamos a função de velocidade para determinar a função de posição.
Um carro está viajando a uma taxa de\(88\) pés/seg (\(60\)mph) quando os freios são acionados. O carro começa a desacelerar a uma taxa constante de\(15\) pés/seg 2.
- Quantos segundos se passam antes que o carro pare?
- Até onde o carro viaja durante esse período?
Solução
a. Primeiro, introduzimos variáveis para esse problema. \(t\)Seja o tempo (em segundos) após a primeira aplicação dos freios. \(a(t)\)Seja a aceleração do carro (em pés por segundo quadrado) de cada vez\(t\). \(v(t)\)Seja a velocidade do carro (em pés por segundo) de cada vez\(t\). \(s(t)\)Seja a posição do carro (em pés) além do ponto em que os freios são acionados no momento\(t\).
O carro está viajando a uma taxa de\(88\) pés/seg. Portanto, a velocidade inicial é\(v(0)=88\) ft/seg. Como o carro está desacelerando, a aceleração é
\(a(t)=−15\,\text{ft/sec}^2\).
A aceleração é a derivada da velocidade,
\(v′(t)=-15.\)
Portanto, temos um problema de valor inicial para resolver:
\(v′(t)=−15,\quad v(0)=88.\)
Integrando, descobrimos que
\(v(t)=−15t+C.\)
Uma vez que\(v(0)=88,C=88.\) Assim, a função de velocidade é
\(v(t)=−15t+88.\)
Para descobrir quanto tempo leva para o carro parar, precisamos encontrar o tempo de\(t\) forma que a velocidade seja zero. Resolvendo\(−15t+88=0,\), obtemos\(t=\dfrac{88}{15}\) segundos.
b. Para descobrir até onde o carro viaja durante esse período, precisamos encontrar a posição do carro após um\(\dfrac{88}{15}\) segundo. Sabemos que a velocidade\(v(t)\) é a derivada da posição\(s(t)\). Considere a posição inicial como sendo\(s(0)=0\). Portanto, precisamos resolver o problema do valor inicial
\(s′(t)=−15t+88,\quad s(0)=0.\)
Integrando, temos
\(s(t)=−\dfrac{15}{2}t^2+88t+C.\)
Desde então\(s(0)=0\), a constante é\(C=0\). Portanto, a função de posição é
\(s(t)=−\dfrac{15}{2}t^2+88t.\)
Depois de um\(t=\frac{88}{15}\) segundo, a posição é\(s\left(\frac{88}{15}\right)≈258.133\) ft.
Suponha que o carro esteja viajando a uma taxa de\(44\) pés/seg. Quanto tempo leva para o carro parar? Até onde o carro vai viajar?
- Dica
-
\(v(t)=−15t+44.\)
- Responda
-
\(2.93\)seg,\(64.5\) pés
Conceitos chave
- Se\(F\) é uma antiderivada de\(f,\) então toda antiderivada de\(f\) é da forma\(F(x)+C\) de alguma constante\(C\).
- Resolver o problema do valor inicial\[\dfrac{dy}{dx}=f(x),\quad y(x_0)=y_0 \nonumber \] exige que primeiro encontremos o conjunto de antiderivadas de\(f\) e, em seguida, procuremos a antiderivada específica que também satisfaça a condição inicial.
Glossário
- antiderivado
- uma função\(F\) tal que\(F′(x)=f(x)\) para todos\(x\) no domínio de\(f\) é uma antiderivada de\(f\)
- integral indefinido
- a antiderivada mais geral de\(f(x)\) é a integral indefinida de\(f\); usamos a notação\(\displaystyle \int f(x)\,dx\) para denotar a integral indefinida de\(f\)
- problema de valor inicial
- um problema que requer encontrar uma função\(y\) que satisfaça a equação diferencial\(\dfrac{dy}{dx}=f(x)\) junto com a condição inicial\(y(x_0)=y_0\)


