4.9: Método de Newton

Objetivos de

• Descreva as etapas do método de Newton.
• Explique o que significa um processo iterativo.
• Reconheça quando o método de Newton não funciona.
• Aplique processos iterativos em várias situações.

Em muitas áreas da matemática pura e aplicada, estamos interessados em encontrar soluções para uma equação da forma.\(f(x)=0.\) Para a maioria das funções, no entanto, é difícil — se não impossível — calcular seus zeros explicitamente. Nesta seção, examinamos uma técnica que fornece uma maneira muito eficiente de aproximar os zeros das funções. Essa técnica faz uso de aproximações de linha tangente e está por trás do método usado frequentemente por calculadoras e computadores para encontrar zeros.

Descrevendo o método de Newton

Considere a tarefa de encontrar as soluções de\(f(x)=0.\) Se\(f\) for o polinômio de primeiro grau\(f(x)=ax+b\), então a solução de\(f(x)=0\) é dada pela fórmula\(x=−\frac{b}{a}\). Se\(f\) for o polinômio de segundo grau\(f(x)=ax^2+bx+c\), as soluções de\(f(x)=0\) podem ser encontradas usando a fórmula quadrática. No entanto, para polinômios de grau 3 ou mais, encontrar raízes de\(f\) se torna mais complicado. Embora existam fórmulas para polinômios de terceiro e quarto graus, elas são bastante complicadas. Além disso, se f for um polinômio de grau 5 ou maior, sabe-se que essas fórmulas não existem. Por exemplo, considere a função

\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]

Não existe uma fórmula que nos permita encontrar as soluções de Dificuldades\(f(x)=0.\) semelhantes para funções não polinomiais. Por exemplo, considere a tarefa de encontrar soluções de\(\tan(x)−x=0.\) Nenhuma fórmula simples existe para as soluções dessa equação. Em casos como esses, podemos usar o método de Newton para aproximar as raízes.

O método de Newton usa a seguinte ideia para aproximar as soluções de\(f(x)=0.\) Ao esboçar um gráfico de\(f\), podemos estimar uma raiz de\(f(x)=0\). Vamos chamar isso de estimativa\(x_0\). Em seguida, desenhamos a linha tangente a\(f\) at\(x_0\). Se\(f′(x_0)≠0\), essa linha tangente cruza o\(x\) eixo -em algum ponto\((x_1,0)\). Agora,\(x_1\) seja a próxima aproximação da raiz real. Normalmente,\(x_1\) está mais perto do\(x_0\) que de uma raiz real. Em seguida, desenhamos a linha tangente a\(f\) at\(x_1\). Se\(f′(x_1)≠0\), essa linha tangente também cruza o\(x\) eixo -, produzindo outra aproximação,\(x_2\). Continuamos dessa maneira, derivando uma lista de aproximações:\(x_0,\, x_1,\, x_2,\, ….\) Normalmente, os números se aproximam\(x_0,\, x_1,\, x_2,\, …\) rapidamente de uma raiz real\(x^*\), conforme mostrado na figura a seguir.

Figura: As\(\PageIndex{1}\) aproximações se aproximam\(x_0,\, x_1,\, x_2,\, … \) da raiz real.\(x^*\) As aproximações são derivadas observando as linhas tangentes ao gráfico de\(f\).

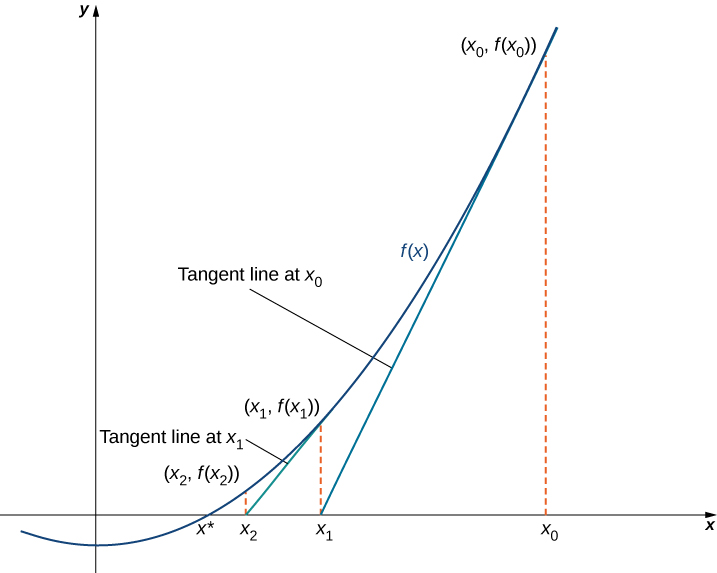
Agora vamos ver como calcular as aproximações\(x_0,\, x_1,\, x_2,\, ….\) Se\(x_0\) for nossa primeira aproximação, a aproximação\(x_1\) é definida deixando\((x_1,0)\) ser o\(x\) intercepto -da reta tangente a\(f\) at\(x_0\). A equação dessa reta tangente é dada por

\[y=f(x_0)+f′(x_0)(x−x_0). \nonumber \]

Portanto,\(x_1\) deve satisfazer

\[f(x_0)+f′(x_0)(x_1−x_0)=0.\nonumber \]

Resolvendo essa equação para\(x_1\), concluímos que

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}.\nonumber \]

Da mesma forma, o ponto\((x_2,0)\) é o\(x\) intercepto -da reta tangente a\(f\) at\(x_1\). Portanto,\(x_2\) satisfaz a equação

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}.\nonumber \]

Em geral, para\(n>0,x_n\) satisfazer

\[x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}.\label{Newton} \]

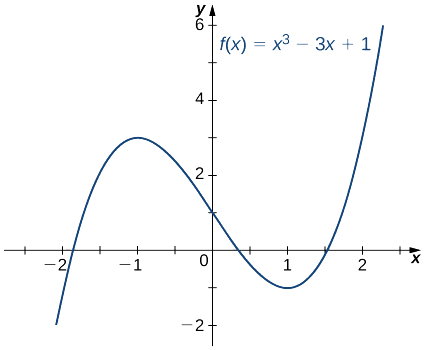
A seguir, vemos como fazer uso dessa técnica para aproximar a raiz do polinômio.\(f(x)=x^3−3x+1.\)

Exemplo\(\PageIndex{1}\): Finding a Root of a Polynomial

Use o método de Newton para aproximar uma raiz de\(f(x)=x^3−3x+1\) no intervalo\([1,2]\). Deixe\(x_0=2\)\(x_1,\, x_2, \,x_3, \,x_4,\) e encontre\(x_5\) e.

Solução

Na Figura\(\PageIndex{2}\), vemos que\(f\) tem uma raiz sobre o intervalo\([1,2]\). Portanto,\(x_0=2\) parece uma primeira aproximação razoável. Para encontrar a próxima aproximação, usamos Equation\ ref {Newton}. Desde então\(f(x)=x^3−3x+1\), a derivada é\(f′(x)=3x^2−3\). Usando a Equação\ ref {Newton} com\(n=1\) (e uma calculadora que exibe\(10\) dígitos), obtemos

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}=2−\frac{f(2)}{f'(2)}=2−\frac{3}{9}≈1.666666667.\nonumber \]

Para encontrar a próxima aproximação\(x_2\), usamos a Equação\ ref {Newton} com\(n=2\) e o valor de\(x_1\) armazenado na calculadora. Nós descobrimos que

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}≈1.548611111.\nonumber \]

Continuando dessa forma, obtemos os seguintes resultados:

• \(x_1≈1.666666667\)
• \(x_2≈1.548611111\)
• \(x_3≈1.532390162\)
• \(x_4≈1.532088989\)
• \(x_5≈1.532088886\)
• \(x_6≈1.532088886.\)

Observamos que obtivemos o mesmo valor para\(x_5\)\(x_6\) e. Portanto, qualquer aplicação subsequente do método de Newton provavelmente fornecerá o mesmo valor para\(x_n\).

Figura\(\PageIndex{2}\): A função\(f(x)=x^3−3x+1\) tem uma raiz sobre o intervalo\([1,2].\)

Exercício\(\PageIndex{1}\)

Vamos usar o método de Newton para aproximar a raiz do intervalo\(f(x)=x^3−3x+1\) ao longo do intervalo\([0,1]\) calculando\(x_1\)\(x_2\) e.\(x_0=0\)

Dica

Use a Equação\ ref {Newton}.

Responda

\(x_1≈0.33333333\)
\(x_2≈0.347222222\)

O método de Newton também pode ser usado para aproximar raízes quadradas. Aqui mostramos como aproximar\(\sqrt{2}\). Esse método pode ser modificado para aproximar a raiz quadrada de qualquer número positivo.

Exemplo\(\PageIndex{2}\): Finding a Square Root

Use o método de Newton para aproximar\(\sqrt{2}\) (Figura\(\PageIndex{3}\)). Deixe\(f(x)=x^2−2\)\(x_0=2\), deixe e calcule\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). (Observamos que, como\(f(x)=x^2−2\) tem um zero em\(\sqrt{2}\), o valor inicial\(x_0=2\) é uma opção razoável para aproximar\(\sqrt{2}\)).

Figura\(\PageIndex{3}\): Podemos usar o método de Newton para encontrar\(\sqrt{2}\).

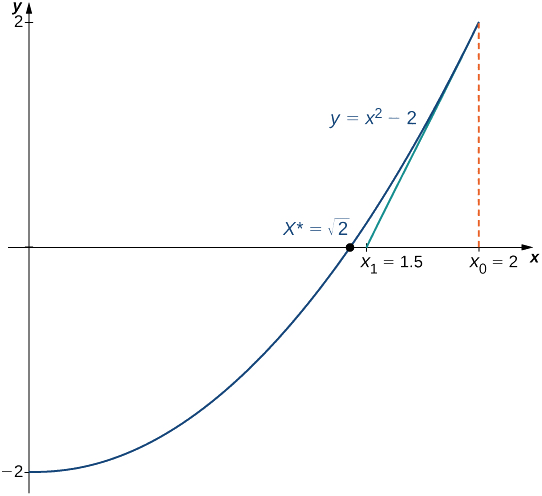
Solução

Para\(f(x)=x^2−2,\; f′(x)=2x.\) From Equation\ ref {Newton}, sabemos que

\ [\ begin {align*} x_n&=x_ {n−1} −\ frac {f (x_ {n−1})} {f' (x_ {n−1})}\\ [4pt]
&=x_ {n−1} −\ frac {x^2_ {n−1} −2} {2x_ {n−1}}\\ [4] pt]
&=\ frac {1} {2} x_ {n−1} +\ frac {1} {x_ {n−1}}\\ [4pt]
&=\ frac {1} {2}\ left (x_ {n−1} +\ frac {2} {x_ {n−1}}\ direita). \ end {align*}\ nonumber\]

Portanto,

\(x_1=\frac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\frac{1}{2}\left(2+\frac{2}{2}\right)=1.5\)

\(x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{1}{2}\left(1.5+\frac{2}{1.5}\right)≈1.416666667.\)

Continuando dessa maneira, descobrimos que

\(x_1=1.5\)

\(x_2≈1.416666667\)

\(x_3≈1.414215686\)

\(x_4≈1.414213562\)

\(x_5≈1.414213562.\)

Como obtivemos o mesmo valor para\(x_4\) e\(x_5\), é improvável que o valor\(x_n\) mude em qualquer aplicação subsequente do método de Newton. Concluímos que\(\sqrt{2}≈1.414213562.\)

Exercício\(\PageIndex{2}\)

Use o método de Newton para aproximar\(\sqrt{3}\) deixando\(f(x)=x^2−3\)\(x_0=3\) e. Encontre\(x_1\)\(x_2\) e.

Dica

Para\(f(x)=x^2−3\), a Equação\ ref {Newton} se reduz para\(x_n=\frac{x_{n−1}}{2}+\frac{3}{2x_{n−1}}\).

Responda

\(x_1=2\)
\(x_2=1.75\)

Ao usar o método de Newton, cada aproximação após a estimativa inicial é definida em termos da aproximação anterior usando a mesma fórmula. Em particular, definindo a função\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\), podemos reescrever Equation\ ref {Newton} como\(x_n=F(x_{n−1})\). Esse tipo de processo, em que cada um\(x_n\) é definido em termos\(x_{n−1}\) de repetição da mesma função, é um exemplo de processo iterativo. Em breve, examinaremos outros processos iterativos. Primeiro, vamos ver as razões pelas quais o método de Newton pode falhar em encontrar uma raiz.

Falhas do método de Newton

Normalmente, o método de Newton é usado para encontrar raízes com bastante rapidez. No entanto, as coisas podem dar errado. Alguns motivos pelos quais o método de Newton pode falhar incluem o seguinte:

1. Em uma das aproximações\(x_n\), a derivada\(f′\) é zero em\(x_n\), mas\(f(x_n)≠0\). Como resultado, a linha tangente de\(f\) at\(x_n\) não cruza o\(x\) eixo y. Portanto, não podemos continuar o processo iterativo.
2. As aproximações\(x_0,\, x_1,\, x_2,\, …\) podem se aproximar de uma raiz diferente. Se a função\(f\) tiver mais de uma raiz, é possível que nossas aproximações não se aproximem daquela que estamos procurando, mas se aproximem de uma raiz diferente (veja a Figura\(\PageIndex{4}\)). Esse evento ocorre com mais frequência quando não escolhemos a aproximação\(x_0\) próxima o suficiente da raiz desejada.
3. As aproximações podem falhar em se aproximar completamente de uma raiz. No exemplo\(\PageIndex{3}\), fornecemos um exemplo de uma função e uma estimativa inicial de\(x_0\) forma que as aproximações sucessivas nunca se aproximem de uma raiz porque as aproximações sucessivas continuam alternando entre dois valores.

Figura\(\PageIndex{4}\): Se a estimativa inicial\(x_0\) estiver muito longe da raiz procurada, isso pode levar a aproximações que se aproximam de uma raiz diferente.

Exemplo\(\PageIndex{3}\): When Newton’s Method Fails

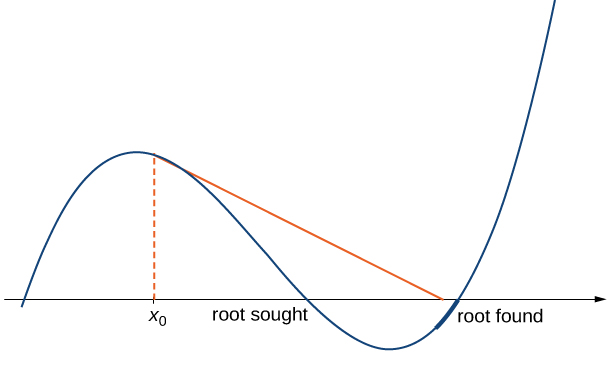
Considere a função\(f(x)=x^3−2x+2\). Deixe\(x_0=0\). Mostre que a sequência\(x_1,\, x_2,\, …\) não consegue se aproximar de uma raiz de\(f\).

Solução

Pois\(f(x)=x^3−2x+2,\) a derivada é\(f′(x)=3x^2−2\) .Portanto,

\[x_1=x_0−\frac{f(x_0)}{f′(x_0)}=0−\frac{f(0)}{f′(0)}=−\frac{2}{−2}=1. \nonumber \]

Na próxima etapa,

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}=1−\frac{f(1)}{f′(1)}=1−\frac{1}{1}=0. \nonumber \]

Consequentemente, os números\(x_0,\, x_1,\, x_2,\, …\) continuam saltando para frente\(0\) e para trás\(1\) e nunca se aproximam da raiz dos\(f\) quais está acima do intervalo\([−2,−1]\) (Figura\(\PageIndex{5}\)). Felizmente, se escolhermos uma\(x_0\) aproximação inicial mais próxima da raiz real, poderemos evitar essa situação.

Figura\(\PageIndex{5}\): As aproximações continuam alternando entre\(0\)\(1\) e nunca se aproximando da raiz de\(f\).

Exercício\(\PageIndex{3}\)

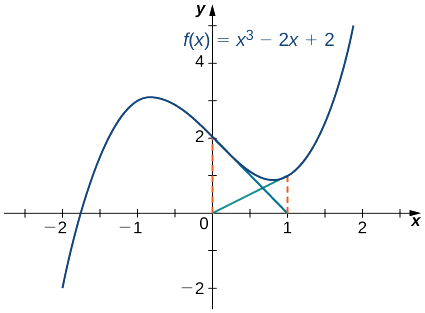
Para\(f(x)=x^3−2x+2,\) deixar\(x_0=−1.5\)\(x_1\) e encontrar\(x_2\) e.

Dica

Use a Equação\ ref {Newton}.

Responda

\(x_1≈−1.842105263\)
\(x_2≈−1.772826920\)

\(\PageIndex{3}\)Em Example, vemos que o método de Newton nem sempre funciona. No entanto, quando funciona, a sequência de aproximações se aproxima da raiz muito rapidamente. Discussões sobre a rapidez com que a sequência de aproximações se aproxima de uma raiz encontrada usando o método de Newton estão incluídas em textos sobre análise numérica.

Outros processos iterativos

Como mencionado anteriormente, o método de Newton é um tipo de processo iterativo. Agora, veremos um exemplo de um tipo diferente de processo iterativo.

Considere uma função\(F\) e um número inicial\(x_0\). Defina os números subsequentes\(x_n\) pela fórmula\(x_n=F(x_{n−1})\). Esse processo é um processo iterativo que cria uma lista de números.\(x_0,\, x_1,\, x_2,\, …,\, x_n,\, ….\) Essa lista de números pode\(n\) se aproximar de um número finito\(x^*\) à medida que aumenta, ou pode não. Em Exemplo\(\PageIndex{4}\), vemos um exemplo de uma função\(F\) e uma estimativa inicial de\(x_0\) forma que a lista resultante de números se aproxime de um valor finito.

Exemplo\(\PageIndex{4}\): Finding a Limit for an Iterative Process

Deixe\(F(x)=\frac{1}{2}x+4\) e deixe\(x_0=0\). Para todos\(n≥1\), deixe\(x_n=F(x_{n−1})\). Encontre os valores\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Faça uma conjectura sobre o que acontece com essa lista de números\(x_1,\, x_2,\, x_3,\, …,\, x_n,\, …\) como\(n→∞\). Se a lista de números se\(x_1,\, x_2,\, x_3,\, …\) aproximar de um número finito\(x^*\), então\(x^*\) satisfaz\(x^*=F(x^*)\) e\(x^*\) é chamada de ponto fixo de\(F\).

Solução

Se\(x_0=0\), então

• \(x_1=\frac{1}{2}(0)+4=4\)
• \(x_2=\frac{1}{2}(4)+4=6\)
• \(x_3=\frac{1}{2}(6)+4=7\)
• \(x_4=\frac{1}{2}(7)+4=7.5\)
• \(x_5=\frac{1}{2}(7.5)+4=7.75\)
• \(x_6=\frac{1}{2}(7.75)+4=7.875\)
• \(x_7=\frac{1}{2}(7.875)+4=7.9375\)
• \(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
• \(x _9=\frac{1}{2}(7.96875)+4=7.984375.\)

A partir dessa lista, conjecturamos que os valores se\(x_n\) aproximam\(8\).

\(\PageIndex{6}\)A figura fornece um argumento gráfico de que os valores se aproximam\(8\) como\(n→∞\). Começando no ponto\((x_0,x_0)\), desenhamos uma linha vertical até o ponto\((x_0,F(x_0))\). O próximo número em nossa lista é\(x_1=F(x_0)\). Usamos\(x_1\) para calcular\(x_2\). Portanto, desenhamos uma linha horizontal conectando-se\((x_0,x_1)\) ao ponto\((x_1,x_1)\) na linha e\(y=x\), em seguida, desenhamos uma linha vertical conectando-se\((x_1,x_1)\) ao ponto\((x_1,F(x_1))\). A saída\(F(x_1)\) se torna\(x_2\). Continuando dessa forma, poderíamos criar um número infinito de segmentos de linha. Esses segmentos de linha estão presos entre as linhas\(F(x)=\frac{x}{2}+4\)\(y=x\) e. Os segmentos de linha se aproximam do ponto de interseção dessas duas linhas, o que ocorre quando\(x=F(x)\). Resolvendo a equação,\(x=\frac{x}{2}+4,\) concluímos que eles se cruzam em\(x=8\). Portanto, nossa evidência gráfica concorda com nossa evidência numérica de que a lista de números\(x_0,\, x_1,\, x_2,\, …\) se aproxima\(x^*=8\) como\(n→∞\).

Figura\(\PageIndex{6}\): Esse processo iterativo aborda o valor\(x^*=8.\)

Exercício\(\PageIndex{4}\)

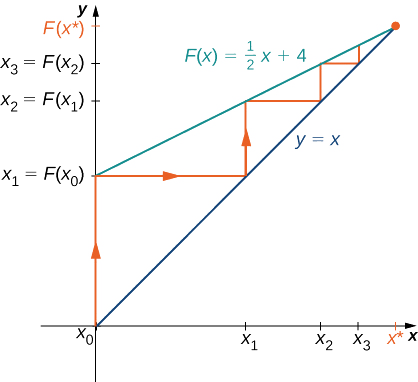
Considere a função\(F(x)=\frac{1}{3}x+6\). Deixe\(x_0=0\) e deixe\(x_n=F(x_{n−1})\) para\(n≥2\). Encontre\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Faça uma conjectura sobre o que acontece com a lista de números\(x_1,\, x_2,\, x_3,\, …\, x_n,\, … \) como\(n→∞.\)

Dica

Considere o ponto em que\(y=x\) as linhas\(y=F(x)\) se cruzam.

Responda

\(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)

Processos iterativos e caos

Processos iterativos podem produzir um comportamento muito interessante. Nesta seção, vimos vários exemplos de processos iterativos que convergem para um ponto fixo. Também vimos no Exemplo\(\PageIndex{3}\) que o processo iterativo saltou para frente e para trás entre dois valores. Chamamos esse tipo de comportamento de 2 ciclos. Os processos iterativos podem convergir para ciclos com várias periodicidades, como 2 ciclos, 4 ciclos (em que o processo iterativo repete uma sequência de quatro valores), 8 ciclos e assim por diante.

Alguns processos iterativos produzem o que os matemáticos chamam de caos. Nesse caso, o processo iterativo salta de valor para valor de uma forma aparentemente aleatória e nunca converge ou se estabelece em um ciclo. Embora uma exploração completa do caos esteja além do escopo deste texto, neste projeto, examinamos uma das principais propriedades de um processo iterativo caótico: dependência sensível das condições iniciais. Essa propriedade se refere ao conceito de que pequenas mudanças nas condições iniciais podem gerar um comportamento drasticamente diferente no processo iterativo.

Provavelmente, o exemplo mais conhecido de caos é o conjunto Mandelbrot (veja a Figura\(\PageIndex{7}\)), em homenagem a Benoit Mandelbrot (1924—2010), que investigou suas propriedades e ajudou a popularizar o campo da teoria do caos. O conjunto Mandelbrot geralmente é gerado por computador e mostra detalhes fascinantes sobre a ampliação, incluindo a autorreplicação do conjunto. Várias versões coloridas do conjunto foram exibidas em museus e podem ser encontradas on-line e em livros populares sobre o assunto.

Figura\(\PageIndex{7}\): O conjunto de Mandelbrot é um exemplo bem conhecido de um conjunto de pontos gerados pelo comportamento caótico iterativo de uma função relativamente simples.

Neste projeto, usamos o mapa logístico

\[f(x)=rx(1−x) \nonumber \]

onde\(x∈[0,1]\) e\(r>0\)

como a função em nosso processo iterativo. O mapa logístico é uma função aparentemente simples; mas, dependendo do valor de\(r\), o processo iterativo resultante exibe um comportamento muito interessante. Isso pode levar a pontos fixos, ciclos e até mesmo caos.

Para visualizar o comportamento de longo prazo do processo iterativo associado ao mapa logístico, usaremos uma ferramenta chamada diagrama de teia de aranha. Como fizemos com o processo iterativo que examinamos anteriormente nesta seção, primeiro desenhamos uma linha vertical do ponto\((x_0,0)\) ao ponto\((x_0,f(x_0))=(x_0,x_1)\). Em seguida, desenhamos uma linha horizontal desse ponto a ponto\((x_1,f(x_1))=(x_1,x_2)\),\((x_1,x_1),\) depois desenhamos uma linha vertical e continuamos o processo até que o comportamento de longo prazo do sistema se torne aparente. A figura\(\PageIndex{8}\) mostra o comportamento de longo prazo do mapa logístico quando\(r=3.55\)\(x_0=0.2\) e. (As primeiras\(100\) iterações não são plotadas.) O comportamento de longo prazo desse processo iterativo é um\(8\) ciclo.

Figura\(\PageIndex{8}\): Um diagrama de teia de aranha para\(f(x)=3.55x(1−x)\) é apresentado aqui. A sequência de valores resulta em um ciclo de 8.

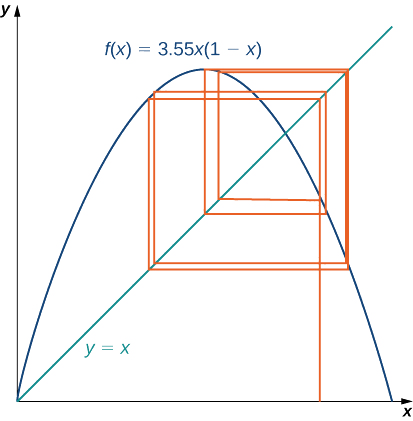
1. Deixe\(r=0.5\) e escolha\(x_0=0.2\). Manualmente ou usando um computador, calcule os primeiros\(10\) valores na sequência. A sequência parece convergir? Em caso afirmativo, até que valor? Isso resulta em um ciclo? Em caso afirmativo, que tipo de ciclo (por exemplo,\(2\) −ciclo,\(4\) −ciclo.)?
2. O que acontece quando\(r=2\)?
3. Para\(r=3.2\) e\(r=3.5\), calcule os primeiros valores da\(100\) sequência. Gere um diagrama de teia de aranha para cada processo iterativo. (Vários applets gratuitos estão disponíveis on-line que geram diagramas de teia de aranha para o mapa logístico.) Qual é o comportamento de longo prazo em cada um desses casos?
4. Agora vamos\(r=4.\) calcular os primeiros valores da\(100\) sequência e gerar um diagrama de teia de aranha. Qual é o comportamento de longo prazo nesse caso?
5. Repita o processo para\(r=4,\), mas deixe.\(x_0=0.201.\) Como esse comportamento se compara ao comportamento de\(x_0=0.2\)?

Conceitos-chave

• O método de Newton aproxima as raízes\(f(x)=0\) de começando com uma aproximação inicial e\(x_0\), em seguida, usa linhas tangentes ao gráfico de\(f\) para criar uma sequência de aproximações\(x_1,\, x_2,\, x_3,\, ….\)
• Normalmente, o método de Newton é um método eficiente para encontrar uma raiz específica. Em certos casos, o método de Newton não funciona porque a lista de números\(x_0,\, x_1,\, x_2,\, …\) não se aproxima de um valor finito ou se aproxima de um valor diferente da raiz procurada.
• Qualquer processo no qual uma lista de números\(x_0,\, x_1,\, x_2,\, …\) é gerada definindo um número inicial\(x_0\) e definindo os números subsequentes pela equação\(x_n=F(x_{n−1})\) para alguma função\(F\) é um processo iterativo. O método de Newton é um exemplo de um processo iterativo, onde a função\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\) para uma determinada função\(f\).

Glossário

processo iterativo

processo no qual uma lista de números\(x_0,x_1,x_2,x_3…\) é gerada iniciando com um número\(x_0\) e definindo\(x_n=F(x_{n−1})\) para\(n≥1\)

Método de Newton

método para aproximar as raízes do\(f(x)=0;\) uso de uma estimativa inicial\(x_0\); cada aproximação subsequente é definida pela equação\(x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}\)