4.8: Regra do L'Hôpital

Objetivos de

• Reconheça quando aplicar a regra do L'Hôpital.
• Identifique formas indeterminadas produzidas por quocientes, produtos, subtrações e potências e aplique a regra de L'Hôpital em cada caso.
• Descreva as taxas de crescimento relativas das funções.

Nesta seção, examinamos uma ferramenta poderosa para avaliar limites. Essa ferramenta, conhecida como regra de L'Hôpital, usa derivadas para calcular limites. Com essa regra, poderemos avaliar muitos limites que ainda não conseguimos determinar. Em vez de confiar em evidências numéricas para conjecturar que existe um limite, poderemos mostrar definitivamente que existe um limite e determinar seu valor exato.

Aplicando a regra do L'Hôpital

A regra de L'Hôpital pode ser usada para avaliar limites envolvendo o quociente de duas funções. Considere

\[\lim_{x→a}\dfrac{f(x)}{g(x)}. \nonumber \]

Se\(\displaystyle \lim_{x→a}f(x)=L_1\) e\(\displaystyle \lim_{x→a}g(x)=L_2≠0,\) depois

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}. \nonumber \]

No entanto, o que acontece se\(\displaystyle \lim_{x→a}f(x)=0\) e\(\displaystyle \lim_{x→a}g(x)=0\)? Chamamos isso de uma das formas indeterminadas, do tipo\(\dfrac{0}{0}\). Isso é considerado uma forma indeterminada porque não podemos determinar o comportamento exato de\(\dfrac{f(x)}{g(x)}\) as\(x→a\) sem uma análise mais aprofundada. Vimos exemplos disso anteriormente no texto. Por exemplo, considere

\[\lim_{x→2}\dfrac{x^2−4}{x−2} \nonumber \]

e

\[\lim_{x→0}\dfrac{\sin x}{x}.\nonumber \]

Para o primeiro desses exemplos, podemos calcular o limite fatorando o numerador e escrevendo

\[\lim_{x→2}\dfrac{x^2−4}{x−2}=\lim_{x→2}\dfrac{(x+2)(x−2)}{x−2}=\lim_{x→2}(x+2)=2+2=4. \nonumber \]

\(\displaystyle \lim_{x→0}\dfrac{\sin x}{x}\)Pois conseguimos mostrar, usando um argumento geométrico, que

\[\lim_{x→0}\dfrac{\sin x}{x}=1. \nonumber \]

Aqui, usamos uma técnica diferente para avaliar limites como esses. Essa técnica não apenas fornece uma maneira mais fácil de avaliar esses limites, mas também, e mais importante, ela nos fornece uma maneira de avaliar muitos outros limites que não podíamos calcular anteriormente.

A ideia por trás da regra de L'Hôpital pode ser explicada usando aproximações lineares locais. Considere duas funções diferenciáveis\(f\) e de\(g\) tal forma que,\(g′(a)≠0\) de\(x\) perto\(a\), possamos escrever\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\)

\[f(x)≈f(a)+f′(a)(x−a) \nonumber \]

e

\[g(x)≈g(a)+g′(a)(x−a). \nonumber \]

Portanto,

\[\dfrac{f(x)}{g(x)}≈\dfrac{f(a)+f′(a)(x−a)}{g(a)+g′(a)(x−a)}. \nonumber \]

Figura\(\PageIndex{1}\): Se\(\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x)\), então a razão\(f(x)/g(x)\) é aproximadamente igual à razão de suas aproximações lineares próximas\(a\).

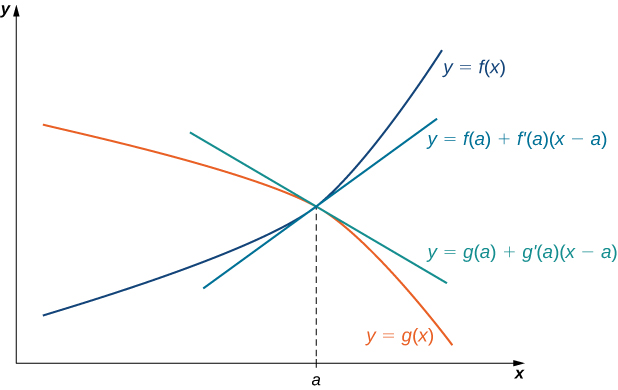
Uma vez que\(f\) é diferenciável em\(a\), então\(f\) é contínuo em\(a\), e portanto\(\displaystyle f(a)=\lim_{x→a}f(x)=0\). Da mesma forma,\(\displaystyle g(a)=\lim_{x→a}g(x)=0\). Se também assumirmos isso\(f′\) e\(g′\) formos contínuos em\(x=a\), então\(\displaystyle f′(a)=\lim_{x→a}f′(x)\)\(\displaystyle g′(a)=\lim_{x→a}g′(x)\) e. Usando essas ideias, concluímos que

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)(x−a)}{g′(x)(x−a)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} . \nonumber \]

Observe que a suposição de que\(f′\) e\(g′\) são contínuos\(a\) e\(g′(a)≠0\) podem ser afrouxados. Declaramos formalmente a regra de L'Hôpital para a forma indeterminada\(\dfrac{0}{0}\). Observe também que a notação não\(\dfrac{0}{0}\) significa que estamos realmente dividindo zero por zero. Em vez disso, estamos usando a notação\(\dfrac{0}{0}\) para representar um quociente de limites, cada um dos quais é zero.

Regra de L'Hôpital (Caso 0/0)

Suponha\(f\) e\(g\) sejam funções diferenciáveis em um intervalo aberto contendo\(a\), exceto possivelmente em\(a\). Se\(\displaystyle \lim_{x→a}f(x)=0\) e\(\displaystyle \lim_{x→a}g(x)=0,\) depois

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, \nonumber \]

assumindo que o limite à direita existe ou é\(∞\) ou\(−∞\). Esse resultado também se aplica se estivermos considerando limites unilaterais, ou se\(a=∞\) ou\(a=−∞.\)

Prova

Nós fornecemos uma prova desse teorema no caso especial quando\(f,g,f′,\) e\(g′\) são todos contínuos em um intervalo aberto contendo\(a\). Nesse caso, uma vez que\(\displaystyle\lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) e\(f\) e\(g\) são contínuos em\(a\), segue isso\(f(a)=0=g(a)\). Portanto,

\ [\ begin {align*}\ lim_ {x→a}\ dfrac {f (x)} {g (x)} &=\ lim_ {x→a}\ dfrac {f (x) −f (a)} {g (x) −g (a)} & &\ texto {Desde}\, f (a) =0=g (a)\\ [4pt]
=\ lim_ {x→a}\ dfrac {\ dfrac {f (x) −f (a)} {x−a}} {\ dfrac {g (x) −g (a)} {x−a}} & &\ text {Multiplique o numerador e o denominador por}\,\ frac {1} {x-a}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→a}\ dfrac {f (x) −f (a)} {x−a}} {\ displaystyle\ lim_ {x→a}\ dfrac {g (x) −g (a)} {x−a}} & &\ text {O limite de um quociente é o quociente dos limites}.\\ [4pt]
&=\ dfrac {f′( a)} {g′( a)} & &\ text {Pela definição da derivada}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→a} f′( x)} {\ displaystyle\ lim_ {x→a} g′( x)} & &\ text {Pela continuidade de}\, f′\,\ text {e}\, g′\\ [4pt]
&=\ lim_ {x→a}\ dfrac {f′x (x)} {g (x)}. & &\ text {O limite de um quociente}\ end {align*}\]

Observe que a regra de L'Hôpital afirma que podemos calcular o limite de um\(\dfrac{f}{g}\) quociente considerando o limite do quociente das derivadas\(\dfrac{f′}{g′}\). É importante perceber que não estamos calculando a derivada do quociente\(\dfrac{f}{g}\).

□

Exemplo\(\PageIndex{1}\): Applying L’Hôpital’s Rule (0/0 Case)

Avalie cada um dos seguintes limites aplicando a regra de L'Hôpital.

1. \(\displaystyle \lim_{x→0}\dfrac{1−\cos x}{x}\)
2. \(\displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}\)
3. \(\displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}\)
4. \(\displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}\)

Solução

a. Como o numerador\(1−\cos x→0\) e o denominador\(x→0\), podemos aplicar a regra de L'Hôpital para calcular esse limite. Nós temos

\[\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber \]

b. Como\(x→1,\) numerador\(\sin(πx)→0\) e denominador\(\ln(x)→0.\) Portanto, podemos aplicar a regra de L'Hôpital. Nós obtemos

\[\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber \]

c. Como\(x→∞\), o numerador\(e^{1/x}−1→0\) e o denominador\(\frac{1}{x}→0\). Portanto, podemos aplicar a regra de L'Hôpital. Nós obtemos

\[\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber \]

d. Quando o numerador\(x→0,\) e o denominador se aproximam de zero. Portanto, podemos aplicar a regra de L'Hôpital. Nós obtemos

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber \]

Como o numerador e o denominador desse novo quociente se aproximam tanto de zero quanto\(x→0\), aplicamos a regra de L'Hôpital novamente. Ao fazer isso, vemos que

\[\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber \]

Portanto, concluímos que

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber \]

Exercício\(\PageIndex{1}\)

Avalie\[\lim_{x→0}\dfrac{x}{\tan x}. \nonumber \]

Dica

\(\dfrac{d}{dx}\big(\tan x\big)=\sec^2x\)

Resposta

\(1\)

Também podemos usar a regra de L'Hôpital para avaliar os limites dos quocientes\(\dfrac{f(x)}{g(x)}\) nos quais\(f(x)→±∞\)\(g(x)→±∞\) e. Os limites dessa forma são classificados como formas indeterminadas do tipo\(∞/∞\). Novamente, observe que não estamos realmente dividindo\(∞\) por\(∞\). Como não\(∞\) é um número real, isso é impossível; ao contrário,\(∞/∞\) é usado para representar um quociente de limites, cada um dos quais é\(∞\) ou\(−∞\).

Regra de L'Hôpital (\(∞/∞\) Case)

Suponha\(f\) e\(g\) sejam funções diferenciáveis em um intervalo aberto contendo\(a\), exceto possivelmente em\(a\). Suponha\(\displaystyle\lim_{x→a}f(x)=∞\) (ou\(−∞\)) e\(\displaystyle\lim_{x→a}g(x)=∞\) (ou\(−∞\)). Então,

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber \]

assumindo que o limite à direita existe ou é\(∞\) ou\(−∞\). Esse resultado também é válido se o limite for infinito\(−∞\), se\(a=∞\) ou ou o limite for unilateral.

Exemplo\(\PageIndex{2}\): Applying L’Hôpital’s Rule (\(∞/∞\)) Case

Avalie cada um dos seguintes limites aplicando a regra de L'Hôpital.

1. \(\displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}\)
2. \(\displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}\)

Solução

a. Desde\(3x+5\) and \(2x+1\) are first-degree polynomials with positive leading coefficients, \(\displaystyle\lim_{x→∞}(3x+5)=∞\) and \(\displaystyle\lim_{x→∞}(2x+1)=∞\). Therefore, we apply L’Hôpital’s rule and obtain

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber \]

Observe que esse limite também pode ser calculado sem invocar a regra de L'Hôpital. No início do capítulo, mostramos como calcular esse limite dividindo o numerador e o denominador pela maior potência de x no denominador. Ao fazer isso, vimos que

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber \]

A regra de L'Hôpital nos fornece um meio alternativo de avaliar esse tipo de limite.

b. Aqui,\(\displaystyle \lim_{x→0^+}\ln x=−∞\)\(\displaystyle \lim_{x→0^+}\cot x=∞\) e. Portanto, podemos aplicar a regra de L'Hôpital e obter

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber \]

Agora como\(x→0^+, \csc^2x→∞\). Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \(\csc x\) to write

\[\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber \]

Agora\(\displaystyle\lim_{x→0^+}\sin^2x=0\) and \(\displaystyle\lim_{x→0^+}-x=0\), so we apply L’Hôpital’s rule again. We find

\[\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber \]

Concluímos que

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber \]

Exercício\(\PageIndex{2}\)

Avalie\[\lim_{x→∞}\dfrac{\ln x}{5x}. \nonumber \]

Dica

\(\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}\)

Resposta

\(0\)

Conforme mencionado, a regra de L'Hôpital é uma ferramenta extremamente útil para avaliar limites. É importante lembrar, no entanto, que aplicar a regra de L'Hôpital a um quociente\(\dfrac{f(x)}{g(x)}\), it is essential that the limit of \(\dfrac{f(x)}{g(x)}\) be of the form \(\dfrac{0}{0}\) or \(∞/∞\). Consider the following example.

Exemplo\(\PageIndex{3}\): When L’Hôpital’s Rule Does Not Apply

Considere\(\displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.\)

Mostre que o limite não pode ser avaliado aplicando a regra da L'Hôpital.

Solução

Como os limites do numerador e do denominador não são ambos zero nem infinitos, não podemos aplicar a regra de L'Hôpital. Se tentarmos fazer isso, obtemos

\[\dfrac{d}{dx}(x^2+5)=2x\nonumber \]

e

\[\dfrac{d}{dx}(3x+4)=3. \nonumber \]

Nesse ponto, concluiríamos erroneamente que

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber \]

No entanto, desde\(\displaystyle \lim_{x→1}(x^2+5)=6\) e\(\displaystyle \lim_{x→1}(3x+4)=7,\) nós realmente temos

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber \]

Podemos concluir que

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber \]

Exercício\(\PageIndex{3}\)

Explique por que não podemos aplicar a regra da L'Hôpital para avaliar\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\). Avalie\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\) por outros meios.

Dica

Determine os limites do numerador e do denominador separadamente.

Resposta

\(\displaystyle\lim_{x→0^+}\cos x=1.\)Portanto, não podemos aplicar a regra de L'Hôpital. O limite do quociente é\(∞.\)

Outras formas indeterminadas

A regra de L'Hôpital é muito útil para avaliar limites envolvendo as formas indeterminadas\(\dfrac{0}{0}\)\(∞/∞\) e. No entanto, também podemos usar a regra de L'Hôpital para ajudar a avaliar limites envolvendo outras formas indeterminadas que surgem ao avaliar limites. As expressões\(0⋅∞, ∞−∞, 1^∞, ∞^0\), e\(0^0\) são todas consideradas formas indeterminadas. Essas expressões não são números reais. Em vez disso, eles representam formas que surgem ao tentar avaliar certos limites. Em seguida, percebemos por que essas são formas indeterminadas e, em seguida, entendemos como usar a regra de L'Hôpital nesses casos. A ideia principal é que devemos reescrever as formas indeterminadas de forma que cheguemos à forma indeterminada\(\dfrac{0}{0}\) ou\(∞/∞\).

Forma indeterminada do tipo 0⋅∞

Suponha que queiramos avaliar\(\displaystyle \lim_{x→a}(f(x)⋅g(x))\), onde\(f(x)→0\) e\(g(x)→∞\) (ou\(−∞\)) como\(x→a\). Como um termo no produto está se aproximando de zero, mas o outro termo está se tornando arbitrariamente grande (em magnitude), tudo pode acontecer com o produto. Usamos a notação\(0⋅∞\) para indicar a forma que surge nessa situação. A expressão\(0⋅∞\) é considerada indeterminada porque não podemos determinar sem análises adicionais o comportamento exato do produto\(f(x)g(x)\) como\(x→∞\). Por exemplo,\(n\) seja um número inteiro positivo e considere

\(f(x)=\dfrac{1}{(x^n+1)}\)\(g(x)=3x^2\)e.

Como\(x→∞, f(x)→0\)\(g(x)→∞\) e. No entanto, o limite a partir\(x→∞\) de\(f(x)g(x)=\dfrac{3x^2}{(x^n+1)}\) varia, dependendo de\(n\). Se\(n=2\), então\(\displaystyle\lim_{x→∞}f(x)g(x)=3\). Se\(n=1\), então\(\displaystyle\lim_{x→∞}f(x)g(x)=∞\). Se\(n=3\), então\(\displaystyle\lim_{x→∞}f(x)g(x)=0\). Aqui, consideramos outro limite envolvendo a forma indeterminada\(0⋅∞\) e mostramos como reescrever a função como um quociente para usar a regra de L'Hôpital.

Exemplo\(\PageIndex{4}\): Indeterminate Form of Type \(0⋅∞\)

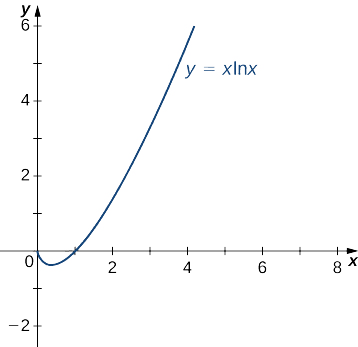
Avalie\(\displaystyle \lim_{x→0^+}x\ln x.\)

Solução

Primeiro, reescreva a função\(x\ln x\) como um quociente para aplicar a regra de L'Hôpital. Se escrevermos

\[x\ln x=\dfrac{\ln x}{1/x} \nonumber \]

vemos isso\(\ln x→−∞\) como\(x→0^+\) e\(\dfrac{1}{x}→∞\) como\(x→0^+\). Portanto, podemos aplicar a regra de L'Hôpital e obter

\[\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber \]

Concluímos que

\[\lim_{x→0^+}x\ln x=0. \nonumber \]

Figura\(\PageIndex{2}\): Encontrando o limite em\(x=0\) da função\(f(x)=x\ln x.\)

Exercício\(\PageIndex{4}\)

Avalie\[\lim_{x→0}x\cot x. \nonumber \]

Dica

Escreva\(x\cot x=\dfrac{x \cos x}{\sin x}\)

Resposta

\(1\)

Forma indeterminada do tipo\(∞−∞\)

Outro tipo de forma indeterminada é\(∞−∞.\) Considere o exemplo a seguir. \(n\)Seja um número inteiro positivo\(f(x)=3x^n\) e deixe\(g(x)=3x^2+5\) e. Como\(x→∞, f(x)→∞\)\(g(x)→∞\) e. Estamos interessados em\(\displaystyle\lim_{x→∞}(f(x)−g(x))\). Dependendo se\(f(x)\) cresce mais rápido,\(g(x)\) cresce mais rápido ou se eles crescem na mesma taxa, como vemos a seguir, tudo pode acontecer nesse limite. Desde\(f(x)→∞\) e\(g(x)→∞\), escrevemos\(∞−∞\) para denotar a forma desse limite. Como acontece com nossas outras formas indeterminadas, não\(∞−∞\) tem significado por si só e devemos fazer mais análises para determinar o valor do limite. Por exemplo, suponha que o expoente n na função\(f(x)=3x^n\) seja\(n=3\), então

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber \]

Por outro lado, se\(n=2,\) então

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber \]

No entanto, se\(n=1\), então

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber \]

Portanto, o limite não pode ser determinado considerando apenas\(∞−∞\). A seguir, veremos como reescrever uma expressão envolvendo a forma indeterminada\(∞−∞\) como uma fração para aplicar a regra de L'Hôpital.

Exemplo\(\PageIndex{5}\): Indeterminate Form of Type \(∞−∞\)

Avalie\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right). \nonumber \]

Solução

Ao combinar as frações, podemos escrever a função como um quociente. Uma vez que o denominador menos comum é que\(x^2\tan x,\) temos

\(\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}\).

Como\(x→0^+\), o numerador\(\tan x−x^2→0\) e o denominador\(x^2\tan x→0.\) Portanto, podemos aplicar a regra de L'Hôpital. Tomando as derivadas do numerador e do denominador, temos

\[\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber \]

Como\(x→0^+\),\((\sec^2x)−2x→1\)\(x^2\sec^2x+2x\tan x→0\) e. Como o denominador é positivo quando\(x\) se aproxima de zero da direita, concluímos que

\[\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber \]

Portanto,

\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber \]

Exercício\(\PageIndex{5}\)

Avalie\(\displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right)\).

Dica

Reescreva a diferença de frações como uma única fração.

Resposta

0

Outro tipo de forma indeterminada que surge ao avaliar limites envolve expoentes. As expressões\(0^0, ∞^0\), e\(1^∞\) são todas formas indeterminadas. Sozinhas, essas expressões não têm sentido porque não podemos realmente avaliá-las como avaliaríamos uma expressão envolvendo números reais. Em vez disso, essas expressões representam formas que surgem ao encontrar limites. Agora, examinamos como a regra de L'Hôpital pode ser usada para avaliar limites envolvendo essas formas indeterminadas.

Como a regra de L'Hôpital se aplica aos quocientes, usamos a função de logaritmo natural e suas propriedades para reduzir um problema avaliando um limite envolvendo expoentes a um problema relacionado envolvendo um limite de um quociente. Por exemplo, suponha que desejemos avaliar\(\displaystyle \lim_{x→a}f(x)^{g(x)}\) e cheguemos à forma indeterminada\(∞^0\). (As formas\(0^0\) indeterminadas\(1^∞\) podem ser tratadas de forma semelhante.) Procedemos da seguinte forma. Deixe

\[y=f(x)^{g(x)}. \nonumber \]

Então,

\[\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber \]

Portanto,

\[\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber \]

Já\(\displaystyle \lim_{x→a}f(x)=∞,\) que sabemos disso\(\displaystyle \lim_{x→a}\ln(f(x))=∞\). Portanto,\(\displaystyle \lim_{x→a}g(x)\ln(f(x))\) é de forma indeterminada\(0⋅∞\), e podemos usar as técnicas discutidas anteriormente para reescrever a expressão\(g(x)\ln(f(x))\) em uma forma para que possamos aplicar a regra de L'Hôpital. Suponha\(\displaystyle \lim_{x→a}g(x)\ln(f(x))=L\), onde\(L\) possa estar\(∞\) ou\(−∞.\) Então

\[\lim_{x→a}[\ln(y)]=L. \nonumber \]

Como a função logarítmica natural é contínua, concluímos que

\[\ln\left(\lim_{x→a}y\right)=L, \nonumber \]

o que nos dá

\[\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber \]

Exemplo\(\PageIndex{6}\): Indeterminate Form of Type \(∞^0\)

Avalie\[\lim_{x→∞}x^{1/x}. \nonumber \]

Solução

Deixe\(y=x^{1/x}\). Então,

\[\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber \]

Precisamos avaliar\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x}\). Aplicando a regra de L'Hôpital, obtemos

\[\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber \]

Portanto,\(\displaystyle \lim_{x→∞}\ln y=0.\) como a função logarítmica natural é contínua, concluímos que

\[\ln\left(\lim_{x→∞}y\right)=0, \nonumber \]

o que leva a

\[\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\lim_{x→∞}y\right)}=e^0=1. \nonumber \]

Portanto,

\[\lim_{x→∞}x^{1/x}=1. \nonumber \]

Exercício\(\PageIndex{6}\)

Avalie\[\lim_{x→∞}x^{1/\ln(x)}. \nonumber \]

Dica

Deixe\(y=x^{1/\ln(x)}\) e aplique o logaritmo natural nos dois lados da equação.

Resposta

\(e\)

Exemplo\(\PageIndex{7}\): Indeterminate Form of Type \(0^0\)

Avalie\[\lim_{x→0^+}x^{\sin x}. \nonumber \]

Solução

Deixe

\[y=x^{\sin x}. \nonumber \]

Portanto,

\[\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber \]

Agora avaliamos\(\displaystyle\lim_{x→0^+}\sin x\ln x.\) Desde\(\displaystyle\lim_{x→0^+}\sin x=0\) e\(\displaystyle\lim_{x→0^+}\ln x=−∞\), temos a forma indeterminada\(0⋅∞\). Para aplicar a regra de L'Hôpital, precisamos reescrever\(\sin x\ln x\) como uma fração. Nós poderíamos escrever

\[\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber \]

ou

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber \]

Vamos considerar a primeira opção. Nesse caso, aplicando a regra de L'Hôpital, obteríamos

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber \]

Infelizmente, não temos apenas outra expressão envolvendo a forma indeterminada,\(0⋅∞,\) mas o novo limite é ainda mais complicado de avaliar do que aquele com o qual começamos. Em vez disso, tentamos a segunda opção. Ao escrever

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber \]

e aplicando a regra de L'Hôpital, obtemos

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber \]

Usando o fato de que\(\csc x=\dfrac{1}{\sin x}\) e\(\cot x=\dfrac{\cos x}{\sin x}\), podemos reescrever a expressão no lado direito como

\[\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber \]

Concluímos que\(\displaystyle\lim_{x→0^+}\ln y=0.\) Portanto,\(\displaystyle\ln\left(\lim_{x→0^+}y\right)=0\) e temos

\[\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber \]

Portanto,

\[\lim_{x→0^+}x^{\sin x}=1. \nonumber \]

Exercício\(\PageIndex{7}\)

Avalie\(\displaystyle \lim_{x→0^+}x^x\).

Dica

Deixe\(y=x^x\) e pegue o logaritmo natural de ambos os lados da equação.

Resposta

1

Taxas de crescimento de funções

Suponha que as funções\(f\) e\(g\) ambas se aproximem do infinito como\(x→∞\). Embora os valores de ambas as funções se tornem arbitrariamente grandes à medida que os valores de\(x\) se tornam suficientemente grandes, às vezes uma função está crescendo mais rapidamente do que a outra. Por exemplo,\(f(x)=x^2\) e\(g(x)=x^3\) ambos se aproximam do infinito como\(x→∞\). No entanto, como\(\PageIndex{1}\) mostra a Tabela, os valores de\(x^3\) estão crescendo muito mais rápido do que os valores de\(x^2\).

Tabela\(\PageIndex{1}\): Comparando as taxas de crescimento de\(x^2\) e\(x^3\)

\(x\)	10	100	1000	10.000
\(f(x)=x^2\)	100	10.000	1.000.000	100.000.000
\(g(x)=x^3\)	1000	1.000.000	1.000.000.000	1.000.000.000.000

Na verdade,

\[\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber \]

ou, equivalentemente

\[\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber \]

Como resultado, dizemos que\(x^3\) está crescendo mais rapidamente do que\(x^2\) como\(x→∞\). Por outro lado, para\(f(x)=x^2\) e\(g(x)=3x^2+4x+1\), embora os valores de\(g(x)\) sejam sempre maiores que os valores de\(f(x)\) for\(x>0\), cada valor de\(g(x)\) é aproximadamente três vezes o valor correspondente de\(f(x)\) as\(x→∞\), conforme mostrado na Tabela\(\PageIndex{2}\). Na verdade,

\[\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber \]

Tabela\(\PageIndex{2}\): Comparando as taxas de crescimento de\(x^2\) e\(3x^2+4x+1\)

\(x\)	10	100	1000	10.000
\(f(x)=x^2\)	100	10.000	1.000.000	100.000.000
\(g(x)=3x^2+4x+1\)	341	30.401	3.004.001	300.040.001

Nesse caso, dizemos isso\(x^2\) e\(3x^2+4x+1\) estamos crescendo na mesma proporção que\(x→∞.\)

De forma mais geral, suponha\(f\) e\(g\) sejam duas funções que se aproximam do infinito como\(x→∞\). Dizemos que\(g\) cresce mais rápido do que\(f\) como\(x→∞\) se

\[\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber \]

Por outro lado, se existe uma constante\(M≠0\) tal

\[\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber \]

dizemos\(f\) e\(g\) crescemos na mesma proporção que\(x→∞\).

A seguir, veremos como usar a regra de L'Hôpital para comparar as taxas de crescimento das funções de potência, exponenciais e logarítmicas.

Exemplo\(\PageIndex{8}\): Comparing the Growth Rates of \(\ln(x)\), \(x^2\), and \(e^x\)

Para cada um dos seguintes pares de funções, use a regra de L'Hôpital para avaliar\[\lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber \]

1. \(f(x)=x^2\)e\(g(x)=e^x\)
2. \(f(x)=\ln(x)\)e\(g(x)=x^2\)

Solução

a. Desde\(\displaystyle \lim_{x→∞}x^2=∞\) e\(\displaystyle \lim_{x→∞}e^x=∞\), podemos usar a regra de L'Hôpital para avaliar\(\displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]\). Nós obtemos

\[\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber \]

Desde\(\displaystyle \lim_{x→∞}2x=∞\) e\(\displaystyle \lim_{x→∞}e^x=∞\), podemos aplicar a regra de L'Hôpital novamente. Desde

\[\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber \]

concluímos que

\[\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber \]

Portanto,\(e^x\) cresce mais rapidamente do que\(x^2\) como\(x→∞\) (Veja a Figura\(\PageIndex{3}\) e a Tabela\(\PageIndex{3}\))

Figura\(\PageIndex{3}\): Uma função exponencial cresce a uma taxa mais rápida do que uma função de potência.

Tabela\(\PageIndex{3}\): Taxas de crescimento de uma função de potência e uma função exponencial.

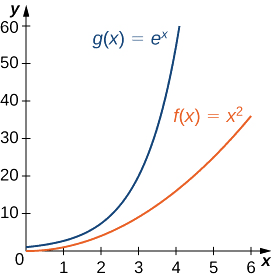
\(x\)	5	10	15	20
\(x^2\)	25	100	225	400
\(e^x\)	148	22.026	3.269.017	485.165.195

b. Desde\(\displaystyle \lim_{x→∞}\ln x=∞\) e\(\displaystyle \lim_{x→∞}x^2=∞\), podemos usar a regra de L'Hôpital para avaliar\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}\). Nós obtemos

\[\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber \]

Assim,\(x^2\) cresce mais rapidamente do que\(\ln x\) as\(x→∞\) (veja a Figura\(\PageIndex{4}\) e a Tabela\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): Uma função de potência cresce a uma taxa mais rápida do que uma função logarítmica.

Tabela\(\PageIndex{4}\): Taxas de crescimento de uma função de potência e uma função logarítmica

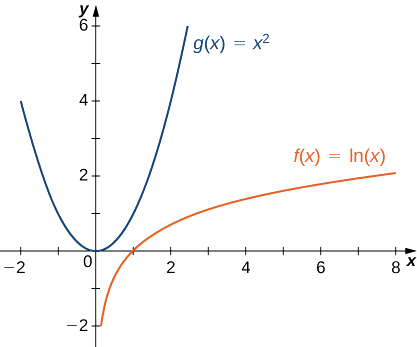
\(x\)	10	100	1000	10.000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(x^2\)	100	10.000	1.000.000	100.000.000

Exercício\(\PageIndex{8}\)

Compare as taxas de crescimento de\(x^{100}\)\(2^x\) e.

Dica

Aplique a regra do L'Hôpital para\(x^{100}/2^x\).

Resposta

A função\(2^x\) cresce mais rápido do que\(x^{100}\).

Usando as mesmas ideias do Exemplo\(\PageIndex{8}a\), não é difícil mostrar que\(e^x\) cresce mais rapidamente do que\(x^p\) qualquer outra\(p>0\). Na Figura\(\PageIndex{5}\) e na Tabela\(\PageIndex{5}\), comparamos\(e^x\) com\(x^3\) e\(x^4\) como\(x→∞\).

Figura\(\PageIndex{5}\): A função exponencial\(e^x\) cresce mais rápido do que\(x^p\) qualquer outra\(p>0\). (a) Uma comparação de\(e^x\) com\(x^3\). (b) Uma comparação de\(e^x\) com\(x^4\).

Tabela\(\PageIndex{5}\): Uma função exponencial cresce a uma taxa mais rápida do que qualquer função de potência

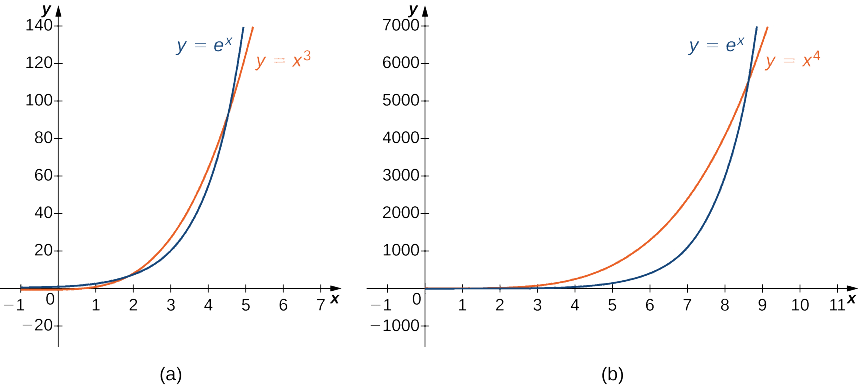
\(x\)	5	10	15	20
\(x^3\)	125	1000	3375	8000
\(x^4\)	625	10.000	50.625	160.000
\(e^x\)	148	22.026	3.269.017	485.165.195

Da mesma forma, não é difícil mostrar que\(x^p\) cresce mais rapidamente do que\(\ln x\) qualquer outra\(p>0\). Na Figura\(\PageIndex{6}\) e na Tabela\(\PageIndex{6}\), comparamos\(\ln x\) com\(\sqrt[3]{x}\)\(\sqrt{x}\) e.

Figura\(\PageIndex{6}\): A função\(y=\ln(x)\) cresce mais lentamente do que\(x^p\) qualquer outra\(p>0\)\(x→∞\).

Tabela\(\PageIndex{6}\): Uma função logarítmica cresce a uma taxa mais lenta do que qualquer função raiz

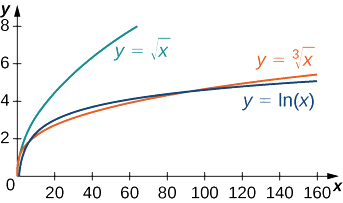
\(x\)	10	100	1000	10.000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(\sqrt[3]{x}\)	2.154	4.642	10	21.544
\(\sqrt{x}\)	3.162	10	31.623	100

Conceitos-chave

• A regra de L'Hôpital pode ser usada para avaliar o limite de um quociente quando a forma indeterminada\(\dfrac{0}{0}\) ou\(∞/∞\) surge.
• A regra de L'Hôpital também pode ser aplicada a outras formas indeterminadas se elas puderem ser reescritas em termos de um limite envolvendo um quociente que tenha a forma indeterminada\(\dfrac{0}{0}\) ou\(∞/∞.\)
• A função exponencial\(e^x\) cresce mais rápido do que qualquer função de potência\(x^p, p>0\).
• A função logarítmica\(\ln x\) cresce mais lentamente do que qualquer função de potência\(x^p, p>0\).

Glossário

formas indeterminadas

Ao avaliar um limite, os formulários,\(\dfrac{0}{0}\)\(∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0\), e\(1^∞\) são considerados indeterminados porque uma análise mais aprofundada é necessária para determinar se o limite existe e, em caso afirmativo, qual é seu valor.

Regra do L'Hôpital

Se\(f\) e\(g\) são funções diferenciáveis em um intervalo\(a\), exceto possivelmente em\(a\), e\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) ou\(\displaystyle \lim_{x→a}f(x)\) e\(\displaystyle \lim_{x→a}g(x)\) são infinitas, então\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}\), assumindo que o limite à direita existe ou é\(∞\) ou\(−∞\).