3.3: Regras de diferenciação
- Page ID
- 188494
- Defina a constante, o múltiplo constante e as regras de potência.
- Aplique as regras de soma e diferença para combinar derivadas.
- Use a regra do produto para encontrar a derivada de um produto de funções.
- Use a regra do quociente para encontrar a derivada de um quociente de funções.
- Estenda a regra de potência para funções com expoentes negativos.
- Combine as regras de diferenciação para encontrar a derivada de uma função polinomial ou racional.
Encontrar derivadas de funções usando a definição da derivada pode ser um processo longo e, para certas funções, bastante desafiador. Por exemplo, anteriormente descobrimos que
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
usando um processo que envolvia a multiplicação de uma expressão por um conjugado antes de avaliar um limite.
O processo que poderíamos usar para avaliar\(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) usando a definição, embora semelhante, é mais complicado.
Nesta seção, desenvolvemos regras para encontrar derivadas que nos permitem contornar esse processo. Começamos com o básico.
As regras básicas
As funções\(f(x)=c\) e\(g(x)=x^n\) onde\(n\) é um número inteiro positivo são os blocos de construção a partir dos quais todos os polinômios e funções racionais são construídos. Para encontrar derivadas de polinômios e funções racionais de forma eficiente sem recorrer à definição limite da derivada, devemos primeiro desenvolver fórmulas para diferenciar essas funções básicas.
A regra constante
Primeiro, aplicamos a definição de limite da derivada para encontrar a derivada da função constante,\(f(x)=c\). Para essa função, tanto\(f(x)=c\) quanto\(f(x+h)=c\), então obtemos o seguinte resultado:
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
A regra para diferenciar funções constantes é chamada de regra constante. Ele afirma que a derivada de uma função constante é zero; ou seja, como uma função constante é uma linha horizontal, a inclinação, ou a taxa de variação, de uma função constante é\(0\). Reafirmamos essa regra no seguinte teorema.
\(c\)Seja uma constante. Se\(f(x)=c\), então\(f′(x)=0.\)
Como alternativa, podemos expressar essa regra como
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Encontre a derivada de\(f(x)=8.\)
Solução
Esta é apenas uma aplicação da regra em uma etapa:\(f′(8)=0.\)
Encontre a derivada de\(g(x)=−3\).
- Dica
-
Use o exemplo anterior como guia
- Responda
-
0
A regra do poder
Nós mostramos que
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
Nesse ponto, você pode ver um padrão começando a se desenvolver para derivadas do formulário\(\dfrac{d}{dx}\left(x^n\right)\). Continuamos nosso exame de fórmulas derivadas diferenciando funções de potência da forma\(f(x)=x^n\) onde\(n\) está um número inteiro positivo. Desenvolvemos fórmulas para derivadas desse tipo de função em etapas, começando com potências inteiras positivas. Antes de declarar e provar a regra geral para derivadas de funções dessa forma, examinamos um caso específico,\(\dfrac{d}{dx}(x^3)\). À medida que examinamos essa derivação, preste atenção especial à parte da expressão em negrito, pois a técnica usada neste caso é essencialmente a mesma usada para provar o caso geral.
Encontre\(\dfrac{d}{dx}\left(x^3\right)\).
Solução:
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Observe que o primeiro termo na expansão de\((x+h)^3\) é\(x^3\) e o segundo termo é\(3x^2h\). Todos os outros termos contêm poderes de\(h\) dois ou mais. |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | Nesta etapa, os\(x^3\) termos foram cancelados, restando apenas os termos contendo\(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Considere o fator comum de\(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | Depois de cancelar o fator comum de\(h\), o único termo que não contém\(h\) é\(3x^2\). |
| \(=3x^2\) | Deixe\(h\) ir para\(0\). |
Encontre\(\dfrac{d}{dx}\left(x^4\right).\)
- Dica
-
Use\((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) e siga o procedimento descrito no exemplo anterior.
- Responda
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
Como veremos, o procedimento para encontrar a derivada da forma geral\(f(x)=x^n\) é muito semelhante. Embora muitas vezes não seja sensato tirar conclusões gerais de exemplos específicos, notamos que quando diferenciamos\(f(x)=x^3\), a potência ligada\(x\) se torna o coeficiente de\(x^2\) na derivada e a potência\(x\) na derivada diminui em 1. O teorema a seguir afirma que a regra da potência vale para todas as potências inteiras positivas de\(x\). Eventualmente, estenderemos esse resultado para potências inteiras negativas. Posteriormente, veremos que essa regra também pode ser estendida primeiro aos poderes racionais de\(x\) e depois aos poderes arbitrários de\(x\). Esteja ciente, no entanto, de que essa regra não se aplica a funções nas quais uma constante é elevada a uma potência variável, como\(f(x)=3^x\).
\(n\)Seja um número inteiro positivo. Se\(f(x)=x^n\), então
\[f′(x)=nx^{n−1}. \nonumber \]
Como alternativa, podemos expressar essa regra como
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
Para\(f(x)=x^n\) onde\(n\) está um número inteiro positivo, temos
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Desde
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
nós vemos isso
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
Em seguida, divida os dois lados por h:
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Assim,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Finalmente,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Encontre a derivada da função\(f(x)=x^{10}\) aplicando a regra da potência.
Solução
Usando a regra de potência com\(n=10\), obtemos
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Encontre a derivada de\(f(x)=x^7\).
- Dica
-
Use a regra de potência com\(n=7.\)
- Responda
-
\(f′(x)=7x^6\)
A soma, a diferença e as regras múltiplas constantes
Encontramos nossas próximas regras de diferenciação observando derivadas de somas, diferenças e múltiplos constantes de funções. Assim como quando trabalhamos com funções, existem regras que facilitam encontrar derivadas de funções que adicionamos, subtraímos ou multiplicamos por uma constante. Essas regras estão resumidas no seguinte teorema.
Seja\(f(x)\) e\(g(x)\) seja funções diferenciáveis e\(k\) seja uma constante. Então, cada uma das seguintes equações é válida.
Regra de soma. A derivada da soma de uma função\(f\) e uma função\(g\) é igual à soma da derivada de\(f\) e da derivada de\(g\).
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
ou seja,
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Regra da diferença. A derivada da diferença entre uma função\(f\) e uma função\(g\) é a mesma que a diferença entre a derivada de\(f\) e a derivada de\(g\):
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
ou seja,
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Regra múltipla constante. A derivada de uma constante\(k\) multiplicada por uma função\(f\) é a mesma que a constante multiplicada pela derivada:
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
ou seja,
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
Fornecemos apenas a prova da regra da soma aqui. O resto segue de maneira semelhante.
Para funções diferenciáveis\(f(x)\) e\(g(x)\), nós definimos\(s(x)=f(x)+g(x)\). Usando a definição de limite da derivada, temos
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
Ao substituir\(s(x+h)=f(x+h)+g(x+h)\) e\(s(x)=f(x)+g(x),\) obtemos
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
Reorganizando e reagrupando os termos, temos
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
Agora aplicamos a lei da soma para limites e a definição da derivada a ser obtida
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
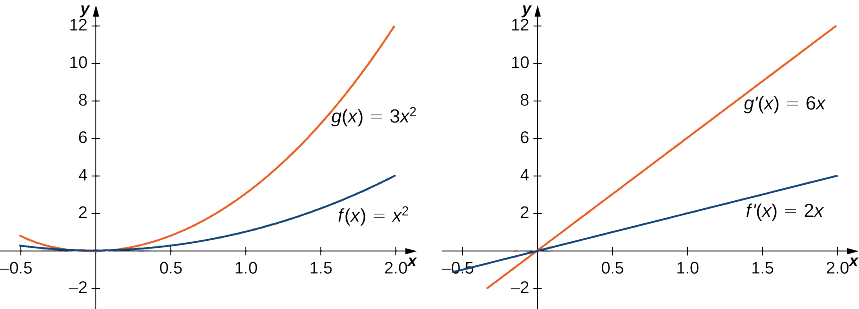
Encontre a derivada de\(g(x)=3x^2\) e compare-a com a derivada de\(f(x)=x^2.\)
Solução
Usamos a regra de potência diretamente:
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Como\(f(x)=x^2\) tem derivada\(f′(x)=2x\), vemos que a derivada de\(g(x)\) é 3 vezes a derivada de\(f(x)\). Essa relação é ilustrada na Figura\(\PageIndex{1}\).
Encontre a derivada de\(f(x)=2x^5+7\).
Solução
Começamos aplicando a regra para diferenciar a soma de duas funções, seguida pelas regras para diferenciar múltiplos constantes de funções e a regra para diferenciar potências. Para entender melhor a sequência na qual as regras de diferenciação são aplicadas, usamos a notação de Leibniz em toda a solução:
\ (\ begin {align*} f′( x) &=\ dfrac {d} {dx}\ left (2x^5+7\ right)\\ [4pt]
&=\ dfrac {d} {dx} (2x^5) +\ dfrac {d} {dx} (7) & &\ text {Aplique a regra da soma.}\\ [4pt]
&=2\ dfrac {d} {dx} (x^5) +\ dfrac {d} {dx} (7) & &\ text {Aplique a regra múltipla constante.}\\ [4pt]
&=2 (5 x^4) +0 & &\ text {Aplique a regra de potência e a regra constante.}\\ [4pt]
&=10x^4 & &\ text {Simplifique.} \ end {align*}\)
Encontre a derivada de\(f(x)=2x^3−6x^2+3.\)
- Dica
-
Use o exemplo anterior como guia.
- Resposta
-
\(f′(x)=6x^2−12x.\)
Encontre a equação da reta tangente ao gráfico de\(f(x)=x^2−4x+6\) em\(x=1\)
Solução
Para encontrar a equação da reta tangente, precisamos de um ponto e uma inclinação. Para encontrar o ponto, calcule
\[f(1)=1^2−4(1)+6=3. \nonumber \]
Isso nos dá o ponto\((1,3)\). Como a inclinação da reta tangente em 1 é\(f′(1)\), devemos primeiro encontrar\(f′(x)\). Usando a definição de uma derivada, temos
\[f′(x)=2x−4\nonumber \]
então a inclinação da reta tangente é\(f′(1)=−2\). Usando a fórmula de inclinação do ponto, vemos que a equação da reta tangente é
\[y−3=−2(x−1).\nonumber \]
Colocando a equação da reta na forma de interceptação de inclinação, obtemos
\[y=−2x+5.\nonumber \]
Encontre a equação da reta tangente ao gráfico de\(f(x)=3x^2−11\) at\(x=2\). Use a forma de inclinação de pontos.
- Dica
-
Use o exemplo anterior como guia.
- Resposta
-
\(y=12x−23\)
A regra do produto
Agora que examinamos as regras básicas, podemos começar a examinar algumas das regras mais avançadas. O primeiro examina a derivada do produto de duas funções. Embora possa ser tentador supor que a derivada do produto seja o produto das derivadas, semelhante às regras de soma e diferença, a regra do produto não segue esse padrão. Para ver por que não podemos usar esse padrão, considere a função\(f(x)=x^2\), cuja derivada é\(f′(x)=2x\) e não\(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
Seja\(f(x)\) e\(g(x)\) seja funções diferenciáveis. Então
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
Ou seja,
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
Isso significa que a derivada de um produto de duas funções é a derivada da primeira função vezes a segunda função mais a derivada da segunda função vezes a primeira função.
Começamos assumindo que\(f(x)\) e\(g(x)\) são funções diferenciáveis. Em um ponto chave dessa prova, precisamos usar o fato de que\(g(x)\), por ser diferenciável, também é contínuo. Em particular, usamos o fato de que, uma vez que\(g(x)\) é contínuo,\(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
Ao aplicar a definição de limite da derivada,\(p(x)=f(x)g(x),\) obtemos
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Ao somar e subtrair\(f(x)g(x+h)\) o numerador, temos
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Depois de separar esse quociente e aplicar a lei da soma para limites, a derivada se torna
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Reorganizando, obtemos
\ [\ begin {align*} p′( x) &=\ lim_ {h→0}\ esquerda (\ dfrac {f (x+h) −f (x)} {h} ⋅g (x+h)\ direita) +\ lim_ {h→0}\ esquerda (\ dfrac {g (x+h) −g (x)} {h} ⋅f (x)\ direita)\\ [4pt]
&=\ left (\ lim_ {h→0}\ dfrac {f (x+h) −f (x)} {h}\ direita) ‣\ esquerda (\ lim_ {h→0}\; g (x+h)\ direita) +\ esquerda (\ lim_ {h→0}\ dfrac {g (x+h) −g (x)} {h}\ direita) ⋅f (x)\ end {align*}\]
Usando a continuidade de\(g(x)\), a definição das derivadas de\(f(x)\) e e e\(g(x)\) aplicando as leis de limite, chegamos à regra do produto,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
Para\(p(x)=f(x)g(x)\), use a regra do produto para descobrir\(p′(2)\) se\(f(2)=3,\; f′(2)=−4,\; g(2)=1\),\(g′(2)=6\) e.
Solução
Desde\(p′(x)=f′(x)g(x)+g′(x)f(x),\) e\(p(x)=f(x)g(x)\), portanto,
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
Para\(p(x)=(x^2+2)(3x^3−5x),\) encontrar\(p′(x)\) aplicando a regra do produto. Verifique o resultado encontrando primeiro o produto e depois diferenciando.
Solução
Se definirmos\(f(x)=x^2+2\) e\(g(x)=3x^3−5x\), então\(f′(x)=2x\)\(g′(x)=9x^2−5\) e. Assim,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
Simplificando, temos
\[p′(x)=15x^4+3x^2−10. \nonumber \]
Para verificar, vemos isso\(p(x)=3x^5+x^3−10x\) e, consequentemente,\(p′(x)=15x^4+3x^2−10.\)
Use a regra do produto para obter a derivada de\(p(x)=2x^5(4x^2+x).\)
- Dica
-
Defina\(f(x)=2x^5\)\(g(x)=4x^2+x\) e use o exemplo anterior como guia.
- Resposta
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
A regra do quociente
Tendo desenvolvido e praticado a regra do produto, agora consideramos diferenciar quocientes de funções. Como vemos no teorema a seguir, a derivada do quociente não é o quociente das derivadas; ao contrário, é a derivada da função no numerador vezes a função no denominador menos a derivada da função no denominador vezes a função no numerador, tudo dividido por o quadrado da função no denominador. Para entender melhor por que não podemos simplesmente tomar o quociente das derivadas, tenha em mente que
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
Seja\(f(x)\) e\(g(x)\) seja funções diferenciáveis. Então
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
Ou seja, se
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
depois
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
A prova da regra do quociente é muito semelhante à prova da regra do produto, então ela é omitida aqui. Em vez disso, aplicamos essa nova regra para encontrar derivadas no próximo exemplo.
Use a regra do quociente para encontrar a derivada de\(q(x)=\dfrac{5x^2}{4x+3}.\)
Solução
Deixe\(f(x)=5x^2\)\(g(x)=4x+3\) e. Assim,\(f′(x)=10x\)\(g′(x)=4\) e.
Substituindo na regra do quociente, temos
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
Simplificando, obtemos
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Encontre a derivada de\(h(x)=\dfrac{3x+1}{4x−3}\).
- Dica
-
Aplique a regra do quociente com\(f(x)=3x+1\)\(g(x)=4x−3\) e.
- Resposta
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
Agora é possível usar a regra do quociente para estender a regra da potência e encontrar derivadas de funções da forma\(x^k\) onde\(k\) está um número inteiro negativo.
Se\(k\) for um número inteiro negativo, então
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
Se\(k\) for um número inteiro negativo, podemos definir\(n=−k\), de forma que n seja um inteiro positivo com\(k=−n\). Já que para cada número inteiro positivo\(n\)\(x^{−n}=\dfrac{1}{x^n}\),, agora podemos aplicar a regra do quociente definindo\(f(x)=1\)\(g(x)=x^n\) e. Nesse caso,\(f′(x)=0\)\(g′(x)=nx^{n−1}\) e. Assim,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
Simplificando, vemos que
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Finalmente, observe que\(k=−n\), uma vez que, ao substituir, temos
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Encontre\(\dfrac{d}{dx}(x^{−4})\).
Solução
Ao aplicar a regra de potência estendida com\(k=−4\), obtemos
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Use a regra de potência estendida e a regra múltipla constante para encontrar\(f(x)=\dfrac{6}{x^2}\).
Solução
Pode parecer tentador usar a regra do quociente para encontrar essa derivada, e certamente não seria incorreto fazer isso. No entanto, é muito mais fácil diferenciar essa função reescrevendo-a primeiro como\(f(x)=6x^{−2}\).
\ (\ begin {align*} f′( x) &=\ dfrac {d} {dx}\ left (\ dfrac {6} {x^2}\ right) =\ dfrac {d} {dx}\ left (6x^ {−2}\ right) & &\ text {Reescrever}\ dfrac {6} {x^2}\ texto {como 6} x^ {−2}.\\ [4pt]
&=6\ dfrac {d} {dx}\ left (x^ {−2}\ right) & &\ text {Aplique a regra múltipla constante.}\\ [4pt]
&=6 (−2x^ { −3}) & &\ text {Use a regra de potência estendida para diferenciar} x^ {−2}.\\ [4pt]
&=−12x^ {−3} & &\ text {Simplifique.} \ end {align*}\)
Encontre a derivada de\(g(x)=\dfrac{1}{x^7}\) usar a regra de potência estendida.
- Dica
-
Reescrever\(g(x)=\dfrac{1}{x^7}=x^{−7}\). Use a regra de potência estendida com\(k=−7\).
- Resposta
-
\(g′(x)=−7x^{−8}\).
Combinando regras de diferenciação
Como vimos nos exemplos desta seção, raramente acontece que sejamos chamados a aplicar apenas uma regra de diferenciação para encontrar a derivada de uma determinada função. Nesse ponto, combinando as regras de diferenciação, podemos encontrar as derivadas de qualquer função polinomial ou racional. Posteriormente, encontraremos combinações mais complexas de regras de diferenciação. Uma boa regra prática a ser usada ao aplicar várias regras é aplicar as regras no sentido inverso da ordem em que avaliaríamos a função.
Para\(k(x)=3h(x)+x^2g(x)\), encontre\(k′(x)\).
Solução: encontrar essa derivada requer a regra da soma, a regra do múltiplo constante e a regra do produto.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Aplique a regra da soma. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Aplique a regra do múltiplo constante para diferenciar\(3h(x)\) e a regra do produto para diferenciar\(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
\(k(x)=f(x)g(x)h(x)\)Pois, expresse\(k′(x)\) em termos de\(f(x),g(x),h(x)\) e seus derivados.
Solução
Podemos pensar na função\(k(x)\) como o produto da função\(f(x)g(x)\) e da função\(h(x)\). Isso é,\(k(x)=(f(x)g(x))⋅h(x)\). Assim,
\ (\ begin {align*} k′( x) &=\ dfrac {d} {dx}\ big (f (x) g (x)\ big) ⋅h (x) +\ dfrac {d} {dx}\ big (h (x)\ big) ▸\ big (f (x) g (x)\ big). & &\ text {Aplique a regra do produto ao produto de} f (x) g (x)\ text {e} h (x).\\ [4pt]
&=\ big (f′( x) g (x) +g′( x) f (x)\ big) h (x) +h′( x) f (x) g (x) &\ text {Aplicar a regra do produto a} f (x) g (x)\\ [4pt]
&=f′( x) g (x) h (x) +f (x) g′( x) h (x) +f (x) g (x) h′( x). & &\ text {Simplifique.} \ end {align*}\)
Para\(h(x)=\dfrac{2x^3k(x)}{3x+2}\), encontre\(h′(x)\).
Solução
Esse procedimento é típico para encontrar a derivada de uma função racional.
\ (\ begin {align*} h′( x) &=\ dfrac {\ dfrac {d} {dx} (2x^3k (x)) □ (3x+2) −\ dfrac {d} {dx} (3x+2) ≠ (2x^3k (x))} {(3x+2) ^2} & &\ text {Aplicar o regra do quociente.}\\ [4pt]
&=\ dfrac {(6x^2k (x) +k′( x) ⋅2x^3) (3x+2) −3 (2x^3k (x))} {(3x+2) ^2} & &\ text {Aplique a regra do produto para encontrar}\ dfrac {d} {dx} (2xx} (2xx} ^3 (x). \ text {Usar}\ dfrac {d} {dx} (3x+2) =3.\\ [4pt]
&=\ dfrac {−6x^3k (x) +18x^3k (x) +12x^2k (x) +6x^4k′( x) +4x^3k′( x)} {(3x+2) ^2} & &\ text {Simplifique}\ end {align*}\)
Encontre\(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Dica
-
Aplique a regra da diferença e a regra múltipla constante.
- Resposta
-
\(3f′(x)−2g′(x).\)
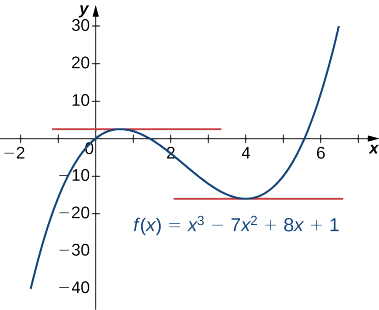
Determine os valores de\(x\) para os quais\(f(x)=x^3−7x^2+8x+1\) tem uma linha tangente horizontal.
Solução
Para encontrar os valores dos\(x\) quais\(f(x)\) tem uma reta tangente horizontal, devemos resolver\(f′(x)=0\).
Uma vez que\(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
devemos resolver\((3x−2)(x−4)=0\). Assim, vemos que a função tem linhas tangentes horizontais em\(x=\dfrac{2}{3}\) e\(x=4\) conforme mostrado no gráfico a seguir.
A posição de um objeto em um eixo coordenado no momento\(t\) é dada por\(s(t)=\dfrac{t}{t^2+1}.\) Qual é a velocidade inicial do objeto?
Solução
Como a velocidade inicial é\(v(0)=s′(0),\) começar encontrando\(s′(t)\) aplicando a regra do quociente:
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
Depois de avaliar, vemos que\(v(0)=1.\)
Encontre os valores dos\(x\) quais a reta tangente ao gráfico de\(f(x)=4x^2−3x+2\) tem uma reta tangente paralela à linha\(y=2x+3.\)
- Dica
-
Resolver\(f′(x)=2\).
- Resposta
-
\(\dfrac{5}{8}\)
As corridas de carros de Fórmula 1 podem ser muito emocionantes de assistir e atrair muitos espectadores. Os designers de pistas de Fórmula 1 precisam garantir que haja espaço suficiente na arquibancada ao redor da pista para acomodar esses espectadores. No entanto, as corridas de carros podem ser perigosas e as considerações de segurança são fundamentais. As arquibancadas devem ser colocadas onde os espectadores não corram perigo caso o motorista perca o controle de um carro (Figura\(\PageIndex{3}\)).

A segurança é especialmente uma preocupação nas curvas. Se o motorista não diminuir a velocidade o suficiente antes de entrar na curva, o carro pode deslizar para fora da pista de corrida. Normalmente, isso resulta apenas em uma curva mais larga, o que diminui a velocidade do motorista. Mas se o motorista perder o controle completamente, o carro pode sair completamente da pista, em um caminho tangente à curva da pista.
Suponha que você esteja criando uma nova faixa de Fórmula 1. Uma seção da pista pode ser modelada pela função\(f(x)=x^3+3x^2+x\) (Figura\(\PageIndex{4}\)). O plano atual prevê a construção de arquibancadas ao longo da primeira reta e em torno de uma parte da primeira curva. Os planos exigem que o canto frontal da arquibancada seja localizado no ponto (\(−1.9,2.8\)). Queremos determinar se esse local coloca os espectadores em perigo se o motorista perder o controle do carro.
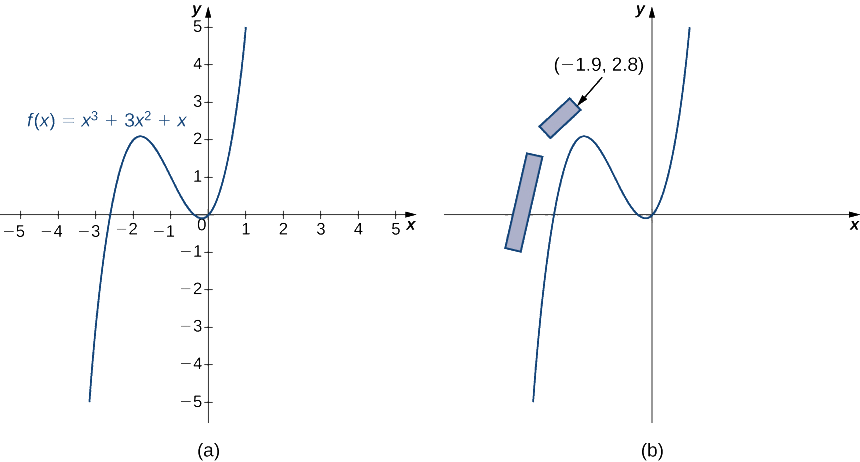
- Os físicos determinaram que os motoristas têm maior probabilidade de perder o controle de seus carros ao entrarem em uma curva, no ponto em que a inclinação da reta tangente é 1. Encontre as\((x,y)\) coordenadas desse ponto perto da curva.
- Encontre a equação da reta tangente à curva neste ponto.
- Para determinar se os espectadores estão em perigo nesse cenário, encontre a\(x\) coordenada -do ponto em que a reta tangente cruza a linha\(y=2.8\). Este ponto está seguro à direita da arquibancada? Ou os espectadores estão em perigo?
- E se um motorista perder o controle antes do projeto do físico? Suponha que um motorista perca o controle no ponto (\(−2.5,0.625\)). Qual é a inclinação da reta tangente nesse ponto?
- Se um motorista perder o controle conforme descrito na parte 4, os espectadores estão seguros?
- Você deve prosseguir com o design atual da arquibancada ou as arquibancadas devem ser movidas?
Conceitos-chave
- A derivada de uma função constante é zero.
- A derivada de uma função de potência é uma função na qual a potência ligada\(x\) se torna o coeficiente do termo e a potência\(x\) ligada na derivada diminui em 1.
- A derivada de uma constante\(c\) multiplicada por uma função\(f\) é a mesma que a constante multiplicada pela derivada.
- A derivada da soma de uma função\(f\) e uma função\(g\) é igual à soma da derivada de\(f\) e da derivada de\(g\).
- A derivada da diferença entre uma função\(f\) e uma função\(g\) é a mesma que a diferença entre a derivada de\(f\) e a derivada de\(g\).
- A derivada de um produto de duas funções é a derivada da primeira função vezes a segunda função mais a derivada da segunda função vezes a primeira função.
- A derivada do quociente de duas funções é a derivada da primeira função vezes a segunda função menos a derivada da segunda função vezes a primeira função, todas divididas pelo quadrado da segunda função.
- Usamos a definição de limite da derivada para desenvolver fórmulas que nos permitem encontrar derivadas sem recorrer à definição da derivada. Essas fórmulas podem ser usadas individualmente ou em combinação umas com as outras.
Glossário
- regra múltipla constante
- a derivada de uma constante\(c\) multiplicada por uma função\(f\) é a mesma que a constante multiplicada pela derivada:\(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- regra constante
- a derivada de uma função constante é zero:\(\dfrac{d}{dx}(c)=0\), onde\(c\) é uma constante
- regra de diferença
- a derivada da diferença de uma função\(f\) e uma função\(g\) é a mesma que a diferença da derivada de\(f\) e da derivada de\(g\):\(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- regra de potência
- a derivada de uma função de potência é uma função na qual a potência\(x\) ligada se torna o coeficiente do termo e a potência\(x\) na derivada diminui em 1: Se\(n\) for um número inteiro, então\(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- regra do produto
- a derivada de um produto de duas funções é a derivada da primeira função vezes a segunda função mais a derivada da segunda função vezes a primeira função:\(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- regra do quociente
- a derivada do quociente de duas funções é a derivada da primeira função vezes a segunda função menos a derivada da segunda função vezes a primeira função, todas divididas pelo quadrado da segunda função:\(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- regra de soma
- a derivada da soma de uma função\(f\) e uma função\(g\) é a mesma que a soma da derivada de\(f\) e a derivada de\(g\):\(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)


