2.5: A definição precisa de um limite
- Page ID
- 188709
- Descreva a definição de épsilon-delta de um limite.
- Aplique a definição de épsilon-delta para encontrar o limite de uma função.
- Descreva as definições de épsilon-delta de limites unilaterais e limites infinitos.
- Use a definição de épsilon-delta para provar as leis de limite.
Até agora, você já progrediu da definição muito informal de limite na introdução deste capítulo para a compreensão intuitiva de um limite. Nesse ponto, você deve ter uma noção intuitiva muito forte do que significa o limite de uma função e como encontrá-lo. Nesta seção, convertemos essa ideia intuitiva de limite em uma definição formal usando uma linguagem matemática precisa. A definição formal de limite é possivelmente uma das definições mais desafiadoras que você encontrará no início de seu estudo de cálculo; no entanto, vale a pena fazer qualquer esforço para conciliá-la com sua noção intuitiva de limite. Entender essa definição é a chave que abre as portas para uma melhor compreensão do cálculo.
Quantificando a proximidade
Antes de declarar a definição formal de um limite, devemos introduzir algumas ideias preliminares. Lembre-se de que a distância entre dois pontos\(a\) e\(b\) em uma reta numérica é dada por |\(a−b\) |.
- A afirmação |\(f(x)−L |<ε\) pode ser interpretada como: A distância entre\(f(x)\) e\(L\) é menor que\(ε\).
- A afirmação\(0<|x−a|<δ\) pode ser interpretada como:\(x≠a\) e a distância entre\(x\) e\(a\) é menor que\(δ\).
Também é importante observar as seguintes equivalências para o valor absoluto:
- A declaração |\(f(x)−L|<ε\) é equivalente à declaração\(L−ε<f(x)<L+ε\).
- A declaração\(0<|x−a|<δ\) é equivalente à declaração\(a−δ<x<a+δ\)\(x≠a\) e.
Com esses esclarecimentos, podemos declarar a definição formal do limite épsilon-delta.
\(f(x)\)Seja definido para tudo\(x≠a\) em um intervalo aberto contendo\(a\). \(L\)Seja um número real. Então
\[\lim_{x→a}f(x)=L \nonumber \]
se, para cada um\(ε>0\), existe um\(δ>0\), tal que se\(0<|x−a|<δ\), então\(|f(x)−L|<ε\).
Essa definição pode parecer bastante complexa do ponto de vista matemático, mas fica mais fácil de entender se a dividirmos frase por frase. A afirmação em si envolve algo chamado quantificador universal (para cada\(ε>0\)), um quantificador existencial (existe um\(δ>0\)) e, por último, uma afirmação condicional (se\(0<|x−a|<δ\), então\(|f(x)−L|<ε)\). Vamos dar uma olhada na Tabela\(\PageIndex{1}\), que detalha a definição e traduz cada parte.
| Definição | Tradução |
|---|---|
| 1. Para cada\(ε>0\), | 1. Para cada distância positiva\(ε\) de\(L\), |
| 2. existe um\(δ>0\), | 2. Há uma distância positiva\(δ\) de\(a\), |
| 3. tal que | 3. tal que |
| 4. se\(0<|x−a|<δ\), então\(|f(x)−L|<ε\). | 4. se\(x\) está mais\(δ\) perto do que\(a\) e\(x≠a\), então\(f(x)\) está mais\(ε\) perto do que\(L\). |
Podemos entender melhor essa definição observando a definição geometricamente. \(\PageIndex{1}\)A figura mostra os valores possíveis de\(δ\) para várias opções de\(ε>0\) para uma determinada função\(f(x)\), um número\(a\) e um limite\(L\) em\(a\). Observe que, à medida que escolhemos valores menores de\(ε\) (a distância entre a função e o limite), sempre podemos encontrar um valor\(δ\) pequeno o suficiente para que, se tivermos escolhido um\(x\) valor dentro\(δ\) de de\(a\), o valor de\(f(x)\) esteja dentro\(ε\) do limite \(L\).
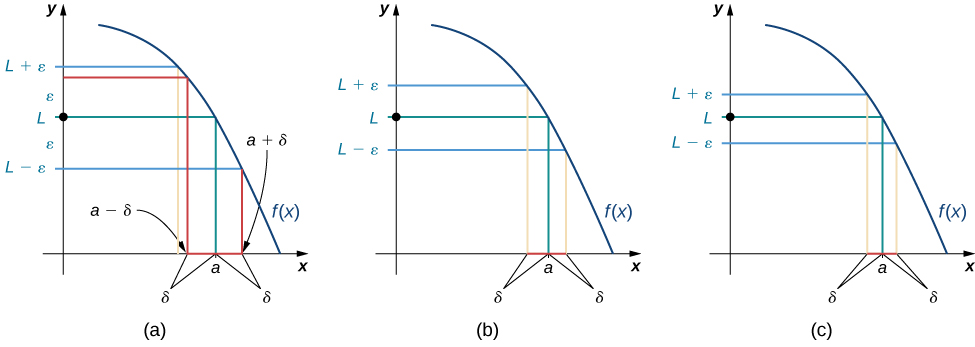
Visite o seguinte applet para experimentar encontrar valores de\(δ\) para valores selecionados de\(ε\):
\(\PageIndex{1}\)O exemplo mostra como você pode usar essa definição para provar uma afirmação sobre o limite de uma função específica em um valor especificado.
Prove isso\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
Solução
Deixe\(ε>0\).
A primeira parte da definição começa com “Para todos”\(ε>0\). Isso significa que devemos provar que tudo o que se segue é verdadeiro, não importa qual valor positivo\(ε\) seja escolhido. Ao declarar “Vamos”\(ε>0\), sinalizamos nossa intenção de fazer isso.
Escolha\(δ=\frac{ε}{2}\).
A definição continua com “existe um”\(δ>0\). A frase “existe” em uma declaração matemática é sempre um sinal para uma caça ao tesouro. Em outras palavras, devemos ir e encontrar\(δ\). Então, de onde exatamente\(δ=ε/2\) veio? Existem duas abordagens básicas para rastrear\(δ\). Um método é puramente algébrico e o outro é geométrico.
Começamos abordando o problema do ponto de vista algébrico. Como, em última análise\(|(2x+1)−3|<ε\), queremos, começamos manipulando essa expressão:\(|(2x+1)−3|<ε\) é equivalente a\(|2x−2|<ε\), que por sua vez é equivalente\(|2||x−1|<ε\) a. Por último, isso é equivalente\(|x−1|<ε/2\) a. Portanto, parece que\(δ=ε/2\) é apropriado.
Também podemos descobrir\(δ\) por meio de métodos geométricos. A figura\(\PageIndex{2}\) demonstra como isso é feito.
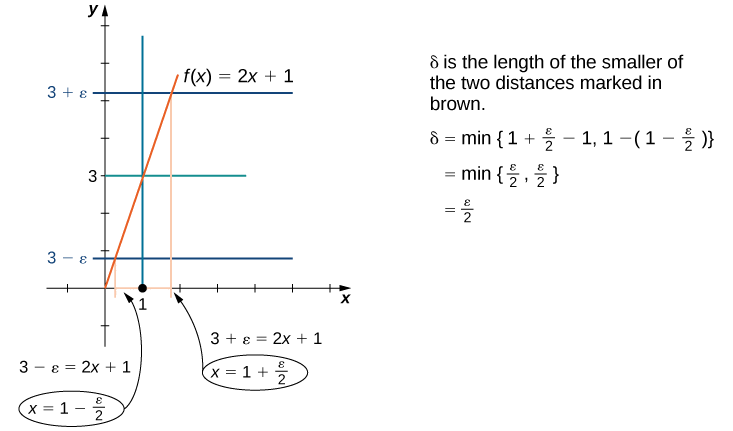
Suponha\(0<|x−1|<δ\). Quando\(δ\) foi escolhido, nosso objetivo é mostrar que se\(0<|x−1|<δ\), então\(|(2x+1)−3|<ε\). Para provar qualquer afirmação na forma “Se isso, então aquilo”, começamos assumindo “isso” e tentando obter “aquilo”.
Assim,
\(|(2x+1)−3|=|2x−2|\)propriedade de valor absoluto
\(=|2(x−1)|\)
\(=|2||x−1|\)\(|2|=2\)
\(=2|x−1|\)
\(<2⋅δ \)aqui é onde usamos a suposição de que\(0<|x−1|<δ\)
\(=2⋅\frac{ε}{2}=ε\)aqui é onde usamos nossa escolha de\(δ=ε/2\)
Análise
Nesta parte da prova, começamos\(|(2x+1)−3|\) e usamos nossa suposição\(0<|x−1|<δ\) em uma parte fundamental da cadeia de desigualdades\(|(2x+1)−3|\) para chegar a ser menor que ε. Poderíamos facilmente ter manipulado a suposta desigualdade\(0<|x−1|<δ\) para chegar ao\(|(2x+1)−3|<ε\) seguinte:
\(0<|x−1|<δ⇒|x−1|<δ\)
\(⇒−δ<x−1<δ\)
\(⇒−\frac{ε}{2}<x−1<\frac{ε}{2}\)
\(⇒−ε<2x−2<ε\)
\(⇒|2x−2|<ε\)
\(⇒|(2x+1)−3|<ε.\)
Portanto,\(\displaystyle \lim_{x→1} \;(2x+1)=3.\) (Depois de concluir a prova, declaramos o que realizamos.)
Depois de remover todas as observações, aqui está uma versão final da prova:
Deixe\(ε>0\).
Escolha\(δ=ε/2\).
Suponha\(0<|x−1|<δ\).
Assim,
\ (\ begin {align*} | (2x+1) −3| &= |2x−2|\ [4pt]
&=|2 (x−1) |\\ [4pt]
&=|2|x−1|\ [4pt]
&=2|x−1|\\ [4pt]
&<2⋅δ\\ [4pt]
&=2\ frac {ε} {2}\\ [4pt]
&=ε. \ end {align*}\)
Portanto,\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
A estratégia de solução de problemas a seguir resume o tipo de prova que elaboramos no Example\(\PageIndex{1}\).
- Vamos começar a prova com a seguinte declaração: Let\(ε>0\).
- Em seguida, precisamos obter um valor para\(δ\). Depois de obtermos esse valor, fazemos a seguinte declaração, preenchendo o espaço em branco com nossa opção de\(δ\): Escolha\(δ=\) _______.
- A próxima declaração na prova deve ser (neste momento, preenchemos nosso valor fornecido para\(a\)): Suponha\(0<|x−a|<δ\).
- Em seguida, com base nessa suposição, precisamos mostrar onde\(f(x)\) e\(L\) estão nossa função\(f(x)\) e nosso limite\(L\).\(|f(x)−L|<ε\) Em algum momento, precisamos usar\(0<|x−a|<δ\).
- Concluímos nossa prova com a declaração: Portanto,\(\displaystyle \lim_{x→a}f(x)=L\).
Complete a prova disso\(\displaystyle \lim_{x→−1}\;(4x+1)=−3\) preenchendo os espaços em branco.
Deixe _____.
Escolha\(δ=\) _______.
Suponha\(0<|x\) −_______|\(<δ\).
Assim, |________−________|=_________________________________\(ε\).
Solução
Começamos preenchendo os espaços em branco onde as opções são especificadas pela definição. Assim, temos
Deixe\(ε>0\).
Escolha\(δ\) =_______.
Suponha\(0<|x−(−1)|<δ\). (ou equivalentemente,\(0<|x+1|<δ\).)
Assim,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ\) _______\(ε\).
Focando na linha final da prova, vemos que devemos escolher\(δ=\frac{ε}{4}\).
Agora concluímos a redação final da prova:
Deixe\(ε>0\).
Escolha\(δ=\frac{ε}{4}\).
Suponha\(0<|x−(−1)|<δ\) (ou equivalentemente,\(0<|x+1|<δ\).)
Assim,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ=4(ε/4)=ε\).
Complete a prova disso\(\displaystyle \lim_{x→2}\;(3x−2)=4\) preenchendo os espaços em branco.
Deixe _______.
Escolha\(δ\) =_______.
Suponha\(0<|x−\) ____\(|<\) ____.
Assim,
|_______−____|\(=\) __________________________\(ε\).
Portanto,\(\displaystyle \lim_{x→2}\;(3x−2)=4\).
- Dica
-
Siga o esboço da Estratégia de Solução de Problemas que elaboramos na íntegra em Example\(\PageIndex{2}\).
- Responda
-
Deixar\(ε>0\); escolher\(δ=\frac{ε}{3}\); assumir\(0<|x−2|<δ\).
Assim,\(|(3x−2)−4|=|3x−6|=|3|⋅|x−2|<3⋅δ=3⋅(ε/3)=ε\).
Portanto,\(\displaystyle \lim_{x→2}(3x−2)=4\).
Em Exemplos\(\PageIndex{1}\) e\(\PageIndex{2}\), as provas foram bastante simples, pois as funções com as quais trabalhávamos eram lineares. No exemplo\(\PageIndex{3}\), vemos como modificar a prova para acomodar uma função não linear.
Prove isso\(\displaystyle \lim_{x→2}x^2=4\).
Solução
1. Deixe\(ε>0\). A primeira parte da definição começa com “Para cada”\(ε>0\), então devemos provar que tudo o que se segue é verdadeiro, não importa qual valor positivo\(ε\) seja escolhido. Ao declarar “Vamos”\(ε>0\), sinalizamos nossa intenção de fazer isso.
2. Sem perda de generalidade, suponha\(ε≤4\). Duas perguntas se apresentam: Por que queremos\(ε≤4\) e por que não há problema em fazer essa suposição? Em resposta à primeira pergunta: Mais tarde, no processo de solução para\(δ\), descobriremos que\(δ\) envolve a quantidade\(\sqrt{4−ε}\). Consequentemente, precisamos\(ε≤4\). Em resposta à segunda pergunta: Se conseguirmos descobrir\(δ>0\) que “funciona” para\(ε≤4\), então também “funcionará” para qualquer\(ε>4\) um. Lembre-se de que, embora seja sempre bom colocar um limite superior em ε, nunca é bom colocar um limite inferior (diferente de zero)\(ε\).
3. Escolha\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). A figura\(\PageIndex{3}\) mostra como fizemos essa escolha de\(δ\).
![Este gráfico mostra como encontrar geometricamente o delta de um determinado épsilon para a prova acima. Primeiro, a função f (x) = x^2 é extraída de [-1, 3]. No eixo y, o limite 4 proposto é marcado e a linha y=4 é desenhada para se cruzar com a função at (2,4). Para um determinado épsilon, o ponto 4 + épsilon e o 4 — épsilon estão marcados no eixo y acima e abaixo de 4. Linhas azuis são desenhadas a partir desses pontos para se cruzar com a função, onde linhas rosa são desenhadas do ponto de interseção com o eixo x. Essas linhas pousam em ambos os lados de x=2. Em seguida, resolvemos esses valores de x, que precisam ser positivos aqui. O primeiro é x^2 = 4 — épsilon, que simplifica para x = sqrt (4-épsilon). O próximo é x^2 = 4 + épsilon, o que simplifica para x = sqrt (4 + épsilon). Delta é a menor das duas distâncias, então é o mínimo de (2 — sqrt (4 — epsilon) e sqrt (4 + épsilon) — 2).](https://math.libretexts.org/@api/deki/files/12354/2.5.2.png)
4. Devemos mostrar: Se\(0<|x−2|<δ\)\(|x^2−4|<ε\), então, devemos começar assumindo
\(0<|x−2|<δ.\)
Nós realmente não precisamos\(0<|x−2|\) (em outras palavras\(x≠2\)) dessa prova. Desde então\(0<|x−2|<δ⇒|x−2|<δ\), não há problema em desistir\(0<|x−2|\).
\(|x−2|<δ.\)
Conseqüentemente,
\(−δ<x−2<δ.\)
Lembre-se disso\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). Assim,\(δ≥2−\sqrt{4−ε}\) e consequentemente\(−(2−\sqrt{4−ε})≤−δ\). Também usamos\(δ≤\sqrt{4+ε}−2\) aqui. Podemos perguntar neste momento: Por que\(2−\sqrt{4−ε}\) substituímos o\(δ\) lado esquerdo da desigualdade e o\(\sqrt{4+ε}−2\) lado direito da desigualdade? Se olharmos para a Figura\(\PageIndex{3}\), vemos que\(2−\sqrt{4−ε}\) corresponde à distância à\(2\) esquerda do\(x\) eixo -e\(\sqrt{4+ε}−2\) corresponde à distância à direita. Assim,
\(−(2−\sqrt{4−ε})≤−δ<x−2<δ≤\sqrt{4+ε}−2.\)
Simplificamos a expressão à esquerda:
\(−2+\sqrt{4−ε}<x−2<\sqrt{4+ε}−2\).
Em seguida, adicionamos 2 a todas as partes da desigualdade:
\(\sqrt{4−ε}<x<\sqrt{4+ε}.\)
Nós quadramos todas as partes da desigualdade. Não há problema em fazer isso, já que todas as partes da desigualdade são positivas:
\(4−ε<x^2<4+ε.\)
Subtraímos\(4\) de todas as partes da desigualdade:
\(−ε<x^2−4<ε.\)
Último,
\(|x^2−4|<ε.\)
5. Portanto,
\(\displaystyle \lim_{x→2}x^2=4.\)
Encontre δ correspondente a\(ε>0\) para uma prova de que\(\displaystyle \lim_{x→9}\sqrt{x}=3\).
- Dica
-
Desenhe um gráfico semelhante ao do Example\(\PageIndex{3}\).
- Responda
-
Escolha\(δ=\text{min}\{9−(3−ε)^2,\;(3+ε)^2−9\}\).
A abordagem geométrica para provar que o limite de uma função assume um valor específico funciona muito bem para algumas funções. Além disso, a visão da definição formal do limite que esse método fornece é inestimável. No entanto, também podemos abordar as provas de limite de um ponto de vista puramente algébrico. Em muitos casos, uma abordagem algébrica pode não apenas nos fornecer uma visão adicional da definição, mas também ser mais simples. Além disso, uma abordagem algébrica é a principal ferramenta usada em provas de declarações sobre limites. Por exemplo,\(\PageIndex{4}\), adotamos uma abordagem puramente algébrica.
Prove isso\(\displaystyle \lim_{x→−1}\;(x^2−2x+3)=6.\)
Solução
Vamos usar nosso esboço da Estratégia de Solução de Problemas:
1. Deixe\(ε>0\).
2. Escolha\(δ=\text{min}\{1,ε/5\}\). Essa escolha de\(δ\) pode parecer estranha à primeira vista, mas foi obtida examinando nossa desigualdade final desejada:\(∣(x^2−2x+3)−6∣<ε\). Essa desigualdade é equivalente\(|x+1|⋅|x−3|<ε\) a. Nesse ponto, a tentação de simplesmente escolher\(δ=\frac{ε}{x−3}\) é muito forte. Infelizmente, nossa escolha de\(δ\) deve depender somente de ε e de nenhuma outra variável. Se pudermos substituir\(|x−3|\) por um valor numérico, nosso problema poderá ser resolvido. Este é o lugar onde a suposição\(δ≤1\) entra em jogo. A escolha\(δ≤1\) daqui é arbitrária. Poderíamos ter usado com a mesma facilidade qualquer outro número positivo. Em algumas provas, pode ser necessário maior cuidado nessa escolha. Agora, desde então\(δ≤1\)\(|x+1|<δ≤1\), somos capazes de mostrar isso\(|x−3|<5\). Consequentemente,\(|x+1|⋅|x−3|<|x+1|⋅5\). Neste ponto, percebemos que também precisamos\(δ≤ε/5\). Assim, nós escolhemos\(δ=\text{min}\{1,ε/5\}\).
3. Suponha\(0<|x+1|<δ\). Assim,
\[|x+1|<1\text{ and }|x+1|<\frac{ε}{5}. \nonumber \]
Uma vez que\(|x+1|<1\), podemos concluir que\(−1<x+1<1\). Assim,\(4\) subtraindo de todas as partes da desigualdade, obtemos\(−5<x−3<−1\). Consequentemente,\(|x−3|<5\). Isso nos dá
\[\left|(x^2−2x+3)−6\right|=|x+1|⋅|x−3|<\frac{ε}{5}⋅5=ε.\nonumber \]
Portanto,
\[\lim_{x→−1}\;(x^2−2x+3)=6.\nonumber \]
Complete a prova de que\(\displaystyle \lim_{x→1}x^2=1\).
Deixar\(ε>0\); escolher\(δ=\text{min}\{1,ε/3\}\); assumir\(0<|x−1|<δ\).
Uma vez que\(|x−1|<1\), podemos concluir que\(−1<x−1<1\). Assim,\(1<x+1<3\). Conseqüentemente,\(|x+1|<3\).
- Dica
-
Use o exemplo\(\PageIndex{4}\) como guia.
- Responda
-
\(∣x^2−1∣=|x−1|⋅|x+1|<ε/3⋅3=ε\)
Você descobrirá que, em geral, quanto mais complexa uma função, maior a probabilidade de a abordagem algébrica ser a mais fácil de aplicar. A abordagem algébrica também é mais útil para provar afirmações sobre limites.
Provando leis de limite
Agora demonstramos como usar a definição épsilon-delta de um limite para construir uma prova rigorosa de uma das leis de limite. A desigualdade triangular é usada em um ponto chave da prova, então primeiro revisamos essa propriedade-chave de valor absoluto.
A desigualdade triangular afirma que se\(a\) e\(b\) são números reais, então\(|a+b|≤|a|+|b|\).
Provamos a seguinte lei de limite: Se\(\displaystyle \lim_{x→a}f(x)=L\) e\(\displaystyle \lim_{x→a}g(x)=M\), então\(\displaystyle \lim_{x→a}\;(f(x)+g(x))=L+M\).
Deixe\(ε>0\).
Escolha\(δ_1>0\) para que se\(0<|x−a|<δ_1\), então\(|f(x)−L|<ε/2\).
Escolha\(δ_2>0\) para que se\(0<|x−a|<δ_2\), então\(|g(x)−M|<ε/2\).
Escolha\(δ=\text{min}\{δ_1,δ_2\}\).
Suponha\(0<|x−a|<δ\).
Assim,
\(0<|x−a|<δ_1\)\(0<|x−a|<δ_2\)e.
Conseqüentemente,
\ [\ begin {alinhamento*} | (f (x) +g (x)) − (L+M) |&=| (f (x) −L) + (g (x) −M) |\ [4pt]
&≤|f (x) −L|+|G (x) −M|\\ [4pt]
&<\ frac {ε} {2} +\ frac {ε} {2} +\ frac {ε}} {2} =ε\ end {align*}. \ nonumber\]
□
Agora, exploramos o que significa não existir um limite. O limite\(\displaystyle \lim_{x→a}f(x)\) não existe se não houver um número real\(L\) para o qual\(\displaystyle \lim_{x→a}f(x)=L\). Portanto, para todos os números reais\(L\),\(\displaystyle \lim_{x→a}f(x)≠L\). Para entender o que isso significa, examinamos cada parte da definição de\(\displaystyle \lim_{x→a}f(x)=L\) junto com seu oposto. Uma tradução da definição é dada na Tabela\(\PageIndex{2}\).
| Definição | Oposto |
|---|---|
| 1. Para cada\(ε>0\), | 1. Existe\(ε>0\) para que |
| 2. existe um\(δ>0\), de modo que | 2. para cada\(δ>0\), |
| 3. se\(0<|x−a|<δ\), então\(|f(x)−L|<ε\). | 3. Existe uma\(x\) satisfação\(0<|x−a|<δ\) para que\(|f(x)−L|≥ε\). |
Finalmente, podemos afirmar o que significa não existir um limite. O limite\(\displaystyle \lim_{x→a}f(x)\) não existe se, para cada número real\(L\), existe um número real para\(ε>0\) que, para todos\(δ>0\), haja um\(x\) satisfatório\(0<|x−a|<δ\), de modo que\(|f(x)−L|≥ε\). Vamos aplicar isso no Exemplo\(\PageIndex{5}\) para mostrar que não existe um limite.
Mostre que\(\displaystyle \lim_{x→0}\frac{|x|}{x}\) isso não existe. O gráfico de\(f(x)=|x|/x\) é mostrado aqui:
0 e é uma linha sem inclinação que começa no eixo y em um círculo aberto (1,0)." src="https://math.libretexts.org/@api/dek...2355/2.5.3.png">
Solução
Suponha que\(L\) seja um candidato a um limite. Escolha\(ε=1/2\).
Deixe\(δ>0\). \(L≥0\)Ou\(L<0\). Se\(L≥0\), então deixe\(x=−δ/2\).
Assim,
\(|x−0|=∣−\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
e
\(\left|\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−L\right|=|−1−L|=L+1≥1>\frac{1}{2}=ε\).
Por outro lado, se\(L<0\), então deixe\(x=δ/2\). Assim,
\(|x−0|=∣\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
e
\(\left|\frac{∣\frac{δ}{2}∣}{\frac{δ}{2}}−L\right|=|1−L|=|L|+1≥1>\frac{1}{2}=ε\).
Assim, para qualquer valor de\(L\),\(\displaystyle \lim_{x→0}\frac{|x|}{x}≠L.\)
Limites unilaterais
Assim como primeiro obtivemos uma compreensão intuitiva dos limites e depois passamos para uma definição mais rigorosa de um limite, agora revisitamos os limites unilaterais. Para fazer isso, modificamos a definição de épsilon-delta de um limite para fornecer definições formais de epsilon-delta para limites da direita e da esquerda em um ponto. Essas definições exigem apenas pequenas modificações da definição do limite. Na definição do limite da direita, a desigualdade\(0<x−a<δ\) substitui\(0<|x−a|<δ\), o que garante que consideremos apenas valores\(x\) que sejam maiores que (à direita de)\(a\). Da mesma forma, na definição do limite da esquerda, a desigualdade\(−δ<x−a<0\) substitui\(0<|x−a|<δ\), o que garante que consideremos apenas valores menores que (à esquerda de)\(a\).\(x\)
Limite da direita:\(f(x)\) Seja definido em um intervalo aberto do formulário\((a,b)\) em que\(a<b\). Então
\[\lim_{x→a^+}f(x)=L \nonumber \]
se para cada um\(ε>0\), existe um\(δ>0\), tal que se\(0<x−a<δ\), então\(|f(x)−L|<ε\).
Limite da esquerda:\(f(x)\) Seja definido em um intervalo aberto do formulário\((b,c)\) onde\(b<c\). Então,
\[\lim_{x→c^−}f(x)=L \nonumber \]
se para cada um\(ε>0\),\(δ>0\) existe um se\( −δ<x−c<0\), então\(|f(x)−L|<ε\).
Prove isso
\[\lim_{x→4^+}\sqrt{x−4}=0.\nonumber \]
Solução
Deixe\(ε>0\).
Escolha\(δ=ε^2\). Como, em última análise\(∣\sqrt{x−4}−0∣<ε\), queremos, manipulamos essa desigualdade para obter\(\sqrt{x−4}<ε\) ou, equivalentemente\(0<x−4<ε^2\), fazer\(δ=ε^2\) uma escolha clara. Também podemos determinar\(δ\) geometricamente, conforme mostrado na Figura\(\PageIndex{4}\).
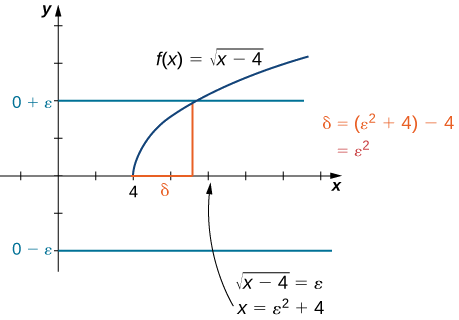
Suponha\(0<x−4<δ\). Assim,\(0<x−4<ε^2\). Conseqüentemente,\(0<\sqrt{x−4}<ε\). Finalmente,\(\left|\sqrt{x−4}−0\right|<ε\). Portanto,\(\displaystyle \lim_{x→4^+}\sqrt{x−4}=0\).
Encontre o\(δ\) correspondente\(ε\) para obter uma prova de que\(\displaystyle \lim_{x→1^−}\sqrt{1−x}=0\).
- Dica
-
Esboce o gráfico e use o Example\(\PageIndex{6}\) como guia de solução.
- Responda
-
\(δ=ε^2\)
Limites infinitos
Concluímos o processo de converter nossas ideias intuitivas de vários tipos de limites em definições formais rigorosas, buscando uma definição formal de limites infinitos. Para isso\(\displaystyle \lim_{x→a}f(x)=+∞\), queremos que os valores da função fiquem cada vez maiores\(f(x)\) à medida que\(x\) se aproxima\(a\). Em vez da exigência de que\(|f(x)−L|<ε\) para pequenos\(ε\) arbitrários e pequenos o suficiente\(δ\), queremos\(f(x)>M\) um positivo arbitrariamente grande\(M\) quando\(0<|x−a|<δ\) para pequeno o suficiente\(δ\).\(0<|x−a|<δ\) \(\PageIndex{5}\)A figura ilustra essa ideia mostrando o valor de\(δ\) para valores sucessivamente maiores de\(M\).
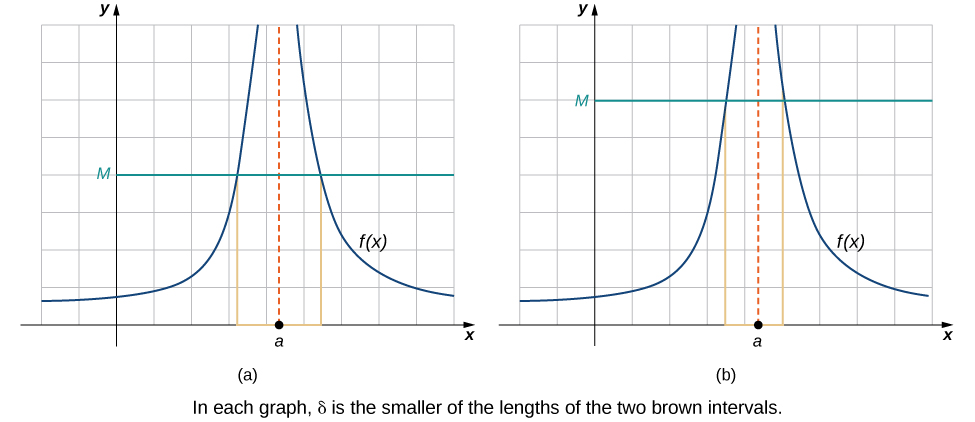
Figura\(\PageIndex{5}\): Esses gráficos traçam valores de\(δ\) for\(M\) para mostrar isso\(\displaystyle \lim_{x→a}f(x)=+∞\).
Deixe\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have an infinite limit
\[\lim_{x→a}f(x)=+∞ \nonumber \]
se para cada\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)>M\).
Deixe\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have a negative infinite limit
\[\lim_{x→a}f(x)=−∞ \nonumber \]
se para cada\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)<−M\).
Prove isso\(\displaystyle \lim_{x→3}\frac{1}{(x-3)^2}=\infty.\)
Solução
Usamos uma abordagem muito semelhante à nossa estratégia anterior de resolução de problemas. Primeiro, encontramos um apropriado\(δ>0\). Em seguida, escrevemos nossa prova.
Etapa 1: Primeiro, encontramos um apropriado\(δ>0\).
1. \(M\)Seja qualquer número real como esse\(M>0\).
2. Deixe\(f(x) = \dfrac{1}{(x-3)^2} > M\). Em seguida, resolvemos a expressão\(x - 3\).
Multiplicar os dois lados da desigualdade pela quantidade positiva\((x - 3)^2\) e dividir os dois lados pela quantidade positiva nos\(M\) dá:
\[ \frac{1}{M} > (x-3)^2 \nonumber \]
Tomando a raiz quadrada de ambos os lados, temos,
\[ \sqrt{\frac{1}{M}} > |x - 3|. \qquad \quad\left(\text{Remember that }\sqrt{x^2} = |x|.\right)\nonumber \]
Reescrever esta declaração nos dá,\(0 < |x-3| < \sqrt{\dfrac{1}{M}}\). A partir disso, nós escolhemos\(δ = \sqrt{\dfrac{1}{M}}\).
Etapa 2: Agora escrevemos uma prova.
3. Deixe\(δ = \sqrt{\dfrac{1}{M}}\) e assuma\(0 < |x-3| < δ = \sqrt{\dfrac{1}{M}}\).
Assim,
\[ |x-3| < \sqrt{\frac{1}{M}}. \nonumber \]
Quadrar os dois lados nos dá,
\[ (x-3)^2 < \frac{1}{M}. \nonumber \]
Tomando a recíproca de ambos os lados (e lembrando que isso inverterá a direção da desigualdade),
\[ \dfrac{1}{(x-3)^2} > M. \nonumber \]
Portanto, provamos que
\[\lim_{x→3}\frac{1}{(x-3)^2}=\infty.\nonumber \]
Uma prova muito semelhante será necessária para um limite igual\(-\infty\) a.
Observe que uma abordagem de limite unilateral geralmente precisará ser adotada com esse tipo de limite. Por exemplo, para provar:\(\displaystyle \lim_{x\to 0^+}\frac{1}{x} = \infty\).
Conceitos-chave
- A noção intuitiva de limite pode ser convertida em uma definição matemática rigorosa conhecida como definição épsilon-delta do limite.
- A definição de épsilon-delta pode ser usada para provar afirmações sobre limites.
- A definição épsilon-delta de um limite pode ser modificada para definir limites unilaterais.
- Uma definição similar de limite infinito pode ser usada para provar afirmações sobre limites infinitos.
Glossário
- definição do limite épsilon-delta
- \(\displaystyle \lim_{x→a}f(x)=L\)se para todos\(ε>0\), existe um\(δ>0\) tal que se\(0<|x−a|<δ\), então\(|f(x)−L|<ε\)
- desigualdade triangular
- Se\(a\) e\(b\) forem números reais, então\(|a+b|≤|a|+|b|\)
- definição formal de um limite infinito
- \(\displaystyle \lim_{x→a}f(x)=\infty\)se para cada um\(M>0\), existe um\(δ>0\) tal que se\(0<|x−a|<δ\), então,\(f(x)>M\)
\(\displaystyle \lim_{x→a}f(x)=-\infty\) se para todos\(M>0\), existe um\(δ>0\) tal que se\(0<|x−a|<δ\), então\(f(x)<-M\)
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College), added Example \(\PageIndex{7}\) and entries for infinite limits under Key Concepts and the Glossary.


