2.2: O limite de uma função
- Page ID
- 188674
- Usando a notação correta, descreva o limite de uma função.
- Use uma tabela de valores para estimar o limite de uma função ou identificar quando o limite não existe.
- Use um gráfico para estimar o limite de uma função ou identificar quando o limite não existe.
- Defina limites unilaterais e forneça exemplos.
- Explique a relação entre limites unilaterais e bilaterais.
- Usando a notação correta, descreva um limite infinito.
- Defina uma assíntota vertical.
O conceito de um processo limite ou limitador, essencial para a compreensão do cálculo, existe há milhares de anos. Na verdade, os primeiros matemáticos usaram um processo limitante para obter aproximações cada vez melhores das áreas dos círculos. No entanto, a definição formal de limite — como a conhecemos e entendemos hoje — não apareceu até o final do século XIX. Portanto, começamos nossa busca para entender os limites, como fizeram nossos ancestrais matemáticos, usando uma abordagem intuitiva. No final deste capítulo, munidos de uma compreensão conceitual dos limites, examinamos a definição formal de um limite.
Começamos nossa exploração dos limites dando uma olhada nos gráficos das funções
- \(f(x)=\dfrac{x^2−4}{x−2}\),
- \(g(x)=\dfrac{|x−2|}{x−2}\), e
- \(h(x)=\dfrac{1}{(x−2)^2}\),
que são mostrados na Figura\(\PageIndex{1}\). Em particular, vamos focar nossa atenção no comportamento de cada gráfico ao redor e ao redor dele\(x=2\).
Cada uma das três funções é indefinida em\(x=2\), mas se fizermos essa afirmação e nenhuma outra, daremos uma imagem muito incompleta de como cada função se comporta nas proximidades de\(x=2\). Para expressar o comportamento de cada gráfico nas proximidades de uma forma\(2\) mais completa, precisamos introduzir o conceito de limite.
Definição intuitiva de um limite
Vamos primeiro examinar mais de perto como a função\(f(x)=(x^2−4)/(x−2)\) se comporta\(x=2\) na Figura\(\PageIndex{1}\). Como os valores da\(x\) abordagem\(2\) de ambos os lados\(2\), os valores da\(y=f(x)\) abordagem\(4\). Matematicamente, dizemos que o limite de\(f(x)\) as\(x\) aproximações\(2\) é\(4\). Simbolicamente, expressamos esse limite como
\(\displaystyle \lim_{x \to 2} f(x)=4\).
A partir dessa breve análise informal de um limite, vamos começar a desenvolver uma definição intuitiva do limite. Podemos pensar no limite de uma função em um número\(a\) como sendo o único número real\(L\) que os valores funcionais abordam como a abordagem de\(x\) valores\(a\) -, desde que esse número real\(L\) exista. Dito com mais cuidado, temos a seguinte definição:
\(f(x)\)Seja uma função definida em todos os valores em um intervalo aberto contendo\(a\), com a possível exceção de\(a\) si mesma, e\(L\) seja um número real. Se todos os valores da função se\(f(x)\) aproximam do número real\(L\) como os valores de se\(x(≠a)\) aproximam do número\(a\), então dizemos que o limite de\(f(x)\) as\(x\) se aproxima\(a\) é\(L\). (Mais sucinto, à medida\(x\) que se aproxima\(a\),\(f(x)\) se aproxima e fica próximo\(L\).) Simbolicamente, expressamos essa ideia como
\[\lim_{x \to a} f(x)=L. \label{limit} \]
Podemos estimar limites construindo tabelas de valores funcionais e observando seus gráficos. Esse processo é descrito na seguinte Estratégia de Solução de Problemas.
1. Para avaliar\(\displaystyle \lim_{x \to a} f(x)\), começamos preenchendo uma tabela de valores funcionais. Devemos escolher dois conjuntos de\(x\) valores -— um conjunto de valores próximos\(a\) e menores que\(a\), e outro conjunto de valores próximos\(a\) e maiores que\(a\). A tabela\(\PageIndex{1}\) demonstra a aparência de suas tabelas.
| \(x\) | \(f(x)\) | \(x\) | \(f(x)\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">\(a-0.1\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a-0.1)\) | \ (x\)” style="text-align:center; ">\(a+0.1\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a+0.1)\) |
| \ (x\)” style="text-align:center; ">\(a-0.01\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a-0.01)\) | \ (x\)” style="text-align:center; ">\(a+0.01\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a+0.01)\) |
| \ (x\)” style="text-align:center; ">\(a-0.001\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a-0.001)\) | \ (x\)” style="text-align:center; ">\(a+0.001\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a+0.001)\) |
| \ (x\)” style="text-align:center; ">\(a-0.0001\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a-0.0001)\) | \ (x\)” style="text-align:center; ">\(a+0.0001\) | \ (f (x)\)” style="alinhamento do texto: centro; ">\(f(a+0.0001)\) |
| \ (f (x)\)” rowspan="1" style="text-align:center; ">Use valores adicionais conforme necessário. | \ (f (x)\)” rowspan="1" style="text-align:center; ">Use valores adicionais conforme necessário. | ||
2. Em seguida, vamos examinar os valores em cada uma das\(f(x)\) colunas e determinar se os valores parecem estar se aproximando de um único valor à medida que avançamos para baixo em cada coluna. Em nossas colunas, examinamos a sequência\(f(a−0.1)\),\(f(a−0.01)\),\(f(a−0.001)\)\(f(a−0.0001)\), e assim por diante\(f(a+0.1), \;f(a+0.01), \;f(a+0.001), \;f(a+0.0001)\), e assim por diante. (Nota: Embora tenhamos escolhido os\(x\) valores\(a±0.1, \;a±0.01, \;a±0.001, \;a±0.0001\) -e assim por diante, e esses valores provavelmente funcionarão quase todas as vezes, em raras ocasiões, talvez precisemos modificar nossas escolhas.)
3. Se ambas as colunas se aproximarem\(y\) de um valor comum\(L\), afirmamos\(\displaystyle \lim_{x \to a}f(x)=L\). Podemos usar a estratégia a seguir para confirmar o resultado obtido na tabela ou como um método alternativo para estimar um limite.
4. Usando uma calculadora gráfica ou um software de computador que nos permite representar graficamente funções, podemos traçar a função\(f(x)\), garantindo que os valores funcionais de\(f(x)\) for\(x\) -values near\(a\) estejam em nossa janela. Podemos usar o recurso de rastreamento para percorrer o gráfico da função e observar a leitura do\(y\) valor -à medida que os\(x\) valores -se aproximam\(a\). Se os\(y\) valores -se aproximam\(L\) como nossos\(x\) valores -se aproximam\(a\) de ambas as direções, então\(\displaystyle \lim_{x \to a}f(x)=L\). Talvez precisemos ampliar nosso gráfico e repetir esse processo várias vezes.
Aplicamos essa estratégia de resolução de problemas para calcular um limite nos exemplos\(\PageIndex{1A}\)\(\PageIndex{1B}\) e.
Avalie\(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) usando uma tabela de valores funcionais.
Solução
Calculamos os valores de\(f(x)=\dfrac{\sin x}{x}\) para os valores\(x\) listados na Tabela\(\PageIndex{2}\).
| \(x\) | \(\frac{\sin x}{x}\) | \(x\) | \(\frac{\sin x}{x}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.998334166468 | \ (x\)” style="text-align:center; ">0.1 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.998334166468 |
| \ (x\)” style="text-align:center; ">-0,01 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999983333417 | \ (x\)” style="text-align:center; ">0,01 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999983333417 |
| \ (x\)” style="text-align:center; ">-0,001 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999999833333 | \ (x\)” style="text-align:center; ">0.001 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999999833333 |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0,999999998333 | \ (x\)” style="text-align:center; ">0.0001 | \ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0,999999998333 |
Nota: Os valores nesta tabela foram obtidos usando uma calculadora e usando todos os lugares fornecidos na saída da calculadora.
Ao lermos cada\(\dfrac{\sin x}{x}\) coluna, vemos que os valores em cada coluna parecem estar se aproximando de um. Portanto, é bastante razoável concluir isso\(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). Um gráfico gerado por calculadora ou computador de\(f(x)=\dfrac{\sin x}{x}\) seria semelhante ao mostrado na Figura\(\PageIndex{2}\) e confirma nossa estimativa.
![Um gráfico de f (x) = sin (x) /x no intervalo [-6, 6]. A função curva tem um intercepto y em x=0 e x intercepta em y=pi e y=-pi.](https://math.libretexts.org/@api/deki/files/7963/imageedit_1_8651812985.png)
Avalie\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) usando uma tabela de valores funcionais.
Solução
Como antes, usamos uma tabela — neste caso, Tabela\(\PageIndex{3}\) — para listar os valores da função para os valores fornecidos de\(x\).
| \(x\) | \(\frac{\sqrt{x}−2}{x−4}\) | \(x\) | \(\frac{\sqrt{x}−2}{x−4}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">3.9 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0,251582341869 | \ (x\)” style="text-align:center; ">4.1 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.248456731317 |
| \ (x\)” style="text-align:center; ">3,99 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0,25015644562 | \ (x\)” style="text-align:center; ">4.01 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.24984394501 |
| \ (x\)” style="text-align:center; ">3.999 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.250015627 | \ (x\)” style="text-align:center; ">4.001 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.249984377 |
| \ (x\)” style="text-align:center; ">3.9999 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0,250001563 | \ (x\)” style="text-align:center; ">4.0001 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.249998438 |
| \ (x\)” style="text-align:center; ">3.99999 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0,25000016 | \ (x\)” style="text-align:center; ">4.00001 | \ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.24999984 |
Depois de inspecionar esta tabela, vemos que os valores funcionais menores que 4 parecem estar diminuindo para 0,25, enquanto os valores funcionais maiores que 4 parecem estar aumentando em direção a 0,25. Concluímos isso\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0.25\). Confirmamos essa estimativa usando o gráfico\(f(x)=\dfrac{\sqrt{x}−2}{x−4}\) mostrado na Figura\(\PageIndex{3}\).
![Um gráfico da função f (x) = (sqrt (x) — 2)/(x-4) no intervalo [0,8]. Há um círculo aberto na função em x=4. A função se curva assintoticamente em direção ao eixo x e ao eixo y no quadrante um.](https://math.libretexts.org/@api/deki/files/7964/imageedit_5_9266726966.png)
Faça uma estimativa\(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) usando uma tabela de valores funcionais. Use um gráfico para confirmar sua estimativa.
- Dica
-
Use 0,9, 0,99, 0,999, 0,9999, 0,99999 e 1,1, 1,01, 1,001, 1,0001, 1,00001 como seus valores de tabela.
- Responda
-
\[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]
Neste ponto, vemos em Exemplos\(\PageIndex{1A}\) e\(\PageIndex{1b}\) que pode ser tão fácil, se não mais fácil, estimar um limite de uma função inspecionando seu gráfico quanto estimar o limite usando uma tabela de valores funcionais. No exemplo\(\PageIndex{2}\), avaliamos um limite exclusivamente observando um gráfico em vez de usar uma tabela de valores funcionais.
Conforme\(g(x)\) mostrado na Figura\(\PageIndex{4}\), avalie\(\displaystyle \lim_{x\to−1}g(x)\).
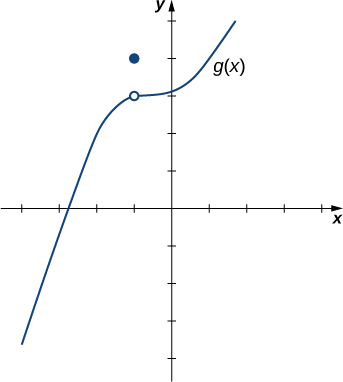
Solução:
Apesar do fato de que\(g(−1)=4\), à medida que\(x\) os valores -se aproximam\(−1\) de ambos os lados, os\(g(x)\) valores se aproximam\(3\). Portanto,\(\displaystyle \lim_{x\to−1}g(x)=3\). Observe que podemos determinar esse limite sem sequer conhecer a expressão algébrica da função.
Com base no exemplo\(\PageIndex{2}\), fazemos a seguinte observação: É possível que o limite de uma função exista em um ponto e que a função seja definida nesse ponto, mas o limite da função e o valor da função no ponto podem ser diferentes.
Use o gráfico de\(h(x)\) na Figura\(\PageIndex{5}\) para avaliar\(\displaystyle \lim_{x \to 2}h(x)\), se possível.
![Um gráfico da função h (x), que é uma parábola representada graficamente sobre [-2,5, 5]. Há um círculo aberto onde o vértice deve estar no ponto (2, -1).](https://math.libretexts.org/@api/deki/files/7966/imageedit_13_2727890618.png)
- Dica
-
Qual\(y\) valor a função aborda como a abordagem\(x\) de -valores\(2\)?
- Solução
-
\(\displaystyle \lim_{x \to 2}h(x)=−1.\)
Examinar uma tabela de valores funcionais ou observar o gráfico de uma função nos fornece uma visão útil sobre o valor do limite de uma função em um determinado ponto. No entanto, essas técnicas dependem demais de suposições. Eventualmente, precisamos desenvolver métodos alternativos de avaliação de limites. Esses novos métodos são de natureza mais algébrica e os exploraremos na próxima seção; no entanto, neste momento, introduzimos dois limites especiais que são fundamentais para as técnicas futuras.
\(a\)Seja um número real e\(c\) uma constante.
- \(\displaystyle \lim_{x \to a}x=a\)
- \(\displaystyle \lim_{x \to a}c=c\)
Podemos fazer as seguintes observações sobre esses dois limites.
- Para o primeiro limite, observe que, à medida que\(x\) se aproxima\(a\), o mesmo acontece\(f(x)\), porque\(f(x)=x\). Consequentemente,\(\displaystyle \lim_{x \to a}x=a\).
- Para o segundo limite, considere a Tabela\(\PageIndex{4}\).
| \(x\) | \(f(x)=c\) | \(x\) | \(f(x)=c\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">\(a-0.1\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) | \ (x\)” style="text-align:center; ">\(a+0.1\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) |
| \ (x\)” style="text-align:center; ">\(a-0.01\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) | \ (x\)” style="text-align:center; ">\(a+0.01\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) |
| \ (x\)” style="text-align:center; ">\(a-0.001\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) | \ (x\)” style="text-align:center; ">\(a+0.001\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) |
| \ (x\)” style="text-align:center; ">\(a-0.0001\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) | \ (x\)” style="text-align:center; ">\(a+0.0001\) | \ (f (x) =c\)” style="alinhamento do texto: centro; ">\(c\) |
Observe que para todos os valores de\(x\) (independentemente de estarem se aproximando\(a\)), os valores\(f(x)\) permanecem constantes em\(c\). Não temos escolha a não ser concluir\(\displaystyle \lim_{x \to a}c=c\).
A existência de um limite
Ao considerarmos o limite no próximo exemplo, lembre-se de que, para que o limite de uma função exista em um ponto, os valores funcionais devem se aproximar de um único valor de número real nesse ponto. Se os valores funcionais não se aproximarem de um único valor, o limite não existe.
Avalie\(\displaystyle\lim_{x \to 0}\sin(1/x)\) usando uma tabela de valores.
Solução
A tabela\(\PageIndex{5}\) lista os valores da função\(\sin(1/x)\) para os valores fornecidos de\(x\).
| \(x\) | \(\sin(1/x)\) | \(x\) | \(\sin(1/x)\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ sin (1/x)\)” style="alinhamento do texto: centro; ">0,544021110889 | \ (x\)” style="text-align:center; ">0.1 | \ (\ sin (1/x)\)” style="text-align:center; ">−0.544021110889 |
| \ (x\)” style="text-align:center; ">-0,01 | \ (\ sin (1/x)\)” style="alinhamento do texto: centro; ">0,50636564111 | \ (x\)” style="text-align:center; ">0,01 | \ (\ sin (1/x)\)” style="text-align:center; ">−0.50636564111 |
| \ (x\)” style="text-align:center; ">-0,001 | \ (\ sin (1/x)\)” style="text-align:center; ">−0.8268795405312 | \ (x\)” style="text-align:center; ">0.001 | \ (\ sin (1/x)\)” style="alinhamento de texto: centro; ">0,8268795405312 |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ sin (1/x)\)” style="alinhamento do texto: centro; ">0,305614388888 | \ (x\)” style="text-align:center; ">0.0001 | \ (\ sin (1/x)\)” style="text-align:center; ">−0.305614388888 |
| \ (x\)” style="text-align:center; ">-0.00001 | \ (\ sin (1/x)\)” style="text-align:center; ">−0.035748797987 | \ (x\)” style="text-align:center; ">0.00001 | \ (\ sin (1/x)\)” style="alinhamento do texto: centro; ">0,035748797987 |
| \ (x\)” style="text-align:center; ">-0.000001 | \ (\ sin (1/x)\)” style="alinhamento do texto: centro; ">0,349993504187 | \ (x\)” style="text-align:center; ">0.000001 | \ (\ sin (1/x)\)” style="alinhamento de texto: centro; ">−0,349993504187 |
Depois de examinar a tabela de valores funcionais, podemos ver que os\(y\) valores -não parecem se aproximar de um único valor. Parece que o limite não existe. Antes de tirar essa conclusão, vamos adotar uma abordagem mais sistemática. Considere a seguinte sequência de\(x\) valores -aproximada\(0\):
\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac{2}{9π},\;\frac{2}{11π},\;….\nonumber \]
Os\(y\) valores -correspondentes são
\[1,\;-1,\;1,\;-1,\;1,\;-1,\;....\nonumber \]
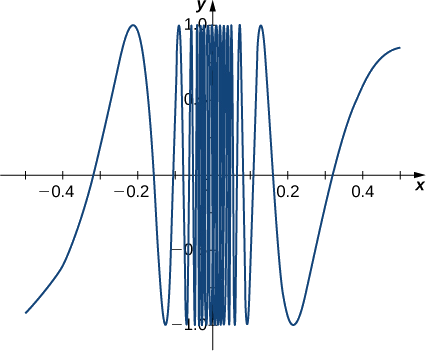
Neste ponto, podemos realmente concluir que isso\(\displaystyle \lim_{x \to 0} \sin(1/x)\) não existe. (Os matemáticos frequentemente abreviam “não existe” como DNE. Assim, escreveríamos\(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) O gráfico de\(f(x)=\sin(1/x)\) é mostrado na Figura\(\PageIndex{6}\) e fornece uma imagem mais clara do comportamento das\(\sin(1/x)\)\(x\) abordagens\(0\). Você pode ver que\(\sin(1/x)\) oscila cada vez mais intensamente entre\(−1\) e à\(1\) medida que\(x\) se aproxima\(0\).
Use uma tabela de valores funcionais para avaliar\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\), se possível.
- Dica
-
Use\(x\) -values 1,9, 1,99, 1,999, 1,9999, 1,99999 e 2,1, 2,01, 2,001, 2,0001, 2,00001 em sua tabela.
- Responda
-
\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\)não existe.
Limites unilaterais
Às vezes, indicar que o limite de uma função não existe em um ponto não nos fornece informações suficientes sobre o comportamento da função naquele ponto específico. Para ver isso, agora revisitamos a função\(g(x)=|x−2|/(x−2)\) introduzida no início da seção (veja a Figura\(\PageIndex{1}\) (b)). Quando escolhemos valores\(x\) próximos a\(2\),\(g(x)\) não se aproxima de um único valor, então o limite como\(x\) abordagens\(2\) não existe, ou seja,\(\displaystyle \lim_{x \to 2}g(x)\) DNE. No entanto, essa afirmação por si só não nos dá uma visão completa do comportamento da função em torno do\(x\) valor\(2\). Para fornecer uma descrição mais precisa, introduzimos a ideia de um limite unilateral. Para todos os valores à esquerda de\(2\) (ou ao lado negativo de\(2\)),\(g(x)=−1\). Assim, à medida que\(x\) se aproxima\(2\) da esquerda,\(g(x)\) se aproxima\(−1\). Matematicamente, dizemos que o limite à medida que\(x\) se aproxima\(2\) da esquerda é\(−1\). Simbolicamente, expressamos essa ideia como
\[\lim_{x \to 2^−}g(x)=−1. \nonumber \]
Da mesma forma, à medida que\(x\) se\(2\) aproxima da direita (ou do lado positivo),\(g(x)\) se aproxima\(1\). Simbolicamente, expressamos essa ideia como
\[\lim_{x \to 2^+}g(x)=1.\nonumber \]
Agora podemos apresentar uma definição informal de limites unilaterais.
Definimos dois tipos de limites unilaterais.
Limite a partir da esquerda:
\(f(x)\)Seja uma função definida em todos os valores em um intervalo aberto do formulário\((z,a)\) e\(L\) seja um número real. Se os valores da função se\(f(x)\) aproximam do número real à\(L\) medida que os valores de\(x\) (onde\(x<a\)) se aproximam do número\(a\), então dizemos que esse\(L\) é o limite de\(f(x)\) quando\(x\) se aproxima\(a\) da esquerda. Simbolicamente, expressamos essa ideia como
\[\lim_{x \to a^−}f(x)=L. \nonumber \]
Limite a partir da direita:
\(f(x)\)Seja uma função definida em todos os valores em um intervalo aberto do formulário\((a,c)\) e\(L\) seja um número real. Se os valores da função se\(f(x)\) aproximam do número real à\(L\) medida que os valores de\(x\) (onde\(x>a\)) se aproximam do número\(a\), então dizemos que esse\(L\) é o limite de\(f(x)\) quando\(x\) se aproxima\(a\) da direita. Simbolicamente, expressamos essa ideia como
\[\lim_{x \to a^+}f(x)=L. \nonumber \]
Para a função\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\), avalie cada um dos limites a seguir.
- \(\displaystyle \lim_{x \to 2^−}f(x)\)
- \(\displaystyle \lim_{x \to 2^+}f(x)\)
Solução
Podemos usar tabelas de valores funcionais novamente. Observe na Tabela\(\PageIndex{6}\) que para valores\(x\) menores que\(2\), usamos\(f(x)=x+1\) e para valores\(x\) maiores que\(2\), usamos\(f(x)=x^2−4.\)
| \(x\) | \(f(x)=x+1\) | \(x\) | \(f(x)=x^2-4\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">1.9 | \ (f (x) =x+1\)” style="alinhamento do texto: centro; ">2.9 | \ (x\)” style="text-align:center; ">2.1 | \ (f (x) =x^2-4\)” style="alinhamento do texto: centro; ">0,41 |
| \ (x\)” style="text-align:center; ">1,99 | \ (f (x) =x+1\)” style="alinhamento do texto: centro; ">2,99 | \ (x\)” style="text-align:center; ">2.01 | \ (f (x) =x^2-4\)” style="alinhamento do texto: centro; ">0.0401 |
| \ (x\)” style="text-align:center; ">1.999 | \ (f (x) =x+1\)” style="alinhamento do texto: centro; ">2.999 | \ (x\)” style="text-align:center; ">2.001 | \ (f (x) =x^2-4\)” style="alinhamento do texto: centro; ">0.004001 |
| \ (x\)” style="text-align:center; ">1.9999 | \ (f (x) =x+1\)” style="alinhamento do texto: centro; ">2.9999 | \ (x\)” style="text-align:center; ">2.0001 | \ (f (x) =x^2-4\)” style="alinhamento do texto: centro; ">0,00040001 |
| \ (x\)” style="text-align:center; ">1.99999 | \ (f (x) =x+1\)” style="alinhamento do texto: centro; ">2.99999 | \ (x\)” style="text-align:center; ">2.00001 | \ (f (x) =x^2-4\)” style="alinhamento do texto: centro; ">0,0000400001 |
Com base nessa tabela, podemos concluir que a.\(\displaystyle \lim_{x \to 2^−}f(x)=3\) e\(\displaystyle \lim_{x \to 2^+}f(x)=0\) b. Portanto, o limite (bilateral) de\(f(x)\) não existe em\(x=2\). A figura\(\PageIndex{7}\) mostra um gráfico\(f(x)\) e reforça nossa conclusão sobre esses limites.
Use uma tabela de valores funcionais para estimar os seguintes limites, se possível.
- \(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\)
- \(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}\)
- Dica
-
Use\(x\) -valores 1,9, 1,99, 1,999, 1,9999, 1,99999 para estimar\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\).
Use\(x\) os valores -2.1, 2.01, 2.001, 2.0001, 2.00001 para estimar\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.\)
(Essas tabelas estão disponíveis em um problema anterior do Checkpoint.)
- Solução a
-
uma.\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4\)
- Solução b
-
\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4\)
Vamos agora considerar a relação entre o limite de uma função em um ponto e os limites da direita e da esquerda nesse ponto. Parece claro que, se o limite da direita e o limite da esquerda tiverem um valor comum, esse valor comum será o limite da função nesse ponto. Da mesma forma, se o limite da esquerda e o limite da direita assumirem valores diferentes, o limite da função não existirá. Essas conclusões estão resumidas na Nota.
\(f(x)\)Seja uma função definida em todos os valores em um intervalo aberto contendo\(a\), com a possível exceção de\(a\) si mesma, e\(L\) seja um número real. Em seguida,
\[\lim_{x \to a}f(x)=L \nonumber \]
se e somente se\(\displaystyle \lim_{x \to a^−}f(x)=L\)\(\displaystyle \lim_{x \to a^+} f(x)=L\) e.
Limites infinitos
Avaliar o limite de uma função em um ponto ou avaliar o limite de uma função da direita e da esquerda em um ponto nos ajuda a caracterizar o comportamento de uma função em torno de um determinado valor. Como veremos, também podemos descrever o comportamento de funções que não têm limites finitos.
Agora voltamos nossa atenção para\(h(x)=1/(x−2)^2\) a terceira e última função introduzida no início desta seção (veja a Figura\(\PageIndex{1}\) (c)). Em seu gráfico, vemos que, como valores de\(x\) abordagem\(2\), os valores de\(h(x)=1/(x−2)^2\) se tornam cada vez maiores e, de fato, se tornam infinitos. Matematicamente, dizemos que o limite de\(h(x)\) as\(x\) aproximações\(2\) é o infinito positivo. Simbolicamente, expressamos essa ideia como
\[\lim_{x \to 2}h(x)=+∞. \nonumber \]
De forma mais geral, definimos limites infinitos da seguinte forma:
Definimos três tipos de limites infinitos.
Limites infinitos da esquerda:\(f(x)\) Seja uma função definida em todos os valores em um intervalo aberto do formulário\((b,a)\).
i. Se os valores de\(f(x)\) aumentam sem limite à medida que os valores de\(x\) (onde\(x<a\)) se aproximam do número\(a\), então dizemos que o limite quando\(x\) se aproxima\(a\) da esquerda é infinito positivo e escrevemos\[\lim_{x \to a^−}f(x)=+∞. \nonumber \]
ii. Se os valores de\(f(x)\) diminuem sem limite à medida que os valores de\(x\) (onde\(x<a\)) se aproximam do número\(a\), então dizemos que o limite quando\(x\) se aproxima\(a\) da esquerda é menos infinito e escrevemos\[\lim_{x \to a^−}f(x)=−∞. \nonumber \]
Limites infinitos da direita:\(f(x)\) Seja uma função definida em todos os valores em um intervalo aberto do formulário\((a,c)\).
i. Se os valores de\(f(x)\) aumentam sem limite à medida que os valores de\(x\) (onde\(x>a\)) se aproximam do número\(a\), então dizemos que o limite quando\(x\) se aproxima\(a\) da direita é infinito positivo e escrevemos\[\lim_{x \to a^+}f(x)=+∞. \nonumber \]
ii. Se os valores de\(f(x)\) diminuem sem limite à medida que os valores de\(x\) (onde\(x>a\)) se aproximam do número\(a\), então dizemos que o limite quando\(x\) se aproxima\(a\) da direita é menos infinito e escrevemos\[\lim_{x \to a^+}f(x)=−∞. \nonumber \]
Limite infinito bilateral:\(f(x)\) Seja definido para todos\(x≠a\) em um intervalo aberto contendo\(a\)
i. Se os valores de\(f(x)\) aumentam sem limite à medida que os valores de\(x\) (onde\(x≠a\)) se aproximam do número\(a\), então dizemos que o limite à medida que\(x\) se aproxima\(a\) é infinito positivo e escrevemos\[\lim_{x \to a} f(x)=+∞. \nonumber \]
ii. Se os valores de\(f(x)\) diminuem sem limite à medida que os valores de\(x\) (onde\(x≠a\)) se aproximam do número\(a\), então dizemos que o limite à medida que\(x\) se aproxima\(a\) é menos infinito e escrevemos\[\lim_{x \to a}f(x)=−∞. \nonumber \]
É importante entender que, quando escrevemos declarações como\(\displaystyle \lim_{x \to a}f(x)=+∞\) ou\(\displaystyle \lim_{x \to a}f(x)=−∞\) descrevemos o comportamento da função, como acabamos de defini-la. Não estamos afirmando que existe um limite. Para que o limite de uma função\(f(x)\) exista em\(a\), ela deve se aproximar de um número real\(L\) conforme\(x\) se aproxima\(a\). Dito isso, se, por exemplo\(\displaystyle \lim_{x \to a}f(x)=+∞\), sempre escrevermos\(\displaystyle \lim_{x \to a}f(x)=+∞\) em vez de\(\displaystyle \lim_{x \to a}f(x)\) DNE.
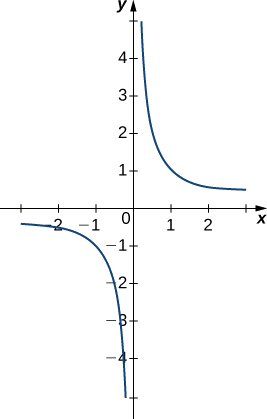
Avalie cada um dos seguintes limites, se possível. Use uma tabela de valores funcionais e um gráfico\(f(x)=1/x\) para confirmar sua conclusão.
- \(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
- \(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
- \( \displaystyle \lim_{x \to 0}\frac{1}{x}\)
Solução
Comece construindo uma tabela de valores funcionais.
| \(x\) | \(\dfrac{1}{x}\) | \(x\) | \(\dfrac{1}{x}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-10 | \ (x\)” style="text-align:center; ">0.1 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">10 |
| \ (x\)” style="text-align:center; ">-0,01 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-100 | \ (x\)” style="text-align:center; ">0,01 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">100 |
| \ (x\)” style="text-align:center; ">-0,001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-1000 | \ (x\)” style="text-align:center; ">0.001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">1000 |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-10.000 | \ (x\)” style="text-align:center; ">0.0001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">10.000 |
| \ (x\)” style="text-align:center; ">-0.00001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-100.000 | \ (x\)” style="text-align:center; ">0.00001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">100.000 |
| \ (x\)” style="text-align:center; ">-0.000001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">-1.000.000 | \ (x\)” style="text-align:center; ">0.000001 | \ (\ dfrac {1} {x}\)” style="text-align:center; ">1.000.000 |
a. Os valores de\(1/x\) diminuem sem limite à medida que\(x\) se\(0\) aproximam da esquerda. Concluímos que
\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber \]
b. Os valores de\(1/x\) aumentam sem limites à medida que\(x\) se\(0\) aproximam da direita. Concluímos que
\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber \]
c. Como\(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) e\(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) têm valores diferentes, concluímos que
\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber \]
O gráfico\(f(x)=1/x\) da Figura\(\PageIndex{8}\) confirma essas conclusões.
Avalie cada um dos seguintes limites, se possível. Use uma tabela de valores funcionais e um gráfico\(f(x)=1/x^2\) para confirmar sua conclusão.
- \(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)
Limites infinitos de números inteiros positivos
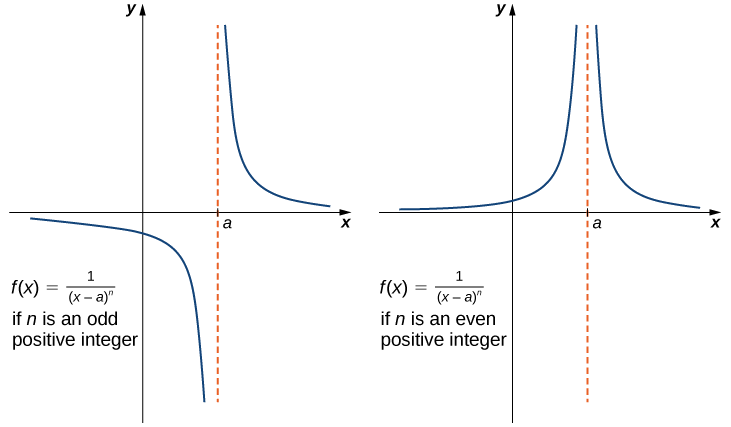
Se\(n\) for um número inteiro par positivo, então
\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1} \]
Se\(n\) for um número inteiro ímpar positivo, então
\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2} \]
e
\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3} \]
Também devemos ressaltar que, nos gráficos de\(f(x)=1/(x−a)^n\), pontos no gráfico com\(x\) coordenadas -muito próximas\(a\) estão muito próximos da linha vertical\(x=a\). Ou seja, à medida que\(x\) se aproxima\(a\), os pontos no gráfico de\(f(x)\) estão mais próximos da linha\(x=a\). A linha\(x=a\) é chamada de assíntota vertical do gráfico. Definimos formalmente uma assíntota vertical da seguinte forma:
\(f(x)\)Seja uma função. Se alguma das condições a seguir for válida, a linha\(x=a\) será uma assíntota vertical de\(f(x)\).
\[\lim_{x \to a^−}f(x)=+∞ \nonumber \]
\[\lim_{x \to a^−}f(x)=−∞ \nonumber \]
\[\lim_{x \to a^+}f(x)=+∞ \nonumber \]
\[\lim_{x \to a^+}f(x)=−∞ \nonumber \]
\[\lim_{x \to a}f(x)=+∞ \nonumber \]
\[\lim_{x \to a}f(x)=−∞ \nonumber \]
Avalie cada um dos seguintes limites usando as Equações\ ref {inFlim1},\ ref {inFlim2} e\ ref {inFlim3} acima. Identifique qualquer assíntota vertical da função\(f(x)=1/(x+3)^4.\)
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)
Solução
Podemos usar as equações acima diretamente.
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)
A função\(f(x)=1/(x+3)^4\) tem uma assíntota vertical de\(x=−3\).
Avalie cada um dos limites a seguir. Identifique qualquer assíntota vertical da função\(f(x)=\dfrac{1}{(x−2)^3}\).
- \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)
- Responda a
-
\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
- Resposta b
-
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
- Resposta c
-
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)DNE. A linha\(x=2\) é a assíntota vertical de\(f(x)=1/(x−2)^3.\)
No exemplo a seguir, colocamos nosso conhecimento de vários tipos de limites a serem usados para analisar o comportamento de uma função em vários pontos diferentes.
Use o gráfico de\(f(x)\) na Figura\(\PageIndex{10}\) para determinar cada um dos seguintes valores:
- \(\displaystyle \lim_{x \to −4^−}f(x)\);\(\displaystyle \lim_{x \to −4^+}f(x)\);\(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
- \(\displaystyle \lim_{x \to −2^−}f(x\))\(\displaystyle \lim_{x \to −2^+}f(x)\);\(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
- \( \displaystyle \lim_{x \to 1^−}f(x)\);\(\displaystyle \lim_{x \to 1^+}f(x)\);\(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
- \( \displaystyle \lim_{x \to 3^−}f(x)\);\(\displaystyle \lim_{x \to 3^+}f(x)\);\(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)
![O gráfico de uma função f (x) descrito pelos limites e valores acima. Há uma curva suave para valores abaixo de x=-2; em (-2, 3), há um círculo aberto. Há uma curva suave entre (-2, 1] com um círculo fechado em (1,6). Há um círculo aberto em (1,3) e uma curva suave que se estende de lá para baixo de forma assintotica até o infinito negativo ao longo de x=3. A função também se curva assintoticamente ao longo de x=3 do outro lado, também se estendendo até o infinito negativo. A função então muda a concavidade no primeiro quadrante em torno de y = 4,5 e continua subindo.](https://math.libretexts.org/@api/deki/files/7969/imageedit_30_9857663504.png)
Solução
Usando as definições acima e o gráfico como referência, chegamos aos seguintes valores:
- \(\displaystyle \lim_{x \to −4^−}f(x)=0\);\(\displaystyle \lim_{x \to −4^+}f(x)=0\);\(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
- \(\displaystyle \lim_{x \to −2^−}f(x)=3\);\(\displaystyle \lim_{x \to −2^+}f(x)=3\);\(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) é indefinido
- \(\displaystyle \lim_{x \to 1^−}f(x)=6\);\(\displaystyle \lim_{x \to 1^+}f(x)=3\);\(\displaystyle \lim_{x \to 1}f(x)\) DEN;\(f(1)=6\)
- \(\displaystyle \lim_{x \to 3^−}f(x)=−∞\);\(\displaystyle \lim_{x \to 3^+}f(x)=−∞\);\(\displaystyle \lim_{x \to 3}f(x)=−∞\);\(f(3)\) é indefinido
Avalie\(\displaystyle\lim_{x \to 1}f(x)\)\(f(x)\) como mostrado aqui:
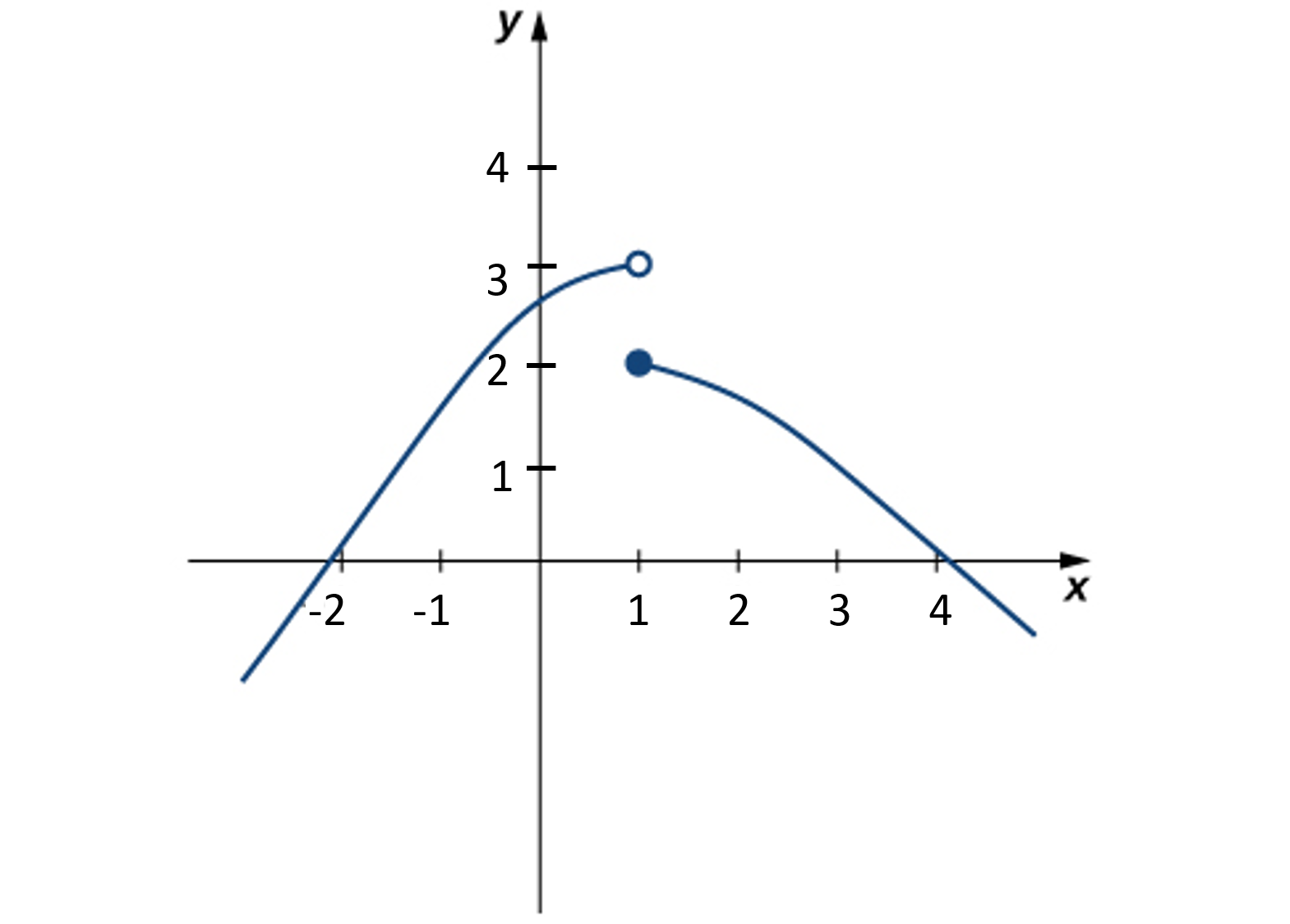
- Dica
-
Compare o limite da direita com o limite da esquerda.
- Responda
-
\(\displaystyle\lim_{x \to 1}f(x)\)não existe
Na abertura do capítulo, mencionamos brevemente como Albert Einstein mostrou que existe um limite para a velocidade com que qualquer objeto pode viajar. Dada a equação de Einstein para a massa de um objeto em movimento
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]
qual é o valor desse limite?

Solução
Nosso ponto de partida é a equação de Einstein para a massa de um objeto em movimento,
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]
onde\(m_0\) está a massa do objeto em repouso,\(v\) sua velocidade e\(c\) é a velocidade da luz. Para ver como a massa muda em altas velocidades, podemos representar graficamente a razão das\(m/m_0\) massas em função da razão das velocidades\(v/c\) (Figura\(\PageIndex{13}\)).
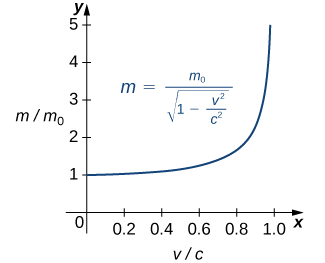
Podemos ver que, à medida que a proporção de velocidades se aproxima de 1, ou seja, à medida que a velocidade do objeto se aproxima da velocidade da luz, a proporção de massas aumenta sem limites. Em outras palavras, a função tem uma assíntota vertical em\(v/c=1\). Podemos tentar alguns valores dessa proporção para testar essa ideia.
| \(v/c\) | \(\sqrt{1-\frac{v^2}{c^2}}\) | \(m/m_o\) |
|---|---|---|
| \ (v/c\)” style="text-align:center; ">0.99 | \ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.1411 | \ (m/m_o\)” style="alinhamento do texto: centro; ">7.089 |
| \ (v/c\)” style="text-align:center; ">0,999 | \ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.0447 | \ (m/m_o\)” style="alinhamento do texto: centro; ">22,37 |
| \ (v/c\)” style="text-align:center; ">0.9999 | \ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.0141 | \ (m/m_o\)” style="alinhamento do texto: centro; ">70.7 |
Assim, de acordo com a Tabela\(\PageIndex{8}\):, se um objeto com massa de 100 kg estiver viajando a 0,9999c, sua massa se torna 7071 kg. Como nenhum objeto pode ter uma massa infinita, concluímos que nenhum objeto pode viajar à velocidade da luz ou a mais do que ela.
Conceitos-chave
- Uma tabela de valores ou gráfico pode ser usada para estimar um limite.
- Se o limite de uma função em um ponto não existir, ainda é possível que os limites da esquerda e da direita nesse ponto possam existir.
- Se os limites de uma função da esquerda e da direita existirem e forem iguais, o limite da função será esse valor comum.
- Podemos usar limites para descrever o comportamento infinito de uma função em um ponto.
Equações-chave
- Definição intuitiva do limite
\(\displaystyle \lim_{x \to a}f(x)=L\)
- Dois limites importantes
\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)
- Limites unilaterais
\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)
- Limites infinitos da esquerda
\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)
- Limites infinitos da direita
\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)
- Limites infinitos bilaterais
\(\displaystyle \lim_{x \to a}f(x)=+∞\):\(\displaystyle \lim_{x \to a^−}f(x)=+∞\) e\(\displaystyle \lim_{x \to a^+} f(x)=+∞\)
\(\displaystyle \lim_{x \to a}f(x)=−∞\):\(\displaystyle \lim_{x \to a^−}f(x)=−∞\) e\(\displaystyle \lim_{x \to a^+} f(x)=−∞\)
Glossário
- limite infinito
- Uma função tem um limite infinito em um ponto\(a\) se ela aumentar ou diminuir sem limite à medida que se aproxima.\(a\)
- definição intuitiva do limite
- Se todos os valores da função se\(f(x)\) aproximarem do número real\(L\) como os valores da\(x(≠a)\) abordagem a,\(f(x)\) se aproxima de L
- limite unilateral
- Um limite unilateral de uma função é um limite retirado da esquerda ou da direita
- assíntota vertical
- Uma função tem uma assíntota vertical em\(x=a\) se o limite à medida que se\(x\) aproxima\(a\) da direita ou da esquerda for infinito



Siga os procedimentos do Example\(\PageIndex{5}\).
uma\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\);.
b.\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\);
c.\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)
É útil ressaltar que as funções da forma\(f(x)=1/(x−a)^n\), onde n é um número inteiro positivo, têm limites infinitos à medida que\(x\) se aproximam\(a\) da esquerda ou da direita (Figura\(\PageIndex{9}\)). Esses limites estão resumidos nas definições acima.