2.7: Exemplos de álgebra de vetores

Exemplo\(\PageIndex{1}\): Analytical Computation of a Resultant

Três vetores de deslocamento\(\vec{A}\)\(\vec{B}\), e\(\vec{C}\) em um plano (Figura 2.3.6) são especificados por suas magnitudes A = 10,0, B = 7,0 e C = 8,0, respectivamente, e por seus respectivos ângulos de direção com a direção horizontal\(\alpha\) = 35°,\(\beta\) = −110°, e \(\gamma\)= 30°. As unidades físicas das magnitudes são centímetros. Resolva os vetores para seus componentes escalares e encontre as seguintes somas vetoriais:

1. \(\vec{R}\)=\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\),
2. \(\vec{D}\)=\(\vec{A}\) −\(\vec{B}\), e
3. \(\vec{S}\)=\(\vec{A}\) − 3\(\vec{B}\) +\(\vec{C}\).

Estratégia

Primeiro, usamos a Equação 2.4.13 para encontrar os componentes escalares de cada vetor e, em seguida, expressamos cada vetor em sua forma de componente vetorial dada por\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}\). Em seguida, usamos métodos analíticos de álgebra vetorial para encontrar os resultados.

Solução

Resolvemos os vetores fornecidos para seus componentes escalares:

\[ \begin{cases} A_{x} = A \cos \alpha = (10.0\; cm) \cos {35^{o}} = 8.19\; cm \\ A_{y} = A \sin \alpha = (10.0\; cm) \sin{35^{o}} = 5.73\; cm \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \beta = (7.0\; cm) \cos (-110^{o}) = -2.39\; cm \\ B_{y} = B \sin \beta= (7.0\; cm) \sin (-110^{o}) = -6.58\; cm \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \gamma= (8.0\; cm) \cos (30^{o}) = 6.93\; cm \\ C_{y} = C \sin \gamma= (8.0\; cm) \sin(30^{o}) = 4.00\; cm \end{cases}\]

Para (a) podemos substituir diretamente na Equação 2.6.7 para encontrar os componentes escalares da resultante:

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = 8.19\; cm - 2.39\; cm + 6.93\; cm = 12.73\; cm \\ R_{y} = A_{y} + B_{y} + C_{y} = 5.73\; cm - 6.58\; cm + 4.00\; cm = 3.15\; cm \end{cases}\]

Portanto, o vetor resultante é\(\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} = (12.7 \hat{i} + 3.1 \hat{j})\) cm. Para (b), podemos querer escrever a diferença vetorial como

\[\vec{D} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j}) - (B_{x} \hat{i} + B_{y} \hat{j}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} \ldotp\]

Portanto, o vetor de diferença é\(\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (10.6 \hat{i} + 12.3 \hat{j})\) cm.

Para (c), podemos escrever vetor\(\vec{S}\) na seguinte forma explícita:

\[ \vec{S} = \vec{A} - 3 \vec{B} + \vec{C} = (A_{x} \hat{i} + A_{y} \hat{j}) - 3(B_{x} \hat{i} + B_{y} \hat{j}) + (C_{x} \hat{i} + C_{y} \hat{j}) = (A_{x} - 3 B_{x} + C_{x}) \hat{i} + (A_{y} - 3 B_{y} + C_{y}) \hat{j} \ldotp\]

Então, os componentes escalares de\(\vec{S}\) são

\[ \begin{cases} S_{x} = A_{x} - 3B_{x} + C_{x} = 8.19\; cm - 3(-2.39\; cm) + 6.93\; cm = 22.29\; cm \\ S_{y} = A_{y} - 3B_{y} + C_{y} = 5.73\; cm -3(-6.58\; cm) + 4.00\; cm = 29.47\; cm \end{cases}\]

O vetor é\(\vec{S} = S_{x} \hat{i} + S_{y} \hat{j} = (22.3 \hat{i} + 29.5 \hat{j})\) cm.

Significância

Tendo encontrado os componentes vetoriais, podemos ilustrar os vetores representando graficamente ou podemos calcular magnitudes e ângulos de direção, conforme mostrado na Figura\(\PageIndex{1}\). Os resultados das magnitudes em (b) e (c) podem ser comparados com os resultados dos mesmos problemas obtidos com o método gráfico, mostrados na Figura 2.3.7 e na Figura 2.3.8. Observe que o método analítico produz resultados exatos e sua precisão não é limitada pela resolução de uma régua ou transferidor, como aconteceu com o método gráfico usado no Exemplo 2.3.2 para encontrar esse mesmo resultado.

Figura\(\PageIndex{1}\): Ilustração gráfica das soluções obtidas analiticamente.

Exercício 2.8

Três vetores de deslocamento\(\vec{A}\)\(\vec{B}\),, e\(\vec{F}\) (Figura 2.3.6) são especificados por suas magnitudes A = 10,00, B = 7,00 e F = 20,00, respectivamente, e por seus respectivos ângulos de direção com a direção horizontal\(\alpha\) = 35°,\(\beta\) = −110° e\(\varphi\) = 110 °. As unidades físicas das magnitudes são centímetros. Use o método analítico para encontrar o vetor\(\vec{F}\) =\(\vec{A}\) + 2\(\vec{B}\) −\(\vec{F}\). Verifique se G = 28,15 cm e se\(\theta_{G}\) = −68,65°.

Exemplo\(\PageIndex{2}\): The Tug-of-War Game

Quatro cães chamados Astro, Balto, Clifford e Dug jogam um jogo de cabo de guerra com um brinquedo (Figura\(\PageIndex{2}\)). Astro puxa o brinquedo na direção\(\alpha\) = 55° ao sul do leste, Balto puxa na direção\(\beta\) = 60° leste do norte e Clifford puxa na direção\(\gamma\) = 55° oeste do norte. Astro puxa fortemente com 160,0 unidades de força (N), que abreviamos como A = 160,0 N. Balto puxa ainda mais forte que Astro com uma força de magnitude B = 200,0 N, e Clifford puxa com uma força de magnitude C = 140,0 N. Quando Dug puxa o brinquedo de tal forma que sua força equilibra a resultante do outras três forças, o brinquedo não se move em nenhuma direção. Com quão grande é a força e em que direção Dug deve puxar o brinquedo para que isso aconteça?

Figura\(\PageIndex{2}\): Quatro cães jogam um jogo de cabo de guerra com um brinquedo.

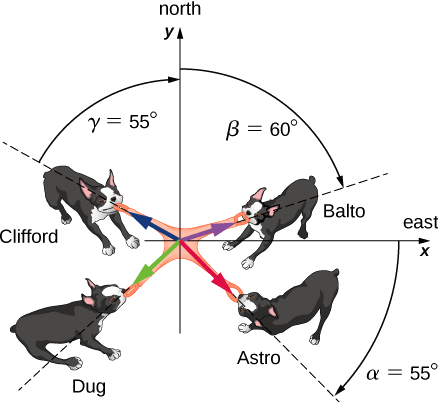
Estratégia

Assumimos que leste é a direção do eixo x positivo e norte é a direção do eixo y positivo. Como no exemplo\(\PageIndex{1}\), temos que resolver as três forças dadas -\(\vec{A}\) (a atração de Astro),\(\vec{B}\) (a atração de Balto) e\(\vec{C}\) (a atração de Clifford) - em seus componentes escalares e, em seguida, encontrar os componentes escalares do vetor resultante\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) + \(\vec{C}\). Quando a força\(\vec{D}\) de tração de Dug equilibra essa resultante, a soma de\(\vec{D}\) e\(\vec{R}\) deve fornecer o vetor nulo\(\vec{D}\) +\(\vec{R}\) =\(\vec{0}\). Isso significa que\(\vec{D}\) =\(- \vec{R}\) então a atração de Dug deve ser antiparalela\(\vec{R}\) a.

Solução

Os ângulos de direção são\(\theta_{A}\)\(− \alpha\) = −55°,\(\theta_{B}\) = 90° −\(\beta\) = 30° e\(\theta_{C}\) = 90° +\(\gamma\) = 145°, e substituindo-os na Equação 2.4.13 fornece os componentes escalares das três forças dadas:

\[ \begin{cases} A_{x} = A \cos \theta_{A} = (160.0\; N) \cos (-55^{o}) = + 91.8\; N \\ A_{y} = A \sin \theta_{A} = (160.0\; N) \sin (-55^{o}) = -131.1\; N \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \theta_{B} = (200.0\; N) \cos 30^{o} = + 173.2\; N \\ B_{y} = B \sin \theta_{B} = (200.0\; N) \sin 30^{o} = + 100.0\; N \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \theta_{C} = (140.0\; N) \cos 145^{o} = -114.7\; N \\ C_{y} = C \sin \theta_{C} = (140.0\; N) \sin 145^{o} = + 80.3\; N \end{cases}\]

Agora calculamos os componentes escalares do vetor resultante\(\vec{R} = \vec{A} + \vec{B} + \vec{C}\):

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = + 91.8\; N+ 173.2\; N- 114.7\; N = +150.3 \; N\\ R_{y} = A_{y} + B_{y} + C_{y} = -131.1\; N + 100.0\; N + 80.3\; N= +49.2\; N\end{cases}\]

O vetor antiparalelo ao resultante\(\vec{R}\) é

\[\vec{D} = -\vec{R} = -R_{x} \hat{i} - R_{y} \hat{j} = (-150.3 \hat{i} - 49.2 \hat{j}) N \ldotp\]

A magnitude da força de tração de Dug é

\[D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{(-150.3)^{2} + (-49.2)^{2}} N = 158.1\; N \ldotp\]

A direção da força de tração de Dug é

\[\theta = \tan^{-1} \left(\dfrac{D_{y}}{D_{x}}\right) = \tan^{-1} \left(\dfrac{-49.2\; N}{-150.3\; N}\right) = \tan^{-1} \left(\dfrac{49.2}{150.3}\right) = 18.1^{o}\ldotp\]

Dug puxa na direção 18,1° ao sul de oeste porque ambos os componentes são negativos, o que significa que o vetor de tração está no terceiro quadrante (Figura 2.4.4).

Exercício 2.9

Suponha que Balto in\(\PageIndex{2}\) Example saia do jogo para tratar de assuntos mais importantes, mas Astro, Clifford e Dug continuem jogando. A atração de Astro e Clifford pelo brinquedo não muda, mas Dug corre e morde o brinquedo em um lugar diferente. Com quão grande é a força e em que direção Dug deve puxar o brinquedo agora para equilibrar os puxões combinados de Clifford e Astro? Ilustre essa situação desenhando um diagrama vetorial indicando todas as forças envolvidas.

Exemplo\(\PageIndex{3}\): Vector Algebra

Determine a magnitude do vetor\(\vec{C}\) que satisfaz a equação 2\(\vec{A}\) − 6\(\vec{B}\) + 3\(\vec{C}\) = 2\(\hat{j}\),\(\vec{A}\) =\(\hat{i}\) − 2\(\hat{k}\) e\(\vec{B}\) = −\(\hat{j}\) +\(\frac{\hat{k}}{2}\).

Estratégia

Primeiro resolvemos a equação dada para o vetor desconhecido\(\vec{C}\). Em seguida, substituímos\(\vec{A}\) e\(\vec{B}\); agrupamos os termos ao longo de cada uma das três direções\(\hat{i}\)\(\hat{j}\),, e\(\hat{k}\); e identificamos os componentes escalares C _x, C _y e C _z. Finalmente, substituímos na Equação 2.5.6 para encontrar a magnitude C.

Solução

\[\begin{split} 2 \vec{A} - 6 \vec{B} +& 3 \vec{C} = 2 \hat{j}\\ & 3 \vec{C} = 2 \hat{j} - 2 \vec{A} + 6 \vec{B} \\ &\vec{C} = \frac{2}{3} \hat{j} - \frac{2}{3} \vec{A} + 2 \vec{B}\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} (\hat{i} - 2\hat{k}) + 2 \big(- \hat{j} + \frac{\hat{k}}{2}\big)\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} \hat{i} + \frac{4}{3} \hat{k} - 2 \hat{j} + \hat{k}\\ & \quad = -\frac{2}{3} \hat{i} + \big(\frac{2}{3} - 2 \big)\hat{j} + \big(\frac{4}{3}\ + 1 \big)\hat{k}\\ & \quad = -\frac{2}{3} \hat{i} - \frac{4}{3} \hat{j} + \frac{7}{3} \hat{k} \end{split}\]

Os componentes são C _x =\(-\frac{2}{3}\), C _y =\(-\frac{4}{3}\) e C _z =\(\frac{7}{3}\), e substituindo na Equação 2.5.6 dá

\[C = \sqrt{C_{x}^{2} + C_{y}^{2} + C_{z}^{2}} = \sqrt{\left(-\dfrac{2}{3}\right)^{2} + \left(-\dfrac{4}{3}\right)^{2} + \left(\dfrac{7}{3}\right)^{2}} = \sqrt{\frac{23}{3}} \ldotp\]

Exemplo\(\PageIndex{4}\): Displacement of a Skier

Começando em um chalé de esqui, um esquiador de cross-country vai 5,0 km ao norte, depois 3,0 km a oeste e, finalmente, 4,0 km ao sudoeste antes de descansar. Encontre seu vetor de deslocamento total em relação ao alojamento quando ele estiver no ponto de descanso. A que distância e em que direção ele deve esquiar do ponto de descanso para retornar diretamente ao chalé?

Estratégia

Assumimos um sistema de coordenadas retangulares com a origem no alojamento de esqui e com o vetor unitário\(\hat{i}\) apontando para o leste e o vetor unitário\(\hat{j}\) apontando para o norte. Há três deslocamentos:\(\vec{D}_{1}\),\(\vec{D}_{2}\),\(\vec{D}_{3}\) e. Identificamos suas magnitudes como D ₁ = 5,0 km, D ₂ = 3,0 km e D ₃ = 4,0 km. Identificamos que suas direções são os ângulos\(\theta_{1}\)\(\theta_{2}\) = 90°, = 180° e\(\theta_{3}\) = 180° + 45° = 225°. Resolvemos cada vetor de deslocamento em seus componentes escalares e substituímos os componentes na Equação 2.6.5 para obter os componentes escalares do deslocamento resultante\(\vec{D}\) do alojamento até o ponto de descanso. No caminho de volta do ponto de descanso para o alojamento, o deslocamento é\(\vec{B}\) = −\(\vec{D}\). Finalmente, encontramos a magnitude e a direção de\(\vec{B}\).

Solução

Os componentes escalares dos vetores de deslocamento são

\[ \begin{cases} D_{1x} = D_{1} \cos \theta_{1} = (5.0\; km) \cos 90^{o} = 0 \\ D_{1y} = D_{1} \sin \theta_{1} = (5.0\; km) \sin 90^{o} = 5.0\; km \end{cases}\]

\[ \begin{cases} D_{2x} = D_{2} \cos \theta_{2} = (3.0\; km) \cos 180^{o} = -3.0 \;km\\ D_{2y} = D_{2} \sin \theta_{2} = (3.0\; km) \sin 180^{o} = 0 \end{cases}\]

\[ \begin{cases} D_{3x} = D_{3} \cos \theta_{3} = (4.0\; km) \cos 225^{o} = -2.8\; km \\ D_{3y} = D_{3} \sin \theta_{3} = (4.0\; km) \sin 225^{o} = -2.8\; km \end{cases}\]

Os componentes escalares do vetor de deslocamento líquido são

\[ \begin{cases} D_{x} = D_{1x} + D_{2x} + D_{3x} = (0 - 3.0 - 2.8)km = -5.8\; km \\ D_{y} = D_{1y} + D_{2y} + D_{3y} = (5.0 + 0 - 2.8)km = + 2.2\; km \end{cases}\]

Portanto, o vetor de deslocamento da rede do esquiador é\(\vec{D}\) = D _x\(\hat{i}\) + D _y\(\hat{j}\) = (−5,8\(\hat{i}\) + 2,2\(\hat{j}\)) km. No caminho de volta ao alojamento, seu deslocamento é\(\vec{B}\) = −\(\vec{D}\) = − (−5,8\(\hat{i}\) + 2,2\(\hat{j}\)) km = (5,8\(\hat{i}\) − 2,2\(\hat{j}\)) km. Sua magnitude é B =\(\sqrt{B_{x}^{2} + B_{y}^{2}}\) =\(\sqrt{(5.8)^{2} + (−2.2)^{2}}\) km = 6,2 km e seu ângulo de direção é\(\theta\) = tan ⁻¹\(\left(\dfrac{−2.2}{5.8}\right)\) = −20,8°. Portanto, para retornar à pousada, ele deve percorrer 6,2 km em uma direção cerca de 21° ao sul do leste.

Significância

Observe que nenhum valor é necessário para resolver esse problema pelo método analítico. Os números são necessários ao usar um método gráfico; no entanto, podemos verificar se nossa solução faz sentido esboçando-a, o que é uma etapa final útil na solução de qualquer problema vetorial.

Exemplo\(\PageIndex{5}\): Displacement of a Jogger

Um corredor sobe um lance de 200 degraus idênticos até o topo de uma colina e depois corre ao longo do topo da colina 50,0 m antes de parar em um bebedouro (Figura\(\PageIndex{3}\)). Seu vetor de deslocamento do ponto A na parte inferior dos degraus até o ponto B na fonte é\(\vec{D}_{AB}\) = (−90,0\(\hat{i}\) + 30,0\(\hat{j}\)) m. Qual é a altura e a largura de cada degrau no voo? Qual é a distância real que o corredor percorre? Se ele fizer um loop e retornar ao ponto A, qual é seu vetor de deslocamento líquido?

Figura\(\PageIndex{3}\): Um corredor sobe um lance de degraus.

Estratégia

O vetor de deslocamento\(\vec{D}_{AB}\) é a soma vetorial do vetor de deslocamento do corredor\(\vec{D}_{AT}\) ao longo da escada (do ponto A na parte inferior da escada ao ponto T no topo da escada) e seu vetor de deslocamento\(\vec{D}_{RB}\) no topo da colina (do ponto T no topo da escada até o fonte no ponto B). Devemos encontrar os componentes horizontal e vertical do\(\vec{D}_{TB}\). Se cada degrau tiver largura w e altura h, o componente horizontal de\(\vec{D}_{TB}\) deve ter um comprimento de 200w e o componente vertical deve ter um comprimento de 200h. A distância real que o corredor percorre é a soma da distância que ele sobe as escadas e a distância de 50,0 m que ele percorre ao longo do topo da colina.

Solução

No sistema de coordenadas indicado na Figura\(\PageIndex{3}\), o vetor de deslocamento do corredor no topo da colina é\(\vec{D}_{RB}\) = (−50,0 m)\(\hat{i}\). Seu vetor de deslocamento líquido é

\[\vec{D}_{AB} = \vec{D}_{AT} + \vec{D}_{TB} \ldotp \nonumber\]

Portanto, seu vetor de deslocamento\(\vec{D}_{TB}\) ao longo das escadas é

\[\begin{split} \vec{D}_{AT}& = \vec{D}_{AB} - \vec{D}_{TB} = (-90.0 \hat{i} + 30.0 \hat{j})m - (-50.0 m)\hat{i}) = [(-90.0 50.0) hat{i} + 30.0 \hat{j})]m \\ & = (-40.0 \hat{i} + 30.0 \hat{j})m \ldotp \end{split}\]

Seus componentes escalares são D _AtX = −40,0 m e D _ATy = 30,0 m. Portanto, devemos ter

\[200 w=|-40.0| \mathrm{m} \text { and } 200 h=30.0 \: \mathrm{m} \ldotp \nonumber\]

Portanto, a largura do degrau é w\(\frac{40.0\; m}{200}\) = 0,2 m = 20 cm e a altura do degrau é w\(\frac{30.0\; m}{200}\) = = 0,15 m = 15 cm. A distância que o corredor percorre ao longo da escada é

\[\vec{D}_{AT} = \sqrt{\vec{D}_{ATx}^{2} + \vec{D}_{ATy}^{2}} = \sqrt{(-40.0)^{2} + (30.0)^{2}}m = 50.0\; m \ldotp \nonumber\]

Assim, a distância real que ele percorre é D _AT + D _TB = 50,0 m + 50,0 m = 100,0 m. Quando ele faz um loop e volta da fonte para sua posição inicial no ponto A, a distância total que ele percorre é o dobro dessa distância, ou 200,0 m. No entanto, seu vetor de deslocamento líquido é zero, porque quando sua posição final é a mesma de sua posição inicial, os componentes escalares de seu vetor de deslocamento líquido são zero (Equação 2.4.4).

Em muitas situações físicas, muitas vezes precisamos saber a direção de um vetor. Por exemplo, podemos querer saber a direção de um vetor de campo magnético em algum ponto ou a direção do movimento de um objeto. Já dissemos que a direção é dada por um vetor unitário, que é uma entidade adimensional, ou seja, não tem unidades físicas associadas a ela. Quando o vetor em questão está ao longo de um dos eixos em um sistema cartesiano de coordenadas, a resposta é simples, porque então seu vetor unitário de direção é paralelo ou antiparalelo à direção do vetor unitário de um eixo. Por exemplo, a direção do vetor\(\vec{d}\) = -5 m\(\hat{i}\) é vetor unitário\(\vec{d}\) = -\(\hat{i}\). A regra geral para encontrar o vetor unitário\(\vec{V}\) de direção para qualquer vetor\(\vec{V}\) é dividi-lo por sua magnitude V:

\[\widehat{\mathbf{V}}=\frac{\overrightarrow{\mathbf{V}}}{V} \label{2.26} \cdot \]

Vemos nessa expressão que o vetor unitário de direção é de fato adimensional porque o numerador e o denominador na Equação\ ref {2.26} têm a mesma unidade física. Dessa forma, a Equação\ ref {2.26} nos permite expressar o vetor unitário de direção em termos de vetores unitários dos eixos. O exemplo a seguir ilustra esse princípio.

Exemplo\(\PageIndex{6}\): The Unit Vector of Direction

Se o vetor de velocidade do comboio militar no Exemplo 2.6.1 for\(\vec{v}\) = (4.000\(\hat{i}\) + 3.000\(\hat{j}\) + 0,100\(\hat{k}\)) km/h, qual é o vetor unitário de sua direção de movimento.

Estratégia

O vetor unitário da direção do movimento do comboio é o vetor unitário\(\hat{v}\) que é paralelo ao vetor de velocidade. O vetor unitário é obtido dividindo um vetor por sua magnitude, de acordo com a Equação\ ref {2.26}.

Solução

A magnitude do vetor\(\vec{v}\) é

\[v = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} = \sqrt{4.000^{2} + 3.000^{2} + 0.100^{2}}km/h = 5.001\; km/h \ldotp \nonumber\]

Para obter o vetor unitário\(\hat{v}\), divida\(\vec{v}\) por sua magnitude:

\[\begin{split} \hat{v}& = \frac{\vec{v}}{v} = \frac{(4.000 \hat{i} + 3.00 \hat{j} + 0.100 \hat{k})km/h}{5.001\; km/h} \\ & = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.1100 \hat{k})}{5.001} \\ & = \frac{4.000}{5.001} \hat{i} + \frac{3.000}{5.001} \hat{j} + \frac{0.100}{5.001} \hat{k} \\ & = (79.98 \hat{i} + 59.99 \hat{j} + 2.00 \hat{k}) \times 10^{-2} \ldotp \end{split}\]

Significância

Observe que, ao usar o método analítico com uma calculadora, é aconselhável realizar seus cálculos com pelo menos três casas decimais e, em seguida, arredondar a resposta final para o número necessário de números significativos, que é a forma como realizamos os cálculos neste exemplo. Se você finalizar sua resposta parcial muito cedo, corre o risco de sua resposta final ter um grande erro numérico, e ela pode estar longe da resposta exata ou de um valor medido em um experimento.

Exercício 2.10

Verifique se o vetor\(\hat{v}\) obtido no Exemplo\(\PageIndex{3}\) é de fato um vetor unitário calculando sua magnitude. Se o comboio no Exemplo 2.6.1 estava se movendo em uma planície desértica, ou seja, se o terceiro componente de sua velocidade fosse zero, qual é o vetor unitário de sua direção de movimento? Qual direção geográfica ela representa?