Skip to main content
Global

11.3E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183702

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Exercício\(\PageIndex{17}\) Graph Vertical Parabolas

    Nos exercícios a seguir, represente graficamente cada equação usando propriedades.

    1. \(y=-x^{2}+4 x-3\)
    2. \(y=-x^{2}+8 x-15\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(y=8 x^{2}-10 x+3\)
    Resposta

    1.

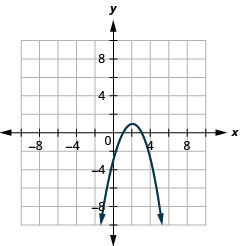
    Este gráfico mostra uma parábola se abrindo para baixo com vértice (2, 1) e interceptos x (1, 0) e (3, 0).
    Figura 11.2.83

    3.

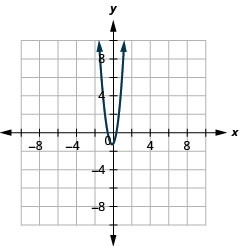
    Este gráfico mostra uma parábola se abrindo para cima. O vértice é (menos 0,167, menos 1,167), os interceptos x são (menos 0,608) e (menos 0,274, 0) e o intercepto y é (0, menos 1).
    Figura 11.2.84
    Exercício\(\PageIndex{18}\) Graph Vertical Parabolas

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e
    2. Use as propriedades da forma padrão para representar graficamente a equação.
    1. \(y=-x^{2}+2 x-4\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(y=-2 x^{2}-4 x-5\)
    4. \(y=3 x^{2}-12 x+7\)
    Resposta

    1.

    1. \(y=-(x-1)^{2}-3\)
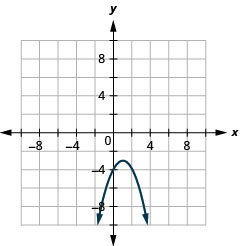
    Este gráfico mostra uma parábola se abrindo para baixo com vértice (1, menos 3) e intercepto y (0, 4).
    Figura 11.2.85

    3.

    1. \(y=-2(x+1)^{2}-3\)
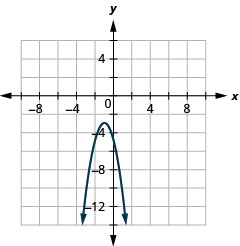
    Este gráfico mostra uma parábola se abrindo para baixo com vértice (menos 1, menos 3) e interceptos x (menos 5, 0).
    Figura 11.2.86
    Exercício\(\PageIndex{19}\) Graph Horizontal Parabolas

    Nos exercícios a seguir, represente graficamente cada equação usando propriedades.

    1. \(x=-2 y^{2}\)
    2. \(x=3 y^{2}\)
    3. \(x=4 y^{2}\)
    4. \(x=-4 y^{2}\)
    5. \(x=-y^{2}-2 y+3\)
    6. \(x=-y^{2}-4 y+5\)
    7. \(x=y^{2}+6 y+8\)
    8. \(x=y^{2}-4 y-12\)
    9. \(x=(y-2)^{2}+3\)
    10. \(x=(y-1)^{2}+4\)
    11. \(x=-(y-1)^{2}+2\)
    12. \(x=-(y-4)^{2}+3\)
    13. \(x=(y+2)^{2}+1\)
    14. \(x=(y+1)^{2}+2\)
    15. \(x=-(y+3)^{2}+2\)
    16. \(x=-(y+4)^{2}+3\)
    17. \(x=-3(y-2)^{2}+3\)
    18. \(x=-2(y-1)^{2}+2\)
    19. \(x=4(y+1)^{2}-4\)
    20. \(x=2(y+4)^{2}-2\)
    Resposta

    1.

    Este gráfico mostra uma parábola se abrindo para a esquerda com vértice (0, 0). Dois pontos nele são (menos 2, 1) e (menos 2, menos 1).
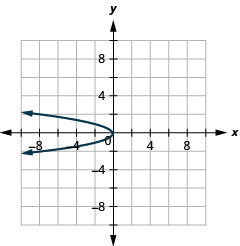
    Figura 11.2.87

    3.

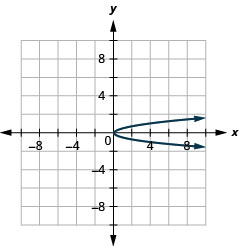
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (0, 0). Dois pontos são (4, 1) e (4, menos 1).
    Figura 11.2.88

    5.

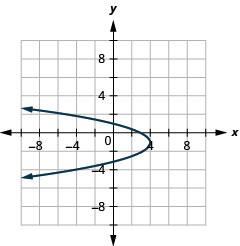
    Este gráfico mostra uma parábola se abrindo para a esquerda com vértice (4, menos 1) e interceptos y (0, 1) e (0, menos 3).
    Figura 11.2.89

    7.

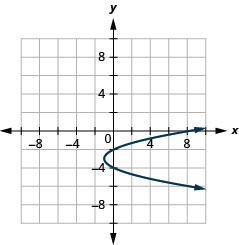
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (menos 1, menos 3) e interceptos y (0, menos 2) e (0, menos 4).
    Figura 11.2.90

    9.

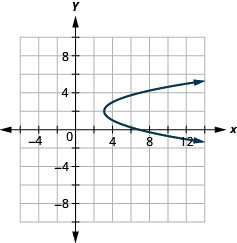
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (3, 2) e intercepto x (7, 0).
    Figura 11.2.91

    11.

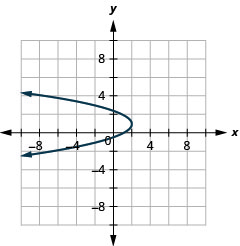
    Este gráfico mostra uma parábola se abrindo para a esquerda com vértice (2, 1) e intercepto x (1, 0).
    Figura 11.2.92

    13.

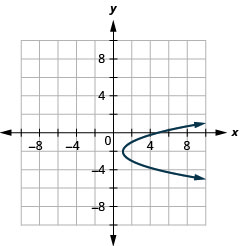
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (1, menos 2) e intercepto x (5, 0).
    Figura 11.2.93

    15.

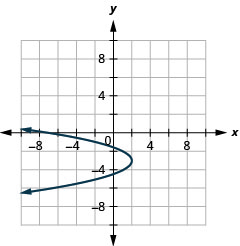
    Este gráfico mostra uma parábola se abrindo para a esquerda com vértice (2, menos 3). Dois pontos nele são (menos 2, menos 1) e (menos 2, 5).
    Figura 11.2.94

    17.

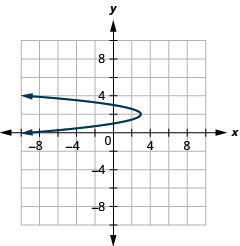
    Este gráfico mostra uma parábola que se abre à esquerda com vértice (3, 2) e interceptos y (0, 1) e (0, 3).
    Figura 11.2.95

    19.

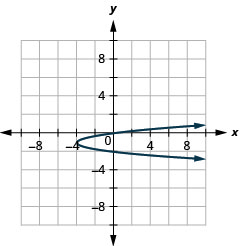
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (menos 4, menos 1) e interceptos y (0, 0) e (0, menos 2).
    Figura 11.2.96
    Exercício\(\PageIndex{20}\) Graph Horizontal Parabolas

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e
    2. Use as propriedades da forma padrão para representar graficamente a equação.
    1. \(x=y^{2}+4 y-5\)
    2. \(x=y^{2}+2 y-3\)
    3. \(x=-2 y^{2}-12 y-16\)
    4. \(x=-3 y^{2}-6 y-5\)
    Resposta

    1.

    1. \(x=(y+2)^{2}-9\)
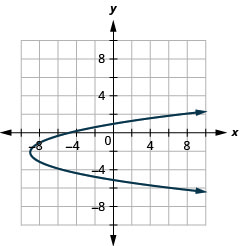
    Este gráfico mostra uma parábola se abrindo para a direita com vértice (menos 9, menos 2) e interceptos y (0, 1) e (0, menos 5).
    Figura 11.2.97

    3.

    1. \(x=-2(y+3)^{2}+2\)
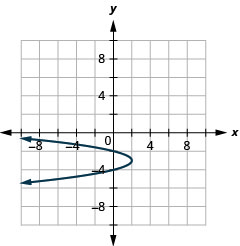
    Este gráfico mostra uma parábola se abrindo para a esquerda com vértice (2, menos 3) e interceptos y (0, menos 2) e (0, menos 4).
    Figura 11.2.98
    Exercício\(\PageIndex{21}\) Mixed Practice

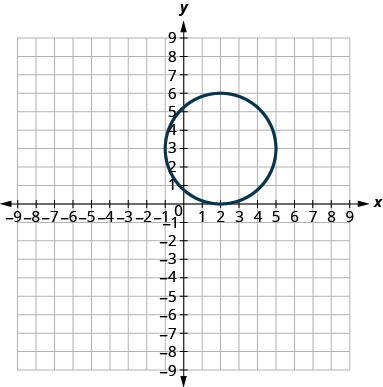
    Nos exercícios a seguir, combine cada gráfico com uma das seguintes equações:

    1. \(x^{2}+y^{2}=64\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \((x-2)^{2}+(y-3)^{2}=9\)
    5. \(y=-x^{2}+8 x-15\)
    6. \(y=6 x^{2}+2 x-1\)

    1.

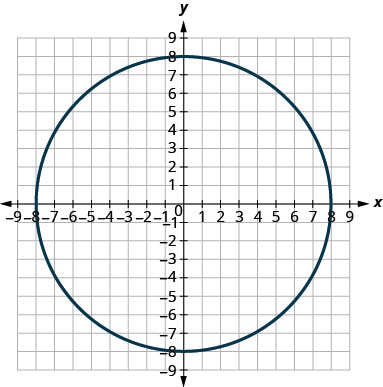
    Este gráfico mostra o círculo com o centro (0, 0) e o raio 8 unidades.
    Figura 11.2.99

    2.

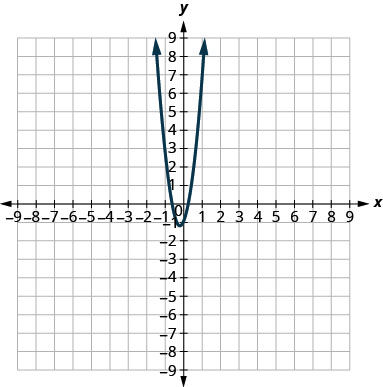
    Este gráfico mostra uma parábola se abrindo para cima. Seu vértice tem um valor x ligeiramente menor que 0 e um valor y ligeiramente menor que menos 1. Um ponto nele está próximo de (menos 1, 3).
    Figura 11.2.100

    3.

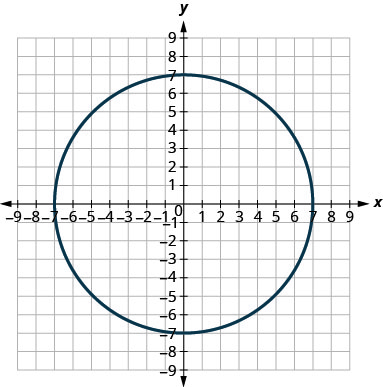
    Este gráfico mostra o círculo com unidades de centro (0, 0) e raio 7.
    Figura 11.2.101

    4.

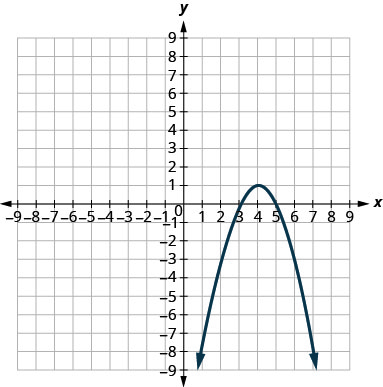
    Este gráfico mostra uma parábola se abrindo para baixo com vértice (4, 1) e interceptos x (3, 0) e (5, 0).
    Figura 11.2.102

    5.

    Este gráfico mostra o círculo com unidades de centro (2, 3) e raio 3.
    Figura 11.2.103

    6.

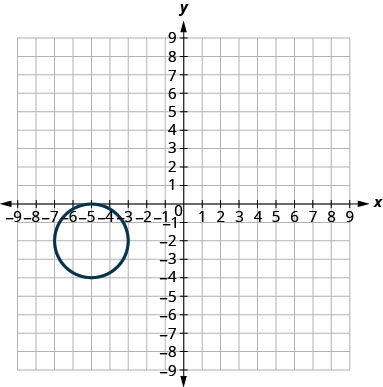
    Este gráfico mostra o círculo com unidades de centro (menos 5, menos 2) e raio 2.
    Figura 11.2.104
    Resposta

    1. uma

    3,2 kg

    5,2 d

    Exercício\(\PageIndex{22}\) Solve Applications with Parabolas

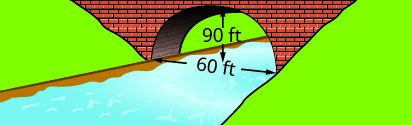
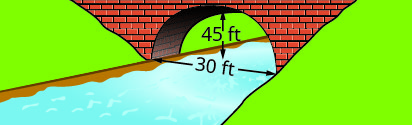
    Escreva a equação na forma padrão do arco parabólico formado na base da ponte mostrada. Use o lado inferior esquerdo da ponte como origem\((0, 0)\).

    1.

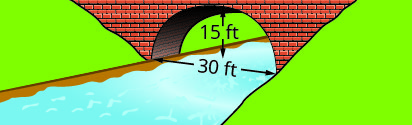
    Este gráfico mostra o círculo com unidades de centro (menos 5, menos 2) e raio 2.
    Figura 11.2.105

    2.

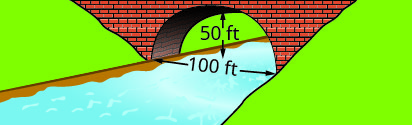
    Esta figura mostra um arco parabólico formado na base de uma ponte. Tem 50 pés de altura e 100 pés de largura na base.
    Figura 11.2.106

    3.

    Esta figura mostra um arco parabólico formado na base de uma ponte. Tem 90 pés de altura e 60 pés de largura na base.
    Figura 11.2.107

    4.

    Esta figura mostra um arco parabólico formado na base de uma ponte. Tem 45 pés de altura e 30 pés de largura na base.
    Figura 11.2.108
    Resposta

    1. \(y=-\frac{1}{15}(x-15)^{2}+15\)

    3. \(y=-\frac{1}{10}(x-30)^{2}+90\)

    Exercício\(\PageIndex{23}\) Writing Exercises
    1. Com suas próprias palavras, defina uma parábola.
    2. A parábola é\(y=x^{2}\) uma função? A parábola é\(x=y^{2}\) uma função? Explique por que ou por que não.
    3. Escreva a equação de uma parábola que se abre para cima ou para baixo na forma padrão e a equação de uma parábola que se abre para a esquerda ou para a direita na forma padrão. Forneça um esboço da parábola para cada uma, rotule o vértice e o eixo de simetria.
    4. Explique com suas próprias palavras, como você pode saber, pela equação, se uma parábola se abre para cima, para baixo, para a esquerda ou para a direita.
    Resposta

    1. As respostas podem variar

    3. As respostas podem variar

    Verificação automática

    a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

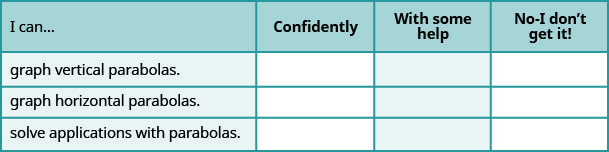
    Essa tabela tem quatro colunas, 3 linhas e uma linha de cabeçalho. A linha do cabeçalho rotula cada coluna que eu posso, com confiança, com alguma ajuda e não, eu não entendo.™ A primeira coluna tem as seguintes afirmações: representar graficamente parábolas verticais, representar graficamente parábolas horizontais, resolver aplicações com parábolas. As colunas restantes estão em branco.
    Figura 11.2.109

    b. Depois de analisar essa lista de verificação, o que você fará para se tornar confiante em todos os objetivos?