11.3: Parábolas

Objetivos de

Ao final desta seção, você poderá:

• Parábolas verticais gráficas
• Parábolas horizontais do gráfico
• Resolva aplicativos com parábolas

Esteja preparado

Antes de começar, faça este teste de prontidão.

1. Gráfico:$y=-3 x^{2}+12 x-12$.
   Se você perdeu esse problema, consulte o Exemplo 9.47.
2. Resolva completando o quadrado:$x^{2}-6 x+6=0$.
   Se você perdeu esse problema, consulte o Exemplo 9.12.
3. Escreva em formato padrão:$y=3 x^{2}-6 x+5$.
   Se você perdeu esse problema, consulte o Exemplo 9.59.

Parábolas verticais do gráfico

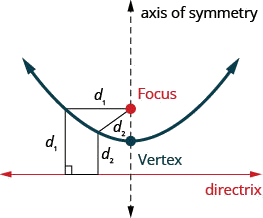
A próxima seção cônica que veremos é uma parábola. Definimos uma parábola como todos os pontos em um plano que estão à mesma distância de um ponto fixo e de uma linha fixa. O ponto fixo é chamado de foco e a linha fixa é chamada de diretriz da parábola.

Figura 11.2.1

Definição$\PageIndex{1}$: Parabola, Focus, and Directrix

Uma parábola são todos os pontos em um plano que estão à mesma distância de um ponto fixo e de uma linha fixa. O ponto fixo é chamado de foco e a linha fixa é chamada de diretriz da parábola.

Figura 11.2.2

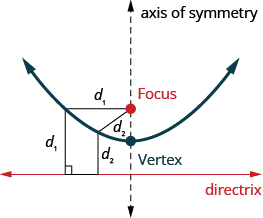
Anteriormente, aprendemos a representar graficamente parábolas verticais a partir da forma geral ou da forma padrão usando propriedades. Esses métodos também funcionarão aqui. Vamos resumir as propriedades aqui.

Parábolas verticais

Tabela 11.2.1

	Formulário geral $y=a x^{2}+b x+c$	Formulário padrão $y=a(x-h)^{2}+k$
Orientação	\ (y=a x^ {2} +b x+c\) "> para$a>0$ cima;$a<0$ para baixo	\ (y=a (x-h) ^ {2} +k\) "> para$a>0$ cima;$a<0$ para baixo
Eixo de simetria	\ (y=a x^ {2} +b x+c\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Vértice	\ (y=a x^ {2} +b x+c\) ">Substituir$x=-\dfrac{b}{2 a}$ e resolver por$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-interceptar	\ (y=a x^ {2} +b x+c\) ">Deixe$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Deixe$x=0$
$x$-intercepta	\ (y=a x^ {2} +b x+c\) ">Deixe$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Deixe$y=0$

Os gráficos mostram a aparência das parábolas quando se abrem para cima ou para baixo. Sua posição em relação ao$y$ eixo$x$ - ou -é meramente um exemplo.

Figura 11.2.3

Para representar graficamente uma parábola a partir desses formulários, usamos as etapas a seguir.

Representação gráfica de parábolas verticais

Como representar graficamente parábolas verticais$y=a x^{2}+b x+c$ ou$f(x)=a(x-h)^{2}+k$ usar propriedades.

• Etapa 1: Determine se a parábola se abre para cima ou para baixo.
• Etapa 2. Encontre o eixo de simetria.
• Etapa 3. Encontre o vértice.
• Etapa 4. Encontre o$y$ intercepto -. Encontre o ponto simétrico ao$y$ intercepto -no eixo de simetria.
• Etapa 5. Encontre as$x$ interceptações -.
• Etapa 6. Faça um gráfico da parábola.

O próximo exemplo analisa o método de representação gráfica de uma parábola a partir da forma geral de sua equação.

Exemplo$\PageIndex{1}$

Faça um gráfico$y=-x^{2}+6 x-8$ usando propriedades.

Solução:

Tabela 11.2.2

	$\begin{align*} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt]  \color{black}{y} &=-x^{2}+6 x-8 \end{align*}$
Desde então$a$$-1$, a parábola se abre para baixo.
Para encontrar o eixo de simetria, encontre$x=-\dfrac{b}{2 a}$.	$\begin{align*} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align*}$
	O eixo de simetria é$x=3$.
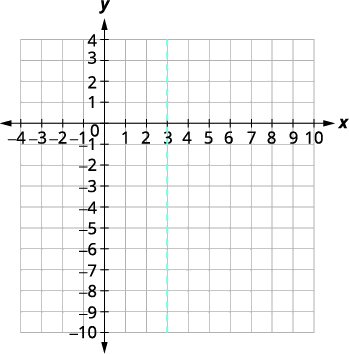O vértice está na linha$x=3$.	$y=-x^{2}+6 x-8$
Deixe$x=3$.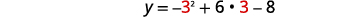
	$\begin{align*} y &=-9+18-8 \\[4pt] y &=1 \end{align*}$
	O vértice é$(3,1)$.
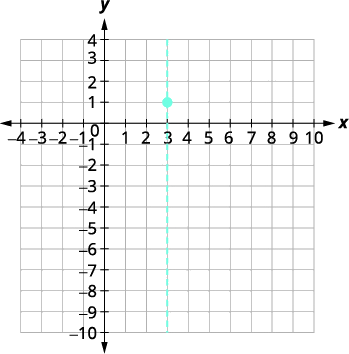O$y$ -intercept ocorre quando$x=0$.	$y=-x^{2}+6 x-8$
Substituto$x=0$.	$y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8$
Simplifique.	$y=-8$
	O$y$ intercepto -é$(0,-8)$.
O ponto$(0,−8)$ é três unidades à esquerda da linha de simetria. O ponto três unidades à direita da linha de simetria é$(6,−8)$.	O ponto simétrico ao$y$ intercepto -é$(6,−8)$.
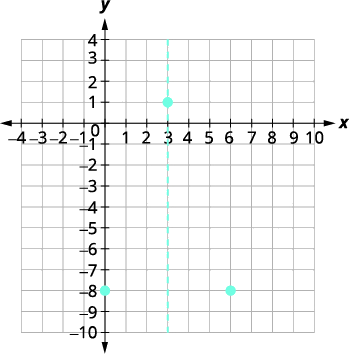O$x$ -intercept ocorre quando$y=0$.	$y=-x^{2}+6 x-8$
Deixe$y=0$.	$\color{red}{0} \color{black}{=}-x^{2}+6 x-8$
Considere o GCF.	$0=-\left(x^{2}-6 x+8\right)$
Considere o trinômio.	$0=-(x-4)(x-2)$
Resolva para$x$.	$x=4, \quad x=2$
	As$x$ interceptações -são$(4,0),(2,0)$.
Faça um gráfico da parábola.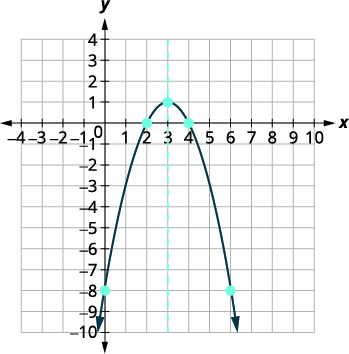

Exercício$\PageIndex{1}$

Faça um gráfico$y=-x^{2}+5 x-6$ usando propriedades.

Resposta

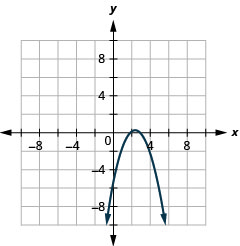
Figura 11.2.24

Exercício$\PageIndex{2}$

Faça um gráfico$y=-x^{2}+8 x-12$ usando propriedades.

Resposta

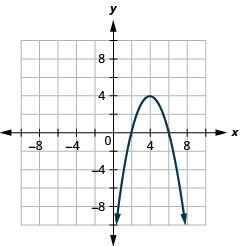
Figura 11.2.25

O próximo exemplo analisa o método de representação gráfica de uma parábola a partir da forma padrão de sua equação,$y=a(x-h)^{2}+k$.

Exemplo$\PageIndex{2}$

Escreva$y=3 x^{2}-6 x+5$ na forma padrão e, em seguida, use as propriedades da forma padrão para representar graficamente a equação.

Solução:

Tabela 11.2.3

Reescreva a função na$y=a(x-h)^{2}+k$ forma completando o quadrado.	$\begin{align*} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3  \\[4pt] y &=3(x-1)^{2}+2 \end{align*}$
Identifique as constantes$a, h, k$.	$a=3, h=1, k=2$
Desde então$a=2$, a parábola se abre para cima.
O eixo de simetria é$x=h$.	O eixo de simetria é$x=1$.
O vértice é$(h,k)$.	O vértice é$(1,2)$.
Encontre o$y$ intercepto -substituindo$x=0$,	$\begin{align*} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align*}$
	$y$-interceptar$(0,5)$
Encontre o ponto simétrico ao$(0,5)$ outro lado do eixo de simetria.	$(2,5)$
Encontre as$x$ interceptações -.	$\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}$
	A raiz quadrada de um número negativo nos diz que as soluções são números complexos. Portanto, não há$x$ interceptações.
Faça um gráfico da parábola.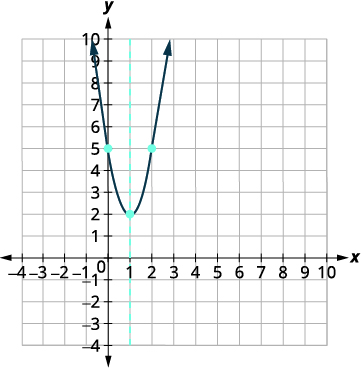

Exercício$\PageIndex{3}$

1. Escreva$y=2 x^{2}+4 x+5$ em formato padrão e
2. use propriedades da forma padrão para representar graficamente a equação.

Resposta

1. $y=2(x+1)^{2}+3$
2.  

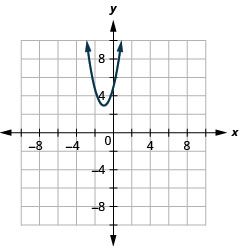
Figura 11.2.28

Exercício$\PageIndex{4}$

1. Escreva$y=-2 x^{2}+8 x-7$ em formato padrão e
2. use propriedades da forma padrão para representar graficamente a equação.

Resposta

1. $y=-2(x-2)^{2}+1$
2.  

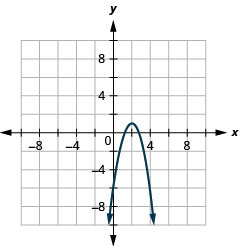
Figura 11.2.29

Parábolas horizontais do gráfico

Nosso trabalho até agora tratou apenas de parábolas que se abrem para cima ou para baixo. Agora vamos examinar as parábolas horizontais. Essas parábolas se abrem para a esquerda ou para a direita. Se trocarmos o$x$ e$y$ em nossas equações anteriores por parábolas, obteremos as equações para as parábolas que se abrem para a esquerda ou para a direita.

Parábolas horizontais

Tabela 11.2.4

	Formulário geral $x=a y^{2}+b y+c$	Formulário padrão $x=a(y-k)^{2}+h$
Orientação	\ (x=a y^ {2} +b y+c\) ">$a>0$ direita;$a<0$ esquerda	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ direita;$a<0$ esquerda
Eixo de simetria	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Vértice	\ (x=a y^ {2} +b y+c\) ">Substituir$y=-\dfrac{b}{2 a}$ e resolver por$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-intercepta	\ (x=a y^ {2} +b y+c\) ">Deixe$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Deixe$x=0$
$y$-interceptar	\ (x=a y^ {2} +b y+c\) ">Deixe$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Deixe$y=0$

Os gráficos mostram a aparência das parábolas quando estão à esquerda ou à direita. Sua posição em relação ao$y$ eixo$x$ - ou -é meramente um exemplo.

Figura 11.2.30

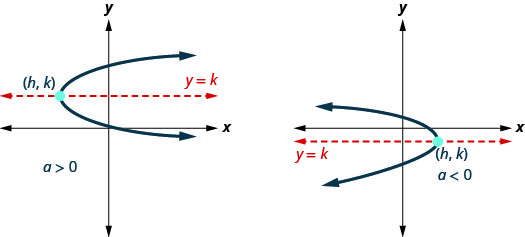
Olhando para essas parábolas, seus gráficos representam uma função? Como os dois gráficos falhariam no teste da linha vertical, eles não representam uma função.

Representar graficamente uma parábola que se abre para a esquerda ou para a direita é basicamente o mesmo que fizemos com as parábolas que se abrem para cima ou para baixo, com a reversão das$y$ variáveis$x$ e.

Como: Representar graficamente parábolas horizontais$y=a x^{2}+b x+c$ or $f(x)=a(x-h)^{2}+k$ using Properties

• Etapa 1: Determine se a parábola se abre para a esquerda ou para a direita.
• Etapa 2: Encontre o eixo de simetria.
• Etapa 3: Encontre o vértice.
• Etapa 4: Encontre o$x$ -intercept. Encontre o ponto simétrico ao$x$ intercepto -no eixo de simetria.
• Etapa 5: Encontre$y$ os interceptos.
• Etapa 6: Faça um gráfico da parábola.

Exemplo$\PageIndex{3}$

Faça um gráfico$x=2 y^{2}$ usando propriedades.

Solução:

Tabela 11.2.5

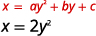Desde então$a=2$, a parábola se abre para a direita.
Para encontrar o eixo de simetria, encontre$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{0}{2(2)}$
	$y=0$
	O eixo de simetria é$y=0$.
O vértice está na linha$y=0$.	$x=2 y^{2}$
Deixe$y=0$.
	$x=0$
	O vértice é$(0,0)$.

Como o vértice é$(0,0)$, os$y$ interceptos$x$ - e -são o ponto$(0,0)$. Para representar graficamente a parábola, precisamos de mais pontos. Nesse caso, é mais fácil escolher valores de$y$.

Figura 11.2.38

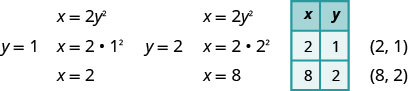
Também traçamos os pontos simétricos para$(2,1)$ e$(8,2)$ através do$y$ eixo -, os pontos$(2,−1),(8,−2)$.

Faça um gráfico da parábola.

Figura 11.2.39

Exercício$\PageIndex{5}$

Faça um gráfico$x=y^{2}$ usando propriedades.

Resposta

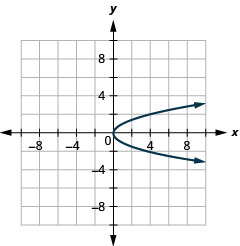
Figura 11.2.40

Exercício$\PageIndex{6}$

Faça um gráfico$x=-y^{2}$ usando propriedades.

Resposta

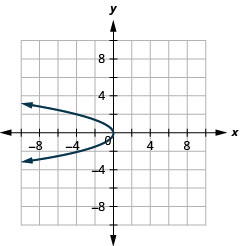
Figura 11.2.41

No próximo exemplo, o vértice não é a origem.

Exemplo$\PageIndex{4}$

Faça um gráfico$x=-y^{2}+2 y+8$ usando propriedades.

Solução:

Tabela 11.2.6

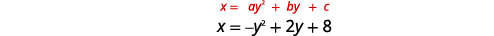Desde então$a=-1$, a parábola se abre para a esquerda.
Para encontrar o eixo de simetria, encontre$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{2}{2(-1)}$
	$y=1$
	O eixo de simetria é$y=1$.
O vértice está na linha$y=1$.	$x=-y^{2}+2 y+8$
Deixe$y=1$.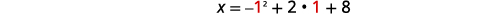
	$x=9$
	O vértice é$(9,1)$.
O$x$ -intercept ocorre quando$y=0$.	$x=-y^{2}+2 y+8$
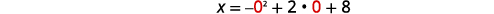	$x=8$
	O$x$ intercepto -é$(8,0)$.
O ponto$(8,0)$ está uma unidade abaixo da linha de simetria. O ponto simétrico uma unidade acima da linha de simetria é$(8,2)$	O ponto simétrico é$(8,2)$.
O$y$ -intercept ocorre quando$x=0$.	$x=-y^{2}+2 y+8$
Substituto$x=0$.	$0=-y^{2}+2 y+8$
Resolver.	$y^{2}-2 y-8=0$
	$(y-4)(y+2)=0$
	$y=4, \quad  y=-2$
	As$y$ interceptações -são$(0,4)$$(0,-2)$ e.
Conecte os pontos para representar graficamente a parábola.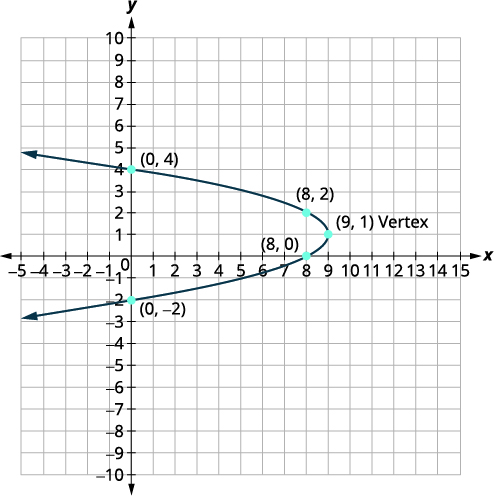

Exercício$\PageIndex{7}$

Faça um gráfico$x=-y^{2}-4 y+12$ usando propriedades.

Resposta

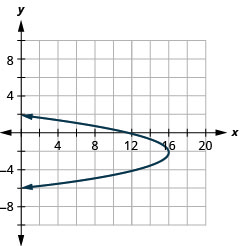
Figura 11.2.58

Exercício$\PageIndex{8}$

Faça um gráfico$x=-y^{2}+2 y-3$ usando propriedades.

Resposta

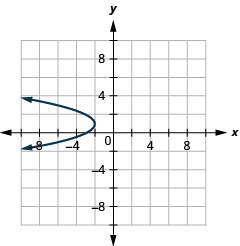
Figura 11.2.59

Na Tabela 11.2.4, vemos a relação entre a equação na forma padrão e as propriedades da parábola. A caixa Como fazer lista as etapas para representar graficamente uma parábola no formato padrão$x=a(y-k)^{2}+h$. Usaremos esse procedimento no próximo exemplo.

Exemplo$\PageIndex{5}$

Gráfico$x=2(y-2)^{2}+1$ usando propriedades.

Solução:

Tabela 11.2.7

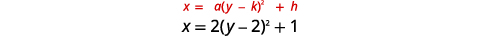Identifique as constantes$a, h, k$.	$a=2, h=1, k=2$
Desde então$a=2$, a parábola se abre para a direita.
O eixo de simetria é$y=k$.	O eixo de simetria é$y=2$.
O vértice é$(h,k)$.	O vértice é$(1,2)$.
Encontre o$x$ -intercept substituindo$y=0$.	$x=2(y-2)^{2}+1$ $x=2(0-2)^{2}+1$ $x=9$
	O$x$ intercepto -é$(9,0)$.
Encontre o ponto simétrico ao$(9,0)$ outro lado do eixo de simetria.	$(9,4)$
Encontre as$y$ interceptações -. Deixe$x=0$.	$\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}$
	Um quadrado não pode ser negativo, então não há uma solução real. Portanto, não há$y$ interceptações.
Faça um gráfico da parábola.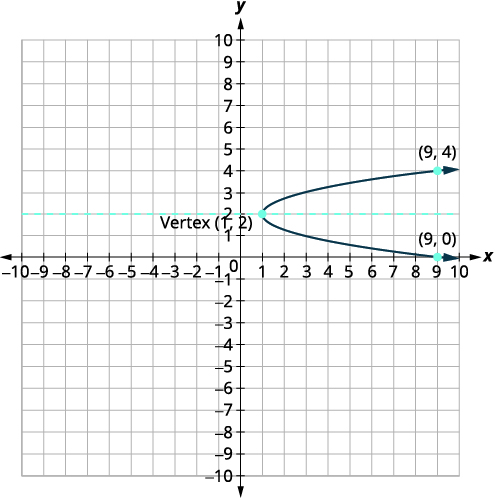

Exercício$\PageIndex{9}$

Gráfico$x=3(y-1)^{2}+2$ usando propriedades.

Resposta

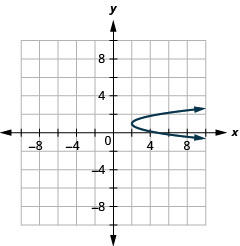
Figura 11.2.63

Exercício$\PageIndex{10}$

Gráfico$x=2(y-3)^{2}+2$ usando propriedades.

Resposta

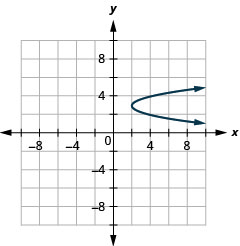
Figura 11.2.64

No próximo exemplo, notamos que a é negativo e, portanto, a parábola se abre para a esquerda.

Exemplo$\PageIndex{6}$

Gráfico$x=-4(y+1)^{2}+4$ usando propriedades.

Solução:

Tabela 11.2.8

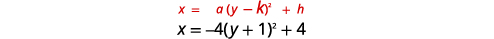Identifique as constantes$a, h, k$.	$a=-4, h=4, k=-1$
Desde então$a=-4$, a parábola se abre para a esquerda.
O eixo de simetria é$y=k$.	O eixo de simetria é$y=-1$.
O vértice é$(h,k)$.	O vértice é$(4,-1)$.
Encontre o$x$ -intercept substituindo$y=0$.	$x=-4(y+1)^{2}+4$ $x=-4(0+1)^{2}+4$ $x=0$
	O$x$ intercepto -é$(0,0)$.
Encontre o ponto simétrico ao$(0,0)$ outro lado do eixo de simetria.	$(0,-2)$
Encontre as$y$ interceptações -.	$x=-4(y+1)^{2}+4$
Deixe$x=0$.	$\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}$
	$y=-1+1 \quad y=-1-1$
	$y=0 \quad\quad y=-2$
	As$y$ interceptações -são$(0,0)$$(0,-2)$ e.
Faça um gráfico da parábola.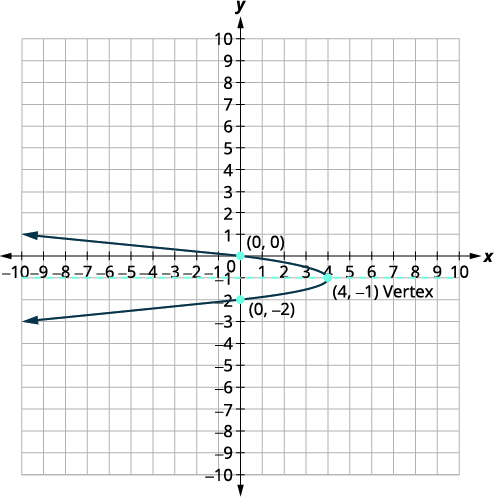

Exercício$\PageIndex{11}$

Gráfico$x=-4(y+2)^{2}+4$ usando propriedades.

Resposta

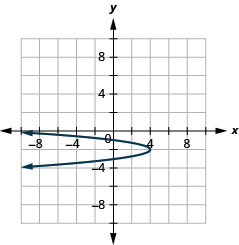
Figura 11.2.68

Exercício$\PageIndex{12}$

Gráfico$x=-2(y+3)^{2}+2$ usando propriedades.

Resposta

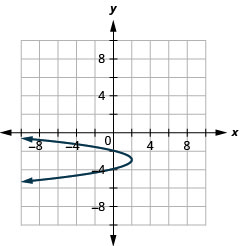
Figura 11.2.69

O próximo exemplo exige que primeiro coloquemos a equação na forma padrão e depois usemos as propriedades.

Exemplo$\PageIndex{7}$

Escreva$x=2 y^{2}+12 y+17$ na forma padrão e, em seguida, use as propriedades da forma padrão para representar graficamente a equação.

Solução:

Tabela 11.2.9

	$x=2 y^{2}+12 y+17$
Reescreva a função na$x=a(y-k)^{2}+h$ forma completando o quadrado.	$x=2\left(y^{2}+6 y\right)+17$
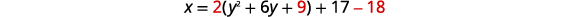	$x=2(y+3)^{2}-1$
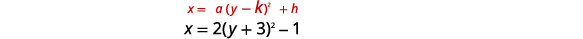Identifique as constantes$a, h, k$.	$a=2, h=-1, k=-3$
Desde então$a=2$, a parábola se abre para a direita.
O eixo de simetria é$y=k$.	O eixo de simetria é$y=-3$.
O vértice é$(h,k)$.	O vértice é$(-1,-3)$.
Encontre o$x$ -intercept substituindo$y=0$.	$x=2(y+3)^{2}-1$ $x=2(0+3)^{2}-1$ $x=17$
	O$x$ intercepto -é$(17,0)$.
Encontre o ponto simétrico ao$(17,0)$ outro lado do eixo de simetria.	$(17,-6)$
Encontre as$y$ interceptações -. Deixe$x=0$.	$\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}$
	$y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}$
	$y \approx-2.3 \quad y \approx-3.7$
	As$y$ interceptações -são$\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)$.
Faça um gráfico da parábola.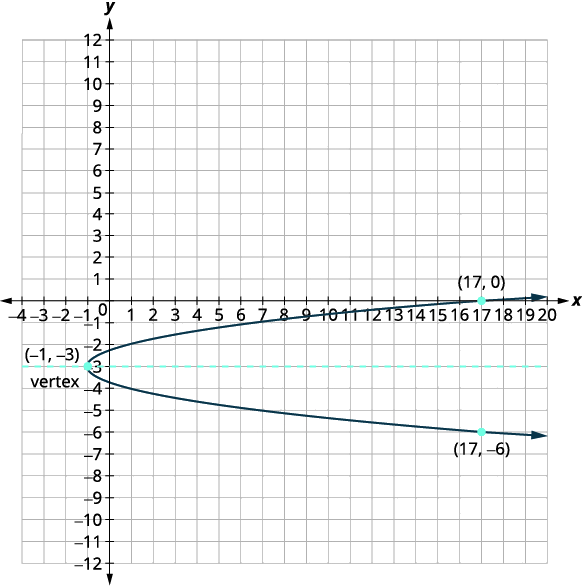

Exercício$\PageIndex{13}$

1. Escreva$x=3 y^{2}+6 y+7$ em formato padrão e
2. Use as propriedades da forma padrão para representar graficamente a equação.

Resposta

1. $x=3(y+1)^{2}+4$
2.  

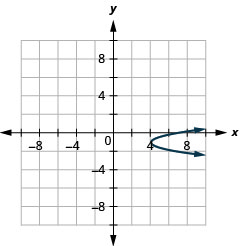
Figura 11.2.77

Exercício$\PageIndex{14}$

1. Escreva$x=-4 y^{2}-16 y-12$ em formato padrão e
2. Use as propriedades da forma padrão para representar graficamente a equação.

Resposta

1. $x=-4(y+2)^{2}+4$
2.  

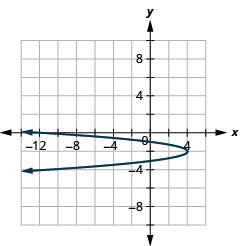
Figura 11.2.78

Resolva aplicativos com Parabolas

Muitos projetos arquitetônicos incorporam parábolas. Não é incomum que pontes sejam construídas usando parábolas, como veremos no próximo exemplo.

Exemplo$\PageIndex{8}$

Encontre a equação do arco parabólico formado na base da ponte mostrada. Escreva a equação na forma padrão.

Figura 11.2.79

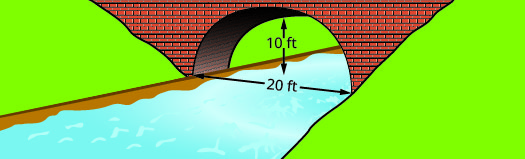
Solução:

Primeiro, configuraremos um sistema de coordenadas e desenharemos a parábola. O gráfico nos dará as informações de que precisamos para escrever a equação do gráfico na forma padrão$y=a(x-h)^{2}+k$.

Tabela 11.2.10

Deixe que o lado inferior esquerdo da ponte seja a origem da grade de coordenadas no ponto$(0,0)$. Como a base tem$20$ pés de largura, o ponto$(20,0)$ representa o lado inferior direito. A ponte tem 10 pés de altura no ponto mais alto. O ponto mais alto é o vértice da parábola, então será a$y$ coordenada -do vértice$10$. Como a ponte é simétrica, o vértice deve ficar a meio caminho entre o ponto mais à esquerda e o ponto mais à direita$(20,0)$.$(0,0)$ A partir disso, sabemos que a$x$ coordenada -do vértice também será$10$.
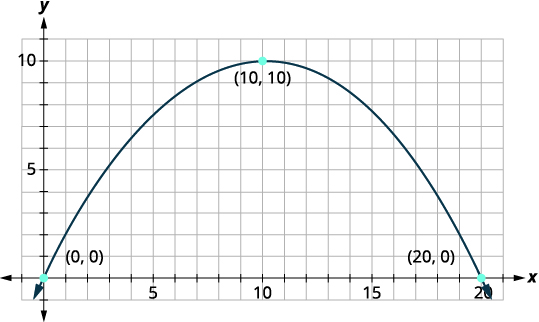Identifique o vértice,$(h,k)$.	$(h, k)=(10,10)$
	$h=10, \quad k=10$
Substitua os valores no formulário padrão. O valor de ainda$a$ é desconhecido. Para encontrar o valor de,$a$ use um dos outros pontos da parábola.	$\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}$
Substitua os valores do outro ponto na equação.	$y=a(x-10)^{2}+10$ $0=a(0-10)^{2}+10$
Resolva para$a$.	$\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}$
	$y=a(x-10)^{2}+10$
Substitua o valor por$a$ na equação.	$y=-\dfrac{1}{10}(x-10)^{2}+10$

Exercício$\PageIndex{15}$

Encontre a equação do arco parabólico formado na base da ponte mostrada. Escreva a equação na forma padrão.

Figura 11.2.81

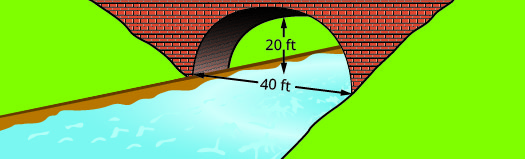
Resposta

$y=-\dfrac{1}{20}(x-20)^{2}+20$

Exercício$\PageIndex{16}$

Encontre a equação do arco parabólico formado na base da ponte mostrada. Escreva a equação na forma padrão.

Figura 11.2.82

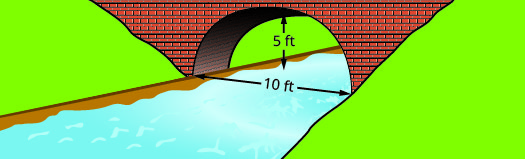
Resposta

$y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5$

Acesse esses recursos on-line para obter instruções adicionais e praticar com funções quadráticas e parábolas.

• Funções quadráticas
• Introdução às cónicas e à representação gráfica de parábolas horizontais

Conceitos-chave

• Parábola: Uma parábola são todos os pontos em um plano que estão à mesma distância de um ponto fixo e de uma linha fixa. O ponto fixo é chamado de foco e a linha fixa é chamada de diretriz da parábola.

Parábolas verticais

Tabela 11.2.1

	Formulário geral $y=a x^{2}+b x+c$	Formulário padrão $y=a(x-h)^{2}+k$
Orientação	\ (y=a x^ {2} +b x+c\) "> para$a>0$ cima;$a<0$ para baixo	\ (y=a (x-h) ^ {2} +k\) "> para$a>0$ cima;$a<0$ para baixo
Eixo de simetria	\ (y=a x^ {2} +b x+c\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Vértice	\ (y=a x^ {2} +b x+c\) ">Substituir$x=-\dfrac{b}{2 a}$ e resolver por$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-interceptar	\ (y=a x^ {2} +b x+c\) ">Deixe$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Deixe$x=0$
$x$-intercepta	\ (y=a x^ {2} +b x+c\) ">Deixe$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Deixe$y=0$

Figura 11.2.3

• Como representar graficamente parábolas verticais$y=a x^{2}+b x+c$ ou$f(x)=a(x-h)^{2}+k)$ usar propriedades.

1. Determine se a parábola se abre para cima ou para baixo.
2. Encontre o eixo de simetria.
3. Encontre o vértice.
4. Encontre o$y$ intercepto -. Encontre o ponto simétrico ao$y$ intercepto -no eixo de simetria.
5. Encontre as$x$ interceptações -.
6. Faça um gráfico da parábola.

Parábolas horizontais

Tabela 11.2.4

	Formulário geral $x=a y^{2}+b y+c$	Formulário padrão $x=a(y-k)^{2}+h$
Orientação	\ (x=a y^ {2} +b y+c\) ">$a>0$ direita;$a<0$ esquerda	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ direita;$a<0$ esquerda
Eixo de simetria	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Vértice	\ (x=a y^ {2} +b y+c\) ">Substituir$y=-\dfrac{b}{2 a}$ e resolver por$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-intercepta	\ (x=a y^ {2} +b y+c\) ">Deixe$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Deixe$x=0$
$y$-interceptar	\ (x=a y^ {2} +b y+c\) ">Deixe$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Deixe$y=0$

Figura 11.2.30

Representação gráfica de parábolas horizontais

Como representar graficamente parábolas horizontais$x=a y^{2}+b y+c$ ou$x=a(y-k)^{2}+h$ usar propriedades.

1. Determine se a parábola se abre para a esquerda ou para a direita.
2. Encontre o eixo de simetria.
3. Encontre o vértice.
4. Encontre o$x$ intercepto -. Encontre o ponto simétrico ao$x$ intercepto -no eixo de simetria.
5. Encontre as$y$ interceptações -.
6. Faça um gráfico da parábola.

Glossário

parábola

Uma parábola são todos os pontos em um plano que estão à mesma distância de um ponto fixo e de uma linha fixa.