9.3: Resolva equações quadráticas completando o quadrado
- Page ID
- 183574
Ao final desta seção, você poderá:
- Complete o quadrado de uma expressão binomial
- Resolva equações quadráticas do formulário\(x^{2}+bx+c=0\) completando o quadrado
- Resolva equações quadráticas do formulário\(ax^{2}+bx+c=0\) completando o quadrado
Antes de começar, faça este teste de prontidão.
- Expandir:\((x+9)^{2}\).
Se você perdeu esse problema, consulte o Exemplo 5.32. - Fator\(y^{2}-14 y+49\).
Se você perdeu esse problema, consulte o Exemplo 6.9. - Fator\(5 n^{2}+40 n+80\).
Se você perdeu esse problema, consulte o Exemplo 6.14.
Até agora, resolvemos equações quadráticas fatorando e usando a propriedade de raiz quadrada. Nesta seção, resolveremos equações quadráticas por meio de um processo chamado completar o quadrado, que é importante para nosso trabalho posterior com cônicas.
Complete o quadrado de uma expressão binomial
Na última seção, pudemos usar a propriedade de raiz quadrada para resolver a equação\((y-7)^{2}=12\) porque o lado esquerdo era um quadrado perfeito.
\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)
Também resolvemos uma equação na qual o lado esquerdo era um trinômio quadrado perfeito, mas tivemos que reescrevê-lo\((x−k)^{2}\) na forma para usar a propriedade de raiz quadrada.
\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)
O que acontece se a variável não fizer parte de um quadrado perfeito? Podemos usar álgebra para fazer um quadrado perfeito?
Vejamos dois exemplos para nos ajudar a reconhecer os padrões.
\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)
Reafirmamos os padrões aqui para referência.
Se\(a\) e\(b\) forem números reais,
Podemos usar esse padrão para “fazer” um quadrado perfeito.
Começaremos com a expressão\(x^{2}+6 x\). Como há um sinal de mais entre os dois termos, usaremos o\((a+b)^{2}\) padrão,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).
Em última análise, precisamos encontrar o último termo desse trinômio que o tornará um trinômio quadrado perfeito. Para fazer isso, precisaremos encontrar\(b\). Mas primeiro começamos determinando\(a\). Observe que o primeiro termo de\(x^{2}+6x\) é um quadrado,\(x^{2}\). Isso nos diz isso\(a=x\).
Qual número\(b\), quando multiplicado por\(2x\) dá\(6x\)? Teria que ser\(3\), ou seja\(\frac{1}{2}(6)\). Então\(b=3\).
Agora, para completar o trinômio quadrado perfeito, encontraremos o último termo ao quadrado\(b\), que é\(3^{2}=9\).
Agora podemos fatorar.
Então, descobrimos que\(9\) adicionar a\(x^{2}+6 x\) “completa o quadrado” e o escrevemos como\((x+3)^{2}\).
- Identifique\(b\), o coeficiente de\(x\).
- Encontre\(\left(\frac{1}{2} b\right)^{2}\) o número para completar o quadrado.
- Adicione\(\left(\frac{1}{2} b\right)^{2}\) o\(x^{2}+bx\) a.
- Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado.
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado.
- \(x^{2}-26 x\)
- \(y^{2}-9 y\)
- \(n^{2}+\frac{1}{2} n\)
Solução:
uma.
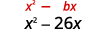 |
|
| O coeficiente de\(x\) é -26. | |
|
Encontre\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\) |
|
| Adicione\(169\) ao binômio para completar o quadrado. |
\(x^{2}-26 x+169\) |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. |
\((x-13)^{2}\) |
b.
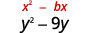 |
|
| O coeficiente de\(y\) é\(-9\). | |
|
Encontre\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\) |
|
| Adicione\(\frac{81}{4}\) ao binômio para completar o quadrado. |
\(y^{2}-9 y+\frac{81}{4}\) |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. |
\(\left(y-\frac{9}{2}\right)^{2}\) |
c.
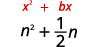 |
|
| O coeficiente de\(n\) é\(\frac{1}{2}\). | |
|
Encontre\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\) |
|
| Adicione\(\frac{1}{16}\) ao binômio para completar o quadrado. | \(n^{2}+\frac{1}{2} n+\frac{1}{16}\) |
| Reescreva como um quadrado binomial. | \(\left(n+\frac{1}{4}\right)^{2}\) |
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado.
- \(a^{2}-20 a\)
- \(m^{2}-5 m\)
- \(p^{2}+\frac{1}{4} p\)
- Resposta
-
- \((a-10)^{2}\)
- \(\left(b-\frac{5}{2}\right)^{2}\)
- \(\left(p+\frac{1}{8}\right)^{2}\)
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado.
- \(b^{2}-4 b\)
- \(n^{2}+13 n\)
- \(q^{2}-\frac{2}{3} q\)
- Resposta
-
- \((b-2)^{2}\)
- \(\left(n+\frac{13}{2}\right)^{2}\)
- \(\left(q-\frac{1}{3}\right)^{2}\)
Resolva equações quadráticas do formulário\(x^{2}+bx+c=0\) completando o quadrado
Ao resolver equações, devemos sempre fazer a mesma coisa nos dois lados da equação. Isso é verdade, é claro, quando resolvemos uma equação quadrática completando o quadrado também. Quando adicionamos um termo a um lado da equação para criar um trinômio quadrado perfeito, também devemos adicionar o mesmo termo ao outro lado da equação.
Por exemplo, se começarmos com a equação\(x^{2}+6x=40\) e quisermos completar o quadrado à esquerda, adicionaremos 9 aos dois lados da equação.
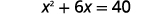 |
|
 |
|
 |
|
| Adicione\(9\) aos dois lados para completar o quadrado. | 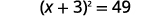 |
Agora, a equação está na forma de resolver usando a propriedade de raiz quadrada! Completar o quadrado é uma forma de transformar uma equação na forma que precisamos para usar a propriedade de raiz quadrada.
Resolva completando o quadrado:\(x^{2}+8x=48\).
Solução:
| Etapa 1: Isole os termos variáveis em um lado e os termos constantes no outro. | Essa equação tem todas as variáveis à esquerda. | \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\) |
| Etapa 2: Encontre\(\left(\frac{1}{2} \cdot b\right)^{2}\) o número para completar o quadrado. Adicione-o aos dois lados da equação. |
Pegue a metade\(8\) e enquadre-a. \(4^{2}=16\) Adicione\(16\) em AMBOS os lados da equação. |
\(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \) \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\) |
| Etapa 3: fatore o trinômio quadrado perfeito como um quadrado binomial. |
\(x^{2}+8 x+16=(x+4)^{2}\) Adicione os termos à direita. |
\((x+4)^{2}=64\) |
| Etapa 4: Use a propriedade Square Root. | \(x+4=\pm \sqrt{64}\) | |
| Etapa 5: Simplifique o radical e resolva as duas equações resultantes. |
\(x+4=\pm 8\) \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\) |
|
| Etapa 6: verifique as soluções. | Coloque cada resposta na equação original para verificar. \(x=4\)Substitua\(x=-12\) e. |
\(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\) \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\) |
Resolva completando o quadrado:\(x^{2}+4 x=5\).
- Resposta
-
\(x=-5, x=-1\)
Resolva completando o quadrado:\(y^{2}−10y=−9\).
- Resposta
-
\(y=1, y=9\)
As etapas para resolver uma equação quadrática completando o quadrado estão listadas aqui.
Resolva uma equação quadrática do formulário\(x^{2}+bx+c=0\) completando o quadrado
- Isole os termos variáveis em um lado e os termos constantes no outro.
- Encontre\(\left(\frac{1}{2} \cdot b\right)^{2}\) o número necessário para completar o quadrado. Adicione-o aos dois lados da equação.
- Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado à esquerda e simplifique adicionando os termos à direita
- Use a propriedade Square Root.
- Simplifique o radical e resolva as duas equações resultantes.
- Verifique as soluções.
Quando resolvemos uma equação completando o quadrado, as respostas nem sempre serão números inteiros.
Resolva completando o quadrado:\(x^{2}+4 x=-21\).
Solução:
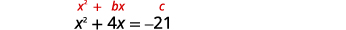 |
|
|
Os termos das variáveis estão no lado esquerdo. Pegue a metade\(4\) e enquadre-a. |
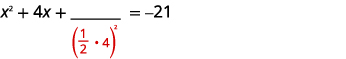 |
| \(\left(\frac{1}{2}(4)\right)^{2}=4\) | |
| Adicione\(4\) aos dois lados. |  |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 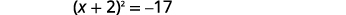 |
| Use a propriedade Square Root. | 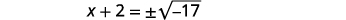 |
| Simplificando o uso de números complexos. | 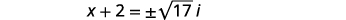 |
| Subtraia\(2\) de cada lado. | 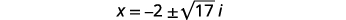 |
| Reescreva para mostrar duas soluções. | 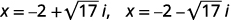 |
| Deixamos o cheque para você. |
Resolva completando o quadrado:\(y^{2}-10 y=-35\).
- Resposta
-
\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)
Resolva completando o quadrado:\(z^{2}+8 z=-19\).
- Resposta
-
\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)
No exemplo anterior, nossas soluções eram números complexos. No próximo exemplo, as soluções serão números irracionais.
Resolva completando o quadrado:\(y^{2}-18 y=-6\).
Solução:
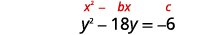 |
|
| Os termos das variáveis estão no lado esquerdo. Pegue a metade\(-18\) e enquadre-a. | |
| \(\left(\frac{1}{2}(-18)\right)^{2}=81\) | 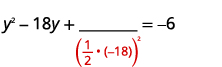 |
| Adicione\(81\) aos dois lados. | 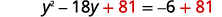 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 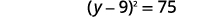 |
| Use a propriedade Square Root. | 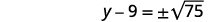 |
| Simplifique o radical. | 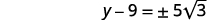 |
| Resolver para\(y\). |  |
|
Verifique. 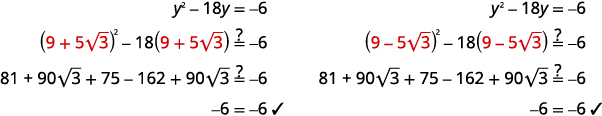
|
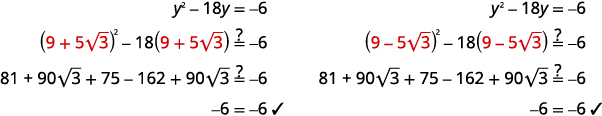 |
Outra forma de verificar isso seria usar uma calculadora. Avalie\(y^{2}−18y\) as duas soluções. A resposta deveria ser\(−6\).
Resolva completando o quadrado:\(x^{2}-16 x=-16\).
- Responda
-
\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)
Resolva completando o quadrado:\(y^{2}+8 y=11\).
- Responda
-
\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)
Começaremos o próximo exemplo isolando os termos variáveis no lado esquerdo da equação.
Resolva completando o quadrado:\(x^{2}+10 x+4=15\).
Solução:
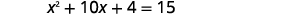 |
|
| Isole os termos variáveis no lado esquerdo. Subtraia\(4\) para obter os termos constantes no lado direito. | 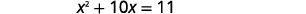 |
| Pegue a metade\(10\) e enquadre-a. | |
| \(\left(\frac{1}{2}(10)\right)^{2}=25\) | 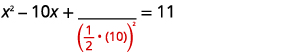 |
| Adicione\(25\) aos dois lados. | 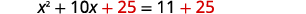 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 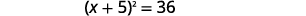 |
| Use a propriedade Square Root. | 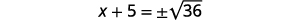 |
| Simplifique o radical. | 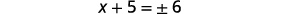 |
| Resolver para\(x\). | 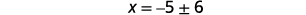 |
| Reescreva para mostrar duas soluções. | 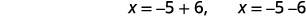 |
| Resolva as equações. | 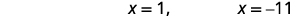 |
|
Confira: 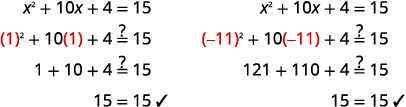
|
Resolva completando o quadrado:\(a^{2}+4 a+9=30\).
- Responda
-
\(a=-7, a=3\)
Resolva completando o quadrado:\(b^{2}+8 b-4=16\).
- Responda
-
\(b=-10, b=2\)
Para resolver a próxima equação, precisamos primeiro coletar todos os termos variáveis no lado esquerdo da equação. Em seguida, procedemos como fizemos nos exemplos anteriores.
Resolva completando o quadrado:\(n^{2}=3 n+11\).
Solução:
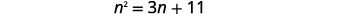 |
|
| Subtraia\(3n\) para obter os termos variáveis no lado esquerdo. |  |
| Pegue a metade\(-3\) e enquadre-a. | |
| \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) | 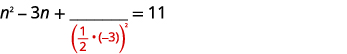 |
| Adicione\(\frac{9}{4}\) aos dois lados. | 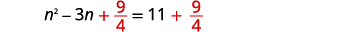 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 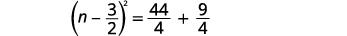 |
| Adicione as frações no lado direito. | 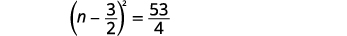 |
| Use a propriedade Square Root. | 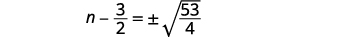 |
| Simplifique o radical. | 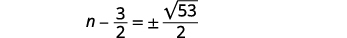 |
| Resolver para\(n\). | 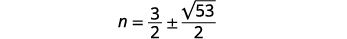 |
| Reescreva para mostrar duas soluções. | 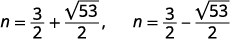 |
|
Confira: Deixamos o cheque para você! |
Resolva completando o quadrado:\(p^{2}=5 p+9\).
- Responda
-
\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)
Resolva completando o quadrado:\(q^{2}=7 q-3\).
- Responda
-
\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)
Observe que o lado esquerdo da próxima equação está na forma fatorada. Mas o lado direito não é zero. Portanto, não podemos usar a Propriedade do Produto Zero, pois ela diz “Se\(a⋅b=0\), então\(a=0\) ou”\(b=0\). Em vez disso, multiplicamos os fatores e, em seguida, colocamos a equação na forma padrão para resolver completando o quadrado.
Resolva completando o quadrado:\((x-3)(x+5)=9\).
Solução:
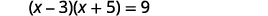 |
|
| Multiplicamos os binômios à esquerda. | 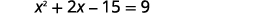 |
| Adicione\(15\) para isolar os termos constantes à direita. | 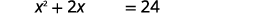 |
| Pegue a metade\(2\) e enquadre-a. | |
| \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) | 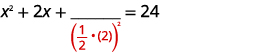 |
| Adicione\(1\) aos dois lados. | 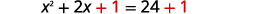 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 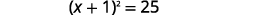 |
| Use a propriedade Square Root. | 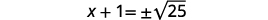 |
| Resolver para\(x\). | 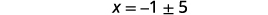 |
| Reescreva para mostrar duas soluções. | 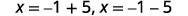 |
| Simplifique. | 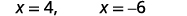 |
|
Confira: Deixamos o cheque para você! |
Resolva completando o quadrado:\((c-2)(c+8)=11\).
- Responda
-
\(c=-9, c=3\)
Resolva completando o quadrado:\((d-7)(d+3)=56\).
- Responda
-
\(d=11, d=-7\)
Resolva equações quadráticas do formulário\(ax^{2}+bx+c=0\) completando o quadrado
O processo de completar o quadrado funciona melhor quando o coeficiente de\(x^{2}\) é\(1\), então o lado esquerdo da equação é da forma\(x^{2}+bx+c\). Se o\(x^{2}\) termo tiver um coeficiente diferente de\(1\), tomamos algumas medidas preliminares para tornar o coeficiente igual\(1\) a.
Às vezes, o coeficiente pode ser calculado a partir de todos os três termos do trinômio. Essa será nossa estratégia no próximo exemplo.
Resolva completando o quadrado:\(3 x^{2}-12 x-15=0\).
Solução:
Para completar o quadrado, precisamos que o coeficiente\(x^{2}\) de seja um. Se considerarmos o coeficiente de\(x^{2}\) como um fator comum, podemos continuar resolvendo a equação completando o quadrado.
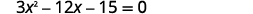 |
|
| Considere o maior fator comum. | 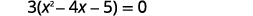 |
| Divida os dois lados por\(3\) para isolar o trinômio com coeficiente\(1\). | 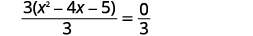 |
| Simplifique. | 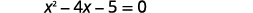 |
| Adicione\(5\) para obter os termos constantes no lado direito. | 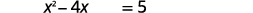 |
| Pegue a metade\(4\) e enquadre-a. | |
| \(\left(\frac{1}{2}(-4)\right)^{2}=4\) | 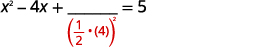 |
| Adicione\(4\) aos dois lados. | 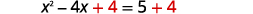 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 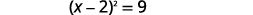 |
| Use a propriedade Square Root. | 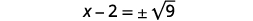 |
| Resolver para\(x\). | 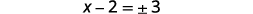 |
| Reescreva para mostrar duas soluções. | 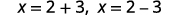 |
| Simplifique. |  |
|
Confira: 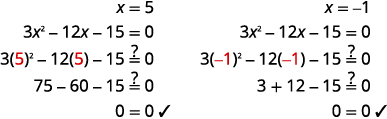
|
Resolva completando o quadrado:\(2 m^{2}+16 m+14=0\).
- Responda
-
\(m=-7, m=-1\)
Resolva completando o quadrado:\(4 n^{2}-24 n-56=8\).
- Responda
-
\(n=-2, n=8\)
Para completar o quadrado, o coeficiente do\(x^{2}\) deve ser\(1\). Quando o coeficiente principal não for um fator de todos os termos, dividiremos os dois lados da equação pelo coeficiente principal! Isso nos dará uma fração para o segundo coeficiente. Já vimos como completar o quadrado com frações nesta seção.
Resolva completando o quadrado:\(2 x^{2}-3 x=20\).
Solução:
Para completar o quadrado, precisamos que o coeficiente\(x^{2}\) de seja um. Dividiremos os dois lados da equação pelo coeficiente de\(x^{2}\). Então, podemos continuar resolvendo a equação completando o quadrado.
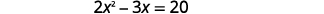 |
|
| Divida os dois lados por\(2\) para obter o coeficiente\(x^{2}\) de ser\(1\). | 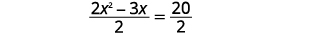 |
| Simplifique. | 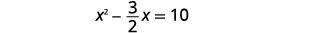 |
| Pegue a metade\(-\frac{3}{2}\) e enquadre-a. | |
| \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) | 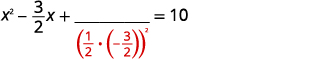 |
| Adicione\(\frac{9}{16}\) aos dois lados. | 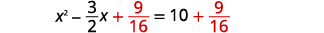 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 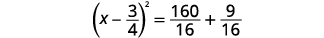 |
| Adicione as frações no lado direito. | 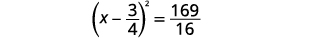 |
| Use a propriedade Square Root. | 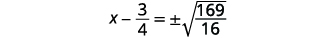 |
| Simplifique o radical. | 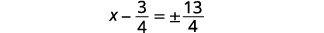 |
| Resolver para\(x\). | 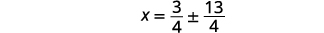 |
| Reescreva para mostrar duas soluções. | 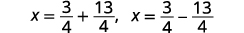 |
| Simplifique. | 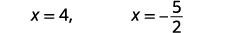 |
|
Confira: Deixamos o cheque para você! |
Resolva completando o quadrado:\(3 r^{2}-2 r=21\).
- Responda
-
\(r=-\frac{7}{3}, r=3\)
Resolva completando o quadrado:\(4 t^{2}+2 t=20\).
- Responda
-
\(t=-\frac{5}{2}, t=2\)
Agora que vimos que o coeficiente de\(x^{2}\) deve ser\(1\) para completarmos o quadrado, atualizamos nosso procedimento para resolver uma equação quadrática completando o quadrado para incluir equações da forma\(a x^{2}+b x+c=0\).
- Divida por aa para criar o coeficiente do\(x^{2}\) termo\(1\).
- Isole os termos variáveis em um lado e os termos constantes no outro.
- Encontre\(\left(\frac{1}{2} \cdot b\right)^{2}\) o número necessário para completar o quadrado. Adicione-o aos dois lados da equação.
- Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado à esquerda e simplifique adicionando os termos à direita
- Use a propriedade Square Root.
- Simplifique o radical e resolva as duas equações resultantes.
- Verifique as soluções.
Resolva completando o quadrado:\(3 x^{2}+2 x=4\).
Solução:
Novamente, nosso primeiro passo será fazer o coeficiente de\(x^{2}\) um. Ao dividir os dois lados da equação pelo coeficiente de\(x^{2}\), podemos então continuar resolvendo a equação completando o quadrado.
 |
|
| Divida os dois lados por\(3\) para que o coeficiente\(x^{2}\) seja igual\(1\). | 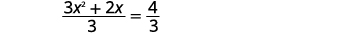 |
| Simplifique. |  |
| Pegue a metade\(\frac{2}{3}\) e enquadre-a. | |
| \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) | 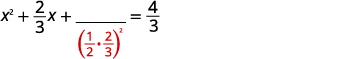 |
| Adicione\(\frac{1}{9}\) aos dois lados. | 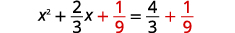 |
| Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado. | 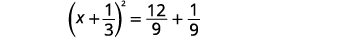 |
| Use a propriedade Square Root. | 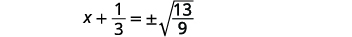 |
| Simplifique o radical. | 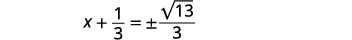 |
| Resolver para\(x\). | 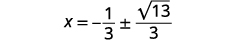 |
| Reescreva para mostrar duas soluções. | 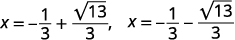 |
|
Confira: Deixamos o cheque para você! |
Resolva completando o quadrado:\(4 x^{2}+3 x=2\).
- Responda
-
\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)
Resolva completando o quadrado:\(3 y^{2}-10 y=-5\).
- Responda
-
\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)
Acesse esses recursos on-line para obter instruções adicionais e praticar a conclusão do quadrado.
Conceitos-chave
- Padrão de quadrados binomiais
Se\(a\) e\(b\) forem números reais,
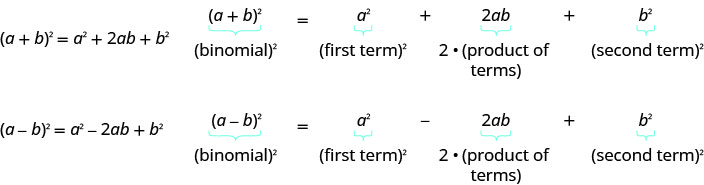
- Como completar um quadrado
- Identifique\(b\), o coeficiente de\(x\).
- Encontre\(\left(\frac{1}{2} b\right)^{2}\) o número para completar o quadrado.
- Adicione o\(\left(\frac{1}{2} b\right)^{2}\) ao\(x^{2}+bx\)
- Reescreva o trinômio como um quadrado binomial
- Como resolver uma equação quadrática do formulário \(a x^{2}+b x+c=0\)completando o quadrado.
- Divida por\(a\) para criar o coeficiente do\(x^{2}\) termo\(1\).
- Isole os termos variáveis em um lado e os termos constantes no outro.
- Encontre\(\left(\frac{1}{2} \cdot b\right)^{2}\) o número necessário para completar o quadrado. Adicione-o aos dois lados da equação.
- Considere o trinômio quadrado perfeito, escrevendo-o como um binômio quadrado à esquerda e simplifique adicionando os termos à direita.
- Use a propriedade Square Root.
- Simplifique o radical e resolva as duas equações resultantes.
- Verifique as soluções.


