Skip to main content
Global

8.9E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183469

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Exercícios 1 a 4: Avalie a raiz quadrada de um número negativo

    Nos exercícios a seguir, escreva cada expressão em termos de\(i\) e simplifique, se possível.

    1. a.\(\sqrt{-16}\) b.\(\sqrt{-11}\) c.\(\sqrt{-8}\)
    2. a.\(\sqrt{-121}\) b.\(\sqrt{-1}\) c.\(\sqrt{-20}\)
    3. a.\(\sqrt{-100}\) b.\(\sqrt{-13}\) c.\(\sqrt{-45}\)
    4. a.\(\sqrt{-49}\) b.\(\sqrt{-15}\) c.\(\sqrt{-75}\)
    Responda

    1. a.\(4i\) b.\(i\sqrt{11}\) c.\(2i\sqrt{2}\)

    3. a.\(10i\) b.\(i\sqrt{13}\) c.\(3i\sqrt{5}\)

    Exercícios 5 - 21: Adicionar ou subtrair números complexos

    Nos exercícios a seguir, adicione ou subtraia, colocando a resposta em\(a + bi\) forma.

    5. \(\sqrt{-75}+\sqrt{-48}\)

    6. \(\sqrt{-12}+\sqrt{-75}\)

    7. \(\sqrt{-50}+\sqrt{-18}\)

    8. \(\sqrt{-72}+\sqrt{-8}\)

    9. \((1+3 i)+(7+4 i)\)

    10. \((6+2 i)+(3-4 i)\)

    11. \((8-i)+(6+3 i)\)

    12. \((7-4 i)+(-2-6 i)\)

    13. \((1-4 i)-(3-6 i)\)

    14. \((8-4 i)-(3+7 i)\)

    15. \((6+i)-(-2-4 i)\)

    16. \((-2+5 i)-(-5+6 i)\)

    17. \((5-\sqrt{-36})+(2-\sqrt{-49})\)

    18. \((-3+\sqrt{-64})+(5-\sqrt{-16})\)

    19. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)

    20. \((-5+\sqrt{-27})-(-4-\sqrt{-48})\)

    Responda

    5. \(0+\left(9\sqrt{3}\right)i\)

    7. \(0+\left(8\sqrt{2}\right)i\)

    9. \(8+7i\)

    11. \(14+2i\)

    13. \(-2+2i\)

    15. \(8+5i\)

    17. \(7-13i\)

    19. \(25-\left(2 \sqrt{2}\right) i\)

    Exercícios 21 - 28: Multiplique números complexos

    Nos exercícios a seguir, multiplique, colocando a resposta em\(a+bi\) forma.

    21. \(4 i(5-3 i)\)

    22. \(2 i(-3+4 i)\)

    23. \(-6 i(-3-2 i)\)

    24. \(-i(6+5 i)\)

    25. \((4+3 i)(-5+6 i)\)

    26. \((-2-5 i)(-4+3 i)\)

    27. \((-3+3 i)(-2-7 i)\)

    28. \((-6-2 i)(-3-5 i)\)

    Responda

    21. \(12+20i\)

    23. \(-12+18i\)

    25. \(-38+9 i\)

    27. \(27+15i\)

    Exercícios 29 - 32: Multiplique números complexos

    Nos exercícios a seguir, multiplique usando o Produto do Padrão de Quadrados Binomiais, colocando a resposta em\(a+bi\) forma.

    29. \((3+4 i)^{2}\)

    30. \((-1+5 i)^{2}\)

    31. \((-2-3 i)^{2}\)

    32. \((-6-5 i)^{2}\)

    Responda

    29. \(-7+24i\)

    31. \(-5-12i\)

    Exercícios 33 a 46: Multiplicar números complexos

    Nos exercícios a seguir, multiplique, colocando a resposta em\(a+bi\) forma.

    33. \(\sqrt{-25} \cdot \sqrt{-36}\)

    34. \(\sqrt{-4} \cdot \sqrt{-16}\)

    35. \(\sqrt{-9} \cdot \sqrt{-100}\)

    36. \(\sqrt{-64} \cdot \sqrt{-9}\)

    37. \((-2-\sqrt{-27})(4-\sqrt{-48})\)

    38. \((5-\sqrt{-12})(-3+\sqrt{-75})\)

    39. \((2+\sqrt{-8})(-4+\sqrt{-18})\)

    40. \((5+\sqrt{-18})(-2-\sqrt{-50})\)

    41. \((2-i)(2+i)\)

    42. \((4-5 i)(4+5 i)\)

    43. \((7-2 i)(7+2 i)\)

    44. \((-3-8 i)(-3+8 i)\)

    Responda

    33. \(30i = 0 + 30i\)

    35. \(-30 = -30 + 0i\)

    37. \(-44+\left(4 \sqrt{3}\right) i\)

    39. \(-20-\left(2 \sqrt{2}\right) i\)

    41. \(5 = 5 + 0i\)

    43. \(53 = 53 + 0i\)

    Exercícios 45 - 49: Multiplique números complexos

    Nos exercícios a seguir, multiplique usando o Padrão Produto de Conjugados Complexos.

    45. \((7-i)(7+i)\)

    46. \((6-5 i)(6+5 i)\)

    47. \((9-2 i)(9+2 i)\)

    48. \((-3-4 i)(-3+4 i)\)

    Responda

    45. \(50\)

    47. \(85\)

    Exercícios 49 - 60: Divida números complexos

    Nos exercícios a seguir, divida, colocando a resposta em\(a+bi\) forma.

    49. \(\dfrac{3+4 i}{4-3 i}\)

    50. \(\dfrac{5-2 i}{2+5 i}\)

    51. \(\dfrac{2+i}{3-4 i}\)

    52. \(\dfrac{3-2 i}{6+i}\)

    53. \(\dfrac{3}{2-3 i}\)

    54. \(\dfrac{2}{4-5 i}\)

    55. \(\dfrac{-4}{3-2 i}\)

    56. \(\dfrac{-1}{3+2 i}\)

    57. \(\dfrac{1+4 i}{3 i}\)

    58. \(\dfrac{4+3 i}{7 i}\)

    59. \(\dfrac{-2-3 i}{4 i}\)

    60. \(\dfrac{-3-5 i}{2 i}\)

    Responda

    49. \(i = 0 + i\)

    51. \(\frac{2}{25}+\frac{11}{25} i\)

    53. \(\frac{6}{13}+\frac{9}{13} i\)

    55. \(-\frac{12}{13}-\frac{8}{13} i\)

    57. \(\frac{4}{3}-\frac{1}{3} i\)

    59. \(-\frac{3}{4}+\frac{1}{2} i\)

    Exercícios 61 - 68: Simplifique os poderes do\(i\)

    Nos exercícios a seguir, simplifique.

    61. \(i^{41}\)

    62. \(i^{39}\)

    63. \(i^{66}\)

    64. \(i^{48}\)

    65. \(i^{128}\)

    66. \(i^{162}\)

    67. \(i^{137}\)

    68. \(i^{255}\)

    Responda

    61. \(i^{41} = i^{40}\cdot i = \left(i^{4}\right)^{10}\cdot i= i\)

    63. \(i^{66} = i^{64}\cdot i^{2} = \left(i^{4}\right)^{16}\cdot (-1)= -1\)

    65. \(i^{128} = \left(i^{4}\right)^{32} = 1\)

    67. \(i^{137} = i^{136}\cdot i = \left(i^{4}\right)^{34}\cdot i = 1 \cdot i = i\)

    Exercícios 69 - 72: Exercícios de escrita

    69. Explique a relação entre números reais e números complexos.

    70. Aniket multiplicou da seguinte forma e recebeu a resposta errada. O que há de errado com seu raciocínio?
    \(\begin{array}{c}{\sqrt{-7} \cdot \sqrt{-7}} \\ {\sqrt{49}} \\ {7}\end{array}\)

    71. Por que é\(\sqrt{-64}=8 i\), mas\(\sqrt[3]{-64}=-4\).

    72. Explique como dividir números complexos é semelhante à racionalização de um denominador.

    Responda

    69. As respostas podem variar

    71. As respostas podem variar

    Verificação automática

    a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

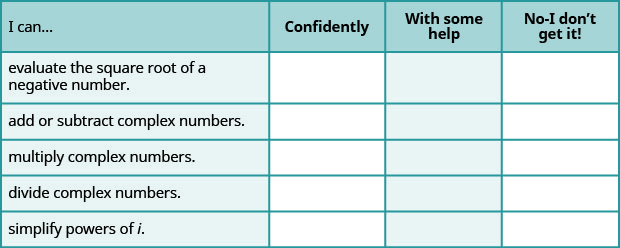
    A tabela tem 4 colunas e 4 linhas. A primeira linha é uma linha de cabeçalho com os cabeçalhos “Eu posso”, “Confidentemente”, “com alguma ajuda.—, e “Não”” Eu não entendo!™ â€. A primeira coluna contém as frases “avaliar a raiz quadrada de um número negativo”, “adicionar ou subtrair números complexos”, “multiplicar números complexos”, “dividir números complexos” e “simplificar as potências de i—. As outras colunas são deixadas em branco para que o aluno possa indicar seu nível de compreensão.
    Figura 8.8.15

    b. Em uma escala de 1 a 10, como você classificaria seu domínio desta seção à luz de suas respostas na lista de verificação? Como você pode melhorar isso?