8.9: Use o Sistema de Números Complexos
- Page ID
- 183457
Ao final desta seção, você poderá:
- Avalie a raiz quadrada de um número negativo
- Adicione e subtraia números complexos
- Multiplique números complexos
- Divida números complexos
- Simplifique os poderes do\(i\)
Antes de começar, faça este teste de prontidão.
- Dados os números\(-4,-\sqrt{7}, 0 . \overline{5}, \frac{7}{3}, 3, \sqrt{81}\), liste os
- números racionais
- números irracionais
- números reais
Se você perdeu esse problema, consulte o Exemplo 1.42.
- Multiplique:\((x−3)(2x+5)\).
Se você perdeu esse problema, consulte o Exemplo 5.28. - Racionalize o denominador:\(\frac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}\)
Se você perdeu esse problema, consulte o Exemplo 5.32.
Avalie a raiz quadrada de um número negativo
Sempre que temos uma situação em que temos uma raiz quadrada de um número negativo, dizemos que não há um número real igual a essa raiz quadrada. Por exemplo, para simplificar\(\sqrt{-1}\), estamos procurando um número real\(x\) para que\(x^{2}=-1\). Como todos os números reais ao quadrado são números positivos, não há número real igual\(–1\) ao quadrado.
Os matemáticos muitas vezes expandiram seus sistemas numéricos conforme necessário. Eles adicionaram\(0\) os números de contagem para obter os números inteiros. Quando precisavam de saldos negativos, eles adicionavam números negativos para obter os números inteiros. Quando precisaram da ideia de partes de um todo, eles adicionaram frações e obtiveram os números racionais. A adição de números irracionais permitiu números como\(\sqrt{5}\). Tudo isso junto nos deu os números reais e, até agora, em seu estudo de matemática, isso tem sido suficiente.
Mas agora vamos expandir os números reais para incluir as raízes quadradas dos números negativos. Começamos definindo a unidade imaginária\(i\) como o número cujo quadrado é\(–1\).
Definição\(\PageIndex{1}\)
A unidade imaginária\(i\) é o número cujo quadrado é\(-1\).
\(i^{2}=-1 \text { or } i=\sqrt{-1}\)
Usaremos a unidade imaginária para simplificar as raízes quadradas dos números negativos.
Definição\(\PageIndex{2}\)
Raiz quadrada de um número negativo
Se\(b\) for um número real positivo, então
\(\sqrt{-b}=\sqrt{b} i\)
Usaremos essa definição no próximo exemplo. Tenha cuidado para que fique claro que o não\(i\) está sob o radical. Às vezes, você verá isso escrito\(\sqrt{-b}=i \sqrt{b}\) para enfatizar que não\(i\) está sob o radical. Mas o\(\sqrt{-b}=\sqrt{b} i\) é considerado um formulário padrão.
Escrever cada expressão em termos de\(i\) e simplificar é possível:
- \(\sqrt{-25}\)
- \(\sqrt{-7}\)
- \(\sqrt{-12}\)
Solução:
uma.
\(\sqrt{-25}\)
Use a definição da raiz quadrada dos números negativos.
\(\sqrt{25} i\)
Simplifique.
\(5i\)
b.
\(\sqrt{-7}\)
Use a definição da raiz quadrada dos números negativos.
\(\sqrt{7} i\)
Simplifique.
Tenha cuidado para que fique claro que não\(i\) está sob o signo radical.
c.
\(\sqrt{-12}\)
Use a definição da raiz quadrada dos números negativos.
\(\sqrt{12} i\)
Simplifique\(\sqrt{12}\).
\(2 \sqrt{3} i\)
Escreva cada expressão em termos de\(i\) e simplifique, se possível:
- \(\sqrt{-81}\)
- \(\sqrt{-5}\)
- \(\sqrt{-18}\)
- Resposta
-
- \(9i\)
- \(\sqrt{5} i\)
- \(3 \sqrt{2} i\)
Escreva cada expressão em termos de\(i\) e simplifique, se possível:
- \(\sqrt{-36}\)
- \(\sqrt{-3}\)
- \(\sqrt{-27}\)
- Resposta
-
- \(6i\)
- \(\sqrt{3} i\)
- \(3\sqrt{3} i\)
Agora que estamos familiarizados com o número imaginário\(i\), podemos expandir os números reais para incluir números imaginários. O sistema numérico complexo inclui os números reais e os números imaginários. Um número complexo é do formato\(a+bi\), onde\(a, b\) estão os números reais. Chamamos\(a\) a parte real e\(b\) a parte imaginária.
Definição\(\PageIndex{3}\)
Um número complexo tem a forma\(a+bi\), onde\(a\) e\(b\) são números reais.
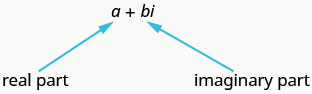
Um número complexo está na forma padrão quando escrito como\(a+bi\), onde\(a\) e\(b\) são números reais.
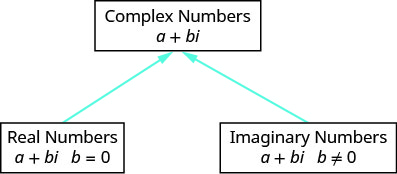
Se\(b=0\), então\(a+bi\) se torna\(a+0⋅i=a\) e é um número real.
Se\(b≠0\), então\(a+bi\) é um número imaginário.
Se\(a=0\), então\(a+bi\) se torna\(0+bi=bi\) e é chamado de número imaginário puro.
Resumimos isso aqui.
| \(a+bi\) | ||
| \(b=0\) |
\(a+0 \cdot i\) \(a\) |
Número real |
| \(b\neq 0\) | \(a+bi\) | Número imaginário |
| \(a=0\)R |
\(0+bi\) \(bi\) |
Número imaginário puro 4 |
A forma padrão de um número complexo é\(a+bi\), então isso explica por que a forma preferida é\(\sqrt{-b}=\sqrt{b} i\) quando\(b>0\).
O diagrama nos ajuda a visualizar o complexo sistema numérico. É composto tanto pelos números reais quanto pelos números imaginários.
Adicionar ou subtrair números complexos
Agora estamos prontos para realizar as operações de adição, subtração, multiplicação e divisão nos números complexos, assim como fizemos com os números reais.
Adicionar e subtrair números complexos é muito parecido com adicionar ou subtrair termos semelhantes. Somamos ou subtraímos as partes reais e, em seguida, adicionamos ou subtraímos as partes imaginárias. Nosso resultado final deve estar na forma padrão.
Adicionar:\(\sqrt{-12}+\sqrt{-27}\).
Solução:
\(\sqrt{-12}+\sqrt{-27}\)
Use a definição da raiz quadrada dos números negativos.
\(\sqrt{12} i+\sqrt{27} i\)
Simplifique as raízes quadradas.
\(2 \sqrt{3} i+3 \sqrt{3} i\)
Adicionar.
\(5 \sqrt{3} i\)
Adicionar:\(\sqrt{-8}+\sqrt{-32}\).
- Resposta
-
\(6 \sqrt{2} i\)
Adicionar:\(\sqrt{-27}+\sqrt{-48}\)
- Resposta
-
\(7 \sqrt{3} i\)
Lembre-se de adicionar as partes reais e as partes imaginárias neste próximo exemplo.
Simplifique:
- \((4-3 i)+(5+6 i)\)
- \((2-5 i)-(5-2 i)\)
Solução:
uma.
\((4-3 i)+(5+6 i)\)
Use a Propriedade Associativa para juntar as partes reais e as partes imaginárias.
\((4+5)+(-3 i+6 i)\)
Simplifique.
\(9+3i\)
b.
\((2-5 i)-(5-2 i)\)
Distribuir.
\(2-5 i-5+2 i\)
Use a Propriedade Associativa para juntar as partes reais e as partes imaginárias.
\(2-5-5 i+2 i\)
Simplifique.
\(-3-3 i\)
Simplifique:
- \((2+7 i)+(4-2 i)\)
- \((8-4 i)-(2-i)\)
- Resposta
-
- \(6+5i\)
- \(6-3i\)
Simplifique:
- \((3-2 i)+(-5-4 i)\)
- \((4+3 i)-(2-6 i)\)
- Resposta
-
- \(-2-6i\)
- \(2+9i\)
Multiplique números complexos
Multiplicar números complexos também é muito parecido com multiplicar expressões com coeficientes e variáveis. Há apenas um caso especial que precisamos considerar. Veremos isso depois de praticarmos nos próximos dois exemplos.
Multiplique:\(2 i(7-5 i)\)
Solução:
\(2 i(7-5 i)\)
Distribuir.
\(14 i-10 i^{2}\)
Simplifique\(i^{2}\).
\(14 i-10(-1)\)
Multiplique.
\(14 i+10\)
Escreva em formato padrão.
\(10+14i\)
Multiplique:\(4 i(5-3 i)\).
- Resposta
-
\(12+20i\)
Multiplique:\(-3 i(2+4 i)\).
- Resposta
-
\(12-6i\)
No próximo exemplo, multiplicamos os binômios usando a Propriedade Distributiva ou FOIL.
Multiplique:\((3+2 i)(4-3 i)\).
Solução:
\((3+2 i)(4-3 i)\)
Use FOIL.
\(12-9 i+8 i-6 i^{2}\)
Simplifique\(i^{2}\) e combine termos semelhantes.
\(12-i-6(-1)\)
Multiplique.
\(12-i+6\)
Combine as partes reais.
\(18-i\)
Múltiplo:\((5-3 i)(-1-2 i)\).
- Resposta
-
\(-11-7i\)
Múltiplo:\((-4-3 i)(2+i)\).
- Resposta
-
\(-5-10i\)
No próximo exemplo, poderíamos usar FOIL ou o padrão Product of Binomial Squares.
Multiplique:\((3+2 i)^{2}\)
Solução:
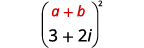 |
|
| Use o produto do padrão de quadrados binomiais,\((a+b)^{2}=a^{2}+2 a b+b^{2}\). |  |
| Simplifique. | 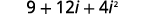 |
| Simplifique\(i^{2}\). | 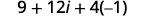 |
| Simplifique. | 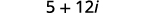 |
Multiplique usando o padrão de quadrados binomiais:\((-2-5 i)^{2}\).
- Resposta
-
\(-21+20 i\)
Multiplique usando o padrão de quadrados binomiais:\((-5+4 i)^{2}\).
- Resposta
-
\(9-40i\)
Como a raiz quadrada de um número negativo não é um número real, não podemos usar a propriedade do produto para radicais. Para multiplicar raízes quadradas de números negativos, devemos primeiro escrevê-las como números complexos, usando\(\sqrt{-b}=\sqrt{b}i\) .Este é um lugar em que os alunos tendem a cometer erros, então tenha cuidado ao ver a multiplicação por uma raiz quadrada negativa.
Multiplique:\(\sqrt{-36} \cdot \sqrt{-4}\).
Solução:
Para multiplicar raízes quadradas de números negativos, primeiro as escrevemos como números complexos.
\(\sqrt{-36} \cdot \sqrt{-4}\)
Escreva como números complexos usando\(\sqrt{-b}=\sqrt{b}i\).
\(\sqrt{36} i \cdot \sqrt{4} i\)
Simplifique.
\(6 i \cdot 2 i\)
Multiplique.
\(12i^{2}\)
Simplifique\(i^{2}\) e multiplique.
\(-12\)
Multiplique:\(\sqrt{-49} \cdot \sqrt{-4}\).
- Resposta
-
\(-14\)
Multiplique:\(\sqrt{-36} \cdot \sqrt{-81}\).
- Resposta
-
\(-54\)
No exemplo a seguir, cada binômio tem uma raiz quadrada de um número negativo. Antes de multiplicar, cada raiz quadrada de um número negativo deve ser escrita como um número complexo.
Multiplique:\((3-\sqrt{-12})(5+\sqrt{-27})\).
Solução:
Para multiplicar raízes quadradas de números negativos, primeiro as escrevemos como números complexos.
\((3-\sqrt{-12})(5+\sqrt{-27})\)
Escreva como números complexos usando\(\sqrt{-b}=\sqrt{b}i\).
\((3-2 \sqrt{3} i)(5+3 \sqrt{3} i)\)
Use FOIL.
\(15+9 \sqrt{3} i-10 \sqrt{3} i-6 \cdot 3 i^{2}\)
Combine termos semelhantes e simplifique\(i^{2}\).
\(15-\sqrt{3} i-6 \cdot(-3)\)
Multiplique e combine termos semelhantes.
\(33-\sqrt{3} i\)
Multiplique:\((4-\sqrt{-12})(3-\sqrt{-48})\).
- Resposta
-
\(-12-22 \sqrt{3} i\)
Multiplique:\((-2+\sqrt{-8})(3-\sqrt{-18})\).
- Resposta
-
\(6+12 \sqrt{2} i\)
Examinamos pela primeira vez os pares conjugados quando estudamos os polinômios. Dissemos que um par de binômios, cada um com o mesmo primeiro termo e o mesmo último termo, mas um é uma soma e outro é uma diferença, é chamado de par conjugado e tem a forma\((a−b),(a+b)\).
Um par conjugado complexo é muito semelhante. Para um número complexo do formulário\(a+bi\), seu conjugado é\(a−bi\). Observe que eles têm o mesmo primeiro termo e o mesmo último termo, mas um é uma soma e o outro é uma diferença.
Definição\(\PageIndex{4}\)
Um par complexo de conjugados tem a forma\(a+bi,a-bi\).
Multiplicaremos um par complexo de conjugados no próximo exemplo.
Multiplique:\((3-2 i)(3+2 i)\).
Solução:
\((3-2 i)(3+2 i)\)
Use FOIL
\(9+6 i-6 i-4 i^{2}\)
Combine termos semelhantes e simplifique\(i^{2}\).
\(9-4(-1)\)
Multiplique e combine termos semelhantes.
\(13\)
Multiplique:\((4-3 i) \cdot(4+3 i)\).
- Resposta
-
\(25\)
Multiplique:\((-2+5 i) \cdot(-2-5 i)\).
- Resposta
-
\(29\)
Em nosso estudo de polinômios, sabemos que o produto dos conjugados é sempre da forma\((a-b)(a+b)=a^{2}-b^{2}\). O resultado é chamado de diferença de quadrados. Podemos multiplicar um par complexo de conjugados usando esse padrão.
No último exemplo, usamos FOIL. Agora usaremos o Padrão Produto de Conjugados.
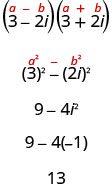
Observe que esse é o mesmo resultado que encontramos no Exemplo 8.8.9.
Quando multiplicamos conjugados complexos, o produto dos últimos termos sempre terá um\(i^{2}\) que simplifica para\(−1\).
\(\begin{array}{c}{(a-b i)(a+b i)} \\ {a^{2}-(b i)^{2}} \\ {a^{2}-b^{2} i^{2}} \\ {a^{2}-b^{2}(-1)} \\ {a^{2}+b^{2}}\end{array}\)
Isso nos leva ao padrão Produto de Conjugados Complexos:\((a-b i)(a+b i)=a^{2}+b^{2}\)
Definição\(\PageIndex{5}\)
Produto de conjugados complexos
Se\(a\) e\(b\) forem números reais, então
\((a-b i)(a+b i)=a^{2}+b^{2}\)
Multiplique usando o padrão Produto de Conjugados Complexos:\((8-2 i)(8+2 i)\).
Solução:
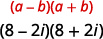 |
|
| Use o padrão Product of Complex Conjugates,\((a-b i)(a+b i)=a^{2}+b^{2}\). | 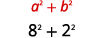 |
| Simplifique os quadrados. | 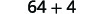 |
| Adicionar. | 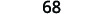 |
Multiplique usando o padrão Produto de Conjugados Complexos:\((3-10 i)(3+10 i)\).
- Resposta
-
\(109\)
Multiplique usando o padrão Produto de Conjugados Complexos:\((-5+4 i)(-5-4 i)\).
- Resposta
-
\(41\)
Divida números complexos
Dividir números complexos é muito parecido com racionalizar um denominador. Queremos que nosso resultado esteja na forma padrão, sem números imaginários no denominador.
Divida:\(\frac{4+3 i}{3-4 i}\).
Solução:
| Etapa 1: Escreva o numerador e o denominador na forma padrão. | Ambos estão em formato padrão. | \(\frac{4+3 i}{3-4 i}\) |
| Etapa 2: Multiplique o numerador e o denominador pelo conjugado complexo do denominador. | O complexo conjugado de\(3-4i\) é\(3+4i\). | \(\frac{(4+3 i)\color{red}{(3+4 i)}}{(3-4 i)\color{red}{(3+4 i)}}\) |
| Etapa 3: Simplifique e escreva o resultado no formato padrão. |
Use o padrão\((a-b i)(a+b i)=a^{2}+b^{2}\) no denominador. Combine termos semelhantes. Simplifique. Escreva o resultado no formato padrão. |
\(\begin{array}{c}{\frac{12+16 i+9 i+12 i^{2}}{9+16}} \\ {\frac{12+25 i-12}{25}} \\ {\frac{25 i}{25}} \\ {i}\end{array}\) |
Divida:\(\frac{2+5 i}{5-2 i}\).
- Resposta
-
\(i\)
Divida:\(\frac{1+6 i}{6-i}\).
- Resposta
-
\(i\)
Resumimos as etapas aqui.
Como dividir números complexos
- Escreva o numerador e o denominador na forma padrão.
- Multiplique o numerador e o denominador pelo conjugado complexo do denominador.
- Simplifique e escreva o resultado no formato padrão.
Divida, escrevendo as respostas na forma padrão:\(\frac{-3}{5+2 i}\).
Solução:
\(\frac{-3}{5+2 i}\)
Multiplique o numerador e o denominador pelo conjugado complexo do denominador.
\(\frac{-3(5-2 i)}{(5+2 i)(5-2 i)}\)
Multiplique no numerador e use o Padrão Produto de Conjugados Complexos no denominador.
\(\frac{-15+6 i}{5^{2}+2^{2}}\)
Simplifique.
\(\frac{-15+6 i}{29}\)
Escreva em formato padrão.
\(-\frac{15}{29}+\frac{6}{29} i\)
Divida, escrevendo a resposta na forma padrão:\(\frac{4}{1-4 i}\).
- Resposta
-
\(\frac{4}{17}+\frac{16}{17} i\)
Divida, escrevendo a resposta na forma padrão:\(\frac{-2}{-1+2 i}\).
- Resposta
-
\(\frac{2}{5}+\frac{4}{5} i\)
Tenha cuidado ao encontrar o conjugado do denominador.
Divida:\(\frac{5+3 i}{4 i}\).
Solução:
\(\frac{5+3 i}{4 i}\)
Escreva o denominador na forma padrão.
\(\frac{5+3 i}{0+4 i}\)
Multiplique o numerador e o denominador pelo conjugado complexo do denominador.
\(\frac{(5+3 i)(0-4 i)}{(0+4 i)(0-4 i)}\)
Simplifique.
\(\frac{(5+3 i)(-4 i)}{(4 i)(-4 i)}\)
Multiplique.
\(\frac{-20 i-12 i^{2}}{-16 i^{2}}\).
Simplifique\(i^{2}\) o.
\(\frac{-20 i+12}{16}\)
Reescreva no formato padrão.
\(\frac{12}{16}-\frac{20}{16} i\)
Simplifique as frações.
\(\frac{3}{4}-\frac{5}{4} i\)
Divida:\(\frac{3+3 i}{2 i}\).
- Resposta
-
\(\frac{3}{2}-\frac{3}{2} i\)
Divida:\(\frac{2+4 i}{5 i}\).
- Resposta
-
\(\frac{4}{5}-\frac{2}{5} i\)
Simplifique os poderes do\(i\)
Os poderes de\(i\) criar um padrão interessante que nos ajudará a simplificar os poderes superiores do\(i\). Vamos avaliar os poderes do\(i\) para ver o padrão.
\(\begin{array}{ccc}{i^{1}} & {i^{2}} & {i^{3}} & {i^{4}} \\ {i} & {-1} & {i^{2}\cdot i} & {i^{2}\cdot i^{2}}\\ {}&{}&{-1\cdot i}&{(-1)(-1)}\\ {}&{}&{-i}&{1}\end{array}\)
\(\begin{array}{cccc}{i^{5}} & {i^{6}} & {i^{7}} & {i^{8}} \\ {i^{4} \cdot i} & {i^{4} \cdot i^{2}} & {i^{4} \cdot i^{3}} & {i^{4} \cdot i^{4}} \\ {1 \cdot i} & {1 \cdot i^{2}} & {1 \cdot i^{3}} & {1 \cdot 1} \\ {i} & {i^{2}} & {i^{3}} & {1} \\ {}&{-1} & {-i}\end{array}\)
Resumimos isso agora.
\(\begin{array}{ll}{i^{1}=i} & {i^{5}=i} \\ {i^{2}=-1} & {i^{6}=-1} \\ {i^{3}=-i} & {i^{7}=-i} \\ {i^{4}=1} & {i^{8}=1}\end{array}\)
Se continuássemos, o padrão continuaria se repetindo em blocos de quatro. Podemos usar esse padrão para nos ajudar a simplificar os poderes do\(i\). Desde então\(i^{4}=1\), reescrevemos cada potência\(i^{n}\),, como um produto usando\(i^{4}\) para uma potência e outra potência de\(i\).
Nós o reescrevemos na forma\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\), onde o expoente\(q\),, é o quociente de\(n\) dividido por\(4\) e o expoente\(r\),, é o restante dessa divisão. Por exemplo, para simplificar\(i^{57}\), dividimos\(57\) por\(4\) e obtemos\(14\) com o restante de\(1\). Em outras palavras,\(57=4⋅14+1\). Então, escrevemos\(i^{57}=\left(1^{4}\right)^{14} \cdot i^{1}\) e depois simplificamos a partir daí.
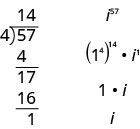
Simplifique:\(i^{86}\).
Solução:
\(i^{86}\)
Divida\(86\) por\(4\) e reescreva\(i^{86}\) no\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\) formulário.
\(\left(1^{4}\right)^{21} \cdot i^{2}\)
Simplifique.
\((1)^{21} \cdot(-1)\)
Simplifique.
\(-1\)
Simplifique:\(i^{74}\).
- Resposta
-
\(-1\)
Simplifique:\(i^{92}\).
- Resposta
-
\(1\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com o complexo sistema numérico.
- Expressando raízes quadradas de números negativos com i
- Subtraia e multiplique números complexos
- Dividindo números complexos
- Reescrevendo os poderes de i
Conceitos-chave
- Raiz quadrada de um número negativo
- Se\(b\) for um número real positivo, então\ (\ sqrt {-b} =\ sqrt {b} i\
| \(a+bi\) | ||
| \(b=0\) |
\(a+0\cdot i\) \(a\) |
Número real |
| \(b\neq 0\) | \(a+bi\) | Número imaginário |
| \(a=0\) |
\(0+bi\) \(bi\) |
Número imaginário puro |
-
- Um número complexo está na forma padrão quando escrito como a + bi, onde a, b são números reais.
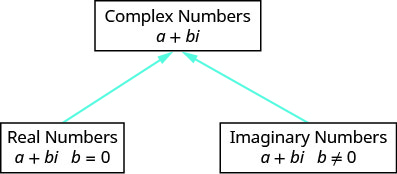
Figura 8.8.2
- Um número complexo está na forma padrão quando escrito como a + bi, onde a, b são números reais.
- Produto de conjugados complexos
- Se\(a, b\) forem números reais, então
\((a−bi)(a+bi)=a^{2}+b^{2}\)
- Se\(a, b\) forem números reais, então
- Como dividir números complexos
- Escreva o numerador e o denominador na forma padrão.
- Multiplique o numerador e o denominador pelo conjugado complexo do denominador.
- Simplifique e escreva o resultado no formato padrão.
Glossário
- par conjugado complexo
- Um par complexo de conjugados tem a forma\(a+bi, a-bi\).
- número complexo
- Um número complexo tem a forma\(a+bi\), onde\(a\) e\(b\) são números reais. Chamamos\(a\) a parte real e\(b\) a parte imaginária.
- sistema numérico complexo
- O sistema numérico complexo é composto tanto pelos números reais quanto pelos números imaginários.
- unidade imaginária
- A unidade imaginária\(i\) é o número cujo quadrado é\(–1\). \(i^{2}=-1\)ou\(i=\sqrt{−1}\).
- formulário padrão
- Um número complexo está na forma padrão quando escrito como\(a+bi\), onde\(a, b\) estão os números reais.


