8.8: Use radicais em funções

Last updated
Save as PDF

Page ID: 183397

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Avalie uma função radical
Encontre o domínio de uma função radical
Grafar funções radicais

Antes de começar, faça este teste de prontidão.

Resolver:$1−2x≥0$.
Se você perdeu esse problema, consulte o Exemplo 2.50.
Para$f(x)=3x−4$, avalie$f(2),f(−1),f(0)$.
Se você perdeu esse problema, revise o Exemplo 3.48.
Gráfico$f(x)=\sqrt{x}$. Declare o domínio e o intervalo da função na notação de intervalo.
Se você perdeu esse problema, revise o Exemplo 3.56.

Avalie uma função radical

Nesta seção, estenderemos nosso trabalho anterior com funções para incluir radicais. Se uma função é definida por uma expressão radical, nós a chamamos de função radical.

A função de raiz quadrada é$f(x)=\sqrt{x}$.
A função raiz cúbica é$f(x)=\sqrt[3]{x}$.

Definição$\PageIndex{1}$: radical function

Uma função radical é uma função definida por uma expressão radical.

Para calcular uma função radical, encontramos o valor de$f(x)$ para um determinado valor,$x$ exatamente como fizemos em nosso trabalho anterior com funções.

Exemplo$\PageIndex{1}$

Para a função$f(x)=\sqrt{2 x-1}$, encontre

$f(5)$
$f(-2)$

Solução:

uma.

$f(x)=\sqrt{2 x-1}$

Para avaliar$f(5)$, substitua$5$ por$x$.

$f(5)=\sqrt{2 \cdot 5-1}$

Simplifique.

$f(5)=\sqrt{9}$

Pegue a raiz quadrada.

$f(5)=3$

$f(x)=\sqrt{2 x-1}$

Para avaliar$f(-2)$, substitua$-2$ por$x$.

$f(-2)=\sqrt{2(-2)-1}$

Simplifique.

$f(-2)=\sqrt{-5}$

Como a raiz quadrada de um número negativo não é um número real, a função não tem um valor em$x=-2$.

Exercício$\PageIndex{1}$

Para a função$f(x)=\sqrt{3 x-2}$, encontre

$f(6)$
$f(0)$

Resposta

$f(6)=4$
nenhum valor em$x=0$

Exercício$\PageIndex{2}$

Para a função$g(x)=\sqrt{5x+5}$, encontre

$g(4)$
$g(-3)$

Resposta

$g(4)=5$
nenhum valor em$f(-3)$

Seguimos o mesmo procedimento para avaliar as raízes cúbicas.

Exemplo$\PageIndex{2}$

Para a função$g(x)=\sqrt[3]{x-6}$, encontre

$g(14)$
$g(-2)$

Solução:

uma.

$g(x)=\sqrt[3]{x-6}$

Para avaliar$g(14)$, substitua$14$ por$x$.

$g(14)=\sqrt[3]{14-6}$

Simplifique.

$g(14)=\sqrt[3]{8}$

Pegue a raiz cúbica.

$g(14)=2$

$g(x)=\sqrt[3]{x-6}$

Para avaliar$g(-2)$, substitua$-2$ por$x$.

$g(-2)=\sqrt[3]{-2-6}$

Simplifique.

$g(-2)=\sqrt[3]{-8}$

Pegue a raiz cúbica.

$g(-2)=-2$

Exercício$\PageIndex{3}$

Para a função$g(x)=\sqrt[3]{3 x-4}$, encontre

$g(4)$
$g(1)$

Resposta

$g(4)=2$
$g(1)=-1$

Exercício$\PageIndex{4}$

Para a função$h(x)=\sqrt[3]{5 x-2}$, encontre

$h(2)$
$h(-5)$

Resposta

$h(2)=2$
$h(-5)=-3$

O próximo exemplo tem uma quarta raiz.

Exemplo$\PageIndex{3}$

Para a função$f(x)=\sqrt[4]{5 x-4}$, encontre

$f(4)$
$f(-12)$

Solução:

uma.

$f(x)=\sqrt[4]{5 x-4}$

Para avaliar$f(4)$, substitua$4$ por$x$.

$f(4)=\sqrt[4]{5 \cdot 4-4}$

Simplifique.

$f(4)=\sqrt[4]{16}$

Pegue a quarta raiz.

$f(4)=2$

$f(x)=\sqrt[4]{5 x-4}$

Para avaliar$f(-12)$, substitua$-12$ por$x$.

$f(-12)=\sqrt[4]{5(-12)-4}$

Simplifique.

$f(-12)=\sqrt[4]{-64}$

Como a quarta raiz de um número negativo não é um número real, a função não tem um valor em$x=-12$.

Exercício$\PageIndex{5}$

Para a função$f(x)=\sqrt[4]{3 x+4}$, encontre

$f(4)$
$f(-1)$

Resposta

$f(4)=2$
$f(-1)=1$

Exercício$\PageIndex{6}$

Para a função$g(x)=\sqrt[4]{5 x+1}$, encontre

$g(16)$
$g(3)$

Resposta

$g(16)=3$
$g(3)=2$

Encontre o domínio de uma função radical

Para encontrar o domínio e a gama de funções radicais, usamos nossas propriedades dos radicais. Para um radical com um índice par, dissemos que o radicando tinha que ser maior ou igual a zero, pois as raízes pares de números negativos não são números reais. Para um índice ímpar, o radicando pode ser qualquer número real. Reafirmamos as propriedades aqui para referência.

Propriedades de$\sqrt[n]{a}$

Quando$n$ é um número par e:

$a \geq 0$, então$\sqrt[n]{a}$ é um número real.
$a<0$, então não$\sqrt[n]{a}$ é um número real.

Quando$n$ é um número ímpar,$\sqrt[n]{a}$ é um número real para todos os valores de$a$.

Então, para encontrar o domínio de uma função radical com índice par, definimos o radicando como maior ou igual a zero. Para um radical de índice ímpar, o radicando pode ser qualquer número real.

Domínio de uma função radical

Quando o índice do radical é par, o radicando deve ser maior ou igual a zero.

Quando o índice do radical é ímpar, o radicando pode ser qualquer número real.

Exemplo$\PageIndex{4}$

Encontre o domínio da função,$f(x)=\sqrt{3 x-4}$. Escreva o domínio em notação de intervalo.

Solução:

Como a função$f(x)=\sqrt{3 x-4}$ tem um radical com um índice de$2$, que é par, sabemos que o radicando deve ser maior ou igual$0$ a. Definimos o radicando como maior ou igual a$0$ e, em seguida, resolvemos encontrar o domínio.

Resolver.

$\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}$

O domínio de$f(x)=\sqrt{3 x-4}$ é todos os valores$x \geq \frac{4}{3}$ e nós o escrevemos em notação de intervalo como$\left[\frac{4}{3}, \infty\right)$.

Exercício$\PageIndex{7}$

Encontre o domínio da função,$f(x)=\sqrt{6 x-5}$. Escreva o domínio em notação de intervalo.

Resposta: $\left[\frac{5}{6}, \infty\right)$

Exercício$\PageIndex{8}$

Encontre o domínio da função,$f(x)=\sqrt{4-5 x}$. Escreva o domínio em notação de intervalo.

Resposta: $\left(-\infty, \frac{4}{5}\right]$

Exemplo$\PageIndex{5}$

Encontre o domínio da função,$g(x)=\sqrt{\frac{6}{x-1}}$. Escreva o domínio em notação de intervalo.

Solução:

Resolva a função,$g(x)=\sqrt{\frac{6}{x-1}}$ tem um radical com um índice de$2$, que é par, sabemos que o radicando deve ser maior ou igual$0$ a.

O radicando não pode ser zero, pois o numerador não é zero.

$\frac{6}{x-1}$Para ser maior que zero, o denominador deve ser positivo, pois o numerador é positivo. Sabemos que um positivo dividido por um positivo é positivo.

Nós definimos$x-1>0$ e resolvemos.

$x-1>0$

Resolver.

$x>1$

Além disso, como o radicando é uma fração, devemos perceber que o denominador não pode ser zero.

Resolvemos$x-1=0$ encontrar o valor que deve ser eliminado do domínio.

$x-1=0$

Resolver.

$x=1$então$x/neq 1$ no domínio.

Juntando isso, obtemos o domínio$x>1$ e o escrevemos como$(1, \infty)$.

Exercício$\PageIndex{9}$

Encontre o domínio da função,$f(x)=\sqrt{\frac{4}{x+3}}$. Escreva o domínio em notação de intervalo.

Resposta: $(-3, \infty)$

Exercício$\PageIndex{10}$

Encontre o domínio da função,$h(x)=\sqrt{\frac{9}{x-5}}$. Escreva o domínio em notação de intervalo.

Resposta: $(5, \infty)$

O próximo exemplo envolve uma raiz cúbica e, portanto, exigirá um pensamento diferente.

Exemplo$\PageIndex{6}$

Encontre o domínio da função,$f(x)=\sqrt[3]{2 x^{2}+3}$. Escreva o domínio em notação de intervalo.

Solução:

Como a função$f(x)=\sqrt[3]{2 x^{2}+3}$ tem um radical com um índice de$3$, o que é ímpar, sabemos que o radicando pode ser qualquer número real. Isso nos diz que o domínio é qualquer número real. Na notação de intervalo, escrevemos$(-\infty, \infty)$.

O domínio de$f(x)=\sqrt[3]{2 x^{2}+3}$ é todo números reais e nós o escrevemos em notação de intervalo como$(-\infty, \infty)$.

Exercício$\PageIndex{11}$

Encontre o domínio da função,$f(x)=\sqrt[3]{3 x^{2}-1}$. Escreva o domínio em notação de intervalo.

Resposta: $(-\infty, \infty)$

Exercício$\PageIndex{12}$

Encontre o domínio da função,$g(x)=\sqrt[3]{5 x-4}$. Escreva o domínio em notação de intervalo.

Resposta: $(-\infty, \infty)$

Funções radicais gráficas

Antes de representarmos graficamente qualquer função radical, primeiro encontramos o domínio da função. Para a função$f(x)=\sqrt{x}$, o índice é par e, portanto, o radicando deve ser maior ou igual$0$ a.

Isso nos diz que o domínio é$x≥0$ e escrevemos isso em notação de intervalo como$[0,∞)$.

Anteriormente, usávamos a plotagem de pontos para representar graficamente a função,$f(x)=\sqrt{x}$. Escolhemos$x$ -valores, os substituímos e, em seguida, criamos um gráfico. Observe que escolhemos pontos que são quadrados perfeitos para facilitar a obtenção da raiz quadrada.

A figura mostra o gráfico da função raiz quadrada no plano da coordenada x y. O eixo x do plano vai de 0 a 7. O eixo y vai de 0 a 7. A função tem um ponto de partida em (0, 0) e passa pelos pontos (1, 1) e (4, 2). Uma tabela é mostrada ao lado do gráfico com 3 colunas e 5 linhas. A primeira linha é uma linha de cabeçalho com as expressões â€œxâ€, â€œf (x) = raiz quadrada de xâ€ e â€ (x, f (x)) â€. A segunda linha tem os números 0, 0 e (0, 0). A terceira linha tem os números 1, 1 e (1, 1). A quarta linha tem os números 4, 2 e (4, 2). A quinta linha tem os números 9, 3 e (9, 3). — Figura 8.7.1

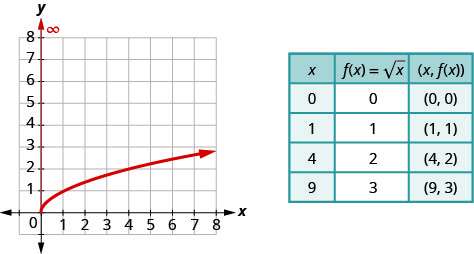
Depois de vermos o gráfico, podemos encontrar o alcance da função. $y$Os valores -da função são maiores ou iguais a zero. O alcance, então, é$[0,∞)$.

Exemplo$\PageIndex{7}$

Para a função$f(x)=\sqrt{x+3}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Solução:

Como o radical tem índice$2$, sabemos que o radicando deve ser maior ou igual a zero. Se$x+3 \geq 0$, então$x \geq-3$. Isso nos diz que o domínio tem todos os valores$x \geq-3$ e está escrito em notação de intervalo como$[-3, \infty)$.
Para representar graficamente a função, escolhemos pontos no intervalo$[-3, \infty)$ que também nos darão um radicando que será fácil de obter a raiz quadrada.

A figura mostra um gráfico da função de raiz quadrada no plano da coordenada x y. O eixo x do plano vai de menos 3 a 3. O eixo y vai de 0 a 7. A função tem um ponto de partida em (menos 3, 0) e passa pelos pontos (menos 2, 1) e (1, 2). Uma tabela é mostrada ao lado do gráfico com 3 colunas e 5 linhas. A primeira linha é uma linha de cabeçalho com as expressões â€œxâ€, â€œf (x) = raiz quadrada da quantidade x mais 3â€ e â€ (x, f (x)) â€. A segunda linha tem os números negativos 3, 0 e (menos 3, 0). A terceira linha tem os números negativos 2, 1 e (menos 2, 1). A quarta linha tem os números 1, 2 e (1, 2). A quinta linha tem os números 6, 3 e (6, 3). — Figura 8.7.2

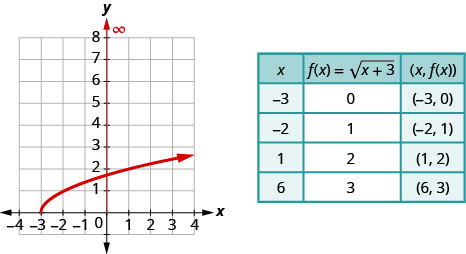
c. Olhando para o gráfico, vemos que$y$ os valores -da função são maiores ou iguais a zero. O alcance, então, é$[0, \infty)$.

Exercício$\PageIndex{13}$

Para a função$f(x)=\sqrt{x+2}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Resposta

domínio:$[-2, \infty)$
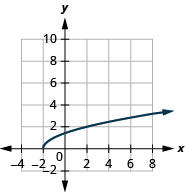
$A figura mostra um gráfico da função de raiz quadrada no plano da coordenada x y. O eixo x do plano vai de menos 2 a 6. O eixo y vai de 0 a 8. A função tem um ponto de partida em (menos 2, 0) e passa pelos pontos (menos 1, 1) e (2, 2).$
Figura 8.7.3
alcance:$[0, \infty)$

Exercício$\PageIndex{14}$

Para a função$f(x)=\sqrt{x-2}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Resposta

domínio:$[2, \infty)$
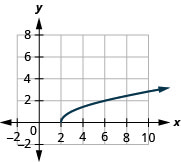
$A figura mostra um gráfico da função de raiz quadrada no plano da coordenada x y. O eixo x do plano vai de 0 a 8. O eixo y vai de 0 a 6. A função tem um ponto de partida em (2, 0) e passa pelos pontos (3, 1) e (6, 2).$
Figura 8.7.4
alcance:$[0, \infty)$

Em nosso trabalho anterior, representando graficamente funções, graficamos,$f(x)=x^{3}$ mas não representamos graficamente a função$f(x)=\sqrt[3]{x}$. Faremos isso agora no próximo exemplo.

Exemplo$\PageIndex{8}$

Para a função$f(x)=\sqrt[3]{x}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Solução:

a. Como o radical tem índice$3$, sabemos que o radicando pode ser qualquer número real. Isso nos diz que o domínio é todo em números reais e escrito em notação de intervalo como$(-\infty, \infty)$

b. Para representar graficamente a função, escolhemos pontos no intervalo$(-\infty, \infty)$ que também nos darão um radicando que será fácil de obter a raiz cúbica.

A figura mostra o gráfico da função raiz cúbica no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A função tem um ponto central em (0, 0) e passa pelos pontos (1, 1), (menos 1, menos 1), (8, 2) e (menos 8, menos 2). Uma tabela é mostrada ao lado do gráfico com 3 colunas e 6 linhas. A primeira linha é uma linha de cabeçalho com as expressões â€œxâ€, â€œf (x) = raiz cúbica de xâ€ e â€ (x, f (x)) â€. A segunda linha tem os números menos 8, menos 2 e (menos 8, menos 2). A terceira linha tem os números menos 1, menos 1 e (menos 1, menos 1). A quarta linha tem os números 0, 0 e (0, 0). A quinta linha tem os números 1, 1 e (1, 1). A sexta linha tem os números 8, 2 e (8, 2). — Figura 8.7.5

c. Olhando para o gráfico, vemos que$y$ os valores -da função são todos números reais. O alcance, então, é$(-\infty, \infty)$.

Exercício$\PageIndex{15}$

Para a função$f(x)=-\sqrt[3]{x}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Resposta

domínio:$(-\infty, \infty)$
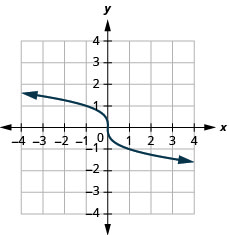
$A figura mostra um gráfico da função raiz cúbica no plano da coordenada x y. O eixo x do plano vai de menos 2 a 2. O eixo y vai de menos 2 a 2. A função tem um ponto central em (0, 0) e passa pelos pontos (1, menos 1) e (menos 1, 1).$
Figura 8.7.6
alcance:$(-\infty, \infty)$

Exercício$\PageIndex{16}$

Para a função$f(x)=\sqrt[3]{x-2}$,

encontre o domínio
representar graficamente a função
use o gráfico para determinar o intervalo

Resposta

domínio:$(-\infty, \infty)$
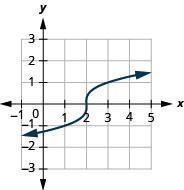
$A figura mostra um gráfico da função raiz cúbica no plano da coordenada x y. O eixo x do plano vai de menos 1 a 5. O eixo y vai de menos 3 a 3. A função tem um ponto central em (2, 0) e passa pelos pontos (1, menos 1) e (3, 2).$
Figura 8.7.7
alcance:$(-\infty, \infty)$

Acesse esses recursos on-line para obter instruções e práticas adicionais com funções radicais.

Domínio de uma função radical
Domínio de uma função radical 2
Encontrando o domínio de uma função radical

Conceitos chave

Propriedades de$\sqrt[n]{a}$
- Quando$n$ é um número par e:
  $a≥0$, então$\sqrt[n]{a}$ é um número real.
  $a<0$, então não$\sqrt[n]{a}$ é um número real.
- Quando$n$ é um número ímpar,$\sqrt[n]{a}$ é um número real para todos os valores de$a$.
Domínio de uma função radical
- Quando o índice do radical é par, o radicando deve ser maior ou igual a zero.
- Quando o índice do radical é ímpar, o radicando pode ser qualquer número real.

Glossário

função radical: Uma função radical é uma função definida por uma expressão radical.

Definição\(\PageIndex{1}\): radical function

Exemplo\(\PageIndex{1}\)

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Exemplo\(\PageIndex{6}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Exemplo\(\PageIndex{7}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Objetivos de

Avalie uma função radical

Definição\(\PageIndex{1}\): radical function

Exemplo\(\PageIndex{1}\)

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Encontre o domínio de uma função radical

Propriedades de\(\sqrt[n]{a}\)

Domínio de uma função radical

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Exemplo\(\PageIndex{6}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Funções radicais gráficas

Exemplo\(\PageIndex{7}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Conceitos chave

Glossário