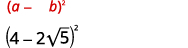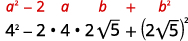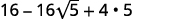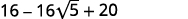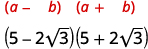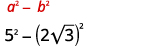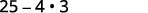Skip to main content
Global

8.5: Adicionar, subtrair e multiplicar expressões radicais

  1. Last updated
  2. Save as PDF
  • Page ID
    183472

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Adicione e subtraia expressões radicais
    • Multiplique expressões radicais
    • Use a multiplicação polinomial para multiplicar expressões radicais

    Antes de começar, faça este teste de prontidão.

    1. Adicionar:\(3x^{2}+9x−5−(x^{2}−2x+3)\).
      Se você perdeu esse problema, revise o Exemplo 5.5.
    2. Simplifique:\((2+a)(4−a)\).
      Se você perdeu esse problema, consulte o Exemplo 5.28.
    3. Simplifique:\((9−5y)^{2}\).
      Se você perdeu esse problema, consulte o Exemplo 5.31.

    Adicionar e subtrair expressões radicais

    Adicionar expressões radicais com o mesmo índice e o mesmo radicando é como adicionar termos semelhantes. Chamamos radicais com o mesmo índice e o mesmo radicando como radicais para nos lembrar de que eles funcionam da mesma forma que termos semelhantes.

    Definição\(\PageIndex{1}\): Like Radicals

    Radicais semelhantes são expressões radicais com o mesmo índice e o mesmo radicando.

    Somamos e subtraímos radicais semelhantes da mesma forma que adicionamos e subtraímos termos semelhantes. Sabemos que\(3x+8x\) é\(11x\). Da mesma forma, adicionamos\(3 \sqrt{x}+8 \sqrt{x}\) e o resultado é\(11 \sqrt{x}\).

    Pense em adicionar termos semelhantes com variáveis conforme você faz nos próximos exemplos. Quando você tem radicais semelhantes, basta somar ou subtrair os coeficientes. Quando os radicais não são iguais, você não pode combinar os termos.

    Exemplo\(\PageIndex{1}\)

    Simplifique:

    1. \(2 \sqrt{2}-7 \sqrt{2}\)
    2. \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)
    3. \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Solução:

    uma.

    \(2 \sqrt{2}-7 \sqrt{2}\)

    Como os radicais são semelhantes, subtraímos os coeficientes.

    \(-5 \sqrt{2}\)

    b.

    \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)

    Como os radicais são semelhantes, adicionamos os coeficientes.

    \(9 \sqrt[3]{y}\)

    c.

    \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Os índices são os mesmos, mas os radicais são diferentes. Eles não são como os radicais. Como os radicais não são parecidos, não podemos subtraí-los.

    Exercício\(\PageIndex{1}\)

    Simplifique:

    1. \(8 \sqrt{2}-9 \sqrt{2}\)
    2. \(4 \sqrt[3]{x}+7 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Resposta
    1. \(-\sqrt{2}\)
    2. \(11 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Exercício\(\PageIndex{2}\)

    Simplifique:

    1. \(5 \sqrt{3}-9 \sqrt{3}\)
    2. \(5 \sqrt[3]{y}+3 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)
    Resposta
    1. \(-4 \sqrt{3}\)
    2. \(8 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)

    Para que os radicais sejam semelhantes, eles devem ter o mesmo índice e radicando. Quando os radicandos contêm mais de uma variável, desde que todas as variáveis e seus expoentes sejam idênticos, os radicandos são os mesmos.

    Exemplo\(\PageIndex{2}\)

    Simplifique:

    1. \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)
    2. \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Solução:

    uma.

    \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)

    Como os radicais são semelhantes, nós os combinamos.

    \(0 \sqrt{5 n}\)

    Simplifique.

    \(0\)

    b.

    \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Como os radicais são semelhantes, nós os combinamos.

    \(2 \sqrt[4]{3 x y}\)

    Exercício\(\PageIndex{3}\)

    Simplifique:

    1. \(\sqrt{7 x}-7 \sqrt{7 x}+4 \sqrt{7 x}\)
    2. \(4 \sqrt[4]{5 x y}+2 \sqrt[4]{5 x y}-7 \sqrt[4]{5 x y}\)
    Resposta
    1. \(-2 \sqrt{7 x}\)
    2. \(-\sqrt[4]{5 x y}\)
    Exercício\(\PageIndex{4}\)

    Simplifique:

    1. \(4 \sqrt{3 y}-7 \sqrt{3 y}+2 \sqrt{3 y}\)
    2. \(6 \sqrt[3]{7 m n}+\sqrt[3]{7 m n}-4 \sqrt[3]{7 m n}\)
    Resposta
    1. \(-\sqrt{3 y}\)
    2. \(3 \sqrt[3]{7 m n}\)

    Lembre-se de que sempre simplificamos os radicais removendo o maior fator do radicando, que é a potência do índice. Uma vez que cada radical é simplificado, podemos então decidir se eles são como os radicais.

    Exemplo\(\PageIndex{3}\)

    Simplifique:

    1. \(\sqrt{20}+3 \sqrt{5}\)
    2. \(\sqrt[3]{24}-\sqrt[3]{375}\)
    3. \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Solução:

    uma.

    \(\sqrt{20}+3 \sqrt{5}\)

    Simplifique os radicais, quando possível.

    \(\sqrt{4} \cdot \sqrt{5}+3 \sqrt{5}\)

    \(2 \sqrt{5}+3 \sqrt{5}\)

    Combine os radicais semelhantes.

    \(5 \sqrt{5}\)

    b.

    \(\sqrt[3]{24}-\sqrt[3]{375}\)

    Simplifique os radicais.

    \(\sqrt[3]{8} \cdot \sqrt[3]{3}-\sqrt[3]{125} \cdot \sqrt[3]{3}\)

    \(2 \sqrt[3]{3}-5 \sqrt[3]{3}\)

    Combine os radicais semelhantes.

    \(-3 \sqrt[3]{3}\)

    c.

    \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Simplifique os radicais.

    \(\frac{1}{2} \sqrt[4]{16} \cdot \sqrt[4]{3}-\frac{2}{3} \sqrt[4]{81} \cdot \sqrt[4]{3}\)

    \(\frac{1}{2} \cdot 2 \cdot \sqrt[4]{3}-\frac{2}{3} \cdot 3 \cdot \sqrt[4]{3}\)

    \(\sqrt[4]{3}-2 \sqrt[4]{3}\)

    Combine os radicais semelhantes.

    \(-\sqrt[4]{3}\)

    Exercício\(\PageIndex{5}\)

    Simplifique:

    1. \(\sqrt{18}+6 \sqrt{2}\)
    2. \(6 \sqrt[3]{16}-2 \sqrt[3]{250}\)
    3. \(\frac{2}{3} \sqrt[3]{81}-\frac{1}{2} \sqrt[3]{24}\)
    Resposta
    1. \(9 \sqrt{2}\)
    2. \(2 \sqrt[3]{2}\)
    3. \(\sqrt[3]{3}\)
    Exercício\(\PageIndex{6}\)

    Simplifique:

    1. \(\sqrt{27}+4 \sqrt{3}\)
    2. \(4 \sqrt[3]{5}-7 \sqrt[3]{40}\)
    3. \(\frac{1}{2} \sqrt[3]{128}-\frac{5}{3} \sqrt[3]{54}\)
    Resposta
    1. \(7 \sqrt{3}\)
    2. \(-10 \sqrt[3]{5}\)
    3. \(-3 \sqrt[3]{2}\)

    No próximo exemplo, removeremos fatores constantes e variáveis dos radicais. Agora que praticamos pegar as raízes pares e ímpares das variáveis, é prática comum, neste momento, supor que todas as variáveis são maiores ou iguais a zero para que valores absolutos não sejam necessários. Usaremos essa suposição ao longo do restante deste capítulo.

    Exemplo\(\PageIndex{4}\)

    Simplifique:

    1. \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)
    2. \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Solução:

    uma.

    \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)

    Simplifique os radicais.

    \(9 \sqrt{25 m^{2}} \cdot \sqrt{2}-6 \sqrt{16 m^{2}} \cdot \sqrt{3}\)

    \(9 \cdot 5 m \cdot \sqrt{2}-6 \cdot 4 m \cdot \sqrt{3}\)

    \(45 m \sqrt{2}-24 m \sqrt{3}\)

    Os radicais não são semelhantes e, portanto, não podem ser combinados.

    b.

    \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Simplifique os radicais.

    \(\sqrt[3]{27 n^{3}} \cdot \sqrt[3]{2 n^{2}}-\sqrt[3]{8 n^{3}} \cdot \sqrt[3]{2 n^{2}}\)

    \(3 n \sqrt[3]{2 n^{2}}-2 n \sqrt[3]{2 n^{2}}\)

    Combine os radicais semelhantes.

    \(n \sqrt[3]{2 n^{2}}\)

    Exercício\(\PageIndex{7}\)

    Simplifique:

    1. \(\sqrt{32 m^{7}}-\sqrt{50 m^{7}}\)
    2. \(\sqrt[3]{135 x^{7}}-\sqrt[3]{40 x^{7}}\)
    Resposta
    1. \(-m^{3} \sqrt{2 m}\)
    2. \(x^{2} \sqrt[3]{5 x}\)
    Exercício\(\PageIndex{8}\)

    Simplifique:

    1. \(\sqrt{27 p^{3}}-\sqrt{48 p^{3}}\)
    2. \(\sqrt[3]{256 y^{5}}-\sqrt[3]{32 n^{5}}\)
    Resposta
    1. \(-p \sqrt{3 p}\)
    2. \(4 y \sqrt[3]{4 y^{2}}-2 n \sqrt[3]{4 n^{2}}\)

    Multiplique expressões radicais

    Usamos a propriedade de produto das raízes para simplificar as raízes quadradas, removendo os fatores quadrados perfeitos. Podemos usar a propriedade de produto das raízes “ao contrário” para multiplicar as raízes quadradas. Lembre-se de que assumimos que todas as variáveis são maiores ou iguais a zero.

    Vamos reescrever a propriedade de produto das raízes para que possamos ver os dois lados juntos.

    Definição\(\PageIndex{2}\): Product Property of Roots

    Para qualquer número real\(\sqrt[n]{a}\) e\(\sqrt[b]{n}\), e para qualquer número inteiro\(n≥2\)

    \(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad \text { and } \quad \sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)

    Quando multiplicamos dois radicais, eles devem ter o mesmo índice. Depois de multiplicarmos os radicais, procuramos fatores que sejam uma potência do índice e simplificamos o radical sempre que possível.

    Multiplicar radicais por coeficientes é muito parecido com multiplicar variáveis por coeficientes. Para multiplicar,\(4x⋅3y\) multiplicamos os coeficientes juntos e depois as variáveis. O resultado é\(12xy\). Lembre-se disso ao fazer esses exemplos.

    Exemplo\(\PageIndex{5}\)

    Simplifique:

    1. \((6 \sqrt{2})(3 \sqrt{10})\)
    2. \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Solução:

    uma.

    \((6 \sqrt{2})(3 \sqrt{10})\)

    Multiplique usando a propriedade do produto.

    \(18\sqrt{20}\)

    Simplifique o radical.

    \(18 \sqrt{4} \cdot \sqrt{5}\)

    Simplifique.

    \(18 \cdot 2 \cdot \sqrt{5}\)

    \(36 \sqrt{5}\)

    b.

    \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Multiplique usando a propriedade do produto.

    \(20 \sqrt[3]{24}\)

    Simplifique o radical.

    \(20 \sqrt[3]{8} \cdot \sqrt[3]{3}\)

    Simplifique.

    \(20 \cdot 2 \cdot \sqrt[3]{3}\)

    \(40 \sqrt[3]{3}\)

    Exercício\(\PageIndex{9}\)

    Simplifique:

    1. \((3 \sqrt{2})(2 \sqrt{30})\)
    2. \((2 \sqrt[3]{18})(-3 \sqrt[3]{6})\)
    Resposta
    1. \(12 \sqrt{15}\)
    2. \(-18 \sqrt[3]{2}\)
    Exercício\(\PageIndex{10}\)

    Simplifique:

    1. \((3 \sqrt{3})(3 \sqrt{6})\)
    2. \((-4 \sqrt[3]{9})(3 \sqrt[3]{6})\)
    Resposta
    1. \(27 \sqrt{2}\)
    2. \(-36 \sqrt[3]{2}\)

    Seguimos os mesmos procedimentos quando há variáveis nos radicandos.

    Exemplo\(\PageIndex{6}\)

    Simplifique:

    1. \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)
    2. \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Solução:

    uma.

    \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)

    Multiplique.

    \(40 \sqrt{18 p^{4}}\)

    Simplifique o radical.

    \(40 \sqrt{9 p^{4}} \cdot \sqrt{2}\)

    Simplifique.

    \(40 \cdot 3 p^{2} \cdot \sqrt{3}\)

    \(120 p^{2} \sqrt{3}\)

    b. Quando os radicandos envolvem grandes números, muitas vezes é vantajoso fatorá-los para encontrar os poderes perfeitos.

    \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Multiplique.

    \(6 \sqrt[4]{4 \cdot 5 \cdot 4 \cdot 7 y^{5}}\)

    Simplifique o radical.

    \(6 \sqrt[4]{16 y^{4}} \cdot \sqrt[4]{35 y}\)

    Simplifique.

    \(6 \cdot 2 y \sqrt[4]{35 y}\)

    Multiplique.

    \(12 y \sqrt[4]{35 y}\)

    Exercício\(\PageIndex{11}\)

    Simplifique:

    1. \(\left(6 \sqrt{6 x^{2}}\right)\left(8 \sqrt{30 x^{4}}\right)\)
    2. \(\left(-4 \sqrt[4]{12 y^{3}}\right)\left(-\sqrt[4]{8 y^{3}}\right)\)
    Resposta
    1. \(36 x^{3} \sqrt{5}\)
    2. \(8 y \sqrt[4]{3 y^{2}}\)
    Exercício\(\PageIndex{12}\)

    Simplifique:

    1. \(\left(2 \sqrt{6 y^{4}}\right)(12 \sqrt{30 y})\)
    2. \(\left(-4 \sqrt[4]{9 a^{3}}\right)\left(3 \sqrt[4]{27 a^{2}}\right)\)
    Resposta
    1. \(144 y^{2} \sqrt{5 y}\)
    2. \(-36 \sqrt[4]{3 a}\)

    Use a multiplicação polinomial para multiplicar expressões radicais

    Nos próximos exemplos, usaremos a Propriedade Distributiva para multiplicar expressões por radicais. Primeiro, distribuiremos e depois simplificaremos os radicais quando possível.

    Exemplo\(\PageIndex{7}\)

    Simplifique:

    1. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)
    2. \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Solução:

    uma.

    \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)

    Multiplique.

    \(\sqrt{12}+\sqrt{108}\)

    Simplifique.

    \(\sqrt{4} \cdot \sqrt{3}+\sqrt{36} \cdot \sqrt{3}\)

    Simplifique.

    \(2 \sqrt{3}+6 \sqrt{3}\)

    Combine como radicais.

    \(8\sqrt{3}\)

    b.

    \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Distribuir.

    \(5 \sqrt[3]{9}-\sqrt[3]{162}\)

    Simplifique.

    \(5 \sqrt[3]{9}-\sqrt[3]{27} \cdot \sqrt[3]{6}\)

    Simplifique.

    \(5 \sqrt[3]{9}-3 \sqrt[3]{6}\)

    Exercício\(\PageIndex{13}\)

    Simplifique:

    1. \(\sqrt{6}(1+3 \sqrt{6})\)
    2. \(\sqrt[3]{4}(-2-\sqrt[3]{6})\)
    Resposta
    1. \(18+\sqrt{6}\)
    2. \(-2 \sqrt[3]{4}-2 \sqrt[3]{3}\)
    Exercício\(\PageIndex{14}\)

    Simplifique:

    1. \(\sqrt{8}(2-5 \sqrt{8})\)
    2. \(\sqrt[3]{3}(-\sqrt[3]{9}-\sqrt[3]{6})\)
    Resposta
    1. \(-40+4 \sqrt{2}\)
    2. \(-3-\sqrt[3]{18}\)

    Quando trabalhamos com polinômios, multiplicamos binômios por binômios. Lembre-se de que isso nos deu quatro produtos antes de combinarmos termos semelhantes. Para ter certeza de adquirir todos os quatro produtos, organizamos nosso trabalho, geralmente pelo método FOIL.

    Exemplo\(\PageIndex{8}\)

    Simplifique:

    1. \((3-2 \sqrt{7})(4-2 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Solução:

    uma.

    \((3-2 \sqrt{7})(4-2 \sqrt{7})\)

    Multiplique.

    \(12-6 \sqrt{7}-8 \sqrt{7}+4 \cdot 7\)

    Simplifique.

    \(12-6 \sqrt{7}-8 \sqrt{7}+28\)

    Combine termos semelhantes.

    \(40-14 \sqrt{7}\)

    b.

    \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Multiplique.

    \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}-2 \sqrt[3]{x}-8\)

    Combine termos semelhantes.

    \(\sqrt[3]{x^{2}}+2 \sqrt[3]{x}-8\)

    Exercício\(\PageIndex{15}\)

    Simplifique:

    1. \((6-3 \sqrt{7})(3+4 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}-3)\)
    Resposta
    1. \(-66+15 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-5 \sqrt[3]{x}+6\)
    Exercício\(\PageIndex{16}\)

    Simplifique:

    1. \((2-3 \sqrt{11})(4-\sqrt{11})\)
    2. \((\sqrt[3]{x}+1)(\sqrt[3]{x}+3)\)
    Resposta
    1. \(41-14 \sqrt{11}\)
    2. \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}+3\)
    Exemplo\(\PageIndex{9}\)

    Simplifique:\((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Solução:

    \((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Multiplique.

    \(3 \cdot 2+12 \sqrt{10}-\sqrt{10}-4 \cdot 5\)

    Simplifique.

    \(6+12 \sqrt{10}-\sqrt{10}-20\)

    Combine termos semelhantes.

    \(-14+11 \sqrt{10}\)

    Exercício\(\PageIndex{17}\)

    Simplifique:\((5 \sqrt{3}-\sqrt{7})(\sqrt{3}+2 \sqrt{7})\)

    Resposta

    \(1+9 \sqrt{21}\)

    Exercício\(\PageIndex{18}\)

    Simplifique:\((\sqrt{6}-3 \sqrt{8})(2 \sqrt{6}+\sqrt{8})\)

    Resposta

    \(-12-20 \sqrt{3}\)

    O reconhecimento de alguns produtos especiais facilitou nosso trabalho quando multiplicamos os binômios anteriormente. Isso também é verdade quando multiplicamos radicais. As fórmulas especiais de produtos que usamos são mostradas aqui.

    Produtos especiais

    Quadrados binomiais

    \(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Produto de conjugados

    \((a+b)(a-b)=a^{2}-b^{2}\)

    Usaremos as fórmulas de produtos especiais nos próximos exemplos. Começaremos com o Produto do Padrão de Quadrados Binomiais.

    Exemplo\(\PageIndex{10}\)

    Simplifique:

    1. \(2+\sqrt{3})^{2}\)
    2. \((4-2 \sqrt{5})^{2}\)

    Solução:

    uma.

      .
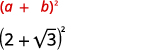    Multiplique usando o Produto do Padrão de Quadrados Binomiais. .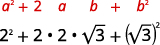
    Simplifique. .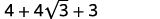
    Combine termos semelhantes. .
    Tabela 8.4.1

    b.

    Tabela 8.4.2
     

    .
    Múltiplo, usando o Produto do Padrão de Quadrados Binomiais.

    .
    Simplifique.

    .
     

    .
    Combine termos semelhantes.

    .
    Exercício\(\PageIndex{19}\)

    Simplifique:

    1. \((10+\sqrt{2})^{2}\)
    2. \((1+3 \sqrt{6})^{2}\)
    Resposta
    1. \(102+20 \sqrt{2}\)
    2. \(55+6 \sqrt{6}\)
    Exercício\(\PageIndex{20}\)

    Simplifique:

    1. \((6-\sqrt{5})^{2}\)
    2. \((9-2 \sqrt{10})^{2}\)
    Resposta
    1. \(41-12 \sqrt{5}\)
    2. \(121-36 \sqrt{10}\)

    No próximo exemplo, usaremos o Padrão Produto de Conjugados. Observe que o produto final não tem radicais.

    Exemplo\(\PageIndex{11}\)

    Simplifique:\((5-2 \sqrt{3})(5+2 \sqrt{3})\)

    Solução:

     

    .
    Multiplique usando o padrão Produto dos Conjugados.

    .
    Simplifique.

    .
     

    .
    Tabela 8.4.3
    Exercício\(\PageIndex{21}\)

    Simplifique:\((3-2 \sqrt{5})(3+2 \sqrt{5})\)

    Resposta

    \(-11\)

    Exercício\(\PageIndex{22}\)

    Simplifique:\((4+5 \sqrt{7})(4-5 \sqrt{7})\)

    Resposta

    \(-159\)

    Acesse esses recursos on-line para obter instruções e práticas adicionais com adição, subtração e multiplicação de expressões radicais.

    • Multiplicação da adição e subtração de radicais
    • Multiplicação de produtos especiais: binômios quadrados contendo raízes quadradas
    • Multiplicação de conjugados

    Conceitos-chave

    • Propriedade de produto das raízes
      • Para qualquer número real\(\sqrt[n]{a}\) e\(\sqrt[n]{b}\), e para qualquer número inteiro\(n≥2\)\(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b}\) e\(\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)
    • Produtos especiais

    \(\begin{array}{c c}{\text { Binomial Squares }}& {\text{Product of Conjugates}} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a+b)(a-b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Glossário

    como radicais
    Radicais semelhantes são expressões radicais com o mesmo índice e o mesmo radicando.