8.2: Simplifique expressões com raízes
- Page ID
- 183436
Ao final desta seção, você poderá:
- Simplifique expressões com raízes
- Estime e aproxime as raízes
- Simplifique expressões variáveis com raízes
Antes de começar, faça este teste de prontidão.
- Simplifique: a.\((−9)^{2}\) b.\(-9^{2}\) c.\((−9)^{3}\)
Se você perdeu esse problema, consulte o Exemplo 2.21. - Arredonde\(3.846\) para o centésimo mais próximo.
Se você perdeu esse problema, revise o Exemplo 1.34. - Simplifique: a.\(x^{3} \cdot x^{3}\) b.\(y^{2} \cdot y^{2} \cdot y^{2}\) c.\(z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}\)
Se você perdeu esse problema, consulte o Exemplo 5.12.
Simplifique expressões com raízes
Em Foundations, analisamos brevemente as raízes quadradas. Lembre-se de que quando um número real\(n\) é multiplicado por si mesmo, nós o escrevemos\(n^{2}\) e lemos “\(n^{2}\)ao quadrado”. Esse número é chamado de quadrado de\(n\) e\(n\) é chamado de raiz quadrada. Por exemplo,
\(13^{2}\)é lido “\(13\)ao quadrado”
\(169\)é chamado de quadrado de\(13\), já que\(13^{2}=169\)
\(13\)é uma raiz quadrada de\(169\)
Quadrado
Se\(n^{2}=m\), então\(m\) é o quadrado de\(n\).
raiz quadrada
Se\(n^{2}=m\), então\(n\) é uma raiz quadrada de\(m\).
Observe\((−13)^{2} = 169\) também, então também\(−13\) é uma raiz quadrada de\(169\). Portanto, ambos\(13\) e\(−13\) são raízes quadradas de\(169\).
Então, todo número positivo tem duas raízes quadradas — uma positiva e uma negativa. E se quiséssemos apenas a raiz quadrada positiva de um número positivo? Usamos um sinal radical e escrevemos,\(\sqrt{m}\), que denota a raiz quadrada positiva de\(m\). A raiz quadrada positiva também é chamada de raiz quadrada principal.
Também usamos o sinal radical para a raiz quadrada de zero. Porque\(0^{2}=0, \sqrt{0}=0\). Observe que zero tem apenas uma raiz quadrada.
\(\sqrt{m}\)é lido como “a raiz quadrada de”\(m\).
E se\(n^{2}=m\), então\(n=\sqrt{m}\), para\(n\geq 0\).
Sabemos que todo número positivo tem duas raízes quadradas e o sinal radical indica o positivo. Nós escrevemos\(\sqrt{169}=13\). Se quisermos encontrar a raiz quadrada negativa de um número, colocamos um negativo na frente do sinal radical. Por exemplo,\(-\sqrt{169}=-13\).
Simplifique:
- \(\sqrt{144}\)
- \(-\sqrt{289}\)
Solução:
uma.
\(\sqrt{144}\)
Desde\(12^{2}=144\).
\(12\)
b.
\(-\sqrt{289}\)
Desde\(17^{2}=289\) e o negativo estão na frente do signo radical.
\(-17\)
Simplifique:
- \(-\sqrt{64}\)
- \(\sqrt{225}\)
- Responda
-
- \(-8\)
- \(15\)
Simplifique:
- \(\sqrt{100}\)
- \(-\sqrt{121}\)
- Responda
-
- \(10\)
- \(-11\)
Podemos simplificar\(-\sqrt{49}\)? Existe um número cujo quadrado é\(-49\)?
\((\)___\( )^{2}=-49\)
Qualquer número positivo ao quadrado é positivo. Qualquer número negativo ao quadrado é positivo. Não há número real igual\(\sqrt{-49}\) a. A raiz quadrada de um número negativo não é um número real.
Simplifique:
- \(\sqrt{-196}\)
- \(-\sqrt{64}\)
Solução:
uma.
\(\sqrt{-196}\)
Não existe um número real cujo quadrado seja\(-196\).
\(\sqrt{-196}\)não é um número real.
b.
\(-\sqrt{64}\)
O negativo está na frente do radical.
\(-8\)
Simplifique:
- \(\sqrt{-169}\)
- \(-\sqrt{81}\)
- Responda
-
- não é um número real
- \(-9\)
Simplifique:
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- Responda
-
- \(-7\)
- não é um número real
Até agora, falamos apenas sobre quadrados e raízes quadradas. Vamos agora estender nosso trabalho para incluir poderes superiores e raízes superiores.
Vamos revisar um pouco do vocabulário primeiro.
\(\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}\)
Os termos “quadrado” e “cubo” vêm das fórmulas para a área de um quadrado e o volume de um cubo.
Será útil ter uma tabela das potências dos números inteiros de\(−5\) até\(5\). Veja a Figura 8.1.2
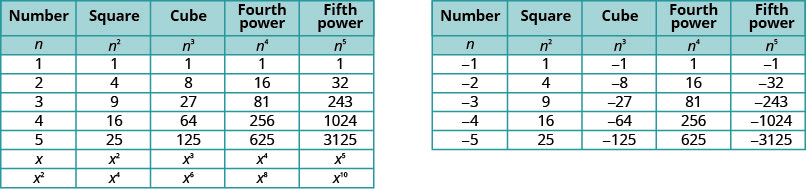
Observe os sinais na tabela. Todos os poderes dos números positivos são positivos, é claro. Mas quando temos um número negativo, as potências pares são positivas e as potências ímpares são negativas. Vamos copiar a linha com os poderes de\(−2\) para ajudar você a ver isso.
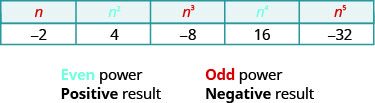
Agora estenderemos a definição de raiz quadrada para raízes mais altas.
Se\(b^{n}=a\), então\(b\) é uma\(n^{th}\) raiz de\(a\).
A\(n^{th}\) raiz principal do\(a\) está escrita\(\sqrt[n]{a}\).
O\(n\) é chamado de índice do radical.
Assim como usamos a palavra “cubo” para\(b^{3}\), usamos o termo “raiz cúbica” para\(\sqrt[3]{a}\).
Podemos consultar a Figura 8.1.2 para ajudar a encontrar raízes mais altas.
\(\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}\)
Poderíamos ter uma raiz par de um número negativo? Sabemos que a raiz quadrada de um número negativo não é um número real. O mesmo vale para qualquer raiz uniforme. Mesmo as raízes dos números negativos não são números reais. As raízes ímpares dos números negativos são números reais.
Propriedades de\(\sqrt[n]{a}\)
Quando\(n\) é um número par e
- \(a \geq 0\), então\(\sqrt[n]{a}\) é um número real.
- \(a<0\), então não\(\sqrt[n]{a}\) é um número real.
Quando\(n\) é um número ímpar,\(\sqrt[n]{a}\) é um número real para todos os valores de\(a\).
Aplicaremos essas propriedades nos próximos dois exemplos.
Simplifique:
- \(\sqrt[3]{64}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)
Solução:
uma.
\(\sqrt[3]{64}\)
Desde\(4^{3}=64\).
\(4\)
b.
\(\sqrt[4]{81}\)
Desde\((3)^{4}=81\).
\(3\)
c.
\(\sqrt[5]{32}\)
Desde\((2)^{5}=32\).
\(2\)
Simplifique:
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{243}\)
- Responda
-
- \(3\)
- \(4\)
- \(3\)
Simplifique:
- \(\sqrt[3]{1000}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{243}\)
- Responda
-
- \(10\)
- \(2\)
- \(3\)
Neste exemplo, fique atento aos sinais negativos, bem como às potências pares e ímpares.
Simplifique:
- \(\sqrt[3]{-125}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{-243}\)
Solução:
uma.
\(\sqrt[3]{-125}\)
Desde\((-5)^{3}=-125\).
\(-5\)
b.
\(\sqrt[4]{16}\)
Pense,\((?)^{4}=-16\). Nenhum número real elevado à quarta potência é negativo.
Não é um número real.
c.
\(\sqrt[5]{-243}\)
Desde\((-3)^{5}=-243\).
\(-3\)
Simplifique:
- \(\sqrt[3]{-27}\)
- \(\sqrt[4]{-256}\)
- \(\sqrt[5]{-32}\)
- Responda
-
- \(-3\)
- não é real
- \(-2\)
Simplifique:
- \(\sqrt[3]{-216}\)
- \(\sqrt[4]{-81}\)
- \(\sqrt[5]{-1024}\)
- Responda
-
- \(-6\)
- não é real
- \(-4\)
Estimativa e raízes aproximadas
Quando vemos um número com um sinal radical, muitas vezes não pensamos em seu valor numérico. Embora provavelmente saibamos que\(\sqrt{4}=2\), qual é o valor de\(\sqrt{21}\) ou\(\sqrt[3]{50}\)? Em algumas situações, uma estimativa rápida é significativa e, em outras, é conveniente ter uma aproximação decimal.
Para obter uma estimativa numérica de uma raiz quadrada, procuramos números quadrados perfeitos mais próximos do radicando. Para encontrar uma estimativa de\(\sqrt{11}\), vemos que\(11\) está entre números quadrados perfeitos\(9\) e\(16\), mais perto de\(9\). Sua raiz quadrada então estará entre\(3\) e\(4\), mas mais perto de\(3\).
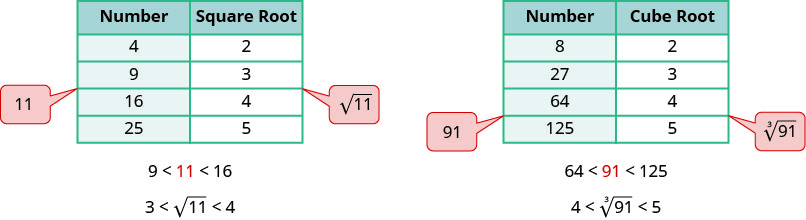
Da mesma forma, para estimar\(\sqrt[3]{91}\), vemos que\(91\) está entre números de cubos perfeitos\(64\)\(125\) e. A raiz cúbica então estará entre\(4\)\(5\) e.
Estime cada raiz entre dois números inteiros consecutivos:
- \(\sqrt{105}\)
- \(\sqrt[3]{43}\)
Solução:
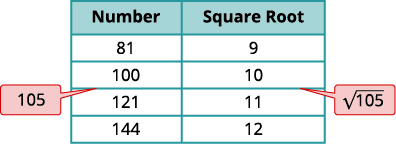
a. Pense nos números quadrados perfeitos mais próximos de\(105\). Faça uma pequena mesa com esses quadrados perfeitos e suas raízes quadradas.
| \(\sqrt{105}\) | |
 |
|
| Localize\(105\) entre dois quadrados perfeitos consecutivos. | \(100<\color{red}105 \color{black} <121\) |
| \(\sqrt{105}\)está entre suas raízes quadradas. | \(10< \color{red}\sqrt{105}< \color{black}11\) |
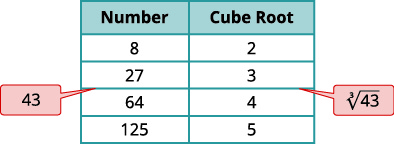
b. Da mesma forma, localizamos\(43\) entre dois números de cubos perfeitos.
| \(\sqrt[3]{43}\) | |
 |
|
| Localize\(43\) entre dois cubos perfeitos consecutivos. |  |
| \(\sqrt[3]{43}\)está entre suas raízes cúbicas. |  |
Estime cada raiz entre dois números inteiros consecutivos:
- \(\sqrt{38}\)
- \(\sqrt[3]{93}\)
- Responda
-
- \(6<\sqrt{38}<7\)
- \(4<\sqrt[3]{93}<5\)
Estime cada raiz entre dois números inteiros consecutivos:
- \(\sqrt{84}\)
- \(\sqrt[3]{152}\)
- Responda
-
- \(9<\sqrt{84}<10\)
- \(5<\sqrt[3]{152}<6\)
Existem métodos matemáticos para aproximar raízes quadradas, mas hoje em dia a maioria das pessoas usa uma calculadora para encontrar raízes quadradas. Para encontrar uma raiz quadrada, você usará a\(\sqrt{x}\) chave na sua calculadora. Para encontrar uma raiz cúbica ou qualquer raiz com maior índice, você usará a\(\sqrt[y]{x}\) chave.
Ao usar essas teclas, você obtém um valor aproximado. É uma aproximação, precisa do número de dígitos mostrados na tela da sua calculadora. O símbolo para uma aproximação é\(≈\) e é lido 'aproximadamente'.
Suponha que sua calculadora tenha uma exibição de\(10\) dígitos. Você veria isso
\(\sqrt{5} \approx 2.236067978\)arredondado para duas casas decimais é\(\sqrt{5} \approx 2.24\)
\(\sqrt[4]{93} \approx 3.105422799\)arredondado para duas casas decimais é\(\sqrt[4]{93} \approx 3.11\)
Como sabemos que esses valores são aproximações e não valores exatos? Veja o que acontece quando os quadramos:
\(\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}\)
Seus quadrados estão próximos\(5\), mas não são exatamente iguais\(5\) a. As quartas potências estão próximas\(93\), mas não são iguais\(93\).
Arredonde para duas casas decimais:
- \(\sqrt{17}\)
- \(\sqrt[3]{49}\)
- \(\sqrt[4]{51}\)
Solução:
uma.
\(\sqrt{17}\)
Use a chave de raiz quadrada da calculadora.
\(4.123105626 \dots\)
Arredonde para duas casas decimais.
\(4.12\)
\(\sqrt{17} \approx 4.12\)
b.
\(\sqrt[3]{49}\)
Use a\(\sqrt[y]{x}\) tecla da calculadora.
\(3.659305710 \ldots\)
Arredonde para duas casas decimais.
\(3.66\)
\(\sqrt[3]{49} \approx 3.66\)
c.
\(\sqrt[4]{51}\)
Use a\(\sqrt[y]{x}\) tecla da calculadora.
\(2.6723451177 \ldots\)
Arredonde para duas casas decimais.
\(2.67\)
\(\sqrt[4]{51} \approx 2.67\)
Arredonde para duas casas decimais:
- \(\sqrt{11}\)
- \(\sqrt[3]{71}\)
- \(\sqrt[4]{127}\)
- Responda
-
- \(\approx 3.32\)
- \(\approx 4.14\)
- \(\approx 3.36\)
Arredonde para duas casas decimais:
- \(\sqrt{13}\)
- \(\sqrt[3]{84}\)
- \(\sqrt[4]{98}\)
- Responda
-
- \(\approx 3.61\)
- \(\approx 4.38\)
- \(\approx 3.15\)
Simplifique expressões variáveis com raízes
A raiz ímpar de um número pode ser positiva ou negativa. Por exemplo,
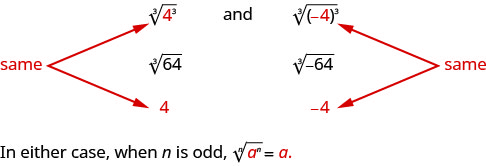
Mas que tal uma raiz uniforme? Queremos a raiz principal, então\(\sqrt[4]{625}=5\).
Mas observe,
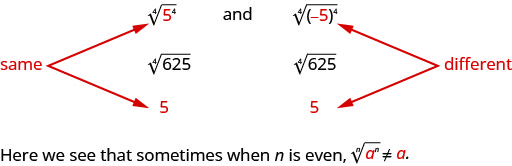
Como podemos garantir que a quarta raiz de\(−5\) elevada à quarta potência seja\(5\)? Podemos usar o valor absoluto. \(|−5|=5\). Então, dizemos que quando\(n\) é par\(\sqrt[n]{a^{n}}=|a|\). Isso garante que a raiz principal seja positiva.
Para qualquer número inteiro\(n\geq 2\),
quando o índice\(n\) é ímpar\(\sqrt[n]{a^{n}}=a\)
quando o índice\(n\) é uniforme\(\sqrt[n]{a^{n}}=|a|\)
Devemos usar os sinais de valor absoluto quando tomamos uma raiz uniforme de uma expressão com uma variável no radical.
Simplifique:
- \(\sqrt{x^{2}}\)
- \(\sqrt[3]{n^{3}}\)
- \(\sqrt[4]{p^{4}}\)
- \(\sqrt[5]{y^{5}}\)
Solução:
a. Usamos o valor absoluto para ter certeza de obter a raiz positiva.
\(\sqrt{x^{2}}\)
Como o índice\(n\) é uniforme,\(\sqrt[n]{a^{n}}=|a|\).
b. Essa é uma raiz indexada ímpar, então não há necessidade de um sinal de valor absoluto.
\(\sqrt[3]{m^{3}}\)
Como o índice\(n\) é ímpar,\(\sqrt[n]{a^{n}}=a\).
\(m\)
c.
\(\sqrt[4]{p^{4}}\)
Já que o índice\(n\) é uniforme\(\sqrt[n]{a^{n}}=|a|\).
\(|p|\)
d.
\(\sqrt[5]{y^{5}}\)
Como o índice\(n\) é ímpar,\(\sqrt[n]{a^{n}}=a\).
\(y\)
Simplifique:
- \(\sqrt{b^{2}}\)
- \(\sqrt[3]{w^{3}}\)
- \(\sqrt[4]{m^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Responda
-
- \(|b|\)
- \(w\)
- \(|m|\)
- \(q\)
Simplifique:
- \(\sqrt{y^{2}}\)
- \(\sqrt[3]{p^{3}}\)
- \(\sqrt[4]{z^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Responda
-
- \(|y|\)
- \(p\)
- \(|z|\)
- \(q\)
E quanto às raízes quadradas das maiores potências das variáveis? A propriedade de poder dos expoentes diz\(\left(a^{m}\right)^{n}=a^{m \cdot n}\). Então, se fizermos o quadrado\(a^{m}\), o expoente se tornará\(2m\).
\(\left(a^{m}\right)^{2}=a^{2 m}\)
Olhando agora para a raiz quadrada.
\(\sqrt{a^{2 m}}\)
Desde\(\left(a^{m}\right)^{2}=a^{2 m}\).
\(\sqrt{\left(a^{m}\right)^{2}}\)
Desde que\(n\) está empatado\(\sqrt[n]{a^{n}}=|a|\).
\(\left|a^{m}\right|\)
Então\(\sqrt{a^{2 m}}=\left|a^{m}\right|\).
Nós aplicamos esse conceito no próximo exemplo.
Simplifique:
- \(\sqrt{x^{6}}\)
- \(\sqrt{y^{16}}\)
Solução:
uma.
\(\sqrt{x^{6}}\)
Desde\(\left(x^{3}\right)^{2}=x^{6}\).
\(\sqrt{\left(x^{3}\right)^{2}}\)
Já que o índice\(n\) é uniforme\(\sqrt{a^{n}}=|a|\).
\(\left|x^{3}\right|\)
b.
\(\sqrt{y^{16}}\)
Desde\(\left(y^{8}\right)^{2}=y^{16}\).
\(\sqrt{\left(y^{8}\right)^{2}}\)
Já que o índice\(n\) é uniforme\(\sqrt[n]{a^{n}}=|a|\).
\(y^{8}\)
Nesse caso, o sinal de valor absoluto não é necessário, pois\(y^{8}\) é positivo.
Simplifique:
- \(\sqrt{y^{18}}\)
- \(\sqrt{z^{12}}\)
- Responda
-
- \(|y^{9}|\)
- \(z^{6}\)
Simplifique:
- \(\sqrt{m^{4}}\)
- \(\sqrt{b^{10}}\)
- Responda
-
- \(m^{2}\)
- \(|b^{5}|\)
O próximo exemplo usa a mesma ideia para raízes mais altas.
Simplifique:
- \(\sqrt[3]{y^{18}}\)
- \(\sqrt[4]{z^{8}}\)
Solução:
uma.
\(\sqrt[3]{y^{18}}\)
Desde\(\left(y^{6}\right)^{3}=y^{18}\).
\(\sqrt[3]{\left(y^{6}\right)^{3}}\)
Já que\(n\) é estranho,\(\sqrt[n]{a^{n}}=a\).
\(y^{6}\)
b.
\(\sqrt[4]{z^{8}}\)
Desde\(\left(z^{2}\right)^{4}=z^{8}\).
\(\sqrt[4]{\left(z^{2}\right)^{4}}\)
Como\(z^{2}\) é positivo, não precisamos de um sinal de valor absoluto.
\(z^{2}\)
Simplifique:
- \(\sqrt[4]{u^{12}}\)
- \(\sqrt[3]{v^{15}}\)
- Responda
-
- \(|u^{3}|\)
- \(v^{5}\)
Simplifique:
- \(\sqrt[5]{c^{20}}\)
- \(\sqrt[6]{d^{24}}\)
- Responda
-
- \(c^{4}\)
- \(d^{4}\)
No próximo exemplo, agora temos um coeficiente na frente da variável. O conceito\(\sqrt{a^{2 m}}=\left|a^{m}\right|\) funciona praticamente da mesma maneira.
\(\sqrt{16 r^{22}}=4\left|r^{11}\right|\)porque\(\left(4 r^{11}\right)^{2}=16 r^{22}\).
Mas observe\(\sqrt{25 u^{8}}=5 u^{4}\) e nenhum sinal de valor absoluto é necessário, como sempre\(u^{4}\) é positivo.
Simplifique:
- \(\sqrt{16 n^{2}}\)
- \(-\sqrt{81 c^{2}}\)
Solução:
uma.
\(\sqrt{16 n^{2}}\)
Desde\((4 n)^{2}=16 n^{2}\).
\(\sqrt{(4 n)^{2}}\)
Já que o índice\(n\) é uniforme\(\sqrt[n]{a^{n}}=|a|\).
\(4|n|\)
b.
\(-\sqrt{81 c^{2}}\)
Desde\((9 c)^{2}=81 c^{2}\).
\(-\sqrt{(9 c)^{2}}\)
Já que o índice\(n\) é uniforme\(\sqrt[n]{a^{n}}=|a|\).
\(-9|c|\)
Simplifique:
- \(\sqrt{64 x^{2}}\)
- \(-\sqrt{100 p^{2}}\)
- Responda
-
- \(8|x|\)
- \(-10|p|\)
Simplifique:
- \(\sqrt{169 y^{2}}\)
- \(-\sqrt{121 y^{2}}\)
- Responda
-
- \(13|y|\)
- \(-11|y|\)
Este exemplo apenas leva a ideia mais longe, pois tem raízes de índices mais altos.
Simplifique:
- \(\sqrt[3]{64 p^{6}}\)
- \(\sqrt[4]{16 q^{12}}\)
Solução:
uma.
\(\sqrt[3]{64 p^{6}}\)
Reescreva\(64p^{6}\) como\(\left(4 p^{2}\right)^{3}\).
\(\sqrt[3]{\left(4 p^{2}\right)^{3}}\)
Pegue a raiz cúbica.
\(4p^{2}\)
b.
\(\sqrt[4]{16 q^{12}}\)
Reescreva o radicando como uma quarta potência.
\(\sqrt[4]{\left(2 q^{3}\right)^{4}}\)
Pegue a quarta raiz.
\(2|q^{3}|\)
Simplifique:
- \(\sqrt[3]{27 x^{27}}\)
- \(\sqrt[4]{81 q^{28}}\)
- Responda
-
- \(3x^{9}\)
- \(3|q^{7}|\)
Simplifique:
- \(\sqrt[3]{125 q^{9}}\)
- \(\sqrt[5]{243 q^{25}}\)
- Responda
-
- \(5p^{3}\)
- \(3q^{5}\)
Os próximos exemplos têm duas variáveis.
Simplifique:
- \(\sqrt{36 x^{2} y^{2}}\)
- \(\sqrt{121 a^{6} b^{8}}\)
- \(\sqrt[3]{64 p^{63} q^{9}}\)
Solução:
uma.
\(\sqrt{36 x^{2} y^{2}}\)
Desde\((6 x y)^{2}=36 x^{2} y^{2}\)
\(\sqrt{(6 x y)^{2}}\)
Pegue a raiz quadrada.
\(6|xy|\)
b.
\(\sqrt{121 a^{6} b^{8}}\)
Desde\(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)
\(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)
Pegue a raiz quadrada.
\(11\left|a^{3}\right| b^{4}\)
c.
\(\sqrt[3]{64 p^{63} q^{9}}\)
Desde\(\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}\)
\(\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}\)
Pegue a raiz cúbica.
\(4p^{21}q^{3}\)
Simplifique:
- \(\sqrt{100 a^{2} b^{2}}\)
- \(\sqrt{144 p^{12} q^{20}}\)
- \(\sqrt[3]{8 x^{30} y^{12}}\)
- Responda
-
- \(10|ab|\)
- \(12p^{6}q^{10}\)
- \(2x^{10}y^{4}\)
Simplifique:
- \(\sqrt{225 m^{2} n^{2}}\)
- \(\sqrt{169 x^{10} y^{14}}\)
- \(\sqrt[3]{27 w^{36} z^{15}}\)
- Responda
-
- \(15|mn|\)
- \(13\left|x^{5} y^{7}\right|\)
- \(3w^{12}z^{5}\)
Acesse esse recurso on-line para obter instruções e práticas adicionais com expressões simplificadas com raízes.
- Simplificando expoentes de variáveis com raízes usando valores absolutos
Conceitos chave
- Notação de raiz quadrada
- \(\sqrt{m}\)é lido como 'a raiz quadrada de\(m\) '
- E se\(n^{2}=m\), então\(n=\sqrt{m}\), para\(n≥0\).
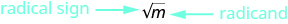
Figura 8.1.1 - A raiz quadrada de\(m\)\(\sqrt{m}\),, é um número positivo cujo quadrado é\(m\).
- Na raiz de um número
- Se\(b^{n}=a\), então\(b\) é uma\(n^{th}\) raiz de\(a\).
- A\(n^{th}\) raiz principal do\(a\) está escrita\(\sqrt[n]{a}\).
- \(n\)é chamado de índice do radical.
- Propriedades de\(\sqrt[n]{a}\)
- Quando\(n\) é um número par e
- \(a≥0\), então\(\sqrt[n]{a}\) é um número real
- \(a<0\), então não\(\sqrt[n]{a}\) é um número real
- Quando\(n\) é um número ímpar,\(\sqrt[n]{a}\) é um número real para todos os valores de\(a\).
- Quando\(n\) é um número par e
- Simplificando raízes pares e ímpares
- Para qualquer número inteiro\(n≥2\),
- quando\(n\) é estranho\(\sqrt[n]{a^{n}}=a\)
- quando\(n\) é par\(\sqrt[n]{a^{n}}=|a|\)
- Devemos usar os sinais de valor absoluto quando tomamos uma raiz uniforme de uma expressão com uma variável no radical.
- Para qualquer número inteiro\(n≥2\),
Glossário
- quadrado de um número
- Se\(n^{2}=m\), então\(m\) é o quadrado de\(n\).
- raiz quadrada de um número
- Se\(n^{2}=m\), então\(n\) é uma raiz quadrada de\(m\).


