2.7 : Exemples d'algèbre de vecteurs

Exemple\(\PageIndex{1}\): Analytical Computation of a Resultant

Trois vecteurs de déplacement\(\vec{A}\)\(\vec{B}\), et\(\vec{C}\) dans un plan (Figure 2.3.6) sont spécifiés par leurs magnitudes A = 10,0, B = 7,0 et C = 8,0, respectivement, et par leurs angles de direction respectifs avec la direction horizontale\(\alpha\) = 35°,\(\beta\) = −110°, et \(\gamma\)= 30°. Les unités physiques des magnitudes sont les centimètres. Résolvez les vecteurs en fonction de leurs composantes scalaires et trouvez les sommes vectorielles suivantes :

1. \(\vec{R}\)=\(\vec{A}\)\(\vec{B}\) +\(\vec{C}\),
2. \(\vec{D}\)=\(\vec{A}\) −\(\vec{B}\), et
3. \(\vec{S}\)=\(\vec{A}\) − 3\(\vec{B}\) +\(\vec{C}\).

Stratégie

Tout d'abord, nous utilisons l'équation 2.4.13 pour trouver les composantes scalaires de chaque vecteur, puis nous exprimons chaque vecteur dans sa forme de composante vectorielle donnée par\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}\). Ensuite, nous utilisons des méthodes analytiques d'algèbre vectorielle pour trouver les résultats.

Solution

Nous résolvons les vecteurs donnés en leurs composantes scalaires :

\[ \begin{cases} A_{x} = A \cos \alpha = (10.0\; cm) \cos {35^{o}} = 8.19\; cm \\ A_{y} = A \sin \alpha = (10.0\; cm) \sin{35^{o}} = 5.73\; cm \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \beta = (7.0\; cm) \cos (-110^{o}) = -2.39\; cm \\ B_{y} = B \sin \beta= (7.0\; cm) \sin (-110^{o}) = -6.58\; cm \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \gamma= (8.0\; cm) \cos (30^{o}) = 6.93\; cm \\ C_{y} = C \sin \gamma= (8.0\; cm) \sin(30^{o}) = 4.00\; cm \end{cases}\]

Pour (a), nous pouvons le remplacer directement dans l'équation 2.6.7 pour trouver les composantes scalaires de la résultante :

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = 8.19\; cm - 2.39\; cm + 6.93\; cm = 12.73\; cm \\ R_{y} = A_{y} + B_{y} + C_{y} = 5.73\; cm - 6.58\; cm + 4.00\; cm = 3.15\; cm \end{cases}\]

Par conséquent, le vecteur résultant est\(\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} = (12.7 \hat{i} + 3.1 \hat{j})\) cm. Pour (b), nous pouvons écrire la différence vectorielle comme

\[\vec{D} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j}) - (B_{x} \hat{i} + B_{y} \hat{j}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} \ldotp\]

Le vecteur de différence est donc\(\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (10.6 \hat{i} + 12.3 \hat{j})\) cm.

Pour (c), on peut écrire un vecteur\(\vec{S}\) sous la forme explicite suivante :

\[ \vec{S} = \vec{A} - 3 \vec{B} + \vec{C} = (A_{x} \hat{i} + A_{y} \hat{j}) - 3(B_{x} \hat{i} + B_{y} \hat{j}) + (C_{x} \hat{i} + C_{y} \hat{j}) = (A_{x} - 3 B_{x} + C_{x}) \hat{i} + (A_{y} - 3 B_{y} + C_{y}) \hat{j} \ldotp\]

Ensuite, les composants scalaires de\(\vec{S}\) sont

\[ \begin{cases} S_{x} = A_{x} - 3B_{x} + C_{x} = 8.19\; cm - 3(-2.39\; cm) + 6.93\; cm = 22.29\; cm \\ S_{y} = A_{y} - 3B_{y} + C_{y} = 5.73\; cm -3(-6.58\; cm) + 4.00\; cm = 29.47\; cm \end{cases}\]

Le vecteur est\(\vec{S} = S_{x} \hat{i} + S_{y} \hat{j} = (22.3 \hat{i} + 29.5 \hat{j})\) cm.

L'importance

Après avoir trouvé les composants vectoriels, nous pouvons illustrer les vecteurs par des graphiques ou nous pouvons calculer des magnitudes et des angles de direction, comme indiqué sur la figure\(\PageIndex{1}\). Les résultats pour les magnitudes en (b) et (c) peuvent être comparés aux résultats pour les mêmes problèmes obtenus avec la méthode graphique, illustrée à la Figure 2.3.7 et à la Figure 2.3.8. Notez que la méthode analytique produit des résultats exacts et que sa précision n'est pas limitée par la résolution d'une règle ou d'un rapporteur, comme c'était le cas avec la méthode graphique utilisée dans l'exemple 2.3.2 pour trouver ce même résultat.

Figure\(\PageIndex{1}\) : Illustration graphique des solutions obtenues de manière analytique.

Exercice 2.8

Trois vecteurs de déplacement\(\vec{A}\)\(\vec{B}\), et\(\vec{F}\) (Figure 2.3.6) sont spécifiés par leurs magnitudes A = 10,00, B = 7,00 et F = 20,00, respectivement, et par leurs angles de direction respectifs avec la direction horizontale\(\alpha\) = 35°,\(\beta\) = −110° et\(\varphi\) = 110 °. Les unités physiques des magnitudes sont les centimètres. Utilisez la méthode analytique pour trouver le vecteur\(\vec{F}\) =\(\vec{A}\) + 2\(\vec{B}\) −\(\vec{F}\). Vérifiez que G = 28,15 cm et que cela\(\theta_{G}\) = −68,65°.

Exemple\(\PageIndex{2}\): The Tug-of-War Game

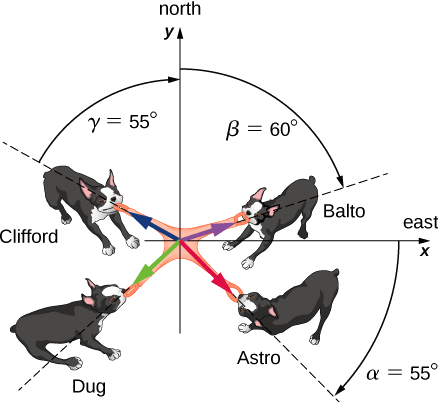
Quatre chiens nommés Astro, Balto, Clifford et Dug jouent à un jeu de tir à la corde avec un jouet (Figure\(\PageIndex{2}\)). Astro tire sur le jouet dans la direction\(\alpha\) = 55° au sud de l'est, Balto tire dans la direction\(\beta\) = 60° à l'est du nord et Clifford tire dans la direction\(\gamma\) = 55° à l'ouest du nord. Astro tire fortement avec 160,0 unités de force (N), que nous abrégeons en A = 160,0 N. Balto tire encore plus fort qu'Astro avec une force de magnitude B = 200,0 N, et Clifford tire avec une force de magnitude C = 140,0 N. Lorsque Dug tire sur le jouet de telle sorte que sa force équilibre la résultante du trois autres forces, le jouet ne se déplace dans aucune direction. Avec quelle force et dans quelle direction Dug doit-il tirer sur le jouet pour que cela se produise ?

Figure\(\PageIndex{2}\) : Quatre chiens jouent à un jeu de tir à la corde avec un jouet.

Stratégie

Nous supposons que l'est est la direction de l'axe X positif et le nord est la direction de l'axe y positif. Comme dans l'exemple\(\PageIndex{1}\), nous devons résoudre les trois forces données —\(\vec{A}\) (l'attraction d'Astro),\(\vec{B}\) (l'attraction de Balto) et\(\vec{C}\) (l'attraction de Clifford) — dans leurs composantes scalaires, puis trouver les composantes scalaires du vecteur résultant\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) + \(\vec{C}\). Lorsque la force\(\vec{D}\) de traction de Dug équilibre cette résultante, la somme de\(\vec{D}\) et\(\vec{R}\) doit donner le vecteur nul\(\vec{D}\) +\(\vec{R}\) =\(\vec{0}\). Cela signifie que\(\vec{D}\) =\(- \vec{R}\) donc l'attraction de Dug doit être antiparallèle à\(\vec{R}\).

Solution

Les angles de direction sont\(\theta_{A}\)\(− \alpha\) = = −55°,\(\theta_{B}\) = 90° −\(\beta\) = 30° et\(\theta_{C}\) = 90° +\(\gamma\) = 145°, et leur substitution dans l'équation 2.4.13 donne les composantes scalaires des trois forces données :

\[ \begin{cases} A_{x} = A \cos \theta_{A} = (160.0\; N) \cos (-55^{o}) = + 91.8\; N \\ A_{y} = A \sin \theta_{A} = (160.0\; N) \sin (-55^{o}) = -131.1\; N \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \theta_{B} = (200.0\; N) \cos 30^{o} = + 173.2\; N \\ B_{y} = B \sin \theta_{B} = (200.0\; N) \sin 30^{o} = + 100.0\; N \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \theta_{C} = (140.0\; N) \cos 145^{o} = -114.7\; N \\ C_{y} = C \sin \theta_{C} = (140.0\; N) \sin 145^{o} = + 80.3\; N \end{cases}\]

Nous calculons maintenant les composantes scalaires du vecteur résultant\(\vec{R} = \vec{A} + \vec{B} + \vec{C}\) :

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = + 91.8\; N+ 173.2\; N- 114.7\; N = +150.3 \; N\\ R_{y} = A_{y} + B_{y} + C_{y} = -131.1\; N + 100.0\; N + 80.3\; N= +49.2\; N\end{cases}\]

Le vecteur antiparallèle à la résultante\(\vec{R}\) est

\[\vec{D} = -\vec{R} = -R_{x} \hat{i} - R_{y} \hat{j} = (-150.3 \hat{i} - 49.2 \hat{j}) N \ldotp\]

L'ampleur de la force de traction de Dug est

\[D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{(-150.3)^{2} + (-49.2)^{2}} N = 158.1\; N \ldotp\]

La direction de la force de traction de Dug est

\[\theta = \tan^{-1} \left(\dfrac{D_{y}}{D_{x}}\right) = \tan^{-1} \left(\dfrac{-49.2\; N}{-150.3\; N}\right) = \tan^{-1} \left(\dfrac{49.2}{150.3}\right) = 18.1^{o}\ldotp\]

Le creusement tire dans la direction 18,1° au sud-ouest parce que les deux composantes sont négatives, ce qui signifie que le vecteur d'attraction se situe dans le troisième quadrant (Figure 2.4.4).

Exercice 2.9

Supposons que Balto dans Example\(\PageIndex{2}\) quitte le jeu pour s'occuper de questions plus importantes, mais qu'Astro, Clifford et Dug continuent à jouer. L'attraction d'Astro et Clifford sur le jouet ne change pas, mais Dug court et mord le jouet à un endroit différent. Avec quelle force et dans quelle direction Dug doit-il tirer sur le jouet maintenant pour contrebalancer les forces combinées de Clifford et Astro ? Illustrez cette situation en dessinant un diagramme vectoriel indiquant toutes les forces impliquées.

Exemple\(\PageIndex{3}\): Vector Algebra

Détermine l'amplitude du vecteur\(\vec{C}\) qui satisfait l'équation 2\(\vec{A}\) − 6\(\vec{B}\) + 3\(\vec{C}\) = 2\(\hat{j}\),\(\vec{A}\) =\(\hat{i}\) − 2\(\hat{k}\) et\(\vec{B}\) = −\(\hat{j}\) +\(\frac{\hat{k}}{2}\).

Stratégie

Nous résolvons d'abord l'équation donnée pour le vecteur inconnu\(\vec{C}\). Ensuite, nous substituons\(\vec{A}\) et\(\vec{B}\) regroupons les termes dans chacune des trois directions\(\hat{i}\)\(\hat{j}\), et\(\hat{k}\) ; et nous identifions les composantes scalaires C _x, C _y et C _z. Enfin, nous la substituons à l'équation 2.5.6 pour trouver la magnitude C.

Solution

\[\begin{split} 2 \vec{A} - 6 \vec{B} +& 3 \vec{C} = 2 \hat{j}\\ & 3 \vec{C} = 2 \hat{j} - 2 \vec{A} + 6 \vec{B} \\ &\vec{C} = \frac{2}{3} \hat{j} - \frac{2}{3} \vec{A} + 2 \vec{B}\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} (\hat{i} - 2\hat{k}) + 2 \big(- \hat{j} + \frac{\hat{k}}{2}\big)\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} \hat{i} + \frac{4}{3} \hat{k} - 2 \hat{j} + \hat{k}\\ & \quad = -\frac{2}{3} \hat{i} + \big(\frac{2}{3} - 2 \big)\hat{j} + \big(\frac{4}{3}\ + 1 \big)\hat{k}\\ & \quad = -\frac{2}{3} \hat{i} - \frac{4}{3} \hat{j} + \frac{7}{3} \hat{k} \end{split}\]

Les composantes sont C _x =\(-\frac{2}{3}\), C _y =\(-\frac{4}{3}\) et C _z =\(\frac{7}{3}\), et la substitution dans l'équation 2.5.6 donne

\[C = \sqrt{C_{x}^{2} + C_{y}^{2} + C_{z}^{2}} = \sqrt{\left(-\dfrac{2}{3}\right)^{2} + \left(-\dfrac{4}{3}\right)^{2} + \left(\dfrac{7}{3}\right)^{2}} = \sqrt{\frac{23}{3}} \ldotp\]

Exemple\(\PageIndex{4}\): Displacement of a Skier

Au départ d'un chalet de ski, un skieur de fond parcourt 5,0 km au nord, puis 3,0 km à l'ouest et enfin 4,0 km au sud-ouest avant de se reposer. Trouvez son vecteur de déplacement total par rapport à la loge lorsqu'il est au point de repos. À quelle distance et dans quelle direction doit-il skier depuis le point de repos pour rentrer directement au lodge ?

Stratégie

Nous supposons un système de coordonnées rectangulaires dont l'origine se trouve au chalet de ski et dont le vecteur unitaire\(\hat{i}\) pointe vers l'est et le vecteur unitaire\(\hat{j}\) vers le nord. Il existe trois déplacements :\(\vec{D}_{1}\),\(\vec{D}_{2}\), et\(\vec{D}_{3}\). Nous identifions leurs magnitudes comme suit : D ₁ = 5,0 km, D ₂ = 3,0 km et D ₃ = 4,0 km. Nous déterminons que leurs directions sont les angles\(\theta_{1}\)\(\theta_{2}\) = 90°, = 180° et\(\theta_{3}\) = 180° + 45° = 225°. Nous résolvons chaque vecteur de déplacement en ses composantes scalaires et les substituons dans l'équation 2.6.5 pour obtenir les composantes scalaires du déplacement\(\vec{D}\) résultant de la loge au point de repos. Sur le chemin du retour du point de repos au lodge, le déplacement est\(\vec{B}\) = −\(\vec{D}\). Enfin, nous trouvons la magnitude et la direction de\(\vec{B}\).

Solution

Les composantes scalaires des vecteurs de déplacement sont

\[ \begin{cases} D_{1x} = D_{1} \cos \theta_{1} = (5.0\; km) \cos 90^{o} = 0 \\ D_{1y} = D_{1} \sin \theta_{1} = (5.0\; km) \sin 90^{o} = 5.0\; km \end{cases}\]

\[ \begin{cases} D_{2x} = D_{2} \cos \theta_{2} = (3.0\; km) \cos 180^{o} = -3.0 \;km\\ D_{2y} = D_{2} \sin \theta_{2} = (3.0\; km) \sin 180^{o} = 0 \end{cases}\]

\[ \begin{cases} D_{3x} = D_{3} \cos \theta_{3} = (4.0\; km) \cos 225^{o} = -2.8\; km \\ D_{3y} = D_{3} \sin \theta_{3} = (4.0\; km) \sin 225^{o} = -2.8\; km \end{cases}\]

Les composantes scalaires du vecteur de déplacement net sont

\[ \begin{cases} D_{x} = D_{1x} + D_{2x} + D_{3x} = (0 - 3.0 - 2.8)km = -5.8\; km \\ D_{y} = D_{1y} + D_{2y} + D_{3y} = (5.0 + 0 - 2.8)km = + 2.2\; km \end{cases}\]

Ainsi, le vecteur de déplacement net du skieur est\(\vec{D}\) = D _x\(\hat{i}\) + D _y\(\hat{j}\) = (−5,8\(\hat{i}\) + 2,2\(\hat{j}\)) km. Sur le chemin du retour au lodge, son déplacement est de\(\vec{B}\) = −\(\vec{D}\) = − (−5,8\(\hat{i}\) + 2,2\(\hat{j}\)) km = (5,8\(\hat{i}\) − 2,2\(\hat{j}\)) km. Sa magnitude est B =\(\sqrt{B_{x}^{2} + B_{y}^{2}}\) =\(\sqrt{(5.8)^{2} + (−2.2)^{2}}\) km = 6,2 km et son angle de direction est\(\theta\) = tan ⁻¹\(\left(\dfrac{−2.2}{5.8}\right)\) = −20,8°. Par conséquent, pour regagner le lodge, il doit parcourir 6,2 km dans une direction d'environ 21° au sud de l'est.

L'importance

Notez qu'aucun chiffre n'est nécessaire pour résoudre ce problème par la méthode analytique. Des figures sont nécessaires lorsque vous utilisez une méthode graphique ; toutefois, nous pouvons vérifier si notre solution a du sens en l'esquissant, ce qui constitue une étape finale utile pour résoudre tout problème vectoriel.

Exemple\(\PageIndex{5}\): Displacement of a Jogger

Un joggeur monte une volée de 200 marches identiques jusqu'au sommet d'une colline, puis court le long du sommet de la colline à 50,0 m avant de s'arrêter à une fontaine (Figure\(\PageIndex{3}\)). Son vecteur de déplacement du point A au bas des marches jusqu'au point B de la fontaine est\(\vec{D}_{AB}\) = (−90,0\(\hat{i}\) + 30,0\(\hat{j}\)) m. Quelles sont la hauteur et la largeur de chaque pas du vol ? Quelle est la distance réelle parcourue par le joggeur ? S'il fait une boucle et revient au point A, quel est son vecteur de déplacement net ?

Figure\(\PageIndex{3}\) : Un joggeur monte une volée de marches.

Stratégie

Le vecteur de déplacement\(\vec{D}_{AB}\) est la somme vectorielle du vecteur de déplacement du joggeur le\(\vec{D}_{AT}\) long des escaliers (du point A en bas de l'escalier au point T en haut de l'escalier) et de son vecteur\(\vec{D}_{RB}\) de déplacement en haut de la colline (du point T en haut de l'escalier jusqu'au fontaine au point B). Nous devons trouver les composantes horizontales et verticales de\(\vec{D}_{TB}\). Si chaque marche a une largeur w et une hauteur h, la composante horizontale de\(\vec{D}_{TB}\) doit avoir une longueur de 200 w et la composante verticale doit avoir une longueur de 200 h. La distance réelle parcourue par le joggeur est la somme de la distance qu'il court pour monter les escaliers et de la distance de 50 m qu'il parcourt le long du sommet de la colline.

Solution

Dans le système de coordonnées indiqué sur la figure\(\PageIndex{3}\), le vecteur de déplacement du joggeur au sommet de la colline est\(\vec{D}_{RB}\) = (−50,0 m)\(\hat{i}\). Son vecteur de déplacement net est

\[\vec{D}_{AB} = \vec{D}_{AT} + \vec{D}_{TB} \ldotp \nonumber\]

Par conséquent, son vecteur de déplacement\(\vec{D}_{TB}\) le long des escaliers est

\[\begin{split} \vec{D}_{AT}& = \vec{D}_{AB} - \vec{D}_{TB} = (-90.0 \hat{i} + 30.0 \hat{j})m - (-50.0 m)\hat{i}) = [(-90.0 50.0) hat{i} + 30.0 \hat{j})]m \\ & = (-40.0 \hat{i} + 30.0 \hat{j})m \ldotp \end{split}\]

Ses composantes scalaires sont D _ATx = −40,0 m et D _ATy = 30,0 m. Par conséquent, nous devons avoir

\[200 w=|-40.0| \mathrm{m} \text { and } 200 h=30.0 \: \mathrm{m} \ldotp \nonumber\]

Ainsi, la largeur du pas est w\(\frac{40.0\; m}{200}\) = 0,2 m = 20 cm et la hauteur du pas est w\(\frac{30.0\; m}{200}\) = 0,15 m = 15 cm. La distance parcourue par le joggeur le long des escaliers est

\[\vec{D}_{AT} = \sqrt{\vec{D}_{ATx}^{2} + \vec{D}_{ATy}^{2}} = \sqrt{(-40.0)^{2} + (30.0)^{2}}m = 50.0\; m \ldotp \nonumber\]

Ainsi, la distance réelle qu'il parcourt est D _AT + D _TB = 50,0 m + 50,0 m = 100,0 m. Lorsqu'il fait une boucle et revient de la fontaine à sa position initiale au point A, la distance totale qu'il parcourt est le double de cette distance, soit 200,0 m. Cependant, son vecteur de déplacement net est nul, car lorsque sa position finale est la même que sa position initiale, les composantes scalaires de son vecteur de déplacement net sont nulles (Équation 2.4.4).

Dans de nombreuses situations physiques, nous avons souvent besoin de connaître la direction d'un vecteur. Par exemple, nous pouvons vouloir connaître la direction d'un vecteur de champ magnétique à un moment donné ou la direction du mouvement d'un objet. Nous avons déjà dit que la direction est donnée par un vecteur unitaire, qui est une entité sans dimension, c'est-à-dire qu'aucune unité physique ne lui est associée. Lorsque le vecteur en question se trouve le long de l'un des axes d'un système de coordonnées cartésien, la réponse est simple, car son vecteur de direction unitaire est alors soit parallèle soit antiparallèle à la direction du vecteur unitaire d'un axe. Par exemple, la direction du vecteur\(\vec{d}\) = -5 m\(\hat{i}\) est le vecteur unitaire\(\vec{d}\) = -\(\hat{i}\). La règle générale pour trouver le vecteur\(\vec{V}\) de direction unitaire d'un vecteur\(\vec{V}\) est de le diviser par sa magnitude V :

\[\widehat{\mathbf{V}}=\frac{\overrightarrow{\mathbf{V}}}{V} \label{2.26} \cdot \]

Cette expression montre que le vecteur unitaire de direction est effectivement sans dimension car le numérateur et le dénominateur de l'équation \ ref {2.26} ont la même unité physique. De cette façon, l'équation \ ref {2.26} nous permet d'exprimer le vecteur unitaire de direction en termes de vecteurs unitaires des axes. L'exemple suivant illustre ce principe.

Exemple\(\PageIndex{6}\): The Unit Vector of Direction

Si le vecteur de vitesse du convoi militaire dans l'exemple 2.6.1 est\(\vec{v}\) = (4 000\(\hat{i}\) + 3 000\(\hat{j}\) + 0,100\(\hat{k}\)) km/h, quel est le vecteur unitaire de sa direction de mouvement.

Stratégie

Le vecteur unitaire de la direction du mouvement du convoi est\(\hat{v}\) le vecteur unitaire parallèle au vecteur vitesse. Le vecteur unitaire est obtenu en divisant un vecteur par sa magnitude, conformément à l'équation \ ref {2.26}.

Solution

L'amplitude du vecteur\(\vec{v}\) est

\[v = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} = \sqrt{4.000^{2} + 3.000^{2} + 0.100^{2}}km/h = 5.001\; km/h \ldotp \nonumber\]

Pour obtenir le vecteur unitaire\(\hat{v}\), divisez\(\vec{v}\) par sa magnitude :

\[\begin{split} \hat{v}& = \frac{\vec{v}}{v} = \frac{(4.000 \hat{i} + 3.00 \hat{j} + 0.100 \hat{k})km/h}{5.001\; km/h} \\ & = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.1100 \hat{k})}{5.001} \\ & = \frac{4.000}{5.001} \hat{i} + \frac{3.000}{5.001} \hat{j} + \frac{0.100}{5.001} \hat{k} \\ & = (79.98 \hat{i} + 59.99 \hat{j} + 2.00 \hat{k}) \times 10^{-2} \ldotp \end{split}\]

L'importance

Notez que lorsque vous utilisez la méthode d'analyse avec une calculatrice, il est conseillé d'effectuer vos calculs à au moins trois décimales, puis d'arrondir la réponse finale au nombre de chiffres significatifs requis, comme nous avons effectué les calculs dans cet exemple. Si vous arrondissez votre réponse partielle trop tôt, vous risquez que votre réponse finale comporte une énorme erreur numérique, et elle peut être loin de la réponse exacte ou d'une valeur mesurée lors d'une expérience.

Exercice 2.10

Vérifiez que le vecteur\(\hat{v}\) obtenu dans l'exemple\(\PageIndex{3}\) est bien un vecteur unitaire en calculant sa magnitude. Si le convoi de l'exemple 2.6.1 se déplaçait sur une plaine désertique, c'est-à-dire si la troisième composante de sa vitesse était nulle, quel est le vecteur unitaire de sa direction de mouvement ? Quelle direction géographique représente-t-il ?