17.1E : Exercices pour la section 17.1

Last updated
Save as PDF

Page ID: 197542

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 6, classez chacune des équations suivantes comme étant linéaires ou non linéaires. Si l'équation est linéaire, déterminez si elle est homogène ou non homogène.

1. $x^3y''+(x-1)y'-8y=0$

Réponse: linéaire, homogène

2. $(1+y^2)y''+xy'-3y= \cos x$

3. $xy''+e^yy'=x$

Réponse: non linéaire

4. $y''+ \dfrac{4}{x}y'-8xy=5x^2+1 $

5. $y''+( \sin x)y'-xy=4y $

Réponse: linéaire, homogène

6. $y''+\left(\dfrac{x+3}{y}\right)y'=0$

Dans les exercices 7 à 10, vérifiez que la fonction donnée est une solution à l'équation différentielle. Utilisez un utilitaire de création graphique pour représenter graphiquement les solutions particulières pour plusieurs valeurs de$c_1$ et$c_2.$ Qu'est-ce que les solutions ont en commun ?

7. [T]$y''+2y'-3y=0; \quad y(x)=c_1e^x+c_2e^{-3x}$

8. [T]$x^2y''-2y-3x^2+1=0; \quad y(x)=c_1x^2+c_2x^{-1}+x^2 \ln(x)+ \frac{1}{2} $

9. [T]$y''+14y+49y=0; \quad y(x)=c_1e^{−7x}+c_2xe^{−7x}$

10. [T]$6y''−49y′+8y=0; \quad y(x)=c_1e^{x/6}+c_2e^{8x}$

Dans les exercices 11 à 30, trouvez la solution générale à l'équation différentielle linéaire.

11. $y''−3y′−10y=0$

Réponse: $y = c_1e^{5x} + c_2e^{-2x}$

12. $y''−7y′+12y=0$

13. $y''+4y′+4y=0$

Réponse: $y = c_1e^{-2x} + c_2xe^{-2x}$

14. $4y''−12y′+9y=0$

15. $2y''−3y′−5y=0$

Réponse: $y = c_1e^{5x/2} + c_2e^{-x}$

16. $3y''−14y′+8y=0$

17. $y''+y′+y=0$

Réponse: $y = e^{-x/2}\left(c_1\cos\frac{\sqrt{3}x}{2} + c_2\sin\frac{\sqrt{3}x}{2}\right)$

18. $5y''+2y′+4y=0$

19. $y''−121y=0$

Réponse: $y = c_1e^{-11x} + c_2e^{11x}$

20. $8y''+14y′−15y=0$

21. $y''+81y=0$

Réponse: $y = c_1\cos 9x + c_2\sin 9x$

22. $y''−y′+11y=0$

23. $2y''=0$

Réponse: $y = c_1 + c_2x$

24. $y''−6y′+9y=0$

25. $3y''−2y′−7y=0$

Réponse: $y = c_1e^{\left( (1+\sqrt{22})/3 \right)x} + c_2e^{\left( (1-\sqrt{22})/3 \right)x}$

26. $4y''−10y′=0$

27. $36\dfrac{d^2y}{dx^2}+12\dfrac{dy}{dx}+y=0$

Réponse: $y = c_1e^{-x/6} + c_2xe^{-x/6}$

28. $25\dfrac{d^2y}{dx^2}−80\dfrac{dy}{dx}+64y=0$

29. $\dfrac{d^2y}{dx^2}−9\dfrac{dy}{dx}=0$

Réponse: $y = c_1 + c_2e^{9x}$

30. $4\dfrac{d^2y}{dx^2}+8y=0$

Dans les exercices 31 à 38, résolvez le problème de la valeur initiale.

31. $y''+5y′+6y=0, \quad y(0)=0,\; y′(0)=−2$

Réponse: $y = -2e^{-2x} + 2e^{-3x}$

32. $y''+2y′−8y=0, \quad y(0)=5,\; y′(0)=4$

33. $y''+4y=0, \quad y(0)=3, \; y′(0)=10$

Réponse: $y = 3\cos(2x) + 5\sin(2x)$

34. $y''−18y′+81y=0, \quad y(0)=1, \; y′(0)=5 $

35. $y''−y′−30y=0, \quad y(0)=1, \; y′(0)=−16$

Réponse: $y = -e^{6x} + 2e^{-5x}$

36. $4y''+4y′−8y=0, \quad y(0)=2, \; y′(0)=1$

37. $25y''+10y′+y=0, \quad y(0)=2, \; y′(0)=1$

Réponse: $y = 2e^{-x/5} + \frac{7}{5}xe^{-x/5}$

38. $y''+y=0, \quad y(π)=1, \; y′(π)=−5$

Dans les exercices 39 à 46, résolvez le problème des valeurs limites, si possible.

39. $y''+y′−42y=0, \quad y(0)=0, \; y(1)=2$

Réponse: $y = \left( \frac{2}{e^6 - e^{-7}} \right)e^{6x} - \left( \frac{2}{e^6 - e^{-7}} \right)e^{-7x}$

40. $9y''+y=0, \quad y(3π^2)=6, \; y(0)=−8$

41. $y''+10y′+34y=0, \quad y(0)=6, \; y(π)=2$

Réponse: Aucune solution n'existe.

42. $y''+7y′−60y=0, \quad y(0)=4, \; y(2)=0$

43. $y''−4y′+4y=0, \quad y(0)=2, \; y(1)=−1$

Réponse: $y = 2e^{2x} - \left( \frac{2e^{2}+1}{e^2} \right)xe^{2x}$

44. $y''−5y′=0, \quad y(0)=3, \; y(−1)=2$

45. $y''+9y=0, \quad y(0)=4, \; y(π^3)=−4$

Réponse: $y = 4\cos 3x + c_2\sin 3x,$une infinité de solutions

46. $4y''+25y=0, \quad y(0)=2, \; y(2π)=−2$

47. Trouvez une équation différentielle avec une solution générale qui est$y=c_1e^{x/5}+c_2e^{−4x}.$

Réponse: $5y'' +19y' -4y = 0$

48. Trouvez une équation différentielle avec une solution générale qui est$y=c_1e^{x}+c_2e^{−4x/3}.$

Pour chaque équation différentielle des exercices 49 à 51 :

Résolvez le problème de valeur initiale.
[T] Utilisez un utilitaire de création graphique pour représenter graphiquement la solution en question.

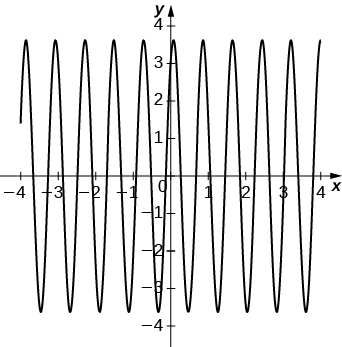
49. $y''+64y=0; \quad y(0)=3, \; y′(0)=16$

Réponse: a.$y = 3\cos 8x + 2\sin 8x$
b.
$Cette figure est un graphique périodique. Il a une amplitude de 3,5. Les axes x et y sont redimensionnés par incréments de 1.$

50. $y''−2y′+10y=0; \quad y(0)=1, \; y′(0)=13$

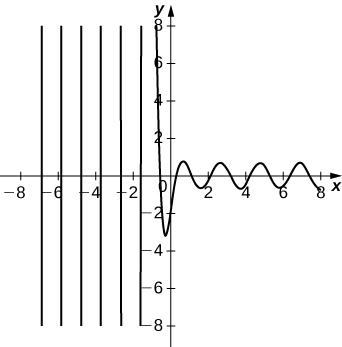
51. $y''+5y′+15y=0; \quad y(0)=−2, \; y′(0)=7$

Réponse: a.$y = e^{-5/2}\left[-2\cos\left(\frac{\sqrt{35}}{2}x\right) + \frac{4\sqrt{35}}{35}\sin\left(\frac{\sqrt{35}}{2}x\right) \right]$
b.
$Cette figure est un graphique d'une fonction oscillante. Les axes x et y sont redimensionnés par incréments de nombres pairs. L'amplitude du graphe diminue à mesure que x augmente.$

52. (Principe de superposition) Prouvez que si$y_1(x)$ et$y_2(x)$ sont des solutions à une équation différentielle homogène linéaire,$y''+p(x)y′+q(x)y=0,$ alors la fonction$y(x)=c_1y_1(x)+c_2y_2(x),$ où$c_1$ et$c_2$ sont des constantes est également une solution.

53. Prouvez que si$a, \, b$ et$c$ sont des constantes positives, alors toutes les solutions à l'équation différentielle linéaire du second ordre s'$ay''+by′+cy=0$approchent de zéro comme$x→∞.$ (Conseil : considérez trois cas : deux racines distinctes, des racines réelles répétées et des racines conjuguées complexes.)