17.1 : Équations linéaires du second ordre
- Page ID
- 197529
- Reconnaître les équations différentielles linéaires homogènes et non homogènes
- Déterminez l'équation caractéristique d'une équation linéaire homogène.
- Utilisez les racines de l'équation caractéristique pour trouver la solution à une équation linéaire homogène.
- Résolvez les problèmes de valeur initiale et de valeur limite impliquant des équations différentielles linéaires.
Lorsque vous travaillez avec des équations différentielles, l'objectif est généralement de trouver une solution. En d'autres termes, nous voulons trouver une fonction (ou des fonctions) qui satisfait à l'équation différentielle. La technique que nous utilisons pour trouver ces solutions varie en fonction de la forme de l'équation différentielle avec laquelle nous travaillons. Les équations différentielles du second ordre présentent plusieurs caractéristiques importantes qui peuvent nous aider à déterminer la méthode de solution à utiliser. Dans cette section, nous examinons certaines de ces caractéristiques et la terminologie associée.
équations linéaires homogènes
Considérez l'équation différentielle du second ordre
\[xy''+2x^2y'+5x^3y=0.\nonumber \]
Remarquez que cela\(y\) et ses dérivés apparaissent sous une forme relativement simple. Ils sont multipliés par les fonctions des pouvoirs eux-mêmes\(x\), mais ils ne sont pas élevés à des puissances elles-mêmes, et ils ne sont pas non plus multipliés ensemble. Comme indiqué précédemment, les équations de premier ordre présentant des caractéristiques similaires sont dites linéaires. Il en va de même pour les équations du second ordre. Notez également que tous les termes de cette équation différentielle impliquent l'une ou l'autre de ses dérivées\(y\) ou l'une d'entre elles. Il n'existe pas de termes impliquant uniquement les fonctions de\(x\). Les équations de ce type, dans lesquelles chaque terme contient\(y\) ou l'un de ses dérivés, sont dites homogènes.
Certaines équations différentielles ne sont pas homogènes. Considérez l'équation différentielle
\[xy''+2x^2y'+5x^3y=x^2.\nonumber \]
Le\(x^2\) terme situé sur le côté droit du signe égal ne contient\(y\) aucun de ses dérivés. Cette équation différentielle n'est donc pas homogène.
Une équation différentielle du second ordre est linéaire si elle peut être écrite sous la forme
\[a_{2}(x)y''+a){1}(x)y'+a_{0}(x)y=r(x), \label{17.1} \]
où\(a_{2}(x), a_{1}(x), a_{0}(x),\) et\(r(x)\) sont des fonctions à valeur réelle et\(a_{2}(x)\) ne sont pas identiques à zéro. Si\(r(x) \equiv 0\) —en d'autres termes, si\(r(x)=0\) pour chaque valeur de\(x\) —on dit que l'équation est une équation linéaire homogène. Si\(r(x) \neq 0\) pour une certaine valeur de\(x,\) l'équation, on dit qu'il s'agit d'une équation linéaire non homogène.
Dans les équations différentielles linéaires,\(y\) ses dérivées ne peuvent être élevées qu'à la première puissance et elles ne peuvent pas être multipliées les unes par les autres. Termes impliquant\(y^2\) ou\(\sqrt{y'}\) rendant l'équation non linéaire. Les fonctions de\(y\) et leurs dérivées, telles que\(\sin y\) ou\(e^{y'}\), sont également interdites dans les équations différentielles linéaires.
Notez que les équations peuvent ne pas toujours être données sous forme standard (la forme indiquée dans la définition). Il peut être utile de les réécrire sous cette forme pour décider s'ils sont linéaires ou si une équation linéaire est homogène.
Classez chacune des équations suivantes comme étant linéaires ou non linéaires. Si l'équation est linéaire, déterminez ensuite si elle est homogène ou non homogène.
- \(y''+3x^4y'+x^2y^2=x^3\)
- \((\sin x)y''+(\cos x)y'+3y=0\)
- \(4t^2x''+3txx'+4x=0\)
- \(5y''+y=4x^5 \)
- \(( \cos x)y''- \sin y'+( \sin x)y- \cos x=0\)
- \(8ty''-6t^2y'+4ty-3t^2=0 \)
- \( \sin(x^2)y''-( \cos x)y'+x^2y=y'-3 \)
- \(y''+5xy'-3y= \cos y\)
Solution
- Cette équation n'est pas linéaire à cause du\(y^2\) terme.
- Cette équation est linéaire. Aucun terme n'implique une puissance ou une fonction de\(y,\) et les coefficients sont tous des fonctions de\(x\). L'équation est déjà écrite sous forme standard et\(r(x)\) est identique à zéro, de sorte que l'équation est homogène.
- Cette équation n'est pas linéaire. Notez que, dans ce cas,\(x\) il s'agit de la variable dépendante et\(t\) de la variable indépendante. Le second terme implique le produit de\(x\) et\(x'\), donc l'équation n'est pas linéaire.
- Cette équation est linéaire. Puisque\(r(x)=4x^5,\) l'équation n'est pas homogène.
- Cette équation n'est pas linéaire, à cause du\(\sin y'\) terme.
- Cette équation est linéaire. Le réécrire sous forme standard donne
\[8t^2y''-6t^2y'+4ty=3t^2. \nonumber \]
Avec l'équation sous forme standard, nous pouvons voir que l'équation n'est\(r(t)=3t^2,\) donc pas homogène. - Cette équation semble linéaire, mais nous devons la réécrire sous une forme standard pour en être sûre. Nous obtenons
\[ \sin(x^2)y''-(\cos x+1)y'+x^2y=-3. \nonumber \]
Cette équation est en effet linéaire. Avec\(r(x)=-3,\) elle, elle n'est pas homogène. - Cette équation n'est pas linéaire à cause du\(\cos y\) terme.
Classez chacune des équations suivantes comme étant linéaires ou non linéaires. Si l'équation est linéaire, déterminez ensuite si elle est homogène ou non homogène.
- \((y'')2-y'+8x^3y=0\)
- \((\sin t)y''+ \cos t-3ty'=0\)
- Allusion
-
Écrivez l'équation sous forme standard (Équation \ ref {17.1}) si nécessaire. Vérifiez les pouvoirs ou les fonctions de\(y\) et de ses dérivés.
- Répondez à une
-
Linéaire non linéaire
- Réponse b
-
non homogène
Plus loin dans cette section, nous verrons quelques techniques permettant de résoudre des types spécifiques d'équations différentielles. Avant d'y arriver, voyons comment se comportent les solutions aux équations différentielles linéaires. Dans de nombreux cas, pour résoudre des équations différentielles, il faut faire des suppositions éclairées sur ce à quoi pourrait ressembler la solution. Il sera utile de connaître le comportement des différents types de solutions.
Considérez l'équation différentielle linéaire et homogène
\[x^2y''-xy′-3y=0. \nonumber \]
En regardant cette équation, remarquez que les fonctions des coefficients sont des polynômes, avec des puissances plus élevées\(x\) associées à des dérivées d'ordre supérieur de\(y\). Montrez que\(y=x^3\) c'est une solution à cette équation différentielle.
Solution
\(y'=3x^2\)Let\(y=x^3.\) Then et en\(y''=6x.\) substituant dans l'équation différentielle, nous voyons que
\[\begin{align*} x^2y''-xy'-3y &=x^2(6x)-x(3x^2)-3(x^3) \\[4pt] &=6x^3-3x^3-3x^3 \\[4pt] &=0. \end{align*}\]
Montrez que\(y=2x^2\) c'est une solution à l'équation différentielle
\[\dfrac{1}{2}x^2y''-xy'+y=0. \label{ex2} \]
- Allusion
-
Calculez les dérivées et remplacez-les dans l'équation différentielle.
- Réponse
-
Cela nécessite de calculer\(y'\) et\(y''\).
\[y' = \dfrac{dy}{dx} = 4x \nonumber \]
et
\[ y'' = \dfrac{dy'}{dx} = 4 \nonumber \]
Insertion de ces dérivées\(y=2x^2\) dans l'équation \ ref {ex2}.
\[\begin{align*} \dfrac{1}{2}x^2y''-xy'+y &\overset{?}{=} 0 \\[4pt] \dfrac{1}{2}x^2(4) - x (4x) + 2x^2 &\overset{?}{=} 0 \\[4pt] 2x^2 - 4x^2 + 2x^2 &\overset{\checkmark}{=} 0 \end{align*} \nonumber \]
Oui, il s'agit d'une solution à l'équation différentielle de l'équation \ ref {ex2}.
Bien qu'il soit important de simplement trouver une solution à une équation différentielle, les mathématiciens et les ingénieurs souhaitent souvent aller au-delà de la recherche d'une seule solution à une équation différentielle pour trouver toutes les solutions à une équation différentielle. En d'autres termes, nous voulons trouver une solution générale. Tout comme pour les équations différentielles du premier ordre, une solution générale (ou famille de solutions) donne l'ensemble des solutions à une équation différentielle. Une différence importante entre les équations du premier ordre et celles du second ordre est que, pour les équations du second ordre, nous devons généralement trouver deux solutions différentes à l'équation pour trouver la solution générale. Si nous trouvons deux solutions, alors toute combinaison linéaire de ces solutions est également une solution. Nous affirmons ce fait sous la forme du théorème suivant.
Si\(y_1(x)\) et\(y_2(x)\) sont des solutions à une équation différentielle homogène linéaire, alors la fonction
\[y(x)=c_1y_1(x)+c_2y_2(x), \label{super} \]
où\(c_1\) et\(c_2\) sont des constantes, est également une solution.
La preuve de ce théorème du principe de superposition est laissée à titre d'exercice.
Considérez l'équation différentielle
\[y''-4y'-5y=0.\nonumber \]
Étant donné que\(e^{-x}\) et\(e^{5x}\) qu'il s'agit de solutions à cette équation différentielle, montrez que\(4e^{-x}+e^{5x}\) c'est une solution.
Solution
Bien que cela puisse être fait par une simple application du principe de superposition (équation \ ref {super}), nous pouvons également confirmer qu'il s'agit d'une solution via une approche comme dans Example\(\PageIndex{2}\). Nous avons
\[ \begin{align*} y(x) &=4e^{-x}+e^{5x} \\[4pt] y'(x) &= -4e^{-x} + 5e^{5x} \\[4pt] y''(x) &=4e^{-x}+25e^{5x}. \end{align*}\]
Alors
\[\begin{align*} y''-4y'-5y &\overset{?}{=} (4e^{-x}+25e^{5x})-4(-4e^{-x}+5e^{5x})-5(4e^{-x}+e^{5x}) \\[4pt] &\overset{?}{=} 4e^{-x}+25e^{5x}+16e^{-x}-20e^{5x}-20e^{-x}-5e^{5x} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
C'\(y(x)=4e^{-x}+e^{5x}\)est donc une solution.
Considérez l'équation différentielle
\[y''+5y'+6y=0. \nonumber \]
Étant donné que\(e^{-2x}\) et\(e^{-3x}\) qu'il s'agit de solutions à cette équation différentielle, montrez que\(3e^{-2x}+6e^{-3x}\) c'est une solution.
- Allusion
-
Différenciez la fonction et remplacez-la dans l'équation différentielle.
- Réponse
-
Bien que cela puisse être une simple application du principe de superposition (équation \ ref {super}), nous pouvons également le définir comme dans Example\(\PageIndex{2}\). Nous avons
\[ \begin{align*} y(x) &=3e^{-2x}+6e^{-3x} \\[4pt] y'(x) &= -6 e^{-2x} - 18e^{-3x} \\[4pt] y''(x) &= 12e^{-2x} + 54e^{3x}. \end{align*}\]
Alors
\[\begin{align*} y''+5y'+6y &= (12e^{-2x} + 54e^{3x}) + 5( -6 e^{-2x} - 18e^{-3x} ) + 6( 3e^{-2x} + 6e^{3x}) \\[4pt] &\overset{?}{=} \cancel{12e^{-2x}} + \bcancel{54e^{3x}} - \cancel{30e^{-2x}} - \bcancel{90e^{3x}} + \cancel{18e^{-2x}} + \bcancel{36e^{3x}} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
Ainsi,\(3e^{-2x}+6e^{-3x}\) est une solution à l'équation différentielle
Malheureusement, pour trouver la solution générale à une équation différentielle du second ordre, il ne suffit pas de trouver deux solutions puis de les combiner. Considérez l'équation différentielle
\[x''+7x'+12x=0.\nonumber \]
Les deux\(2e^{-3t}\) sont\(e^{-3t}\) des solutions (vous pouvez vérifier cela). Toutefois,
\[x(t)=c_1e^{-3t}+c_2(2e^{-3t})\nonumber \]
n'est pas la solution générale. Cette expression ne tient pas compte de toutes les solutions à l'équation différentielle. En particulier, il ne tient pas compte de la fonction\(e^{-4t},\) qui est également une solution à l'équation différentielle. Il s'avère que pour trouver la solution générale à une équation différentielle du second ordre, il faut trouver deux solutions linéairement indépendantes. Nous définissons cette terminologie ici.
Un ensemble de fonctions\(f_1(x),\, f_2(x), \ldots ,f_n(x)\) est considéré comme dépendant linéairement s'il existe des constantes\(c_1,\, c_2, \ldots c_n,\), pas toutes nulles, telles que
\[c_1f_1(x)+c_2f_2(x)+ \cdots +c_nf_n(x)=0 \nonumber \]
pour tout l'\(x\)intervalle d'intérêt. Un ensemble de fonctions qui n'est pas linéairement dépendant est dit linéairement indépendant.
Dans ce chapitre, nous testons généralement des ensembles de deux fonctions uniquement pour vérifier leur indépendance linéaire, ce qui nous permet de simplifier cette définition. D'un point de vue pratique, nous voyons que deux fonctions sont linéairement dépendantes si l'une d'elles est identique à zéro ou si elles sont des multiples constants l'une de l'autre.
Nous montrons d'abord que si les fonctions répondent aux conditions données précédemment, elles sont linéairement dépendantes. Si l'une des fonctions est identique à zéro,\(f_2(x) \equiv 0\) disons,, alors choisissez\(c_1=0\) et\(c_2=1,\) et la condition de dépendance linéaire est satisfaite. Si, par contre, ni l'un\(f_1(x)\) ni l'autre n'\(f_2(x)\)est identique à zéro, sauf\(f_1(x)=Cf_2(x)\) pour une constante,\(C,\) choisissez\(c_1=C\)\(c_2=-1,\) et encore une fois, la condition est satisfaite.
Ensuite, nous montrons que si deux fonctions sont linéairement dépendantes, alors soit l'une est identique à zéro, soit elles sont des multiples constants l'une de l'autre. Supposons\(f_1(x)\) et\(f_2(x)\) sont linéairement indépendants. Ensuite, il y a des constantes,\(c_1\) et\(c_2,\) non des deux nuls, de telle sorte que
\[c_1f_1(x)+c_2f_2(x)=0 \nonumber \]
pour tout l'\(x\)intervalle d'intérêt. Ensuite,
\[c_1f_1(x)=-c_2f_2(x). \nonumber \]
Maintenant, puisque nous avons déclaré que\(c_1\) les deux ne\(c_2\) peuvent pas être nuls, supposons\(c_2 \neq 0.\) alors, il y a deux cas : soit,\(c_1=0\) soit\(c_1\neq 0.\) si\(c_1=0,\) alors
\[\begin{align*} 0 &=-c_2f_2(x) \\[4pt] 0 &=f_2(x), \end{align*}\]
donc l'une des fonctions est identique à zéro. Supposons maintenant\(c_1 \neq 0.\) que,
\[f_1(x)=\left(- \dfrac{c_2}{c_1}\right)f_2(x) \nonumber \]
et nous voyons que les fonctions sont des multiples constants les unes des autres.
Deux fonctions,\(f_1(x)\) et\(f_2(x),\) sont dites dépendantes linéairement si l'une d'elles est identique à zéro ou s'il s'\(f_1(x)=Cf_2(x)\)agit d'une constante\(C\) et pour tout l'\(x\)intervalle d'intérêt. Les fonctions qui ne sont pas linéairement dépendantes sont dites linéairement indépendantes.
Déterminez si les paires de fonctions suivantes sont linéairement dépendantes ou linéairement indépendantes.
- \(f_1(x)=x^2\)et\(f_2(x)=5x^2\)
- \(f_1(x)= \sin x\)et\(f_2(x)= \cos x\)
- \(f_1(x)=e^{3x}\)et\(f_2(x)=e^{-3x}\)
- \(f_1(x)=3x\)et\(f_2(x)=3x+1\)
Solution
- \(f_2(x)=5f_1(x),\)les fonctions sont donc linéairement dépendantes.
- Il n'y a pas de constante\(C\)\(f_1(x)=Cf_2(x),\) telle que les fonctions soient linéairement indépendantes.
- Il n'y a pas de constante\(C\)\(f_1(x)=Cf_2(x),\) telle que les fonctions soient linéairement indépendantes. Ne vous laissez pas tromper par le fait que les exposants sont des multiples constants les uns des autres. Avec deux fonctions exponentielles, à moins que les exposants ne soient égaux, les fonctions sont linéairement indépendantes.
- Il n'y a pas de constante\(C\)\(f_1(x)=Cf_2(x),\) telle que les fonctions soient linéairement indépendantes.
Déterminez si les paires de fonctions suivantes sont linéairement dépendantes ou linéairement indépendantes :\(f_1(x)=e^{x}\) et\(f_2(x)=3e^{3x}.\)
- Allusion
-
Les fonctions sont-elles des multiples constants les unes des autres ?
- Réponse
-
Linéairement indépendant
Si nous parvenons à trouver deux solutions linéairement indépendantes à une équation différentielle du second ordre, nous pouvons les combiner pour trouver la solution générale. Ce résultat est formellement énoncé dans le théorème suivant.
Si\(y_1(x)\) et\(y_2(x)\) sont des solutions linéairement indépendantes à une équation différentielle homogène, linéaire et de second ordre, alors la solution générale est donnée par
\[y(x)=c_1y_1(x)+c_2y_2(x), \nonumber \]
où\(c_1\) et\(c_2\) sont des constantes.
Lorsque nous disons qu'une famille de fonctions est la solution générale à une équation différentielle, nous voulons dire que
- chaque expression de cette forme est une solution et
- chaque solution à l'équation différentielle peut être écrite sous cette forme, ce qui rend ce théorème extrêmement puissant.
Si nous pouvons trouver deux solutions linéairement indépendantes à une équation différentielle du second ordre, nous avons effectivement trouvé toutes les solutions à l'équation différentielle du second ordre, ce qui est tout à fait remarquable. La preuve de ce théorème dépasse le cadre de ce texte.
Si\(y_1(t)=e^{3t}\) et\(y_2(t)=e^{-3t}\) existe-t-il des solutions à\(y''-9y=0,\) quelle est la solution générale ?
Solution
Notez que\(y_1\) et ne\(y_2\) sont pas des multiples constants les uns des autres, ils sont donc linéairement indépendants. Ensuite, la solution générale à l'équation différentielle est
\(y(t)=c_1e^{3t}+c_2e^{-3t}.\)
Si\(y_1(x)=e^{3x}\) et\(y_2(x)=xe^{3x}\) existe-t-il des solutions à\(y''-6y'+9y=0,\) quelle est la solution générale ?
- Allusion
-
Vérifiez d'abord l'indépendance linéaire.
- Réponse
-
\(y(x)=c_1e^{3x}+c_2xe^{3x}\)
Équations du second ordre à coefficients constants
Maintenant que nous avons une meilleure idée des équations différentielles linéaires, nous allons nous concentrer sur la résolution d'équations du second ordre de la forme
\[ay''+by'+cy=0, \tag{17.2} \]
où\(a, b,\) et\(c\) sont des constantes.
Comme tous les coefficients sont des constantes, les solutions seront probablement des fonctions dont les dérivées sont des multiples constants d'elles-mêmes. Nous avons besoin de tous les termes à annuler, et si le fait de prendre un dérivé introduit un terme qui n'est pas un multiple constant de la fonction d'origine, il est difficile de voir comment ce terme s'annule. Les fonctions exponentielles ont des dérivées qui sont des multiples constants de la fonction d'origine. Voyons donc ce qui se passe lorsque nous essayons une solution de la forme\(y(x)=e^{ \lambda x}\), où\(\lambda\) (la lettre grecque minuscule lambda) est une constante.
Si\(y(x)=e^{ \lambda x}\), alors\(y'(x)= \lambda e^{ \lambda x}\) et en\(y''= \lambda^2 e^{ \lambda x}.\) substituant ces expressions dans l'équation \ ref {17.1}, nous obtenons
\[\begin{align*} ay''+by'+cy &= a(\lambda^2e^{\lambda x})+b(\lambda e^{\lambda x})+ce^{\lambda x} \\[4pt] &=e^{\lambda x}(a \lambda^2+b \lambda +c). \end{align*}\]
Puisque n'\(e\lambda x\)est jamais nul, cette expression ne peut être égale à zéro pour tous\(x\) que si
\[a\lambda 2+b\lambda +c=0. \nonumber \]
C'est ce que nous appelons l'équation caractéristique de l'équation différentielle.
L'équation caractéristique de l'équation différentielle du second ordre\(ay''+by'+cy=0\) est
\[a\lambda^2+b\lambda +c=0. \nonumber \]
L'équation caractéristique est très importante pour trouver des solutions aux équations différentielles de cette forme. Nous pouvons résoudre l'équation caractéristique soit par factorisation, soit en utilisant la formule quadratique
\[\lambda = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Cela donne trois cas. L'équation caractéristique a
- racines réelles distinctes ;
- une racine réelle unique et répétée ; ou
- racines conjuguées complexes.
Nous examinons chacun de ces cas séparément.
Cas 1 : Des racines réelles distinctes
Si l'équation caractéristique a des racines réelles distinctes\(\lambda_1\) et\(\lambda_2\) que ce\(e^{\lambda_2x}\) sont des solutions linéairement indépendantes de Example \ ref {17.1}, et que la solution générale est donnée par\(e^{\lambda_1x}\)
\[y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}, \nonumber \]
où\(c_1\) et\(c_2\) sont des constantes.
Par exemple, l'équation différentielle\(y''+9y'+14y=0\) a l'équation caractéristique associée.\(\lambda^2+9\lambda+14=0.\) Ce facteur a\((\lambda +2)(\lambda +7)=0,\) des racines\(\lambda_1=-2\) et,\(\lambda_2=-7.\) par conséquent, la solution générale à cette équation différentielle est
\[y(x)=c_1e^{-2x}+c_2e^{-7x}. \nonumber \]
Cas 2 : Racine réelle répétée unique
Les choses sont un peu plus compliquées si l'équation caractéristique a une racine réelle répétée,\(\lambda\). Dans ce cas, nous savons qu'il\(e^{\lambda x}\) s'agit d'une solution à l'équation \ ref {17.1}, mais il ne s'agit que d'une solution et nous avons besoin de deux solutions linéairement indépendantes pour déterminer la solution générale. Nous pourrions être tentés d'essayer une fonction de la forme\(ke^{\lambda x},\) où se\(k\) trouve une constante, mais elle ne serait pas linéairement indépendante de.\(e^{\lambda x}.\) Par conséquent, essayons\(xe^{\lambda x}\) comme deuxième solution. Tout d'abord, notez que selon la formule quadratique,
\[\lambda = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Mais,\(\lambda\) est une racine répétée, donc le discriminate (\(b^2-4ac\)) vaut zéro et\(\lambda = \frac{-b}{2a}\). Ainsi, si\(y=xe^{\lambda x}\), nous avons
\[\begin{align*} y' =e^{\lambda x}+ \lambda xe^{\lambda x} \\[4pt] y'' =2\lambda e^{\lambda x}+\lambda^2xe^{\lambda x}. \end{align*}\]
En substituant les deux expressions dans l'équation \ ref {17.1}, nous voyons que
\[\begin{align*} ay''+by′+cy &=a(2λe^{λx}+λ^2xe^{λx})+b(e^{λx}+λxe^{λx})+cxe^{λx} \\[4pt] &=xe^{λx}(aλ^2+bλ+c)+e^{λx}(2aλ+b) \\[4pt] &=xe^{λx}(0)+e^{λx}(2a(−b2a)+b)\\[4pt] &=0+e^{λx}(0) \\[4pt] &\overset{\checkmark}{=}0. \end{align*}\]
Cela montre qu'il\(xe^{\lambda x}\) s'agit d'une solution à l'équation \ ref {17.1}. Puisque\(e^{\lambda x}\) et\(xe^{\lambda x}\) sont linéairement indépendants, lorsque l'équation caractéristique a une racine répétée\(\lambda \), la solution générale de l'équation \ ref {17.1} est donnée par
\[y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}, \nonumber \]
où\(c_1\) et\(c_2\) sont des constantes.
Par exemple, l'équation différentielle\(y''+12y'+36y=0\) possède l'équation caractéristique associée
\[\lambda^2+12 \lambda +36=0.\nonumber \]
Ce facteur\((\lambda +6)^2=0,\) a une racine répétée\(\lambda =-6\). Par conséquent, la solution générale à cette équation différentielle est
\[y(x)=c_1e^{-6x}+c_2xe^{-6x}.\nonumber \]
Cas 3 : Racines conjuguées complexes
Le troisième cas que nous devons considérer est celui où,\(b^2-4ac <0.\) dans ce cas, lorsque nous appliquons la formule quadratique, nous prenons la racine carrée d'un nombre négatif. Nous devons utiliser le nombre imaginaire\( i= \sqrt{-1}\) pour trouver les racines, qui prennent la forme\(\lambda_1= \alpha + \beta i \) et\(\lambda _2=\alpha -\beta i.\) le nombre complexe\( \alpha +\beta i\) est appelé le conjugué de\( \alpha -\beta i\). Ainsi, nous voyons que lorsque la discrimination\(b^2-4ac\) est négative, les racines de notre équation caractéristique sont toujours des conjugués complexes.
Cela nous pose un petit problème. Si nous suivons le même processus que celui que nous avons utilisé pour des racines réelles distinctes, en utilisant les racines de l'équation caractéristique comme coefficients dans les exposants des fonctions exponentielles, nous obtenons les fonctions\(e^{(\alpha + \beta i)x}\) et\(e^{(\alpha - \beta i)x}\) nos solutions. Cette approche pose toutefois des problèmes. Tout d'abord, ces fonctions prennent des valeurs complexes (imaginaires), et une discussion complète de ces fonctions dépasse le cadre de ce texte. Ensuite, même si nous étions à l'aise avec les fonctions à valeurs complexes, nous n'aborderons pas dans ce cours l'idée d'une dérivée pour de telles fonctions. Donc, si possible, nous aimerions trouver deux solutions de valeur réelle linéairement indépendantes à l'équation différentielle. Pour les besoins de ce développement, nous allons manipuler et différencier les fonctions\(e^{(\alpha + \beta i)x}\),\(e^{(\alpha - \beta i)x}\) comme s'il s'agissait de fonctions à valeur réelle. Pour ces fonctions particulières, cette approche est valide mathématiquement, mais sachez qu'il existe d'autres cas où les fonctions à valeurs complexes ne suivent pas les mêmes règles que les fonctions à valeur réelle. Ceux d'entre vous qui souhaitent une discussion plus approfondie sur les fonctions à valeurs complexes devraient consulter un texte d'analyse complexe.
Sur la base\(\alpha \pm \beta i\) des racines de l'équation caractéristique, les fonctions\(e^{(\alpha + \beta i)x}\) et\(e^{(\alpha - \beta i)x}\) sont des solutions linéairement indépendantes de l'équation différentielle et la solution générale est donnée par
\[y(x)=c_1e^{(\alpha +\beta i)x}+c_2e^{(\alpha - \beta i)x}. \nonumber \]
En utilisant quelques choix intelligents pour\(c_1\) et\(c_2\), et un peu de manipulation algébrique, nous pouvons trouver deux solutions linéaires indépendantes et à valeur réelle à l'équation \ ref {17.1} et exprimer notre solution générale en ces termes.
Nous avons rencontré des fonctions exponentielles avec des exposants complexes plus tôt. L'un des outils clés que nous avons utilisés pour exprimer ces fonctions exponentielles en termes de sinus et de cosinus était la formule d'Euler, qui nous indique que
\[\underbrace{e^{i \theta }= \cos \theta+ i \sin \theta}_{\text{Euler’s formula}} \label{Euler} \]
pour tous les nombres réels\(\theta \).
Pour en revenir à la solution générale, nous avons
\[\begin{align*} y(x) &=c_1e^{( \alpha+ \beta i)x}+c_2e^{(\alpha - \beta i)x} \\[4pt] &=c_1e^{\alpha x}e^{\beta ix}+c_2e^{\alpha x}e^{- \beta ix} \\[4pt] &=e^{\alpha x}(c_1e^{\beta ix}+c_2e^{-\beta ix}).\end{align*}\]
En appliquant la formule d'Euler (équation \ ref {Euler}) avec\(\cos(-x)=\cos x\) les identités,\(\sin(-x)=- \sin x,\) nous obtenons
\[\begin{align} y(x) &=e^{\alpha x}[c_1(\cos \beta x+i \sin \beta x)+c_2(\cos(- \beta x)+i \sin(- \beta x))] \nonumber \\[4pt] &=e^{\alpha x}[(c_1+c_2)\cos \beta x+(c_1-c_2)i \sin \beta x]. \label{E1}\end{align} \]
Maintenant, si nous choisissons\(c_1=c_2= \frac{1}{2},\) le deuxième terme est zéro et nous obtenons
\[y(x)=e^{\alpha x} \cos \beta x \nonumber \]
comme solution en valeur réelle à l'équation \ ref {17.1}. De même, si nous choisissons\(c_1=−\frac{i}{2}\) et\(c_2=\frac{i}{2}\), le premier terme de l'équation \ ref {E1} est zéro et nous obtenons
\[y(x)=e^{\alpha x} \sin \beta x \nonumber \]
comme deuxième solution linéairement indépendante et à valeur réelle pour l'équation \ ref {17.1}.
Sur cette base, nous voyons que si l'équation caractéristique possède des racines conjuguées complexes\(\alpha \pm \beta i,\), la solution générale de l'équation \ ref {17.1} est donnée par
\[\begin{align*} y(x) &=c_1e^{\alpha x} \cos \beta x+c_2e^{\alpha x} \sin \beta x \\[4pt] &=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x),\end{align*}\]
où\(c_1\) et\(c_2\) sont des constantes.
Par exemple, l'équation différentielle\(y''-2y'+5y=0\) a l'équation caractéristique associée.\(\lambda ^2-2 \lambda +5=0.\) Par la formule quadratique, les racines de l'équation caractéristique sont\(1\pm 2i.\) Par conséquent, la solution générale de cette équation différentielle est
\[y(x)=e^{x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Résumé des résultats
Nous pouvons résoudre des équations différentielles homogènes, linéaires et de second ordre à coefficients constants en trouvant les racines de l'équation caractéristique associée. La forme de la solution générale varie selon que l'équation caractéristique comporte des racines réelles distinctes, une racine réelle unique et répétée ou des racines conjuguées complexes. Les trois cas sont résumés dans le tableau\(\PageIndex{1}\).
| Racines d'équation caractéristiques | Solution générale à l'équation différentielle |
|---|---|
| De vraies racines distinctes,\(\lambda_1\) et\(\lambda_2\) | \(y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}\) |
| Une vraie racine répétée,\(\lambda \) | \(y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}\) |
| Racines conjuguées complexes\(\alpha \pm \beta i\) | \(y(x)=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x)\) |
- Écrivez l'équation différentielle dans le formulaire\(a''+by'+cy=0.\)
- Trouvez l'équation caractéristique correspondante\(a\lambda^2+b\lambda +c=0.\)
- Facturez l'équation caractéristique ou utilisez la formule quadratique pour trouver les racines.
- Déterminez la forme de la solution générale selon que l'équation caractéristique possède des racines réelles distinctes, une racine réelle unique et répétée ou des racines conjuguées complexes.
Trouvez la solution générale aux équations différentielles suivantes. Donnez vos réponses en fonction de\(x\).
- \(y''+3y'-4y=0\)
- \(y''+6y'+13y=0\)
- \(y''+2y'+y=0\)
- \(y''-5y'=0\)
- \(y''-16y=0\)
- \(y''+16y=0\)
Solution
Notez que toutes ces équations sont déjà données sous forme standard (étape 1).
- L'équation caractéristique est\(\lambda^2+3\lambda -4=0\) (étape 2). Cela prend en compte\((\lambda +4)(\lambda -1)=0\), de sorte que les racines de l'équation caractéristique sont\(\lambda_1=-4\) et\(\lambda_2=1\) (étape 3). La solution générale à l'équation différentielle est alors
\[y(x)=c_1e^{-4x}+c_2e^{x}. \tag{step 1} \]
- L'équation caractéristique est\(\lambda^2+6\lambda+13=0\) (étape 2). En appliquant la formule quadratique, nous voyons que cette équation a des racines conjuguées complexes\(-3\pm 2i\) (étape 3). La solution générale à l'équation différentielle est alors
\[y(t)=e^{-3t}(c_1 \cos 2t+c_2 \sin 2t). \tag{step 2} \]
- L'équation caractéristique est\(\lambda^2+2\lambda+1=0\) (étape 2). Cela permet de\((\lambda+1)2=0,\) faire en sorte que l'équation caractéristique ait une racine réelle répétée\(\lambda =-1\) (étape 3). La solution générale à l'équation différentielle est alors
\[y(t)=c_1e^{-t}+c_2te^{-t}. \tag{step 3} \]
- L'équation caractéristique est\(\lambda^2-5\lambda\) (étape 2). Cela explique\(\lambda(\lambda -5)=0,\) que les racines de l'équation caractéristique sont\(\lambda_1=0\) et\(\lambda_2=5\) (étape 3). Notez que\(e^{0x}=e^{0}=1\) notre première solution n'est donc qu'une constante. La solution générale à l'équation différentielle est alors
\[y(x)=c_1+c_2e^{5x}. \tag{step 4} \]
- L'équation caractéristique est\(\lambda^2-16=0\) (étape 2). Cela explique\((\lambda+4)(\lambda -4)=0,\) que les racines de l'équation caractéristique sont\(\lambda_1=4\) et\(\lambda_2=-4\) (étape 3). La solution générale à l'équation différentielle est alors
\[y(x)=c_1e^{4x}+c_2e^{-4x}. \tag{step 5} \]
- L'équation caractéristique est\(\lambda^2+16=0\) (étape 2). Il possède des racines conjuguées complexes\(\pm 4i\) (étape 3). Notez que\(e^{0x}=e^0=1\) le terme exponentiel dans notre solution n'est donc qu'une constante. La solution générale à l'équation différentielle est alors
\[y(t)=c_1 \cos 4t+c_2 \sin 4t. \tag{step 6} \]
Trouvez la solution générale aux équations différentielles suivantes :
- \(y''-2y'+10y=0\)
- \(y''+14y'+49y=0\)
- Allusion
-
Trouvez les racines de l'équation caractéristique.
- Répondez à une
-
\(y(x)=e^x(c_1 \cos 3x+c_2 \sin 3x)\)
- Réponse b
-
\(y(x)=c_1e^{-7x}+c_2xe^{-7x}\)
Problèmes de valeur initiale et problèmes de valeurs limites
Jusqu'à présent, nous avons trouvé des solutions générales aux équations différentielles. Cependant, les équations différentielles sont souvent utilisées pour décrire des systèmes physiques, et la personne qui étudie ce système physique sait généralement quelque chose sur l'état de ce système à un ou plusieurs moments dans le temps. Par exemple, si une équation différentielle à coefficient constant représente la distance de compression d'un amortisseur de moto, nous pouvons savoir que le pilote est immobile sur sa moto au début d'une course.\(t=t_0.\) Cela signifie que le système est en équilibre, donc\(y(t_0)=0,\) et la compression de l'amortisseur ne change pas, donc\(y'(t_0)=0.\) avec ces deux conditions initiales et la solution générale de l'équation différentielle, nous pouvons trouver la solution spécifique à l'équation différentielle qui satisfait les deux conditions initiales. Ce processus est connu sous le nom de résolution d'un problème de valeur initiale. (Rappelons que nous avons discuté des problèmes liés aux valeurs initiales dans Introduction aux équations différentielles.) Notez que les équations du second ordre ont deux constantes arbitraires dans la solution générale et que, par conséquent, nous avons besoin de deux conditions initiales pour trouver la solution au problème de valeur initiale.
Parfois, nous connaissons l'état du système à deux moments différents. Par exemple, nous pouvons connaître\(y(t_0)=y_0\) et\(y(t_1)=y_1.\) ces conditions sont appelées conditions limites, et trouver la solution à l'équation différentielle qui satisfait les conditions limites s'appelle résoudre un problème de valeur limite.
Les mathématiciens, les scientifiques et les ingénieurs souhaitent comprendre les conditions dans lesquelles un problème de valeur initiale ou un problème de valeurs limites a une solution unique. Bien qu'un traitement complet de ce sujet dépasse le cadre de ce texte, il est utile de savoir que, dans le contexte d'équations de second ordre à coefficient constant, les problèmes de valeur initiale ont la garantie d'avoir une solution unique tant que deux conditions initiales sont remplies. Les problèmes liés aux valeurs limites ne sont toutefois pas aussi bien gérés. Même lorsque deux conditions limites sont connues, nous pouvons rencontrer des problèmes de valeurs limites avec des solutions uniques, de nombreuses solutions ou aucune solution du tout.
Résolvez le problème de valeur initiale suivant :\(y''+3y'-4y=0, \, y(0)=1,\, y'(0)=-9.\)
Solution
Nous avons déjà résolu cette équation différentielle dans l'exemple 17.6a. et avons trouvé la solution générale
\[y(x)=c_1e^{-4x}+c_2e^{x}. \nonumber \]
Alors
\[y'(x)=-4c_1e^{-4x}+c_2e^{x}. \nonumber \]
Lorsque\(x=0,\) nous avons\(y(0)=c_1+c_2\) et\(y'(0)=-4c_1+c_2.\) en appliquant les conditions initiales, nous avons
\[\begin{align*} c_1+c_2 &=1 \\[4pt] -4c_1+c_2 &=-9.\end{align*}\]
Ensuite, en\(c_1=1-c_2.\) substituant cette expression dans la deuxième équation, nous voyons que
\[\begin{align*} -4(1-c_2)+c_2 &= -9 \\[4pt] -4+4c_2+c_2 &=-9 \\[4pt] 5c_2 &=-5 \\[4pt] c_2 &=-1. \end{align*}\]
Donc,\(c_1=2\) et la solution au problème de la valeur initiale est
\[y(x)=2e^{-4x}-e^{x}. \nonumber \]
Résolvez le problème de la valeur initiale\(y''-3y'-10y=0, \quad y(0)=0, \; y'(0)=7.\)
- Allusion
-
Utilisez les conditions initiales pour déterminer les valeurs pour\(c_1\) et\(c_2\).
- Réponse
-
\[y(x)=-e^{-2x}+e^{5x} \nonumber \]
Résolvez le problème de valeur initiale suivant et représentez la solution sous forme graphique :
\[y''+6y'+13y=0, \quad y(0)=0, \; y'(0)=2\nonumber \]
Solution
Nous avons déjà résolu cette équation différentielle dans Example\(\PageIndex{6b}\). Et nous avons trouvé la solution générale
\[y(x)=e^{-3x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Alors
\[y'(x)=e^{-3x}(-2c_1 \sin 2x+2c_2 \cos 2x)-3e^{-3x}(c_1 \cos 2x+c_2 \sin 2x). \nonumber \]
Quand\(x=0,\) nous avons\(y(0)=c_1\) et\(y'(0)=2c_2-3c_1\). En appliquant les conditions initiales, nous obtenons
\[ \begin{align*} c_1 &=0 \\[4pt] -3c_1+2c_2 &=2. \end{align*}\]
Par conséquent,\(c_1=0, \, c_2=1,\) la solution au problème de valeur initiale est présentée dans le graphique suivant.
\[y=e^{-3x} \sin 2x.\nonumber \]
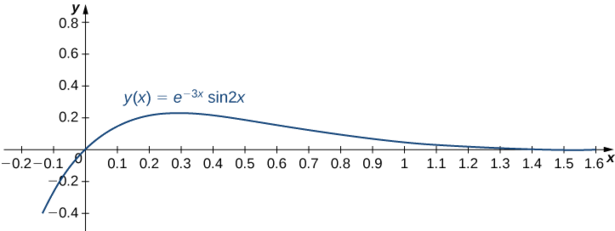
Résolvez le problème de valeur initiale suivant et représentez la solution sous forme graphique :\(y''-2y'+10y=0, \quad y(0)=2, \; y'(0)=-1\)
- Allusion
-
Utilisez les conditions initiales pour déterminer les valeurs pour\(c_1\) et\(c_2.\)
- Réponse
-
\[y(x)=e^{x}(2 \cos 3x - \sin 3x) \nonumber \]
Le problème de valeur initiale suivant modélise la position d'un objet dont la masse est attachée à un ressort. Les systèmes à masse à ressort sont examinés en détail dans Applications. La solution de l'équation différentielle donne la position de la masse par rapport à une position neutre (d'équilibre) (en mètres) à tout moment donné. (Notez que pour les systèmes à masse à ressort de ce type, il est habituel de définir la direction vers le bas comme positive.)
\[y''+2y'+y=0, \quad y(0)=1, \; y'(0)=0 \nonumber \]
Résolvez le problème de valeur initiale et représentez la solution sous forme graphique. Quelle est la position de la masse au temps\(t=2\) sec ? À quelle vitesse la masse se déplace-t-elle en une\(t=1\) seconde ? Dans quelle direction ?
Solution
Dans l'exemple Exemple\(\PageIndex{6c}\)... nous avons trouvé que la solution générale à cette équation différentielle était
\[y(t)=c_1e^{-t}+c_2te^{-t}. \nonumber \]
Alors
\[y'(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t}). \nonumber \]
Lorsque\(t=0,\) nous avons\(y(0)=c_1\) et\(y'(0)=c_1+c_2.\) en appliquant les conditions initiales, nous obtenons
\[c_1=1 \\ -c_1+c_2=0. \nonumber \]
Ainsi,\(c_1=1, c_2=1,\) et la solution au problème de valeur initiale est
\[y(t)=e^{-t}+te^{-t}. \nonumber \]
Cette solution est représentée dans le graphique suivant. À ce moment\(t=2,\), la masse se trouve en position\(y(2)=e^{-2}+2e^{-2}=3e^{-2} \approx 0.406\) m en dessous de l'équilibre.
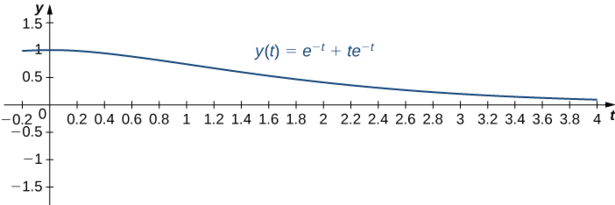
Pour calculer la vitesse dans le temps,\(t=1,\) nous devons trouver la dérivée. Nous l'avons\(y(t)=e^{-t}+te^{-t},\) donc
\[y'(t)=-e^{-t}+e^{-t}-te^{-t}= -te^{-t}. \nonumber \]
Alors\(y'(1)=-e^{-1} \approx -0.3679\). À un moment\(t=1,\), la masse se déplace vers le haut à\(0.3679\) m/sec.
Supposons que le problème de valeur initiale suivant modélise la position (en pieds) d'une masse dans un système masse-ressort à un moment donné. Résolvez le problème de valeur initiale et représentez la solution sous forme graphique. Quelle est la position de la masse au temps\(t=0.3\) sec ? À quelle vitesse se déplace-t-il en une\(t=0.1\) seconde ? Dans quelle direction ?
\[y''+14y'+49y=0, \quad y(0)=0, \; y'(0)=1 \nonumber \]
- Allusion
-
Utilisez les conditions initiales pour déterminer les valeurs pour\(c_1\) et\(c_2\).
- Réponse
-
\[y(t)=te^{-7t}\nonumber \]
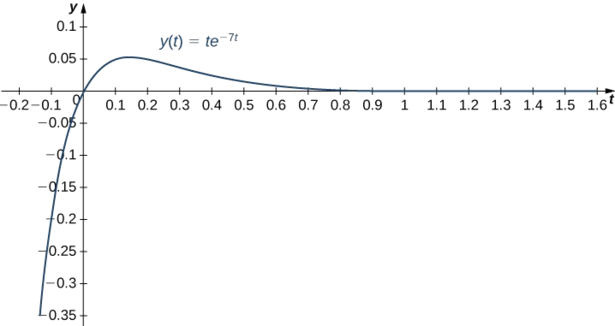
Au moment où\(t=0.3, \; y(0.3)=0.3e^{(-7^{\ast} 0.3)}=0.3e^{-2.1} \approx 0.0367. \) la masse est\(0.0367\) inférieure à l'équilibre. À\(t=0.1, \; y'(0.1)=0.3e^{-0.7} \approx 0.1490.\) l'heure La masse se déplace vers le bas à une vitesse de\(0.1490\) pieds par seconde.
Dans l'exemple 17.6f, nous avons résolu l'équation différentielle\(y''+16y=0\) et avons trouvé la solution générale suivante :\(y(t)=c_1 \cos 4t+c_2 \sin 4t.\) si possible, résolvez le problème des valeurs limites si les conditions aux limites sont les suivantes :
- \(y(0)=0, y( \frac{\pi}{4})=0\)
- \(y(0)=1,y(0)=1, y(\frac{\pi}{8})=0\)
- \(y(\frac{\pi}{8})=0, y(\frac{3 \pi}{8})=2\)
Solution
Nous avons
\[y(x)=c_1 \cos 4t+c_2 \sin 4t. \nonumber \]
- En appliquant la première condition limite donnée ici, nous obtenons\(y(0)=c_1=0.\) Donc, la solution est de la forme\(y(t)=c_2 \sin 4t.\) Lorsque nous appliquons la deuxième condition limite, nous obtenons\(y(\frac{\pi}{4})=c_2 \sin(4(\frac{\pi}{4}))=c_2 \sin \pi =0 \) pour toutes les valeurs de\(c_2\). Les conditions limites ne sont pas suffisantes pour déterminer une valeur, de\(c_2,\) sorte que ce problème de valeur limite a une infinité de solutions. Ainsi,\(y(t)=c_2 \sin 4t\) est une solution pour n'importe quelle valeur de\(c_2\).
- En appliquant la première condition limite donnée ici, nous obtenons L'\(y(0)=c_1=1.\)application de la deuxième condition limite donne\(y(\frac{\pi}{8})=c_2=0,\) ainsi\(c_2=0.\) Dans ce cas, nous avons une solution unique :\(y(t)= \cos 4t\).
- En appliquant la première condition limite donnée ici, nous obtenons\(y(\frac{\pi}{8})=c_2=0.\) Cependant, l'application de la deuxième condition limite donne\(y(\frac{3 \pi}{8})=-c_2=2,\) donc\(c_2=-2.\) Nous ne pouvons pas avoir,\(c_2=0=-2,\) donc ce problème de valeur limite n'a pas de solution.
Concepts clés
- Les équations différentielles du second ordre peuvent être classées comme linéaires ou non linéaires, homogènes ou non homogènes.
- Pour trouver une solution générale à une équation différentielle homogène du second ordre, nous devons trouver deux solutions linéairement indépendantes. Si\(y_1(x)\) et\(y_2(x)\) sont des solutions linéairement indépendantes à une équation différentielle homogène, linéaire et de second ordre, alors la solution générale est donnée par
\[y(x)=c_1y_1(x)+c_2y_2(x).\nonumber \]
- Pour résoudre des équations différentielles homogènes du second ordre à coefficients constants, trouvez les racines de l'équation caractéristique. La forme de la solution générale varie selon que l'équation caractéristique comporte des racines réelles distinctes, une racine réelle unique et répétée ou des racines conjuguées complexes.
- Les conditions initiales ou les conditions limites peuvent ensuite être utilisées pour trouver la solution spécifique à une équation différentielle qui satisfait ces conditions, sauf en cas d'absence de solution ou d'un nombre infini de solutions.
Équations clés
- Équation différentielle linéaire du second\[a_2(x)y''+a_1(x)y'+a_0(x)y=r(x) \nonumber \]
- Équation du second ordre à coefficients constants\[ay''+by'+cy=0 \nonumber \]
Lexique
- conditions limites
- les conditions qui donnent l'état d'un système à différents moments, telles que la position d'un système masse-ressort à deux moments différents
- problème de valeur limite
- une équation différentielle avec les conditions limites associées
- équation caractéristique
- l'équation\(aλ^2+bλ+c=0\) de l'équation différentielle\(ay″+by′+cy=0\)
- équation linéaire homogène
- une équation différentielle du second ordre qui peut être écrite sous la forme\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), mais\(r(x)=0\) pour chaque valeur de\(x\)
- équation linéaire non homogène
- une équation différentielle du second ordre qui peut être écrite sous la forme\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), mais\(r(x)≠0\) pour une certaine valeur de\(x\)
- dépendant linéairement
- un ensemble de fonctions\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) pour lesquelles il existe des constantes\(c_1,\,c_2,\,…,\,c_n\), pas toutes nulles, de telle sorte que\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) pour toutes les fonctions\(x\) comprises dans l'intervalle d'intérêt
- linéairement indépendant
- un ensemble de fonctions\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) pour lesquelles il n'y a pas de constantes\(c_1,\,c_2,\,…,\,c_n\), de telle sorte que\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) pour toutes les fonctions\(x\) comprises dans l'intervalle d'intérêt


