16.7E : Exercices pour la section 16.7

Last updated
Save as PDF

Page ID: 197877

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 6, sans utiliser le théorème de Stokes, calculez directement à la fois le flux de$curl \, \vecs F \cdot \vecs N$ sur la surface donnée et l'intégrale de circulation autour de sa limite, en supposant que toutes sont orientées dans le sens des aiguilles d'une montre.

1. $\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + z^2\,\mathbf{\hat j} + x^2\,\mathbf{\hat k}$;$S$ est la première partie octante du plan$x + y + z = 1$.

2. $\vecs F(x,y,z) = z\,\mathbf{\hat i} + x\,\mathbf{\hat j} + y\,\mathbf{\hat k}$;$S$ est un hémisphère$z = (a^2 - x^2 - y^2)^{1/2}$.

Réponse: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = \pi a^2$

3. $\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 5\,\mathbf{\hat k}$;$S$ est un hémisphère$z = (4 - x^2 - y^2)^{1/2}$.

4. $\vecs F(x,y,z) = z\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 3y\,\mathbf{\hat k}$;$S$ est l'hémisphère supérieur$z = \sqrt{9 - x^2 - y^2}$.

Réponse: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 18 \pi$

5. $\vecs F(x,y,z) = (x + 2z)\,\mathbf{\hat i} + (y - x)\,\mathbf{\hat j} + (z - y)\,\mathbf{\hat k}$;$S$ est une région triangulaire avec des sommets$(3, 0, 0), \, (0, 3/2, 0),$ et$(0, 0, 3).$

6. $\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + 6z\,\mathbf{\hat j} + 3x\,\mathbf{\hat k}$;$S$ est une partie du paraboloïde$z = 4 - x^2 - y^2$ située au-dessus du$xy$ plan.

Réponse: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = -8 \pi$

Dans les exercices 7 à 9, utilisez le théorème de Stokes$\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS$ pour évaluer les champs vectoriels et la surface.

7. $\vecs F(x,y,z) = xy\,\mathbf{\hat i} - z\,\mathbf{\hat j}$et$S$ est la surface du cube$0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$, à l'exception de la face où$z = 0$ et en utilisant le vecteur normal de l'unité extérieure.

8. $\vecs F(x,y,z) = xy\,\mathbf{\hat i} + x^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}$; et$C$ est l'intersection du paraboloïde$z = x^2 + y^2$ et du plan$z = y$, et utilise le vecteur normal vers l'extérieur.

Réponse: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 0$

9. $\vecs F(x,y,z) = 4y\,\mathbf{\hat i} + z \,\mathbf{\hat j} + 2y \,\mathbf{\hat k}$; et$C$ est l'intersection de la sphère$x^2 + y^2 + z^2 = 4$ avec le plan$z = 0$, et en utilisant le vecteur normal vers l'extérieur.

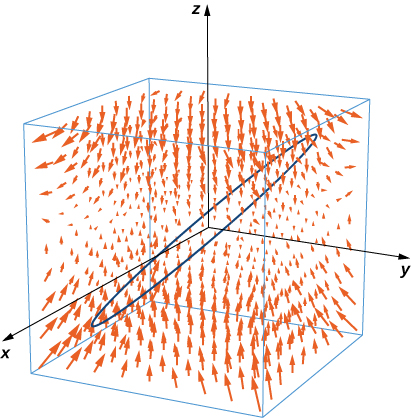
10. Utilisez le théorème de Stokes pour évaluer$\displaystyle \int_C \big[2xy^2z \, dx + 2x^2yz \, dy + (x^2y^2 - 2z) \, dz\big],$ où$C$ se trouve la courbe donnée par$x = \cos t, \, y = \sin t, \, 0 \leq t \leq 2\pi$, parcourue dans le sens de l'augmentation$t.$

$Un champ vectoriel dans un espace tridimensionnel. Les flèches sont d'autant plus grandes qu'elles s'éloignent du plan x, y. Les flèches se courbent vers le haut à partir du dessous du plan x, y et légèrement au-dessus de celui-ci. Les autres ont tendance à se courber vers le bas et horizontalement Une courbe de forme ovale est tracée au milieu de l'espace.$

Réponse: $\displaystyle \int_C \vecs F \cdot dS = 0$

11. [T] Use a computer algebraic system (CAS) and Stokes’ theorem to approximate line integral $\displaystyle \int_C (y \, dx + z \, dy + x \, dz),$ where $C$ is the intersection of plane $x + y = 2$ and surface $x^2 + y^2 + z^2 = 2(x + y)$, traversed counterclockwise viewed from the origin.

12. [T] Use a CAS and Stokes’ theorem to approximate line integral $\displaystyle \int_C (3y\, dx + 2z \, dy - 5x \, dz),$ where $C$ is the intersection of the $xy$-plane and hemisphere $z = \sqrt{1 - x^2 - y^2}$, traversed counterclockwise viewed from the top—that is, from the positive $z$-axis toward the $xy$-plane.

Answer: $\displaystyle \int_C \vecs F \cdot dS = - 9.4248$

13. [T] Use a CAS and Stokes’ theorem to approximate line integral $\displaystyle \int_C [(1 + y) \, z \, dx + (1 + z) x \, dy + (1 + x) y \, dz],$ where $C$ is a triangle with vertices $(1,0,0), \, (0,1,0)$, and $(0,0,1)$ oriented counterclockwise.

14. Use Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = e^{xy} cos \, z\,\mathbf{\hat i} + x^2 z\,\mathbf{\hat j} + xy\,\mathbf{\hat k}$, and $S$ is half of sphere $x = \sqrt{1 - y^2 - z^2}$, oriented out toward the positive $x$-axis.

Answer: $\displaystyle \iint_S \vecs F \cdot dS = 0$

15. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS,$ where $\vecs F(x,y,z) = x^2 y\,\mathbf{\hat i} + xy^2 \,\mathbf{\hat j} + z^3 \,\mathbf{\hat k}$ and $C$ is the curve of the intersection of plane $3x + 2y + z = 6$ and cylinder $x^2 + y^2 = 4$, oriented clockwise when viewed from above.

16. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = \left( \sin(y + z) - yx^2 - \dfrac{y^3}{3}\right)\,\mathbf{\hat i} + x \, \cos (y + z) \,\mathbf{\hat j} + \cos (2y) \,\mathbf{\hat k}$ and $S$ consists of the top and the four sides but not the bottom of the cube with vertices $(\pm 1, \, \pm1, \, \pm1)$, oriented outward.

Answer: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 2.6667$

17. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + 3xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}$ and $S$ is the top part of $z = 5 - x^2 - y^2$ above plane $z = 1$ and $S$ is oriented upward.

18. Use Stokes’ theorem to evaluate $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,$ where $\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + x\,\mathbf{\hat k}$ and $S$ is a triangle with vertices $(1, 0, 0), \, (0, 1, 0)$ and $(0, 0, 1)$ with counterclockwise orientation.

Answer: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -\dfrac{1}{6}$

19. Use Stokes’ theorem to evaluate line integral $\displaystyle \int_C (z \, dx + x \, dy + y \, dz),$ where $C$ is a triangle with vertices $(3, 0, 0), \, (0, 0, 2),$ and $(0, 6, 0)$ traversed in the given order.

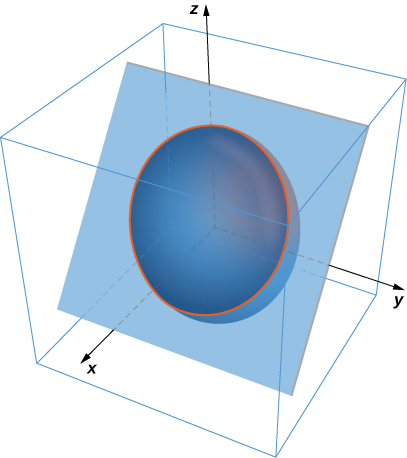
20. Use Stokes’ theorem to evaluate $\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right),$ where $C$ is the curve of intersection of plane $x + z = 1$ and ellipsoid $x^2 + 2y^2 + z^2 = 1$, oriented clockwise from the origin.

$A diagram of an intersecting plane and ellipsoid in three dimensional space. There is an orange curve drawn to show the intersection.$

Réponse: $\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right) = - \dfrac{\pi}{4}$

21. Utilisez le théorème de Stokes pour évaluer$\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,$ où$\vecs F(x,y,z) = x\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + ze^{xy}\,\mathbf{\hat k}$ et$S$ se trouve la partie de la surface$z = 1 - x^2 - 2y^2$$z \geq 0$, orientée dans le sens antihoraire.

22. Utilisez le théorème de Stokes pour un champ vectoriel$\vecs F(x,y,z) = z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 2z\,\mathbf{\hat k}$ où$S$$C$ est une surface$z = 1 - x^2 - 2y^2, \, z \geq 0$$x^2 + y^2 = 1$, un cercle limite et$S$ est orienté dans la$z$ direction positive.

Réponse: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -3\pi$

23. Utilisez le théorème de Stokes pour le champ vectoriel$\vecs F(x,y,z) = - \dfrac{3}{2} y^2\,\mathbf{\hat i} - 2 xy\,\mathbf{\hat j} + yz\,\mathbf{\hat k}$, où$S$ est la partie de la surface du plan$x + y + z = 1$ contenue dans un triangle$C$ avec des sommets$(1, 0, 0), \, (0, 1, 0),$ et$(0, 0, 1),$ parcourue dans le sens antihoraire vu de dessus.

24. Une certaine trajectoire fermée$C$ dans le plan$2x + 2y + z = 1$ est connue pour se projeter sur un cercle unitaire$x^2 + y^2 = 1$ dans le$xy$ plan. $C$Soyons une constante et laissez$\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}$. Utilisez le théorème de Stokes pour évaluer$\displaystyle \int_C(c \,\mathbf{\hat k} \times \vecs R) \cdot dS.$

Réponse: $\displaystyle \int_C (c \,\mathbf{\hat k} \times \vecs R) \cdot dS = 2\pi c$

25. Utilisez le théorème de Stokes et laissez$C$ être la limite de la surface$z = x^2 + y^2$ avec la normale$0 \leq y \leq 1$ orientée vers le haut$0 \leq x \leq 2$ et orientée vers le haut. Définissez$\vecs F(x,y,z) = \big(\sin (x^3) + xz\big) \,\mathbf{\hat i} + (x - yz)\,\mathbf{\hat j} + \cos (z^4) \,\mathbf{\hat k}$ et évaluez$\int_C \vecs F \cdot dS$.

26. $S$Soit un hémisphère$x^2 + y^2 + z^2 = 4$ avec$z \geq 0$, orienté vers le haut. $\vecs F(x,y,z) = x^2 e^{yz}\,\mathbf{\hat i} + y^2 e^{xz} \,\mathbf{\hat j} + z^2 e^{xy}\,\mathbf{\hat k}$Soit un champ vectoriel. Utilisez le théorème de Stokes pour évaluer$\displaystyle \iint_S curl \, \vecs F \cdot dS.$

Réponse: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 0$

27. Soit$\vecs F(x,y,z) = xy\,\mathbf{\hat i} + (e^{z^2} + y)\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}$ et$S$ soit le graphe de la fonction$z \leq 0$ orienté$y = \dfrac{x^2}{9} + \dfrac{z^2}{9} - 1$ de telle sorte que le vecteur normal$S$ ait une composante y positive. Utiliser le théorème de Stokes pour calculer l'intégrale$\displaystyle \iint_S curl \, \vecs F \cdot dS.$

28. Utilisez le théorème de Stokes pour évaluer$\displaystyle \oint \vecs F \cdot dS,$ où$\vecs F(x,y,z) = y\,\mathbf{\hat i} + z\,\mathbf{\hat j} + x\,\mathbf{\hat k}$ et$C$ se trouve un triangle avec des sommets$(0, 0, 0), \, (2, 0, 0)$ et$0,-2,2)$ orienté dans le sens antihoraire vu de dessus.

Réponse: $\displaystyle \oint \vecs F \cdot dS = -4$

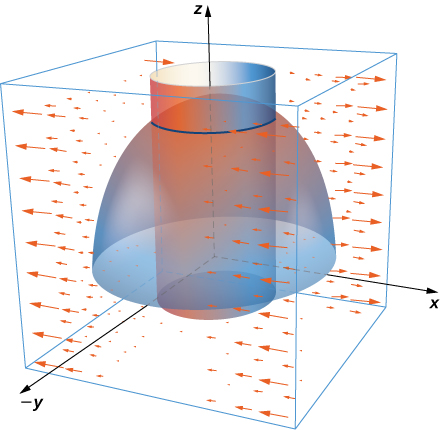
29. Utilisez l'intégrale de surface du théorème de Stokes pour calculer la circulation du champ$\vecs F,$$\vecs F(x,y,z) = x^2y^3 \,\mathbf{\hat i} + \,\mathbf{\hat j} + z\,\mathbf{\hat k}$ autour$C,$ duquel se trouve l'intersection du cylindre$x^2 + y^2 = 4$ et de l'hémisphère$x^2 + y^2 + z^2 = 16, \, z \geq 0$, orientée dans le sens antihoraire vu de dessus.

$Schéma en trois dimensions d'un champ vectoriel et de l'intersection d'une sylinder et d'un hémisphère. Les flèches sont horizontales et comportent des composantes x négatives pour les composantes y négatives et des composantes x positives pour les composantes y positives. La courbe d'intersection entre l'hémisphère et le cylindre est dessinée en bleu.$

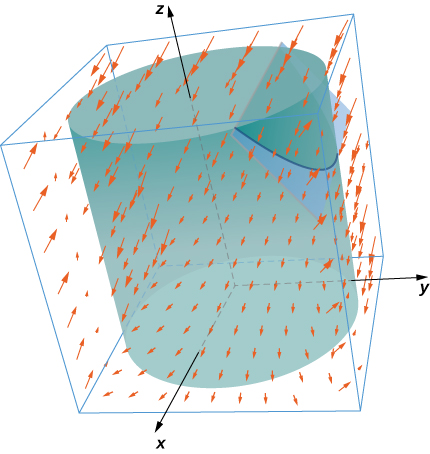
30. Utilisez le théorème de Stokes pour calculer$\displaystyle \iint_S curl \, \vecs F \cdot dS.$ where $\vecs F(x,y,z) = \,\mathbf{\hat i} + xy^2\,\mathbf{\hat j} + xy^2 \,\mathbf{\hat k}$ and $S$ is a part of plane $y + z = 2$ inside cylinder $x^2 + y^2 = 1$ and oriented counterclockwise.

$A diagram of a vector field in three dimensional space showing the intersection of a plane and a cylinder. The curve where the plane and cylinder intersect is drawn in blue.$

Réponse: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 0$

31. Utilisez le théorème de Stokes pour évaluer$\displaystyle \iint_S curl \, \vecs F \cdot dS,$ où$\vecs F(x,y,z) = -y^2 \,\mathbf{\hat i} + x\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}$ et$S$ est la partie du plan$x + y + z = 1$ dans l'octant positif et orientée dans le sens antihoraire$x \geq 0, \, y \geq 0, \, z \geq 0$.

32. $C$Soit$\vecs F(x,y,z) = xy\,\mathbf{\hat i} + 2z\,\mathbf{\hat j} - 2y\,\mathbf{\hat k}$ l'intersection du plan$x + z = 5$ et du cylindre$x^2 + y^2 = 9$, qui est orientée dans le sens antihoraire lorsqu'on la regarde depuis le haut. Calculez l'intégrale linéaire de$\vecs F$ over$C$ à l'aide du théorème de Stokes.

Réponse: $\displaystyle \iint_S curl \, \vecs F \cdot dS = -36 \pi$

33. [T] Utilisez un CAS et laissez$\vecs F(x,y,z) = xy^2\,\mathbf{\hat i} + (yz - x)\,\mathbf{\hat j} + e^{yxz}\,\mathbf{\hat k}$. Utilisez le théorème de Stokes pour calculer l'intégrale de surface de la courbure$\vecs F$ sur$S$ une surface orientée vers l'intérieur constituée d'un cube$[0,1] \times [0,1] \times [0,1]$ dont le côté droit est absent.

34. $S$Soit un ellipsoïde$\dfrac{x^2}{4} + \dfrac{y^2}{9} + z^2 = 1$ orienté dans le sens antihoraire et$\vecs F$ soit un champ vectoriel avec des fonctions constitutives qui ont des dérivées partielles continues.

Réponse: $\displaystyle \iint_S curl \, \vecs F \cdot \vecs N = 0$

35. Que$S$ vous fassiez partie du paraboloïde$z = 9 - x^2 - y^2$ avec$z \geq 0$. Vérifiez le théorème de Stokes pour le champ vectoriel$\vecs F(x,y,z) = 3z\,\mathbf{\hat i} + 4x\,\mathbf{\hat j} + 2y\,\mathbf{\hat k}$.

36. [T] Utilisez un CAS et le théorème de Stokes pour évaluer$\displaystyle \oint \vecs F \cdot dS,$ si$\vecs F(x,y,z) = (3z - \sin x) \,\mathbf{\hat i} + (x^2 + e^y) \,\mathbf{\hat j} + (y^3 - \cos z) \,\mathbf{\hat k}$ et où$C$ est la courbe donnée par$x = \cos t, \, y = \sin t, \, z = 1; \, 0 \leq t \leq 2\pi$.

Réponse: $\displaystyle \oint_C \vecs F \cdot d\vecs{r} = 0$

37. [T] Utilisez un CAS et le théorème de Stokes pour évaluer$\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + e^z\,\mathbf{\hat j} - \arctan x \,\mathbf{\hat k}$ avec$S$ une portion de paraboloïde$z = 4 - x^2 - y^2$ coupée par le$xy$ plan orienté dans le sens antihoraire.

38. [T] Utilisez un CAS pour évaluer la$\displaystyle \iint_S curl (F) \cdot dS,$ position$\vecs F(x,y,z) = 2z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 5y\,\mathbf{\hat k}$ et la$S$ position de la surface de manière paramétrique$\vecs r(r,\theta) = r \, \cos \theta \,\mathbf{\hat i} + r \, \sin \theta \,\mathbf{\hat j} + (4 - r^2) \,\mathbf{\hat k} \, (0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 3)$.

Réponse: $\displaystyle \iint_S curl (F) \cdot dS = 84.8230$

39. $S$Soyons paraboloïdes$z = a (1 - x^2 - y^2)$$z \geq 0$, car où se$a > 0$ trouve un vrai nombre. Laissez$\vecs F(x,y,z) = \langle x - y, \, y + z, \, z - x \rangle$. Pour quelle (s) valeur (s) de$a$ (le cas échéant)$\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS$ a sa valeur maximale ?

Pour les exercices d'application 40 à 41, l'objectif est d'évaluer$\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS,$ où$\vecs F = \langle xz, \, -xz, \, xy \rangle$ et$S$ se trouve la moitié supérieure de l'ellipsoïde$x^2 + y^2 + 8z^2 = 1$, où$z \geq 0$.

40. Évaluez une intégrale de surface sur une surface plus pratique pour trouver la valeur de$A.$

Réponse: $\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS = 0$

41. Évaluez$A$ à l'aide d'une intégrale linéaire.

42. Prenez du paraboloïde$z = x^2 + y^2$, formez$0 \leq z \leq 4$, et tranchez-le avec de l'avion$y = 0$. $S$Soit la surface qui reste pour$y \geq 0$, y compris la surface plane dans le$xz$ plan. $C$Soit le demi-cercle et le segment de ligne qui délimitaient le sommet d'un plan$z = 4$ orienté$S$ dans le sens antihoraire. Laissez$\vecs F = \langle 2z + y, \, 2x + z, \, 2y + x \rangle$. Évaluer$\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS.$

$Schéma d'un champ vectoriel dans un espace tridimensionnel où se croisent un paraboloïde avec un sommet à l'origine, un plan à y=0 et un plan à z=4. La surface restante est la moitié d'un paraboloïde sous z=4 et au-dessus de y=0.$

Réponse: Template:ContribOpenStaxCalc