Skip to main content
Global

15.3E : Exercices pour la section 15.3

  1. Last updated
  2. Save as PDF
  • Page ID
    197502

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Termes et concepts

    1. Lors de\(\displaystyle \int\int_R f(x,y)\,dA\) l'évaluation à l'aide de coordonnées polaires,\(f(x,y)\) est remplacé par _______ et\(dA\) est remplacé par _______.

    Réponse
    \(f(x,y)\)est remplacé par \(f(r\cos \theta, r\sin\theta)\)et\(dA\) est remplacé par \(r\,dr\,d\theta\).

    2. Pourquoi serait-on intéressé à évaluer une double intégrale avec des coordonnées polaires ?

    Définition des régions polaires

    Dans les exercices 3 à 6, exprimez la région\(R\) en coordonnées polaires.

    3)\(R\) est la région du disque de rayon 2 centrée à l'origine qui se trouve dans le premier quadrant.

    Réponse
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 2, \space 0 \leq \theta \leq \frac{\pi}{2}\big\}\)

    4)\(R\) est la région du disque de rayon 3 centrée à l'origine.

    5)\(R\) est la région située entre les cercles de rayon 4 et de rayon 5 centrés à l'origine qui se trouve dans le second quadrant.

    Réponse
    \(R = \big\{(r, \theta)\,|\,4 \leq r \leq 5, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\)

    6)\(R\) est la région délimitée par l'\(y\)axe -et\(x = \sqrt{1 - y^2}\).

    7)\(R\) est la région délimitée par l'\(x\)axe -et\(y = \sqrt{2 - x^2}\).

    Réponse
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq \sqrt{2}, \space 0 \leq \theta \leq \pi\big\}\)

    8)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4x\big\}\)

    9)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4y\big\}\)

    Réponse
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 4 \space \sin \theta, \space 0 \leq \theta \leq \pi\big\}\)

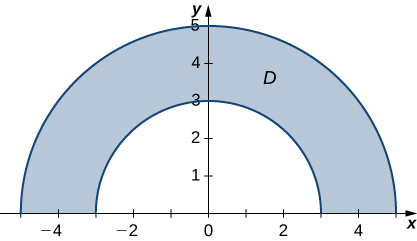
    Dans les exercices 10 à 15, le graphique de la région rectangulaire polaire\(D\) est donné. Exprimez\(D\) en coordonnées polaires.

    10)
    Un demi-anneau D est dessiné dans les premier et deuxième quadrants avec un rayon intérieur 3 et un rayon extérieur 5.
    11)
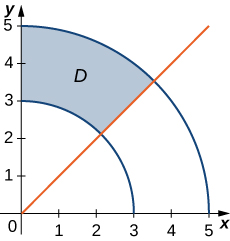
    Un secteur d'un anneau D est tracé entre thêta = pi/4 et thêta = pi/2 avec un rayon intérieur 3 et un rayon extérieur 5.
    Réponse
    \(D = \big\{(r, \theta)\,|\, 3 \leq r \leq 5, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}\big\}\)

    12)

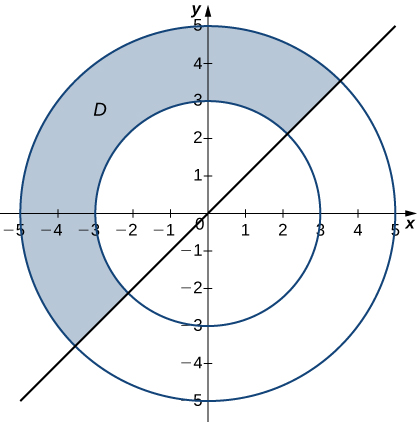
    Half of an annulus D is drawn between theta = pi/4 and theta = 5 pi/4 with inner radius 3 and outer radius 5.

    13)
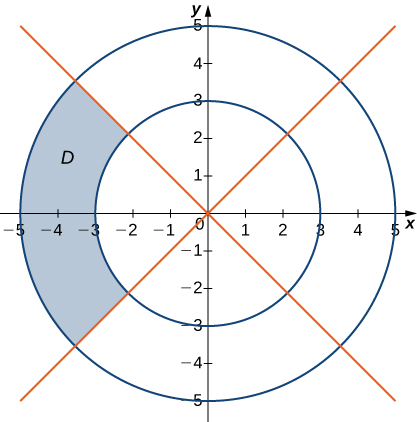
    Un secteur d'un anneau D est tracé entre thêta = 3 pi/4 et thêta = 5 pi/4 avec un rayon intérieur 3 et un rayon extérieur 5.

    Réponse
    \(D = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space \frac{3\pi}{4} \leq \theta \leq \frac{5\pi}{4}\big\}\)
    14) In the following graph, the region \(D\) is situated below \(y = x\) and is bounded by \(x = 1, \space x = 5\), and \(y = 0\).

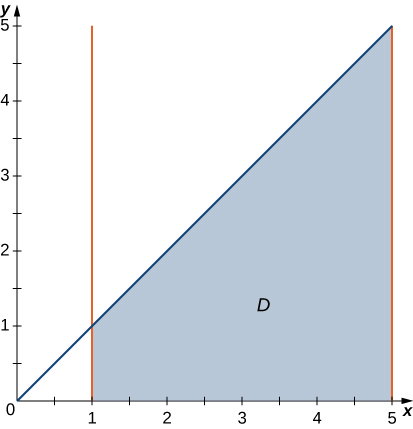
    A region D is given that is bounded by y = 0, x = 1, x = 5, and y = x, that is, a right triangle with a corner cut off.

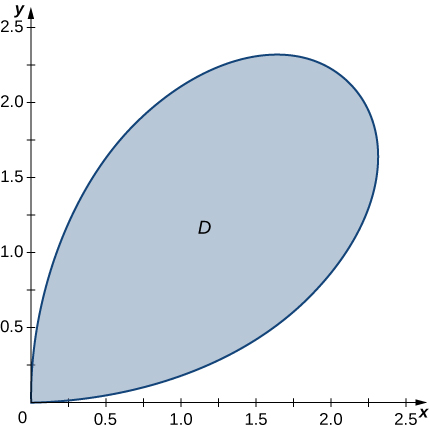
    15) Dans le graphique suivant, la région\(D\) est délimitée par\(y = x\) et\(y = x^2\).

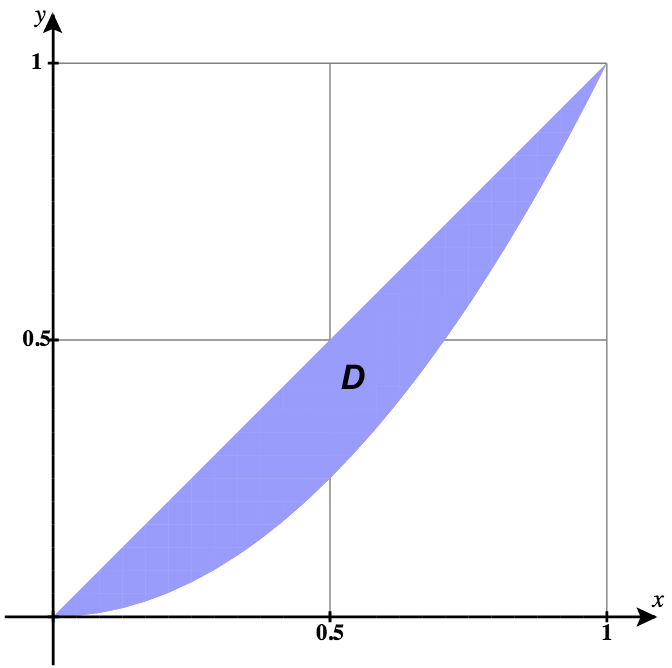
    Une région D est dessinée entre y = x et y = x au carré, ce qui ressemble à une lentille déformée, avec la partie bulbeuse en dessous de la partie droite.

    Réponse
    \(D = \big\{(r, \theta)\,|\,0 \leq r \leq \tan \theta \space \sec \theta, \space 0 \leq \theta \leq \frac{\pi}{4}\big\}\)

    Evaluating Polar Double Integrals

    In exercises 16 - 25, evaluate the double integral \(\displaystyle \iint_R f(x,y) \,dA\) over the polar rectangular region \(R\).

    16) \(f(x,y) = x^2 + y^2\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

    17) \(f(x,y) = x + y\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

    Answer
    \(0\)

    18) \(f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}\)

    19) \(f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}\)

    Answer
    \(\frac{63\pi}{16}\)

    20) \(f(x,y) = \sqrt[3]{x^2 + y^2}\), where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\).

    21) \(f(x,y) = x^4 + 2x^2y^2 + y^4\), where \(R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}\).

    Answer
    \(\frac{3367\pi}{18}\)

    22) \(f(x,y) = \sin (\arctan \frac{y}{x})\), where \(R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}\)

    23) \(f(x,y) = \arctan \left(\frac{y}{x}\right)\), where \(R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

    Answer
    \(\frac{35\pi^2}{576}\)

    24) \(\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}\)

    25) \(\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

    Answer
    \(\frac{7}{576}\pi^2 (21 - e + e^4)\)

    Converting Double Integrals to Polar Form

    In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.

    26) \(\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta\)

    27) \(\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta\)

    Answer
    \(\frac{5}{2} \ln (1 + \sqrt{2})\)

    28) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta\)

    29) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta\)

    Answer
    \(\frac{1}{6}(2 - \sqrt{2})\)

    In exercises 30 - 37, draw the region of integration, \(R\), labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.

    30) \(\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy\)

    31) \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy\)

    Answer
    \(\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}\)

    32) \(\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx\)

    33) \(\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx\)

    Answer
    \(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8\)

    34) \(\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx\)

    35) \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy\)

    Answer
    \(\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}\)

    36) \(\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy\)

    37) \(\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx\)

    Answer
    \(\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}\)

    38) Evaluate the integral \(\displaystyle \iint_D r \,dA\) where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

    39) Find the area of the region \(D\) bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

    Answer
    \(\frac{3\pi}{4}\)

    40) Evaluate the integral \(\displaystyle \iint_D r \,dA,\) where \(D\) is the region bounded by the part of the four-leaved rose \(r = \sin 2\theta\) situated in the first quadrant (see the following figure).

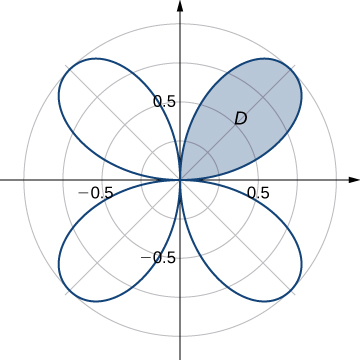
    A region D is drawn in the first quadrant petal of the four petal rose given by r = sin (2 theta).

    41) Déterminez la superficie totale de la région délimitée par la rose à quatre feuilles\(r = \sin 2\theta\) (voir la figure de l'exercice précédent).

    Réponse
    \(\frac{\pi}{2}\)

    42) Trouvez la zone de la région\(D\) qui est la région délimitée par\(y = \sqrt{4 - x^2}\)\(x = \sqrt{3}\),\(x = 2\), et\(y = 0\).

    43) Trouvez la zone de la région\(D\), qui est la région située à l'intérieur du disque\(x^2 + y^2 \leq 4\) et à droite de la ligne\(x = 1\).

    Réponse
    \(\frac{1}{3}(4\pi - 3\sqrt{3})\)

    44) Déterminez la valeur moyenne de la fonction\(f(x,y) = x^2 + y^2\) sur la région\(D\) délimitée par la courbe polaire\(r = \cos 2\theta\), où\(-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\) (voir le graphique suivant).

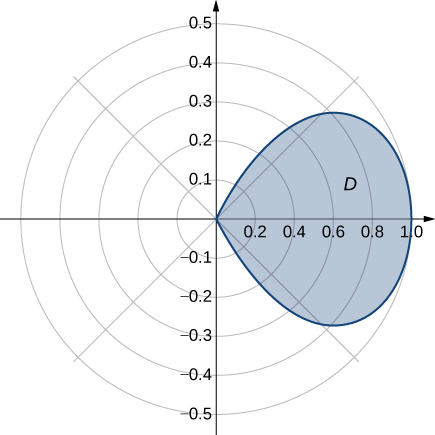
    Le pétale du premier/quatrième quadrant de la rose à quatre pétales donné par r = cos (2 thêta) est représenté.

    45) Déterminer la valeur moyenne de la fonction\(f(x,y) = \sqrt{x^2 + y^2}\) over the region \(D\) bounded by the polar curve \(r = 3\sin 2\theta\), where \(0 \leq \theta \leq \frac{\pi}{2}\) (see the following graph).

    The first-quadrant petal of the four-petal rose given by r = 3sin (2 theta) is shown.

    Réponse
    \(\frac{16}{3\pi}\)

    46) Trouvez le volume du solide situé dans le premier octant et délimité par le paraboloïde\(z = 1 - 4x^2 - 4y^2\) et les plans\(x = 0, \space y = 0\), et\(z = 0\).

    47) Détermine le volume du solide délimité par le paraboloïde\(z = 2 - 9x^2 - 9y^2\) et le plan\(z = 1\).

    Réponse
    \(\frac{\pi}{18}\)

    48)

    1. Trouvez le volume du solide\(S_1\) délimité par le cylindre\(x^2 + y^2 = 1\) et les plans\(z = 0\) et\(z = 1\).
    2. Déterminez le volume du solide\(S_2\) à l'extérieur du double cône\(x^2 + y^2 = 1\),\(z^2 = x^2 + y^2\) à l'intérieur du cylindre et au-dessus du plan\(z = 0\).
    3. Déterminez le volume du solide à l'intérieur du cône\(z^2 = x^2 + y^2\) et sous le plan\(z = 1\) en soustrayant les volumes des solides\(S_1\) et\(S_2\).

    49)

    1. Déterminez le volume du solide\(S_1\) à l'intérieur de la sphère unitaire\(x^2 + y^2 + z^2 = 1\) et au-dessus du plan\(z = 0\).
    2. Déterminez le volume du solide\(S_2\) à l'intérieur du double cône\((z - 1)^2 = x^2 + y^2\) et au-dessus du plan\(z = 0\).
    3. Déterminez le volume du solide à l'extérieur du double cône\((z - 1)^2 = x^2 + y^2\) et à l'intérieur de la sphère\(x^2 + y^2 + z^2 = 1\).
    Réponse
    a.\(\frac{2\pi}{3}\) ; b.\(\frac{\pi}{2}\) ; c.\(\frac{\pi}{6}\)

    Dans les exercices 50 à 51, des intégrales doubles spéciales sont présentées, particulièrement bien adaptées à l'évaluation en coordonnées polaires.

    50) La surface d'un cône circulaire droit avec hauteur\(h\) et rayon de base\(a\) peut être décrite par l'équation\(f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}\), où la pointe du cône se trouve\((0,0,h)\) et la base circulaire se trouve dans le\(xy\) plan -, centré à l'origine.
    Vérifiez que le volume d'un cône circulaire droit avec sa hauteur\(h\) et son rayon de base\(a\) est calculé\(V=\frac{1}{3}\pi a^2h\)\(\displaystyle \int\int_R f(x,y)\,dA\) en coordonnées polaires.

    51) Considérez\(\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.\)
    (a) Pourquoi cette intégrale est-elle difficile à évaluer en coordonnées rectangulaires, quelle que soit la région\(R\) ?
    (b)\(R\) Soit la région délimitée par le cercle de rayon\(a\) centré à l'origine. Evaluez l'intégrale double à l'aide des coordonnées polaires.
    (c) Prenez la limite de votre réponse à (b), comme\(a\to \infty\). Qu'est-ce que cela implique à propos du volume sous la surface de\(e^{-(x^2+y^2)}\) l'ensemble du\(xy\) plan ?

    Pour les deux exercices suivants, considérez un anneau sphérique, c'est-à-dire une sphère avec un trou cylindrique découpé de telle sorte que l'axe du cylindre passe par le centre de la sphère (voir la figure suivante).

    Un anneau sphérique est représenté, c'est-à-dire une sphère traversée par un trou cylindrique.

    52) Si la sphère a un rayon 4 et que le cylindre a un rayon 2, trouvez le volume de l'anneau sphérique.

    53) Un trou cylindrique de 6 cm de diamètre est percé à travers une sphère de 5 cm de rayon de telle sorte que l'axe du cylindre passe par le centre de la sphère. Trouvez le volume de l'anneau sphérique obtenu.

    Réponse
    \(\frac{256\pi}{3} \space \text{cm}^3\)

    54) Find the volume of the solid that lies under the double cone \(z^2 = 4x^2 + 4y^2\), inside the cylinder \(x^2 + y^2 = x\), and above the plane \(z = 0\).

    55) Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), inside the cylinder \(x^2 + y^2 = 1\) and above the plane \(z = 0\).

    Answer
    \(\frac{3\pi}{32}\)

    56) Find the volume of the solid that lies under the plane \(x + y + z = 10\) and above the disk \(x^2 + y^2 = 4x\).

    57) Find the volume of the solid that lies under the plane \(2x + y + 2z = 8\) and above the unit disk \(x^2 + y^2 = 1\).

    Answer
    \(4\pi\)

    58) A radial function \(f\) is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, \(f (x,y) = g(r)\), where \(r = \sqrt{x^2 + y^2}\). Show that if \(f\) is a continuous radial function, then

    \[\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r) \nonumber \] and \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

    59) Use the information from the preceding exercise to calculate the integral \(\displaystyle \iint_D (x^2 + y^2)^3 dA,\) where \(D\) is the unit disk.

    Answer
    \(\frac{\pi}{4}\)

    60) Let \(f(x,y) = \dfrac{F'(r)}{r}\) be a continuous radial function defined on the annular region \(D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), where \(r = \sqrt{x^2 + y^2}\), \(0 < R_1 < R_2\), and \(F\) is a differentiable function.

    Show that \(\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].\)

    61) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy\) where \(D\) is the annular region between the circles of radii 1 and 2 situated in the third quadrant.

    Answer
    \(\frac{1}{2} \pi e(e - 1)\)

    62) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is, \(f(x,y) = h(\theta)\), where \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

    Show that \(\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]\), where \(H\) is an antiderivative of \(h\).

    63) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{y^2}{x^2}\,dA,\) where \(D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.\)

    Answer
    \(\sqrt{3} - \frac{\pi}{4}\)

    64) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is \(f(x,y) = g(r)h(\theta)\), where \((x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\) with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\). Show that \[\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)], \nonumber \] where \(G\) and \(H\) are antiderivatives of \(g\) and \(h\), respectively.

    65) Evaluate \(\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,\) where \(D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\).

    Answer
    \(\frac{133}{864}\pi^2\)

    66) A spherical cap is the region of a sphere that lies above or below a given plane.

    a. Show that the volume of the spherical cap in the figure below is \(\frac{1}{6} \pi h (3a^2 + h^2)\).

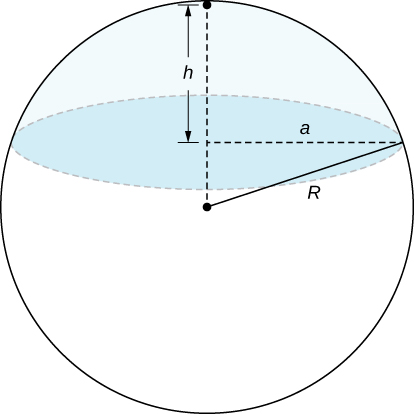
    A sphere of radius R has a circle inside of it h units from the top of the sphere. This circle has radius a, which is less than R.

    b. Un segment sphérique est le solide défini par l'intersection d'une sphère avec deux plans parallèles. Si la distance entre les plans est\(h\) indiquée, le volume du segment sphérique dans la figure ci-dessous est\(\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)\).

    b." data-type="media" id="fs-id1167793495515">Une sphère possède deux cercles parallèles à l'intérieur de celle-ci, distants de h unités. Le cercle supérieur a un rayon b et le cercle inférieur un rayon a. Notez que a b." src="https://math.libretexts.org/@api/dek...15_03_212.jpeg">

    67) En statistiques, la densité conjointe de deux événements indépendants et normalement distribués avec une moyenne

    • Template:ContribOpenStaxCalc
    • Problems 1, 2, 34 - 37 and 50 - 51 are from Apex Calculus, Chapter 13.3
    • Edited by Paul Seeburger (Monroe Community College)