15.3 : Intégrales doubles en coordonnées polaires
- Page ID
- 197492
- Reconnaissez le format d'une intégrale double sur une région rectangulaire polaire.
- Evaluez une intégrale double en coordonnées polaires à l'aide d'une intégrale itérée.
- Reconnaître le format d'une intégrale double sur une région polaire générale.
- Utilisez des intégrales doubles dans les coordonnées polaires pour calculer les surfaces et les volumes.
Les intégrales doubles sont parfois beaucoup plus faciles à évaluer si nous changeons les coordonnées rectangulaires en coordonnées polaires. Cependant, avant de décrire comment effectuer ce changement, nous devons établir le concept d'une double intégrale dans une région rectangulaire polaire.
Régions d'intégration rectangulaires polaires
Lorsque nous avons défini la double intégrale d'une fonction continue en coordonnées rectangulaires (par exemple,\(g\) sur une région\(R\) du\(xy\) plan -), nous l'avons\(R\) divisée en sous-rectangles dont les côtés sont parallèles aux axes des coordonnées. Ces côtés ont des\(x\) valeurs constantes et/ou des\(y\) valeurs constantes. En coordonnées polaires, la forme que nous utilisons est un rectangle polaire dont les côtés ont des\(r\) valeurs constantes et/ou des\(\theta\) valeurs constantes. Cela signifie que nous pouvons décrire un rectangle polaire comme sur la figure\(\PageIndex{1a}\), avec\(R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\).
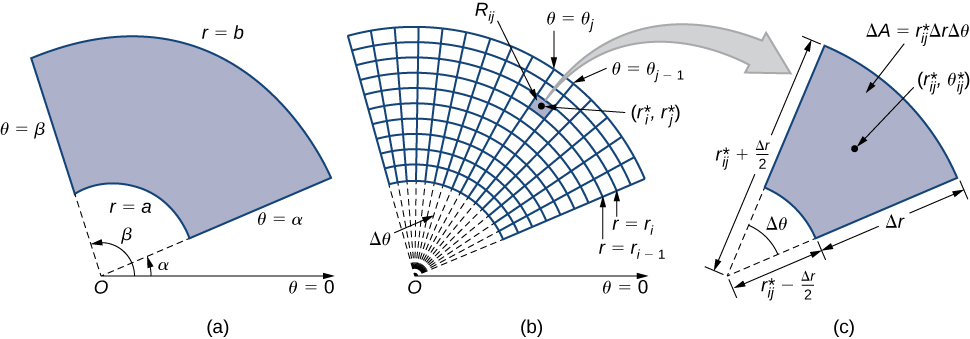
Dans cette section, nous cherchons à intégrer des rectangles polaires. Prenons l'exemple d'une fonction\(f(r,\theta)\) au-dessus d'un rectangle polaire\(R\). Nous divisons l'intervalle\([a,b]\) en\(m\) sous-intervalles\([r_{i-1}, r_i]\) de longueur\(\Delta r = (b - a)/m\) et divisons l'intervalle\([\alpha, \beta]\) en\(n\) sous-intervalles\([\theta_{i-1}, \theta_i]\) de largeur\(\Delta \theta = (\beta - \alpha)/n\). Cela signifie que les cercles\(r = r_i\) et\(\theta = \theta_i\) les rayons du rectangle polaire\(1 \leq i \leq m\) et le\(1 \leq j \leq n\) divisent\(R\) en sous-rectangles polaires plus petits\(R_{ij}\) (Figure\(\PageIndex{1b}\)).
Comme précédemment, nous devons trouver l'aire\(\Delta A\) du sous-rectangle polaire\(R_{ij}\) et le volume « polaire » de la fine boîte ci-dessus\(R_{ij}\). Rappelez-vous que, dans un cercle de rayon,\(r\) la longueur\(s\) d'un arc sous-tendu par un angle central de\(\theta\) radians est\(s = r\theta\). Remarquez que le rectangle polaire\(R_{ij}\) ressemble beaucoup à un trapèze avec des côtés parallèles\(r_{i-1}\Delta \theta\)\(r_i\Delta \theta\) et une largeur\(\Delta r\). Par conséquent, l'aire du sous-rectangle polaire\(R_{ij}\) est
\[\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_i \Delta \theta ). \nonumber \]
Simplifier et laisser
\[r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i) \nonumber \]
nous l'avons fait\(\Delta A = r_{ij}^* \Delta r \Delta \theta\).
Par conséquent, le volume polaire de la boîte mince ci-dessus\(R_{ij}\) (Figure\(\PageIndex{2}\)) est
\[f(r_{ij}^*, \theta_{ij}^*) \Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \nonumber \]
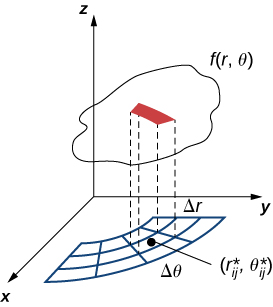
En utilisant la même idée pour tous les sous-rectangles et en additionnant les volumes des boîtes rectangulaires, nous obtenons une double somme de Riemann comme
\[\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]
Comme nous l'avons vu précédemment, nous obtenons une meilleure approximation du volume polaire du solide au-dessus de la région\(R\) lorsque nous le laissons\(m\)\(n\) grossir. Par conséquent, nous définissons le volume polaire comme la limite de la double somme de Riemann,
\[V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]
Cela devient l'expression de la double intégrale.
La double intégrale de la fonction\(f(r, \theta)\) sur la région rectangulaire polaire\(R\) dans le\(r\theta\) plan -est définie comme
\[\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[4pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align} \nonumber \]
Encore une fois, tout comme dans la section sur les intégrales doubles sur des régions rectangulaires, l'intégrale double sur une région rectangulaire polaire peut être exprimée sous la forme d'une intégrale itérée en coordonnées polaires. Par conséquent,
\[\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]
Notez que l'expression pour\(dA\) est remplacée par\(r \, dr \, d\theta\) lorsque vous travaillez en coordonnées polaires. Une autre façon d'examiner la double intégrale polaire consiste à modifier la double intégrale en coordonnées rectangulaires par substitution. Lorsque la fonction\(f\) est donnée en termes d'\(y\)utilisation\(x\)\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\) et qu'elle la\(dA = r \, dr \, d\theta\) modifie en
\[\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta. \nonumber \]
Notez que toutes les propriétés répertoriées dans la section sur les intégrales doubles sur les régions rectangulaires pour l'intégrale double en coordonnées rectangulaires s'appliquent également à la double intégrale en coordonnées polaires, nous pouvons donc les utiliser sans hésitation.
Esquissez la région rectangulaire polaire
\[R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber \]
Solution
Comme nous pouvons le voir sur la figure\(\PageIndex{3}\),\(r = 1\) ce\(r = 3\) sont des cercles de rayon 1 et 3\(0 \leq \theta \leq \pi\) qui couvrent toute la moitié supérieure du plan. La région\(R\) ressemble donc à une bande semi-circulaire.
Maintenant que nous avons esquissé une région rectangulaire polaire, montrons comment évaluer une double intégrale sur cette région en utilisant des coordonnées polaires.
Évaluer l'intégrale\(\displaystyle \iint_R 3x \, dA\) sur la région\(R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.\)
Solution
Nous esquissons d'abord une figure similaire à la figure\(\PageIndex{3}\), mais avec un rayon extérieur\(r=2\). Sur la figure, nous pouvons voir que nous avons
\[\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta \quad\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta=0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta \quad\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta \\ &= 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}\]
Esquissez la région\(D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}\) et évaluez\(\displaystyle \iint_R x \, dA\).
- Allusion
-
Suivez les étapes de l'exemple\(\PageIndex{1A}\).
- Réponse
-
\(\frac{14}{3}\)
Evaluer l'intégrale
\[\iint_R (1 - x^2 - y^2) \,dA \nonumber \]
où\(R\) est le cercle unitaire sur le\(xy\) plan.
Solution
La région\(R\) est un cercle unitaire, nous pouvons donc la décrire ainsi\(R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}\).
En utilisant la conversion\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\)\(dA = r \, dr \, d\theta\), et nous avons
\[\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta \\[4pt] &= \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta \\&= \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}\]
Évaluez l'intégrale\[\displaystyle \iint_R (x + y) \,dA \nonumber \] où\(R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.\)
Solution
Nous pouvons voir qu'il\(R\) s'agit d'une région annulaire qui peut être convertie en coordonnées polaires et décrite comme\(R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}\) (voir le graphique suivant).

Par conséquent, en utilisant la conversion\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), et\(dA = r \, dr \, d\theta\), nous avons
\[\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\ &= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}\]
Evaluez l'intégrale\[ \displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber \] où\(R\) se trouve le cercle de rayon 2 sur le\(xy\) plan.
- Allusion
-
Suivez les étapes de l'exemple précédent.
- Réponse
-
\(8\pi\)
Régions polaires générales d'intégration
Pour évaluer la double intégrale d'une fonction continue par des intégrales itérées sur des régions polaires générales, nous considérons deux types de régions, analogues aux régions de type I et de type II, comme indiqué pour les coordonnées rectangulaires dans la section sur les intégrales doubles sur les régions générales. Il est plus courant d'écrire des équations polaires sous\(r = f(\theta)\) la forme de. Nous décrivons donc une région polaire générale comme\(R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\) (Figure\(\PageIndex{5}\)).\(\theta = f(r)\)
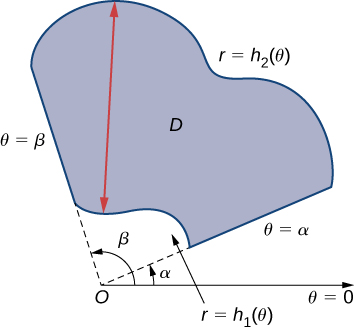
S'il\(f(r, \theta)\) est continu sur une région polaire générale\(D\) comme décrit ci-dessus, alors
\[\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta. \nonumber \]
Evaluer l'intégrale
\[\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber \]
où\(D\) est la région délimitée par l'axe polaire et la moitié supérieure de la cardioïde\(r = 1 + \cos \, \theta\).
Solution
Nous pouvons décrire la région\(D\)\(\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\} \) comme indiqué sur la figure\(\PageIndex{6}\).
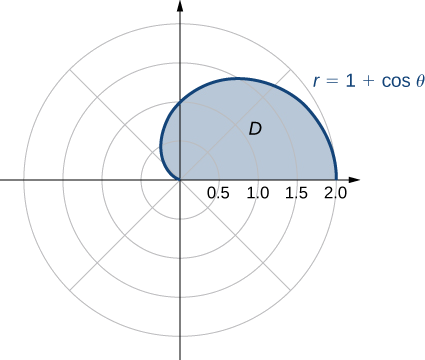
Par conséquent, nous avons
\[\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\ &= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ &= \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ &= - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}\]
Evaluer l'intégrale
\[\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber \]
où\(D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}\).
- Allusion
-
Représentez la région sous forme graphique et suivez les étapes de l'exemple précédent.
- Réponse
-
\(\frac{\pi}{8}\)
Zones et volumes polaires
Comme pour les coordonnées rectangulaires, si un solide\(S\) est délimité par la surface\(z = f(r, \theta)\), ainsi que par les surfaces\(r = a, \, r = b, \, \theta = \alpha\)\(\theta = \beta\), et que nous pouvons trouver le volume\(V\) de\(S\) par double intégration, comme
\[V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta. \nonumber \]
Si la base du solide peut être décrite comme\(D = \{(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\) suit, alors la double intégrale du volume devient
\[V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]
Nous illustrons cette idée à l'aide de quelques exemples.
Déterminez le volume du solide situé sous le paraboloïde\(z = 1 - x^2 - y^2\) et au-dessus du cercle unitaire sur le\(xy\) plan (Figure\(\PageIndex{7}\)).
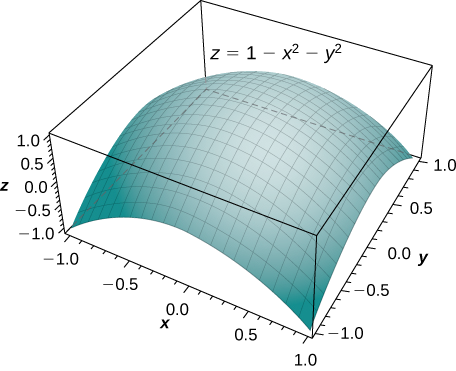
Solution
Par la méthode de double intégration, nous pouvons voir que le volume est l'intégrale itérée du formulaire
\[\displaystyle \iint_R (1 - x^2 - y^2)\,dA \nonumber \]
où\(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}\).
Cette intégration a déjà été montrée dans l'exemple\(\PageIndex{2A}\), de sorte que le volume est en unités\(\frac{\pi}{2}\) cubiques.
Déterminez le volume du solide situé sous le paraboloïde\(z = 4 - x^2 - y^2\) et au-dessus du disque\((x - 1)^2 + y^2 = 1\) sur le\(xy\) plan. Voir le paraboloïde sur la figure\(\PageIndex{8}\) croisant le cylindre\((x - 1)^2 + y^2 = 1\) au-dessus du\(xy\) plan.
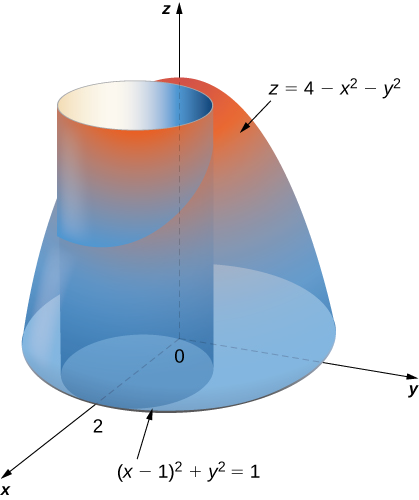
Solution
Changez d'abord le disque\((x - 1)^2 + y^2 = 1\) en coordonnées polaires. Nous avons élargi le terme carré\(x^2 - 2x + 1 + y^2 = 1\). Simplifiez ensuite pour obtenir ce qui\(x^2 + y^2 = 2x\), en coordonnées polaires, devient,\(r^2 = 2r \, \cos \, \theta\) puis\(r = 0\) soit\(r = 2 \, \cos \, \theta\). De même, l'équation du paraboloïde devient\(z = 4 - r^2\). Par conséquent, nous pouvons décrire le disque\((x - 1)^2 + y^2 = 1\) sur le\(xy\) plan -comme étant la région
\[D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber \]
Ainsi, le volume du solide limité en haut par le paraboloïde\(z = 4 - x^2 - y^2\) et en dessous par\(r = 2 \, \cos \theta\) est
\[\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta \\&= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\ &= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\ &= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^4\theta]\,d\theta \\&= \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}\]
Remarquez dans l'exemple suivant que l'intégration n'est pas toujours facile avec les coordonnées polaires. La complexité de l'intégration dépend de la fonction et également de la région dans laquelle nous devons réaliser l'intégration. Si la région a une expression plus naturelle en coordonnées polaires ou si\(f\) elle possède une antidérivée plus simple en coordonnées polaires, le changement des coordonnées polaires est approprié ; sinon, utilisez des coordonnées rectangulaires.
Déterminez le volume de la région située sous le paraboloïde\(z = x^2 + y^2\) et au-dessus du triangle délimité par les lignes\(y = x, \, x = 0\), et\(x + y = 2\) dans le\(xy\) plan.
Solution
Examinez d'abord la région sur laquelle nous devons placer la double intégrale et le paraboloïde qui l'accompagne.
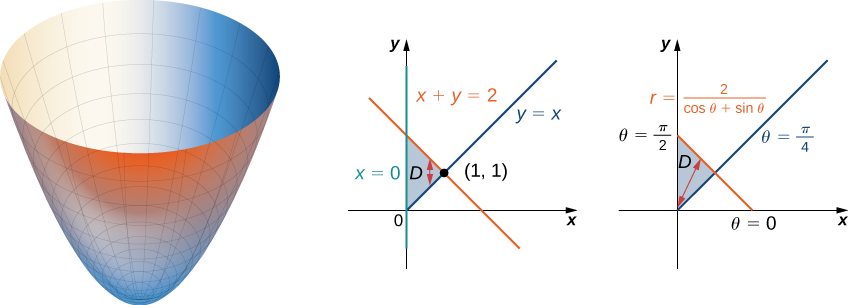
La région\(D\) est\(\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}\). Conversion des lignes\(y = x, \, x = 0\) et du\(xy\) plan\(x + y = 2\) en fonctions de\(r\) et\(\theta\) que nous avons\(\theta = \pi/4, \, \theta = \pi/2\)\(r = 2 / (\cos \, \theta + \sin \, \theta)\), respectivement. En traçant la région sur le plan\(xy\) -, nous voyons à quoi elle ressemble\(D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}\).
Maintenant, la conversion de l'équation de la surface donne\(z = x^2 + y^2 = r^2\). Par conséquent, le volume du solide est donné par la double intégrale
\[\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta \\&= \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ (\cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta \\ &= \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta \\ &= \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right)^4 d\theta \\&= 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}\]
Comme vous pouvez le constater, cette intégrale est très compliquée. Nous pouvons donc plutôt évaluer cette double intégrale en coordonnées rectangulaires comme
\[V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx. \nonumber \]
Évaluer les dons
\[\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx \\&= \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 \\&= \frac{4}{3} \; \text{units}^3. \end{align*}\]
Pour répondre à la question de savoir comment sont trouvées les formules pour les volumes de différents solides standard tels qu'une sphère, un cône ou un cylindre, nous voulons montrer un exemple et déterminer le volume d'un cône arbitraire.
Utilisez les coordonnées polaires pour trouver le volume à l'intérieur du cône\(z = 2 - \sqrt{x^2 + y^2}\) et au-dessus du\(xy\) plan.
Solution
La région\(D\) d'intégration est la base du cône, qui semble être un cercle sur le\(xy\) plan (Figure\(\PageIndex{10}\)).
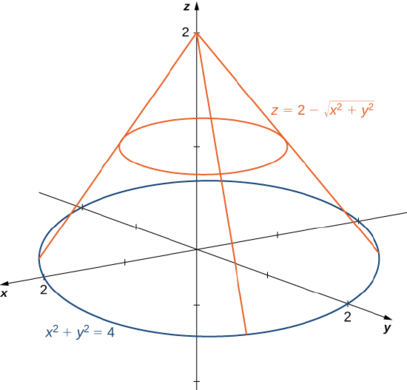
On trouve l'équation du cercle en définissant\(z = 0\) :
\[\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}\]
Cela signifie que le rayon du cercle est\(2\) tel pour l'intégration que nous avons\(0 \leq \theta \leq 2\pi\) et\(0 \leq r \leq 2\). En substituant\(x = r \, \cos \theta\) et\(y = r \, \sin \, \theta\) dans l'équation\(z = 2 - \sqrt{x^2 + y^2}\) que nous avons\(z = 2 - r\). Par conséquent, le volume du cône est
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber \]
AnalyseNotez que si nous devions trouver le volume d'un cône arbitraire avec des\(\alpha\) unités de rayon et des\(h\) unités de hauteur, alors l'équation du cône serait\(z = h - \frac{h}{a}\sqrt{x^2 + y^2}\).
Nous pouvons toujours utiliser Figure\(\PageIndex{10}\) et configurer l'intégrale comme
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber \]
En évaluant l'intégrale, nous obtenons\(\frac{1}{3} \pi a^2 h\).
Utilisez les coordonnées polaires pour trouver une intégrale itérée permettant de déterminer le volume du solide entouré par les paraboloïdes\(z = x^2 + y^2\) et\(z = 16 - x^2 - y^2\).
- Allusion
-
L'esquisse des graphiques peut vous aider.
- Réponse
-
\[V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber \]
Trouvez la zone délimitée par le cercle\(r = 3 \, \cos \, \theta\) et le cardioïde\(r = 1 + \cos \, \theta\).
Solution
Tout d'abord, tracez les graphes de la région (Figure\(\PageIndex{12}\)).
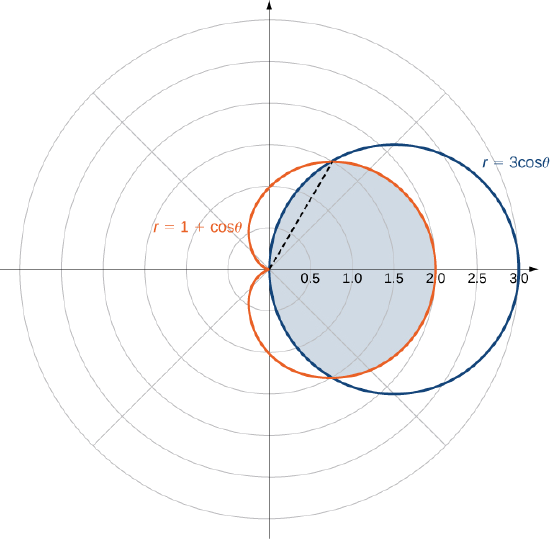
Nous pouvons à partir de la symétrie du graphe dont nous avons besoin pour trouver les points d'intersection. Mettre les deux équations égales l'une à l'autre donne
\[3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber \]
L'un des points d'intersection est\(\theta = \pi/3\). La zone au-dessus de l'axe polaire se compose de deux parties, l'une étant définie par le cardioïde de\(\theta = 0\) à\(\theta = \pi/3\) et l'autre par le cercle de\(\theta = \pi/3\) à\(\theta = \pi/2\). Par symétrie, l'aire totale est le double de la surface au-dessus de l'axe polaire. Ainsi, nous avons
\[A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber \]
En évaluant chaque pièce séparément, nous constatons que la zone est
\[A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber \]
Trouvez la zone située à l'intérieur du cardioïde\(r = 3 - 3 \, \sin \theta\) et à l'extérieur du cardioïde\(r = 1 + \sin \theta\).
- Allusion
-
Esquissez le graphique et résolvez les points d'intersection.
- Réponse
-
\[A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber \]
Evaluer l'intégrale
\[\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber \]
Solution
Il s'agit d'une intégrale inappropriée parce que nous nous intégrons dans une région sans limites\(R^2\). En coordonnées polaires, l'ensemble du plan\(R^2\) peut être vu comme\(0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty\).
En utilisant les changements de variables des coordonnées rectangulaires aux coordonnées polaires, nous avons
\[\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\ &=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\ &= \frac{\pi}{10}. \end{align*}\]
Evaluer l'intégrale
\[\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber \]
- Allusion
-
Effectuez la conversion vers le système de coordonnées polaires.
- Réponse
-
\(\frac{\pi}{4}\)
Concepts clés
- Pour appliquer une double intégrale à une situation à symétrie circulaire, il est souvent pratique d'utiliser une intégrale double en coordonnées polaires. Nous pouvons appliquer ces intégrales doubles sur une région polaire rectangulaire ou une région polaire générale, en utilisant une intégrale itérée similaire à celles utilisées pour les intégrales doubles rectangulaires.
- La zone\(dA\) en coordonnées polaires devient\(r \, dr \, d\theta\).
- Utilisez\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\) et\(dA = r \, dr \, d\theta\) pour convertir une intégrale en coordonnées rectangulaires en une intégrale en coordonnées polaires.
- Utilisez\(r^2 = x^2 + y^2\) et\(\theta = tan^{-1} \left(\frac{y}{x}\right)\) pour convertir une intégrale en coordonnées polaires en une intégrale en coordonnées rectangulaires, si nécessaire.
- Pour trouver le volume en coordonnées polaires délimitées au-dessus par une surface\(z = f(r, \theta)\) au-dessus d'une région du\(xy\) plan, utilisez une double intégrale en coordonnées polaires.
Équations clés
- Intégrale double sur une région rectangulaire polaire\(R\)
\[\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber \]
- Intégrale double sur une région polaire générale
\[\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber \]
Lexique
- rectangle polaire
- la région comprise entre les cercles\(r = a\)\(r = b\) et les angles\(\theta = \alpha\) et\(\theta = \beta\) ; elle est décrite comme\(R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\)



Comme pour les coordonnées rectangulaires, nous pouvons également utiliser les coordonnées polaires pour trouver les zones de certaines régions à l'aide d'une double intégrale. Comme auparavant, nous devons comprendre la région dont nous voulons calculer la superficie. L'esquisse d'un graphique et l'identification de la région peuvent être utiles pour comprendre les limites de l'intégration. En général, la formule de superficie en cas de double intégration ressemblera à
\[\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta. \nonumber \]
Exemple\(\PageIndex{6A}\): Finding an Area Using a Double Integral in Polar Coordinates
Évaluez la zone délimitée par la courbe\(r = \cos \, 4\theta\).
Solution
L'esquisse du graphique de la fonction\(r = \cos \, 4\theta\) révèle qu'il s'agit d'une rose polaire à huit pétales (voir la figure suivante).
En utilisant la symétrie, nous pouvons voir que nous devons trouver l'aire d'un pétale, puis la multiplier par 8. Notez que les valeurs\(\theta\) pour lesquelles le graphe passe par l'origine sont les zéros de la fonction\(\cos \, 4\theta\), et ce sont des multiples impairs de\(\pi/8\). Ainsi, l'un des pétales correspond aux valeurs de\(\theta\) dans l'intervalle\([-\pi/8, \pi/8]\). Par conséquent, l'aire délimitée par la courbe\(r = \cos \, 4\theta\) est
\[\begin{align*} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\ &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \\ &= 8 \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta \\&= 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] \\&= 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align*}\]