15.2E : Exercices pour la section 15.2

Last updated
Save as PDF

Page ID: 197441

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) La région$D$ délimitée par$y = x^3, \space y = x^3 + 1, \space x = 0,$ et$x = 1$ comme indiqué dans la figure suivante.

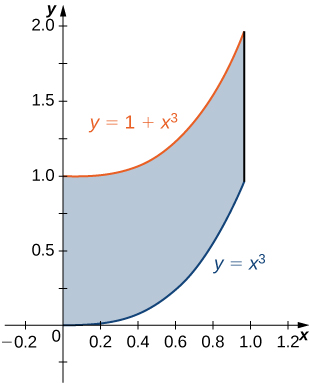
$Une région est délimitée par y = 1 + x en cubes, y = x en cubes, x = 0 et x = 1.$

a. Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type I mais pas Type II

b. Trouvez la superficie de la région$D$.

c. Find the average value of the function $f(x,y) = 3xy$ on the region graphed in the previous exercise.

Answer: $\frac{27}{20}$

2) The region $D$ bounded by $y = \sin x, \space y = 1 + \sin x, \space x = 0$, and $x = \frac{\pi}{2}$ as given in the following figure.

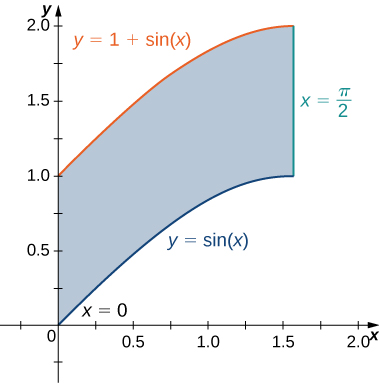
$A region is bounded by y = 1 + sin x, y = sin x, x = 0, and x = pi/2.$

a. Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type I mais pas Type II

b. Déterminez la zone de la région$D$.

Réponse: $\frac{\pi}{2}\, \text{units}^2$

c. Déterminez la valeur moyenne de la fonction$f(x,y) = \cos x$ sur la région$D$.

3) La région$D$ délimitée par$x = y^2 - 1$ et$x = \sqrt{1 - y^2}$ comme indiqué dans la figure suivante.

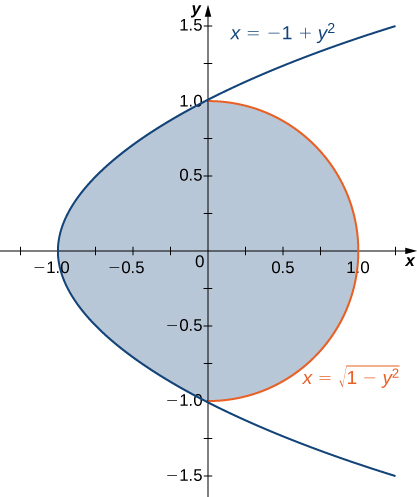
$Une région est délimitée par x = moins 1 + y au carré et x = la racine carrée de la quantité (1 moins y au carré).$

a. Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type II mais pas Type I

b. Trouvez le volume du solide sous le graphique de la fonction$f(x,y) = xy + 1$ and above the region $D$.

Answer: $\frac{1}{6}(8 + 3\pi)\, \text{units}^3$

4) The region $D$ bounded by $y = 0, \space x = -10 + y,$ and $x = 10 - y$ as given in the following figure.

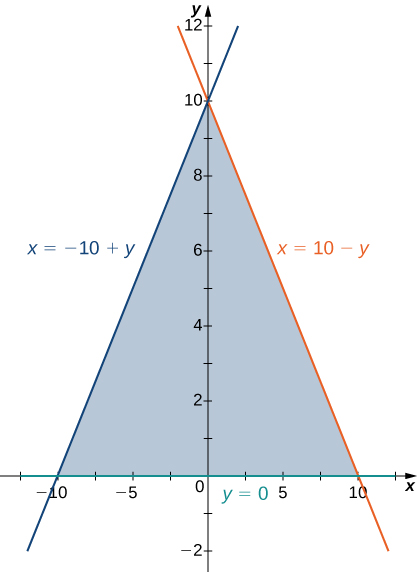
$A region is bounded by x = negative 10 + y, x = 10 minus y, and y = 0.$

a. Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type II mais pas Type I

b. Déterminez le volume du solide sous le graphique de la fonction$f(x,y) = x + y$ et au-dessus de la région dans la figure de l'exercice précédent.

Réponse: $\frac{1000}{3}\, \text{units}^3$

5) La région$D$ délimitée par$y = 0, \space x = y - 1, \space x = \frac{\pi}{2}$, comme indiqué dans la figure suivante.

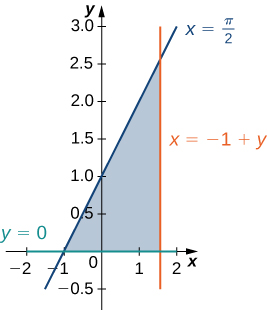
$Une région est délimitée par x = pi/2, y = 0 et x = négatif 1 + y.$

Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type I et Type II

6) La région$D$ bounded by $y = 0$ and $y = x^2 - 1$ as given in the following figure.

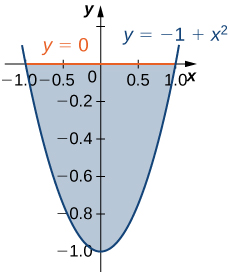
$A region is bounded by y = 0 and y = negative 1 + x squared.$

Classez cette région comme étant verticale simple (type I) ou simple horizontalement (type II).

Tipo :: Type I et Type II

7)$D$ Soit la région délimitée par les courbes des équations$y = \cos x$$y = 4 - x^2$ et par l'$x$axe. Expliquez pourquoi$D$ il n'est ni de type I ni de type II.

Réponse: La région n'$D$est pas de type I : elle ne se situe pas entre deux lignes verticales et les graphes de deux fonctions continues$g_1(x)$ et$g_2(x)$. La région n'est pas de type II : elle ne se situe pas entre deux lignes horizontales et les graphes de deux fonctions continues$h_1(y)$ et$h_2(y)$.

8)$D$ Soit la région délimitée par les courbes des équations$y = x, \space y = -x$ et$y = 2 - x^2$. Expliquez pourquoi$D$ il n'est ni de type I ni de type II.

Dans les exercices 9 à 14, évaluez la double intégrale$\displaystyle \iint_D f(x,y) \,dA$ sur la région$D$.

9)$f(x,y) = 1$ et

$D = \big\{(x,y)| \, 0 \leq x \leq \frac{\pi}{2}, \space \sin x \leq y \leq 1 + \sin x \big\}$

Réponse: $\frac{\pi}{2}$

10)$f(x,y) = 2$ et

$D = \big\{(x,y)| \, 0 \leq y \leq 1, \space y - 1 \leq x \leq \arccos y \big\}$

11)$f(x,y) = xy$ et

$D = \big\{(x,y)| \, -1 \leq y \leq 1, \space y^2 - 1 \leq x \leq \sqrt{1 - y^2} \big\}$

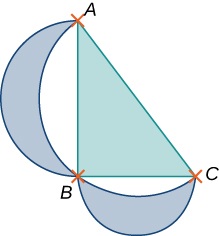
Réponse: $0$

12)$f(x,y) = \sin y$ et$D$ est la région triangulaire avec des sommets$(0,0), \space (0,3)$, et$(3,0)$

13)$f(x,y) = -x + 1$ et$D$ est la région triangulaire avec des sommets$(0,0), \space (0,2)$, et$(2,2)$

Réponse: $\frac{2}{3}$

14)$f(x,y) = 2x + 4y$ et

$D = \big\{(x,y)|\, 0 \leq x \leq 1, \space x^3 \leq y \leq x^3 + 1 \big\}$

Dans les exercices 15 à 20, évaluez les intégrales itérées.

15)$\displaystyle \int_0^1 \int_{2\sqrt{x}}^{2\sqrt{x}+1} (xy + 1) \,dy \space dx$

Réponse: $\frac{41}{20}$

16)$\displaystyle \int_0^3 \int_{2x}^{3x} (x + y^2) \,dy \space dx$

17)$\displaystyle \int_1^2 \int_{-u^2-1}^{-u} (8 uv) \,dv \space du$

Réponse: $-63$

18)$\displaystyle \int_e^{e^2} \int_{\ln u}^2 (v + \ln u) \,dv \space du$

19)$\displaystyle \int_0^{1/2} \int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}} 4 \,dx \space dy$

Réponse: $\pi$

(20)$\displaystyle \int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} (2x + 4y^3) \,dx \space dy$

21)$D$ Soit la région délimitée par$y = 1 - x^2, \space y = 4 - x^2$ les$y$ axes$x$ - et -.

a. Démontrez cela$\displaystyle \iint_D x\,dA = \int_0^1 \int_{1-x^2}^{4-x^2} x \space dy \space dx + \int_1^2 \int_0^{4-x^2} x \space dy \space dx$ en divisant la région$D$ en deux régions de type I.

b. Évaluer l'intégrale$\displaystyle \iint_D x \,dA.$

22)$D$ Soit la région délimitée par$y = 1, \space y = x, \space y = \ln x$ et l'$x$axe.

a. Démontrez cela$\displaystyle \iint_D y^2 \,dA = \int_{-1}^0 \int_{-x}^{2-x^2} y^2 dy \space dx + \int_0^1 \int_x^{2-x^2} y^2 dy \space dx$ en divisant la région$D$ en deux régions de type I, où$D = \big\{(x,y)\,|\,y \geq x, y \geq -x, \space y \leq 2-x^2\big\}$.

b. Évaluer l'intégrale$\displaystyle \iint_D y^2 \,dA.$

23)$D$ Soit la région délimitée par$y = x^2$$y = x + 2$, et$y = -x$.

a. Montrez cela$\displaystyle \iint_D x \, dA = \int_0^1 \int_{-y}^{\sqrt{y}} x \space dx \space dy + \int_1^4 \int_{y-2}^{\sqrt{y}} x \space dx \space dy$ en divisant la région$D$ en deux régions de type II, où$D = \big\{(x,y)\,|\,y \geq x^2, \space y \geq -x, \space y \leq x + 2\big\}$.

b. Évaluer l'intégrale$\displaystyle \iint_D x \,dA.$

Réponse: a. Les réponses peuvent varier ;
b.$\frac{8}{12}$

24) La région$D$ délimitée par$x = 0, y = x^5 + 1$ et$y = 3 - x^2$ est illustrée dans la figure suivante. Trouvez la zone$A(D)$ de la région$D$.

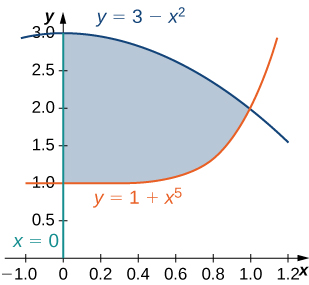
$Une région est délimitée par y = 1 + x à la cinquième puissance, y = 3 moins x au carré et x = 0.$

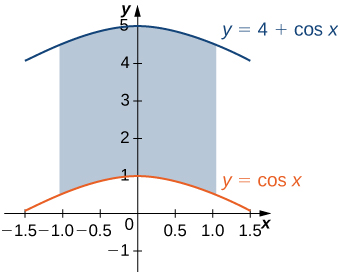
25) La région$D$ bounded by $y = \cos x, \space y = 4 + \cos x$, and $x = \pm \frac{\pi}{3}$ is shown in the following figure. Find the area $A(D)$ of the region $D$.

$A region is bounded by y = cos x, y = 4 + cos x, x = negative 1, and x = 1.$

Réponse: $\frac{8\pi}{3}$

26) Déterminez la superficie$A(D)$ de la région$D = \big\{(x,y)| \, y \geq 1 - x^2, y \leq 4 - x^2, \space y \geq 0, \space x \geq 0 \big\}$.

27)$D$ Soit la région délimitée par$ y = 1, \space y = x, \space y = \ln x$ et l'$x$axe. Trouvez la zone$A(D)$ de la région$D$.

Réponse: $\left(e - \frac{3}{2}\right)\, \text{units}^2$

28) Trouvez la valeur moyenne de la fonction$f(x,y) = \sin y$ sur la région triangulaire avec des sommets$(0,0), \space (0,3)$, et$(3,0)$.

29) Trouvez la valeur moyenne de la fonction$f(x,y) = -x + 1$ sur la région triangulaire avec des sommets$(0,0), \space (0,2)$, et$(2,2)$.

Réponse: La valeur moyenne de$f$ sur cette région triangulaire est$\frac{1}{3}.$

Dans les exercices 30 à 33, modifiez l'ordre d'intégration et évaluez l'intégrale.

(30)$\displaystyle \int_{-1}^{\pi/2} \int_0^{x+1} \sin x \, dy \, dx$

31)$\displaystyle \int_0^1 \int_{x-1}^{1-x} x \, dy \, dx$

Réponse: $\displaystyle \int_0^1 \int_{x-1}^{1-x} x \space dy \space dx = \int_{-1}^0 \int_0^{y+1} x \space dx \space dy + \int_0^1 \int_0^{1-y} x \space dx \space dy = \frac{1}{3}$

32)$\displaystyle \int_{-1}^0 \int_{-\sqrt{y+1}}^{\sqrt{y+1}} y^2 dx \space dy$

33)$\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy$

Réponse: $\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy = \int_1^2 \int_{-\sqrt{x^2-1}}^{\sqrt{x^2-1}} y \space dy \space dx = 0$

34) La région$D$ est illustrée dans la figure suivante. Évaluez la double intégrale$\displaystyle \iint_D (x^2 + y) \,dA$ en utilisant l'ordre d'intégration le plus simple.

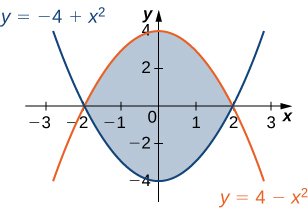
$Une région est délimitée par y = moins 4 + x au carré et y = 4 moins x au carré.$

35) La région$D$ is shown in the following figure. Evaluate the double integral $\displaystyle \iint_D (x^2 - y^2) \,dA$ by using the easier order of integration.

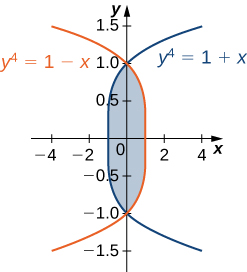
$A region is bounded by y to the fourth power = 1 minus x and y to the fourth power = 1 + x.$

Réponse: $\displaystyle \iint_D (x^2 - y^2) dA = \int_{-1}^1 \int_{y^4-1}^{1-y^4} (x^2 - y^2)dx \space dy = \frac{464}{4095}$

36) Déterminez le volume du solide sous la surface$z = 2x + y^2$ et au-dessus de la région délimitée par$y = x^5$ et$y = x$.

37) Déterminez le volume du solide sous le plan$z = 3x + y$ et au-dessus de la région déterminée par$y = x^7$ et$y = x$.

Réponse: $\frac{4}{5}\, \text{units}^3$

38) Trouvez le volume du solide sous le plan$z = 3x + y$ et au-dessus de la région délimitée par$x = \tan y, \space x = -\tan y$, et$x = 1$.

39) Déterminez le volume du solide sous la surface$z = x^3$ et au-dessus de la région plane délimitée par$x = \sin y, \space x = -\sin y$, et$x = 1$.

Réponse: $\frac{5\pi}{32}\, \text{units}^3$

40)$g$ Soit une fonction positive, croissante et dérivable sur l'intervalle$[a,b]$. Montrez que le volume du solide sous la surface$z = g'(x)$ et au-dessus de la région délimitée par$y = 0, \space y = g(x), \space x = a$ et$x = b$ est donné par$\frac{1}{2}(g^2 (b) - g^2 (a))$.

41)$g$ Soit une fonction positive, croissante et dérivable sur l'intervalle$[a,b]$ et$k$ soit un nombre réel positif. Montrez que le volume du solide sous la surface$z = g'(x)$ et au-dessus de la région délimitée par$y = g(x), \space y = g(x) + k, \space x = a$, et$x = b$ est donné par$k(g(b) - g(a)).$

42) Trouvez le volume du solide situé dans le premier octant et déterminé par les plans$z = 2$$z = 0, \space x + y = 1, \space x = 0$, et$y = 0$.

43) Trouvez le volume du solide situé dans le premier octant et délimité par les plans$x + 2y = 1$$x = 0, \space z = 4$, et$z = 0$.

Réponse: $1\, \text{units}^3$

44) Trouvez le volume du solide délimité par les plans$x + y = 1, \space x - y = 1, \space x = 0, \space z = 0$, et$z = 10$.

45) Trouvez le volume du solide délimité par les plans$x + y = 1, \space x - y = 1, \space x + y = -1\space x - y = -1, \space z = 1$, et$z = 0$

Réponse: $2\, \text{units}^3$

46)$S_2$ Soit$S_1$ les solides situés dans le premier octant sous les plans$x + y + z = 1$ et$x + y + 2z = 1$ respectivement, et$S$ soit le solide situé entre$S_1, \space S_2, \space x = 0$, et$y = 0$.

Détermine le volume du solide$S_1$.
Détermine le volume du solide$S_2$.
Déterminez le volume du solide$S$ en soustrayant les volumes des solides$S_1$ et$S_2$.

47)$S_2$ Soit$S_1$ les solides situés dans le premier octant sous les plans$2x + 2y + z = 2$ et$x + y + z = 1$ respectivement, et$S$ soit le solide situé entre$S_1, \space S_2, \space x = 0$, et$y = 0$.

Détermine le volume du solide$S_1$.
Détermine le volume du solide$S_2$.
Déterminez le volume du solide$S$ en soustrayant les volumes des solides$S_1$ et$S_2$.

Réponse: a.$\frac{1}{3}\, \text{units}^3$
b.$\frac{1}{6}\, \text{units}^3$
c.$\frac{1}{6}\, \text{units}^3$

48)$S_2$ Soit$S_1$ les solides situés dans le premier octant sous le plan$x + y + z = 2$ et sous la sphère$x^2 + y^2 + z^2 = 4$, respectivement. Si le volume du solide$S_2$ est,$\frac{4\pi}{3}$ déterminez le volume du solide$S$ situé entre$S_1$ et$S_2$ en soustrayant les volumes de ces solides.

49)$S_2$ Soit$S_1$ les solides situés dans le premier octant sous le plan$x + y + z = 2$ et délimités par le cylindre$x^2 + y^2 = 4$, respectivement.

Détermine le volume du solide$S_1$.
Détermine le volume du solide$S_2$.
Déterminez le volume du solide$S$ situé entre$S_1$ et$S_2$ en soustrayant les volumes des solides$S_1$ et$S_2$.

Réponse: a.$\frac{4}{3}\, \text{units}^3$
b.$2\pi\, \text{units}^3$
c.$\frac{6\pi - 4}{3}\, \text{units}^3$

50) [T] La figure suivante montre la région$D$ délimitée par les courbes$y = \sin x, \space x = 0$, et$y = x^4$. Utilisez un calculateur graphique ou un CAS pour trouver les$x$ coordonnées des points d'intersection des courbes et pour déterminer l'aire de la région$D$. Arrondissez vos réponses à la sixième décimale.

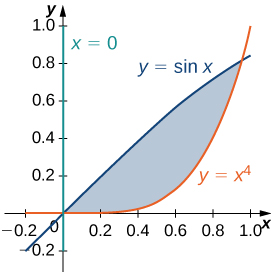
$Une région est délimitée par y = sin x, y = x jusqu'à la quatrième puissance et x = 0.$

51) [T] La région$D$ bounded by the curves $y = \cos x, \space x = 0$, and $y = x^3$ is shown in the following figure. Use a graphing calculator or CAS to find the $x$-coordinates of the intersection points of the curves and to determine the area of the region $D$. Round your answers to six decimal places.

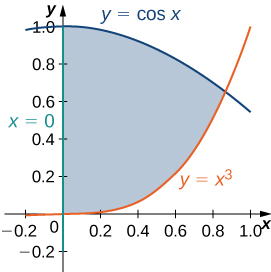
$A region is bounded by y = cos x, y = x cubed, and x = 0.$

Réponse: 0 et 0,865474 ;$A(D) = 0.621135\, \text{units}^3$

52) Supposons que ce$(X,Y)$ soit le résultat d'une expérience qui doit avoir lieu$S$ dans une région particulière du$xy$ plan. Dans ce contexte, la région$S$ est appelée espace d'échantillonnage de l'expérience$X$ et est constituée$Y$ de variables aléatoires. S'il s'$D$agit d'une région incluse dans$S$, alors la probabilité d'y$(X,Y)$ être$D$ est définie comme$P[(X,Y) \in D] = \iint_D p(x,y)dx \space dy$, où$p(x,y)$ est la densité de probabilité conjointe de l'expérience. $p(x,y)$Voici une fonction non négative pour laquelle$\iint_S p(x,y) dx \space dy = 1$. Supposons qu'un point$(X,Y)$ soit choisi arbitrairement dans le carré$[0,3] \times [0,3]$ avec la densité de probabilité

\[p(x,y) = \frac{1}{9} (x,y) \in [0,3] \times [0,3],\nonumber \]

\[p(x,y) = 0 \space \text{otherwise}\nonumber \]

Déterminez la probabilité que le point$(X,Y)$ se trouve à l'intérieur de l'unité carrée et interprétez le résultat.

53) Considérez$X$ et$Y$ deux variables aléatoires de densités de probabilité$p_1(x)$ et$p_2(x)$, respectivement. Les variables aléatoires$X$ et$Y$ sont dites indépendantes si leur fonction de densité conjointe est donnée par$p_(x,y) = p_1(x)p_2(y)$. Dans un restaurant au volant, les clients passent en moyenne 3 minutes à passer leurs commandes et 5 minutes supplémentaires à payer et à récupérer leurs repas. Supposons que passer la commande et paier/récupérer le repas sont deux événements indépendants$X$ et$Y$. Si les temps d'attente sont modélisés par les densités de probabilité exponentielles

\[p_1(x) = \frac{1}{3}e^{-x/3} \space x\geq 0,\nonumber \]

\[p_1(x) = 0 \space \text{otherwise}\nonumber \]

\[p_2(y) = \frac{1}{5} e^{-y/5} \space y \geq 0\nonumber \]

\[p_2(y) = 0 \space \text{otherwise}\nonumber \]

respectivement, la probabilité qu'un client passe moins de 6 minutes dans la file d'attente au volant est donnée par$P[X + Y \leq 6] = \iint_D p(x,y) dx \space dy$, où$D = {(x,y)|x \geq 0, \space y \geq 0, \space x + y \leq 6}$. Trouvez$P[X + Y \leq 6]$ et interprétez le résultat.

Réponse: $P[X + Y \leq 6] = 1 + \frac{3}{2e^2} - \frac{5}{e^{6/5}} \approx 0.45$; il est$45\%$ possible qu'un client passe$6$ quelques minutes dans la file d'attente au volant.

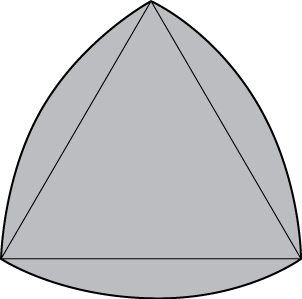
54) [T] Le triangle de Reuleaux est constitué d'un triangle équilatéral et de trois régions, chacune d'elles étant délimitée par un côté du triangle et un arc de cercle de rayon s centré au sommet opposé du triangle. Montrez que l'aire du triangle de Reuleaux dans la figure de longueur de côté suivante$s$ est$\frac{s^2}{2}(\pi - \sqrt{3})$.

$Triangle équilatéral avec des régions supplémentaires constituées de trois arcs de cercle dont le rayon est égal à la longueur du côté du triangle. Ces arcs relient deux sommets adjacents et le rayon provient du sommet opposé.$

55) [T] Montrez que l'aire des lunes d'Alhazen, les deux lunes bleues de la figure suivante, est la même que l'aire du triangle droit$ABC.$ The outer boundaries of the lunes are semicircles of diameters $AB$ and $AC$ respectively, and the inner boundaries are formed by the circumcircle of the triangle $ABC$.

$A right triangle with points A, B, and C. Point B has the right angle. There are two lunes drawn from A to B and from B to C with outer diameters AB and AC, respectively, and with the inner boundaries formed by the circumcircle of the triangle ABC.$