15.4 : Intégrales triples
- Page ID
- 197450
- Reconnaître lorsqu'une fonction de trois variables est intégrable sur une boîte rectangulaire.
- Évaluez une intégrale triple en l'exprimant sous la forme d'une intégrale itérée.
- Reconnaître quand une fonction de trois variables est intégrable sur une région fermée et délimitée.
- Simplifiez un calcul en modifiant l'ordre d'intégration d'une intégrale triple.
- Calculez la valeur moyenne d'une fonction de trois variables.
Nous avons discuté précédemment de la double intégrale d'une fonction\(f(x,y)\) de deux variables sur une région rectangulaire du plan. Dans cette section, nous définissons la triple intégrale d'une fonction\(f(x,y,z)\) de trois variables sur une boîte solide rectangulaire dans l'espace,\(\mathbb{R}^3\). Plus loin dans cette section, nous étendons la définition à des régions plus générales en\(\mathbb{R}^3\).
Fonctions intégrables de trois variables
Nous pouvons définir une boîte rectangulaire\(B\) en\(\mathbb{R}^3\) tant que
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber \]
Nous suivons une procédure similaire à celle que nous avons suivie précédemment. Nous divisons l'intervalle\([a,b]\) en\(l\) sous-intervalles\([x_{i-1},x_i]\) de même longueur\(\Delta x\) avec
\[\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber \]
divisez l'intervalle\([c,d]\) en\(m\) sous-intervalles\([y_{i-1}, y_i]\) de même longueur\(\Delta y\) avec
\[\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber \]
et divisez l'intervalle\([e,f]\) en\(n\) sous-intervalles\([z_{i-1},z_i]\) de même longueur\(\Delta z\) avec
\[\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber \]
Ensuite, la boîte rectangulaire\(B\) est subdivisée en\(lmn\) sous-cases :
\[B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber \]
comme le montre la figure\(\PageIndex{1}\).
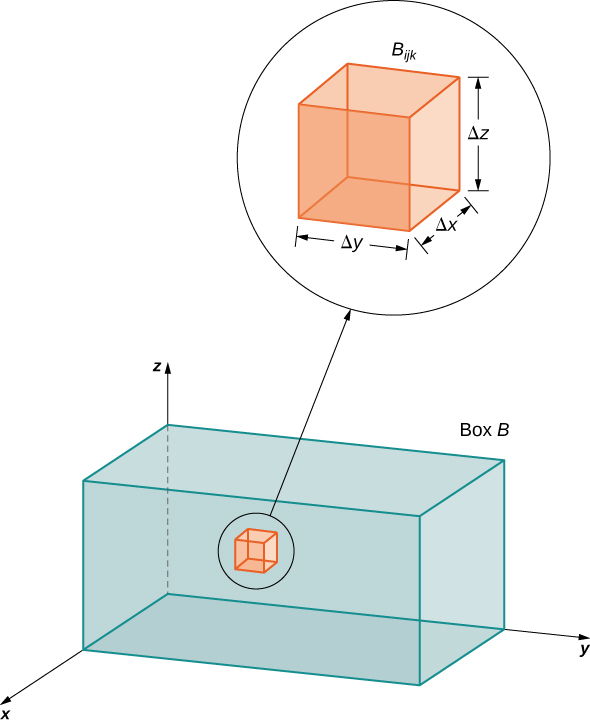
Pour chaque\(i, \, j,\) et\(k\), considérez un point d'échantillonnage\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) dans chaque sous-case\(B_{ijk}\). Nous voyons que son volume est\(\Delta V = \Delta x \Delta y \Delta z\). Formez la triple somme de Riemann
\[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber \]
Nous définissons l'intégrale triple en termes de limite d'une triple somme de Riemann, comme nous l'avons fait pour l'intégrale double en termes de double somme de Riemann.
L'intégrale triple d'une fonction\(f(x,y,z)\) sur une boîte rectangulaire\(B\) est définie comme
\[\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]si cette limite existe.
Lorsque la triple intégrale existe sur\(B\) la fonction, on dit qu'elle\(f(x,y,z)\) est intégrable sur\(B\). De plus, la triple intégrale existe si elle\(f(x,y,z)\) est continue\(B\). Par conséquent, nous utiliserons des fonctions continues pour nos exemples. Cependant, la continuité est suffisante mais pas nécessaire ; en d'autres termes, elle\(f\) est bornée\(B\) et continue, sauf éventuellement à la limite de\(B\). Le point d'échantillonnage\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) peut être n'importe quel point de la sous-boîte rectangulaire\(B_{ijk}\) et toutes les propriétés d'une intégrale double s'appliquent à une intégrale triple. Tout comme la double intégrale a de nombreuses applications pratiques, la triple intégrale a également de nombreuses applications, dont nous parlerons dans les sections suivantes.
Maintenant que nous avons développé le concept de la triple intégrale, nous devons savoir comment la calculer. Tout comme dans le cas de l'intégrale double, nous pouvons avoir une triple intégrale itérée, et par conséquent, il existe une version du théorème de Fubini pour les intégrales triples.
Si\(f(x,y,z)\) c'est continu sur une boîte rectangulaire\(B = [a,b] \times [c,d] \times [e,f]\), alors
\[\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber \]
Cette intégrale est également égale à n'importe lequel des cinq autres ordres possibles pour l'intégrale triple itérée.
Pour\(a, b, c, d, e\) et des nombres\(f\) réels, la triple intégrale itérée peut être exprimée dans six ordres différents :
\[\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber \]
Pour une boîte rectangulaire, l'ordre d'intégration ne fait pas de différence significative quant au niveau de difficulté du calcul. Nous calculons des intégrales triples en utilisant le théorème de Fubini plutôt que la définition de la somme de Riemann. Nous suivons l'ordre d'intégration de la même manière que pour les intégrales doubles (c'est-à-dire de l'intérieur vers l'extérieur).
Evaluer la triple intégrale\[\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber \]
Solution
L'ordre d'intégration est spécifié dans le problème, donc intégrez par rapport à d'\(x\)abord, puis à y et ensuite\(z\).
\[\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}\]
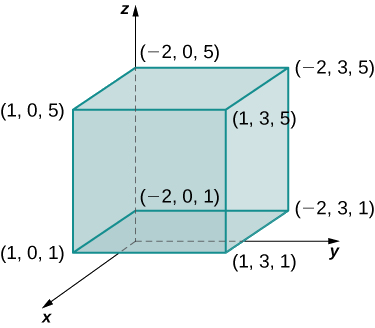
Évaluez la triple intégrale
\[\iiint_B x^2 yz \,dV \nonumber \]
où\(B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\} \), comme indiqué sur la figure\(\PageIndex{2}\).
Solution
L'ordre n'est pas spécifié, mais nous pouvons utiliser l'intégrale itérée dans n'importe quel ordre sans modifier le niveau de difficulté. Choisissez, par exemple, d'intégrer\(y\) d'abord, puis\(x\), et ensuite\(z\).
\[\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^3}{3} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{y}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = 162.\end{align*}\]
Maintenant, essayez d'intégrer dans un ordre différent pour obtenir la même réponse. Choisissez de procéder à l'intégration par rapport à\(x\) d'abord, puis\(z\), ensuite\(y\)
\[\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}\]
Évaluez la triple intégrale
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
où\(B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}\).
- Allusion
-
Suivez les étapes de l'exemple précédent.
- Réponse
-
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \]
Intégrale triple d'une fonction continue\(f(x,y,z)\) sur une région tridimensionnelle générale
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber \]
dans\(\mathbb{R}^3\), où\(D\) est la projection de\(E\) sur le\(xy\) plan -plane, est
\[\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber \]
De même, nous pouvons considérer une région délimitée générale\(D\) dans le\(xy\) plan -et deux fonctions\(y = u_1(x,z)\) et\(y = u_2(x,z)\) telle que\(u_1(x,z) \leq u_2(x,z)\) pour tous\((x,z)\) dedans\(D\). Ensuite, nous pouvons décrire la région solide\(E\) en\(\mathbb{R}^3\) tant que
\[E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber \]où\(D\) est la projection de\(E\) sur le\(xy\) plan -et la triple intégrale est
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber \]
Enfin, s'il s'\(D\)agit d'une région délimitée générale dans le\(xy\) plan -et que nous avons deux fonctions\(x = u_1(y,z)\),\(x = u_2(y,z)\) telles que\(u_1(y,z) \leq u_2(y,z)\) pour tout\((y,z)\) dedans\(D\), alors la région solide\(E\) dans\(\mathbb{R}^3\) peut être décrite comme
\[E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber \]où\(D\) est la projection de\(E\) sur le\(xy\) plan -et la triple intégrale est
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Notez que la région\(D\) de n'importe quel plan peut être de type I ou de type II, comme décrit précédemment. Si\(D\) le\(xy\) plan est de type I (Figure\(\PageIndex{4}\)), alors
\[E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
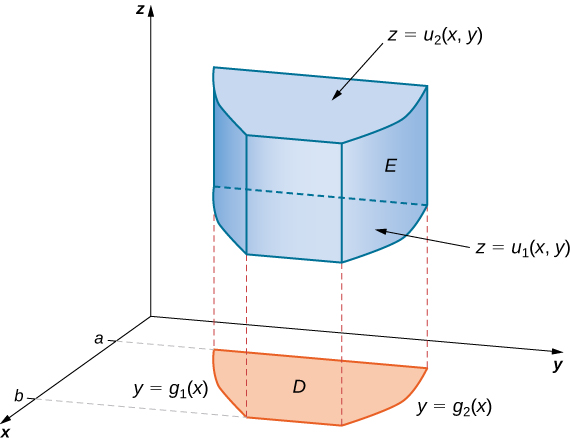
Ensuite, la triple intégrale devient
\[\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber \]
Si\(D\) le\(xy\) plan -est de type II (Figure\(\PageIndex{5}\)), alors
\[E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
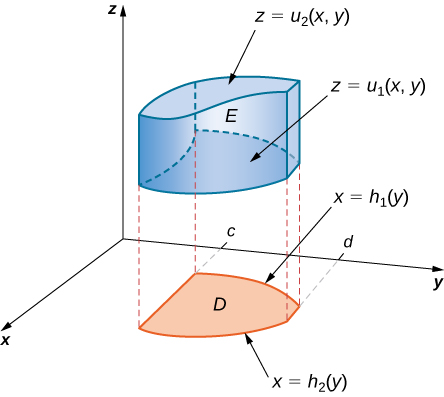
Ensuite, la triple intégrale devient
\[\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]
Évaluez la triple intégrale de la fonction\(f(x,y,z) = 5x - 3y\) sur le tétraèdre solide délimité par les plans\(x = 0, \, y = 0, \, z = 0\), et\(x + y + z = 1\).
Solution
La figure\(\PageIndex{6}\) montre le tétraèdre solide\(E\) et sa projection\(D\) sur le\(xy\) plan.
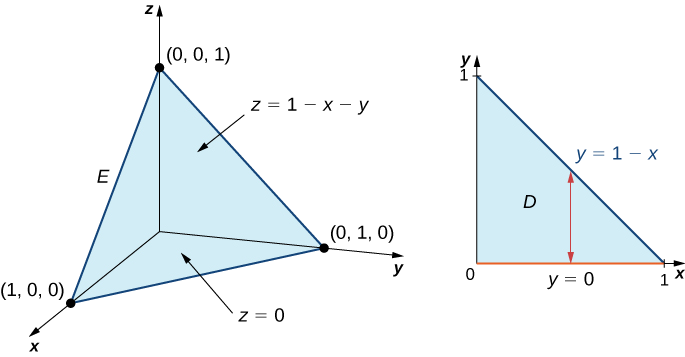
Nous pouvons décrire le tétraèdre à région solide comme
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber \]
Par conséquent, la triple intégrale est
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber \]
Pour simplifier le calcul, évaluez d'abord l'intégrale\(\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz\). Nous avons
\[\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber \]
Évaluez maintenant l'intégrale
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber \]
obtenant
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber \]
Enfin, évaluez
\[\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber \]
En rassemblant tout cela, nous avons
\[\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Tout comme nous avons utilisé la double intégrale\[\iint_D 1 \,dA \nonumber \] pour trouver l'aire d'une région délimitée générale,\(D\) nous pouvons l'utiliser\[\iiint_E 1\,dV \nonumber \] pour trouver le volume d'une région délimitée par un solide général\(E\). L'exemple suivant illustre la méthode.
Déterminez le volume d'une pyramide droite dont la base carrée se trouve dans le\(xy\) plan\([-1,1] \times [-1,1]\) et le sommet au point,\((0, 0, 1)\) comme indiqué dans la figure suivante.
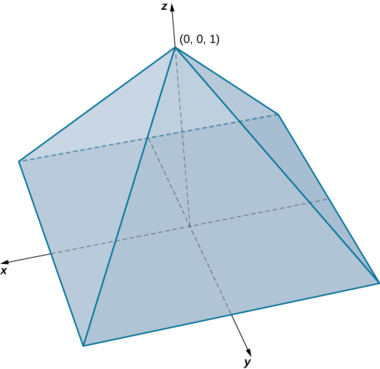
Solution
Dans cette pyramide, la valeur de\(z\) passe de 0 à 1 et, à chaque hauteur,\(z\) la section transversale de la pyramide pour toute valeur de\(z\) est le carré
\[[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber \]
Par conséquent, le volume de la pyramide est l'\[\iiint_E 1\,dV\nonumber \]endroit où
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber \]
Ainsi, nous avons
\ [\ begin {align*} \ IIInt_E 1 \, dV &= \ int_ {z=0} ^ {z=1} \ int_ {y=-1+z} ^ {y=1-z} \ int_ {x=-1+z} ^ {x=1-z} 1 \, dx \, dy \, dz \ \ [5 points]
&= \ int_ {z=0} 1 \, dx \, dy \, dz \ \ [5 points] &= \ int_ {z=0} ^ {z=1} \ int_ {y=-1+z} ^ {y=1-z} (2-2z) \, dy \, dz \ \ [5 points]
&= \ int_ {z=0} ^ {z=1} (2-2z) ^2 \, dz = \ dfrac {4} {3}. \ end {align*} \]
Le volume de la pyramide est donc exprimé en unités\(\dfrac{4}{3}\) cubiques.
Pensez à la sphère solide\(E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}\). Ecrivez l'intégrale triple\[\iiint_E f(x,y,z) \,dV\nonumber \] d'une fonction arbitraire\(f\) sous forme d'intégrale itérée. Évaluez ensuite cette triple intégrale avec\(f(x,y,z) = 1\). Notez que cela donne le volume d'une sphère en utilisant une triple intégrale.
- Allusion
-
Suivez les étapes de l'exemple précédent. Utilisez la symétrie.
- Réponse
-
\[\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}\]
Changer l'ordre de l'intégration
Comme nous l'avons déjà vu dans les intégrales doubles sur des régions délimitées générales, la modification de l'ordre de l'intégration est effectuée assez souvent pour simplifier le calcul. Avec une triple intégrale sur une boîte rectangulaire, l'ordre d'intégration ne modifie pas le niveau de difficulté du calcul. Cependant, avec une triple intégrale sur une région délimitée générale, le choix d'un ordre d'intégration approprié peut simplifier considérablement le calcul. Parfois, la modification des coordonnées polaires peut également être très utile. Nous présentons deux exemples ici.
Considérez l'intégrale itérée
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber \]
L'ordre d'intégration est ici d'abord par rapport à z, puis à y, puis à x. Exprimez cette intégrale en modifiant l'ordre d'intégration pour qu'il soit d'abord par rapport à\(x\)\(z\), ensuite et ensuite\(y\). Vérifiez que la valeur de l'intégrale est la même si nous le laissons faire\(f (x,y,z) =xyz\).
Solution
Le meilleur moyen d'y parvenir est d'esquisser la région\(E\) et ses projections sur chacun des trois plans de coordonnées. Ainsi, laissez
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber \]
et
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber \]
Nous devons exprimer cette triple intégrale comme
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber \]
Connaissant la région,\(E\) nous pouvons établir les projections suivantes (Figure\(\PageIndex{8}\)) :
sur le\(xy\) plan -est\(D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},\)
sur le\(yz\) plan -est\(D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}\), et
sur le\(xz\) plan -est\(D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}\).
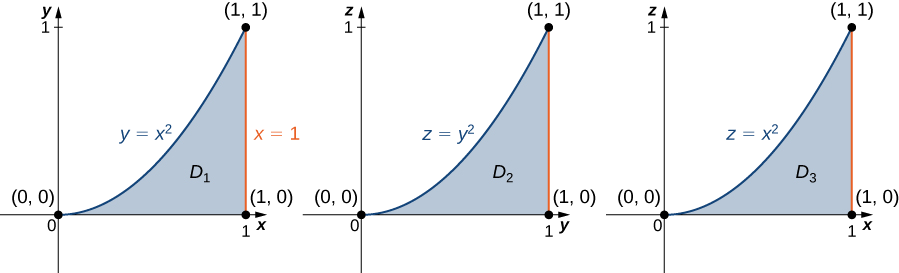
Nous pouvons maintenant décrire la même région\(E\) que\(\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}\), et par conséquent, la triple intégrale devient
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber \]
Supposons maintenant cela\(f (x,y,z) = xyz\) dans chacune des intégrales. Ensuite, nous avons
\ [\ begin {align*} \ int_ {x=0} ^ {x=1} \ int_ {y=0} ^ {y=x^2} \ int_ {z=0} ^ {z=y^2} xyz \, dz \, dy \, dx &= \ int_ {x=0} ^ {x=1} \ int_ {y=0} ^ {y=0} ^ {x=1} \ int_ {y=0} ^ {y=0} x^2} \ gauche. \ left [xy \ dfrac {z^2} {2} \ droite|_ {z=0} ^ {z=y^2} \ right] \, dy \, dx \ \ [5 points]
&= \ int_ {x=0} ^ {x=1} \ int_ {y=0} ^ {y=x^2} \ left (x \ dfrac {y^5} 2} \ right) dy \, dx \ \ [5 points]
&= \ int_ {x=0} ^ {x=1} \ gauche. \ left [x \ dfrac {y^6} {12} \ droite|_ {y=0} ^ {y=x^2} \ right] dx \ \ [5 points]
&= \ int_ {x=0} ^ {x=1} \ dfrac {x^ {13}} {12} dx = \ left. \ dfrac {x^ {14}} {168} \ right|_ {x=0} ^ {x=1} \ \ [5 points]
&= \ dfrac {1} {168}, \ end {align*} \]
\ [\ begin {align*} \ int_ {y=0} ^ {y=1} \ int_ {z=0} ^ {z=y^2} \ int_ {x= \ sqrt {y}} ^ {x=1} xyz \, dx \, dz \, dy &= \ int_ {y=0} ^ {y=1} \ int_ {z=0} ^ {y=1} \ int_ {z=0} ^ {z=y^2} \ gauche. \ left [yz \ dfrac {x^2} {2} \ droite|_ {\ sqrt {y}} ^ {1} \ right] dz \, dy \ \ [5 points]
&= \ int_ {y=0} ^ {y=1} \ int_ {z=0} ^ {z=y^2} \ left (\ dfrac {yz} {2} - dfrac {y^2z} {2} \ (droite) dz \, dy \ \ [5 points]
&= \ int_ {y=0} ^ {y=1} \ gauche. \ left [\ dfrac {yz^2} {4} - \ dfrac {y^2z^2} {4} \ droite|_ {z=0} ^ {z=y^2} \ droite] dy \ \ [5 points]
&= \ int_ {y=0} ^ {y=1} \ left (\ dfrac {y^5} {4} - \ dfrac {y^6} {4} \ (droite) dy \ \ [5 points]
&= \ gauche. \ left (\ dfrac {y^6} {24} - \ dfrac {y^7} {28} \ right) \ droite|_ {y=0} ^ {y=1} \ \ [5 points]
&= \ dfrac {1} {168}. \ end {align*} \ nonumber \]
Les réponses correspondent.
Écrivez cinq intégrales itérées différentes égales à l'intégrale donnée
\[\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber \]
- Allusion
-
Suivez les étapes de l'exemple précédent, en utilisant la région\(E\) comme\( \big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}\), puis décrivez et esquissez les projections sur chacun des trois plans, cinq fois différentes.
- Réponse
-
\[(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber \]
\[ (iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber \]
Évaluez la triple intégrale
\[\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber \]
où\(E\) est la région délimitée par le paraboloïde\(y = x^2 + z^2\) (Figure\(\PageIndex{9}\)) et le plan\(y = 4\).
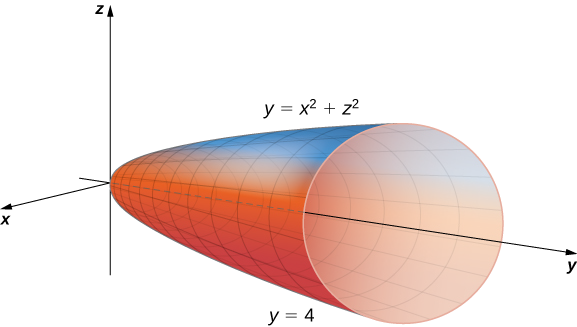
Solution
La projection de la région solide\(E\) sur le\(xy\) plan est la région délimitée au-dessus\(y = 4\) et en dessous par la parabole,\(y = x^2\) comme indiqué.
Ainsi, nous avons
\[E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \sqrt{y - x^2} \big\}.\nonumber \]
La triple intégrale devient
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber \]
Cette expression est difficile à calculer, alors considérez la\(E\) projection de sur le\(xz\) plan. Il s'agit d'un disque circulaire\(x^2 + z^2 \leq 4\). Nous obtenons donc
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber \]
Ici, l'ordre d'intégration passe d'abord par rapport à\(z\) ensuite,\(y\) puis\(x\) à être premier par rapport à\(y\) ensuite\(z\) et ensuite à\(x\). Il sera bientôt clair en quoi ce changement peut être bénéfique pour le calcul. Nous avons
\[\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber \]
Utilisez maintenant la substitution polaire\(x = r \, \cos \, \theta, \, z = r \, \sin \, \theta\), et\(dz \, dx = r \, dr \, d\theta\) dans le\(xz\) plan. C'est essentiellement la même chose que lorsque nous utilisions des coordonnées polaires dans le\(xy\) plan, sauf que nous les remplaçons\(y\) par\(z\). Par conséquent, les limites de l'intégration changent et nous avons, en utilisant\(r^2 = x^2 + z^2\),
\[\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Valeur moyenne d'une fonction à trois variables
Rappelons que nous avons trouvé la valeur moyenne d'une fonction de deux variables en évaluant l'intégrale double sur une région du plan, puis en divisant par l'aire de la région. De même, nous pouvons trouver la valeur moyenne d'une fonction dans trois variables en évaluant l'intégrale triple sur une région solide, puis en divisant par le volume du solide.
Si elle\(f(x,y,z)\) est intégrable sur une région délimitée solide\(E\) avec un volume positif\(V \, (E),\), alors la valeur moyenne de la fonction est
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber \]
Notez que le volume est
\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
La température en un point\((x,y,z)\) d'un solide\(E\) délimité par les plans de coordonnées et le plan\(x + y + z = 1\) est\(T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C} \). Détermine la température moyenne au-dessus du solide.
Solution
Utilisez le théorème ci-dessus et la triple intégrale pour trouver le numérateur et le dénominateur. Ensuite, faites la division. Remarquez que l'avion\(x + y + z = 1\) a des interceptions\((1,0,0), \, (0,1,0),\) et\((0,0,1)\). La région\(E\) ressemble à
\[E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber \]
Ainsi, la triple intégrale de la température est
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber \]
L'évaluation du volume est
\[V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
Par conséquent, la valeur moyenne est
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber \].
Détermine la valeur moyenne de la fonction\(f(x,y,z) = xyz\) sur le cube dont les côtés ont une longueur de 4 unités dans le premier octant avec un sommet à l'origine et des arêtes parallèles aux axes de coordonnées.
- Allusion
-
Suivez les étapes de l'exemple précédent.
- Réponse
-
\(f_{ave} = 8\)
Concepts clés
- Pour calculer une triple intégrale, nous utilisons le théorème de Fubini, qui indique que si elle\(f(x,y,z)\) est continue sur une boîte rectangulaire\(B = [a,b] \times [c,d] \times [e,f]\), alors\[\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber \] et est également égale à n'importe lequel des cinq autres ordres possibles pour la triple intégrale itérée.
- Pour calculer le volume d'une région délimitée par un solide général,\(E\) nous utilisons la triple intégrale\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
- L'échange de l'ordre des intégrales itérées ne change pas la réponse. En fait, l'échange de l'ordre d'intégration peut contribuer à simplifier le calcul.
- Pour calculer la valeur moyenne d'une fonction sur une région tridimensionnelle générale, nous utilisons\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Équations clés
- Intégrale triple
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]
Lexique
- triple intégrale
- l'intégrale triple d'une fonction continue\(f(x,y,z)\) sur une boîte pleine rectangulaire\(B\) est la limite d'une somme de Riemann pour une fonction de trois variables, si cette limite existe



Intégrales triples sur une région délimitée par des limites générales
Nous étendons maintenant la définition de la triple intégrale pour calculer une triple intégrale sur une région bornée plus générale\(E\) dans\(\mathbb{R}^3\). Les régions délimitées générales que nous allons examiner sont de trois types. Tout d'abord,\(D\) soit la région délimitée qui est une\(E\) projection sur le\(xy\) plan. Supposons que la région\(E\) dans se\(\mathbb{R}^3\) présente sous la forme
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
Pour deux fonctions\(z = u_1(x,y)\) et\(u_2(x,y)\), de telle sorte que\(u_1(x,y) \leq u_2(x,y)\) pour tous\((x,y)\),\(D\) comme indiqué dans la figure suivante.