15.1 : Intégrales doubles sur des régions rectangulaires

Objectifs d'apprentissage

• Reconnaître quand une fonction de deux variables est intégrable sur une région rectangulaire.
• Reconnaissez et utilisez certaines propriétés des intégrales doubles.
• Evaluez une intégrale double sur une région rectangulaire en l'écrivant comme une intégrale itérée.
• Utilisez une intégrale double pour calculer l'aire d'une région, le volume sous une surface ou la valeur moyenne d'une fonction sur une région plane.

Dans cette section, nous étudions les intégrales doubles et montrons comment les utiliser pour déterminer le volume d'un solide sur une région rectangulaire du plan xy. De nombreuses propriétés des intégrales doubles sont similaires à celles que nous avons déjà discutées pour les intégrales simples.

Volumes et intégrales doubles

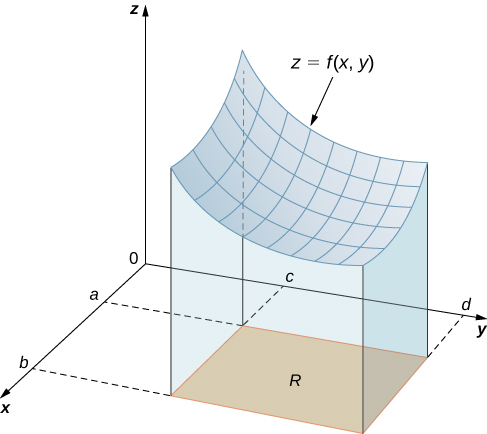
Nous commençons par considérer l'espace au-dessus d'une région rectangulaire\(R\). Considérons une fonction continue\(f(x,y)≥0\) de deux variables définies sur le rectangle fermé\(R\) :

\[R=[a,b] \times [c,d]= \left\{(x,y) ∈ \mathbb{R}^2| \, a ≤ x ≤ b, \, c ≤ y ≤ d \right\} \nonumber \]

\([a,b] \times [c,d]\)On désigne ici le produit cartésien des deux intervalles fermés\([a,b]\) et\([c,d]\). Il se compose de paires rectangulaires\((x,y)\) telles que\(a≤x≤b\) et\(c≤y≤d\). Le graphique de\(f\) représente une surface au-dessus du\(xy\) plan avec l'équation\(z = f(x,y)\) où\(z\) est la hauteur de la surface au point\((x,y)\). \(S\)Soit le solide qui se trouve au-dessus\(R\) et en dessous du graphique de\(f\) (Figure\(\PageIndex{1}\)). La base du solide est le rectangle\(R\) dans le\(xy\) plan. Nous voulons connaître le volume\(V\) du solide\(S\).

Figure\(\PageIndex{1}\) : Le graphique du\(f(x,y)\) dessus du rectangle R dans le\(xy\) plan est une surface incurvée.

Nous divisons la région\(R\) en petits rectangles\(R_{ij}\), chacun avec une surface\(ΔA\) et des côtés\(Δx\) et\(Δy\) (Figure\(\PageIndex{2}\)). Pour ce faire, nous divisons l'intervalle\([a,b]\) en\(m\) sous-intervalles et en divisant l'intervalle\([c,d]\) en\(n\) sous-intervalles. Par\(\Delta x = \frac{b - a}{m}\) conséquent\(\Delta y = \frac{d - c}{n}\), et\(\Delta A = \Delta x \Delta y\).

Figure\(\PageIndex{2}\) :\(R\) Le rectangle est divisé en petits rectangles ayant\(R_{ij}\) chacun une surface\(\Delta A\).

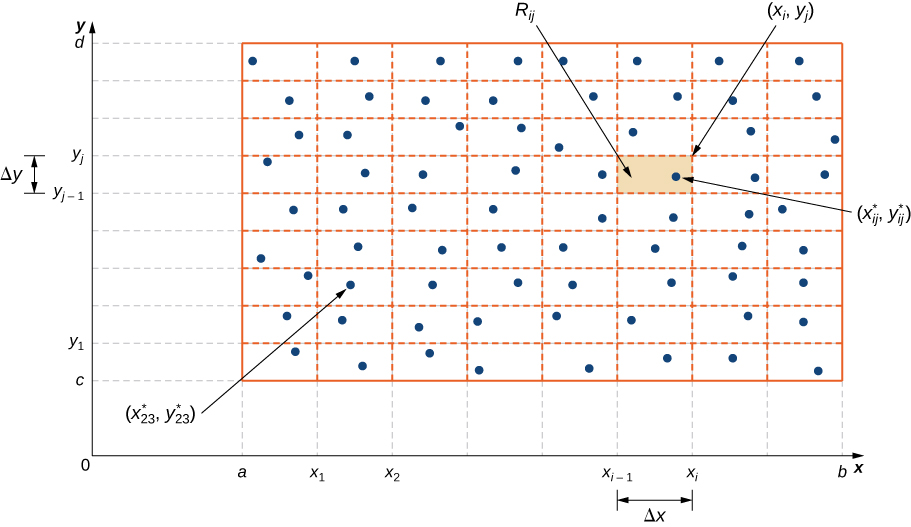
Le volume d'une fine boîte rectangulaire ci-dessus\(R_{ij}\) est\(f(x_{ij}^*, \, y_{ij}^*)\,\Delta A\), où (\(x_{ij}^*, \, y_{ij}^*\)) est un point d'échantillonnage arbitraire dans chacune d'elles,\(R_{ij}\) comme indiqué dans la figure suivante,\(f(x_{ij}^*, \, y_{ij}^*)\) est la hauteur de la boîte rectangulaire mince correspondante et\(\Delta A\) est la surface de chaque rectangle\(R_{ij}\).

Figure\(\PageIndex{3}\) : Une fine boîte rectangulaire surmontée\(R_{ij}\) d'une hauteur\(f(x_{ij}^*, \, y_{ij}^*)\).

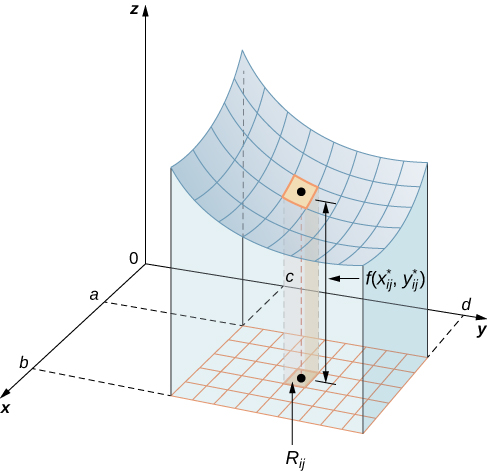
En utilisant la même idée pour tous les sous-rectangles, nous obtenons un volume approximatif du solide S comme

\[V \approx \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]

Cette somme est connue sous le nom de double somme de Riemann et peut être utilisée pour approximer la valeur du volume du solide. Ici, la double somme signifie que pour chaque sous-rectangle, nous évaluons la fonction au point choisi, la multiplions par l'aire de chaque rectangle, puis nous ajoutons tous les résultats.

Comme nous l'avons vu dans le cas d'une variable unique, nous obtenons une meilleure approximation du volume réel si\(m\)\(n\) celui-ci augmente.

\[V = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*) \Delta A \nonumber \]

ou

\[V=\lim_{\Delta x, \, \Delta y \rightarrow 0} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]

Notez que la somme se rapproche d'une limite dans les deux cas et que la limite est le volume du solide avec la base\(R\). Nous sommes maintenant prêts à définir la double intégrale.

Définition : Intégrale double sur une région rectangulaire R

La double intégrale de la fonction\(f(x, \, y)\) sur la\(R\) région rectangulaire du\(xy\) plan -est définie comme

\[\iint_R f(x, \, y) dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]

Si\(f(x,y)\geq 0\), then the volume \(V\) of the solid \(S\), which lies above \(R\) in the \(xy\)-plane and under the graph of \(f\), is the double integral of the function \(f(x,y)\) over the rectangle \(R\). If the function is ever negative, then the double integral can be considered a “signed” volume in a manner similar to the way we defined net signed area in l'intégrale définie.

Exemple\(\PageIndex{1}\): Setting up a Double Integral and Approximating It by Double Sums

Considérez la fonction\(z = f(x, \, y) = 3x^2 - y\) sur la région rectangulaire\(R = [0, 2] \times [0, 2]\) (Figure\(\PageIndex{4}\)).

1. Définissez une intégrale double pour trouver la valeur du volume signé du solide\(S\) situé au-dessus\(R\) et « sous » le graphique de\(f\).
2. Divisez\(R\) en quatre carrés avec\(m = n = 2\) et choisissez le point d'échantillonnage comme point d'angle supérieur droit de chaque carré (1,1), (2,1), (1,2) et (2,2) (Figure\(\PageIndex{4}\)) pour obtenir une approximation du volume signé du solide\(S\) situé au-dessus\(R\) et « sous » le graphique de\(f\).
3. Divisez\(R\) en quatre carrés et choisissez le point d'échantillonnage comme point médian de chaque carré : (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) et (3/2, 3/2) pour obtenir une approximation du volume signé.\(m = n = 2\)

   

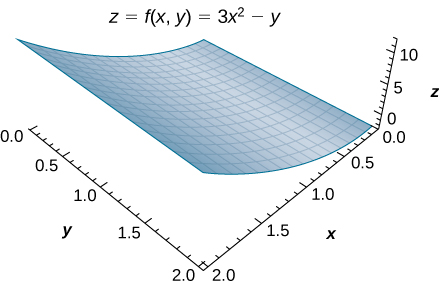
   Figure\(\PageIndex{4}\) : La fonction\(z=f(x,y)\) est représentée graphiquement sur la région rectangulaire\(R=[0,2]×[0,2]\).

Solution

1. Comme on peut le voir, la fonction\(z = f(x,y) = 3x^2 - y\) se trouve au-dessus du plan. Pour trouver le volume signé de\(S\), nous devons diviser la région\(R\) en petits rectangles\(R_{ij}\), chacun avec une surface\(ΔA\) et des côtés et\(Δy\),\(Δx\) et choisir\((x_{ij}^*, y_{ij}^*)\) comme points d'échantillonnage dans chacun d'eux\(R_{ij}\). Par conséquent, une double intégrale est définie comme

   \[V = \iint_R (3x^2 - y) dA = \lim_{m,n→∞} \sum_{i=1}^m \sum_{j=1}^n [3(x_{ij}^*)^2 - y_{ij}^*] \Delta A. \nonumber \]

2. En approximant le volume signé à l'aide d'une somme de Riemann,\(m = n = 2\) nous avons\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). De plus, les points d'échantillonnage sont (1, 1), (2, 1), (1, 2) et (2, 2), comme indiqué dans la figure suivante.

Figure\(\PageIndex{5}\) : Sous-rectangles pour la région rectangulaire\(R=[0,2]×[0,2]\).

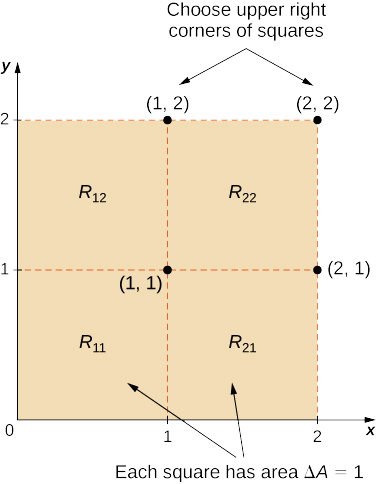
Par conséquent,

\ [\ begin {align*} V & \ approx \ sum_ {i=1} ^2 \ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*) \ Delta A \ \ [4 points]
&= \ sum_ {i=1} ^2 (f (x_ {i1} ^*, y_ {i1} ^*) + (f (x_ {i1} ^*) (f (x_ {i1} ^*) x_ {i2} ^*, y_ {i2} ^*)) \ Delta A \ \ [4 points]
&=f (x_ {11} ^*, y_ {11} ^*) \ Delta A + f (x_ {21} ^*, y_ {21} ^*) \ Delta A + f (x_ {12} ^*, y_ {12} ^*) \ Delta A + f (x_ {22} ^*, y_ {22} ^*) \ Delta A \ \ [4 points]
&= f (1,1) (1) + f (2,1) (1) + f (1,2) (1) + f (2,2) (1) \ \ [4 points]
&= (3 - 1) (1) + (12 - 1) + (1) + (3 - 2) (1) (12 - 2) (1) \ \ [4 points]
&= 2 + 11 + 1 + 10 = 24. \ end {align*} \]

3. En approximant le volume signé à l'aide d'une somme de Riemann,\(m = n = 2\) nous avons\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). Dans ce cas, les points d'échantillonnage sont (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) et (3/2, 3/2).
   Par conséquent,
    \ [\ begin {align*} V & \ approx \ sum_ {i=1} ^2 \ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*) \ Delta A \ \ [4pt]
   &=f (x_ {11} ^*, y_ {11} ^*) \ Delta A + f (x_ {21} ^*) \ Delta A + f (x_ {21} ^*, y_ {21} ^*) \ Delta A + f (x_ {12} ^*, y_ {12} ^*) \ Delta A + f (x_ {22} ^*, y_ {22} ^*) \ Delta A \ \ [4 points]
   &= f (1/2,1/2) (1) + f (3/2,1/2) (1) + f (1/2,3/2) (1) + f (3/2,3/2) (1) \ \ [4 points]
   &= \ left (\ frac {3} {4}} - \ frac {1} {4} \ droite) (1) + \ left (\ frac {27} {4} - \ frac ac {1} {2} \ droite) (1) + \ gauche (\ frac {3} {4} - \ frac {3} {2} \ droite) (1) + \ gauche (\ frac {27} {4} - \ frac {3} {2} \ droite) (1) \ \ [4 points]
   &= \ frac {2} {4} + \ frac {25} {4} + \ left (- \ frac {3} {4} \ right) + \ frac {21} {4} = \ frac {45} {4} = 11. \ end {align*} \]

Analyse

Notez que les réponses approximatives diffèrent en raison du choix des points d'échantillonnage. Dans les deux cas, nous introduisons une erreur parce que nous n'utilisons que quelques points d'échantillonnage. Nous devons donc étudier comment nous pouvons obtenir une réponse précise.

Exercice\(\PageIndex{1}\)

Utilisez la même fonction\(z = f(x, y) = 3x^2 - y\) sur la région rectangulaire\(R=[0,2]×[0,2]\).

Divisez\(R\) en quatre carrés identiques et choisissez les points d'échantillonnage comme point dans le coin supérieur gauche de chaque carré (0,1), (1,1), (0,2) et (1,2) (Figure\(\PageIndex{5}\)) pour obtenir une approximation du volume signé du solide\(S\) situé au-dessus\(R\) et « sous » le graphique de\(f\).\(m = n = 2\)

Allusion

Suivez les étapes de l'exemple précédent.

Réponse

\[V \approx \sum_{i=1}^2 \sum_{j=1}^2 f(x_{ij}^*, y_{ij}^*)\,\Delta A = 0 \nonumber \]

Notez que nous avons développé le concept de double intégrale en utilisant une région rectangulaire\(R\). Ce concept peut être étendu à n'importe quelle région générale. Toutefois, lorsqu'une région n'est pas rectangulaire, les sous-rectangles peuvent ne pas tous s'intégrer parfaitement\(R\), en particulier si la zone de base est incurvée. Nous examinons cette situation plus en détail dans la section suivante, où nous étudions des régions qui ne sont pas toujours rectangulaires et où les sous-rectangles peuvent ne pas s'adapter parfaitement à la région\(R\). De plus, les hauteurs peuvent ne pas être exactes si la surface\(z=f(x,y)\) est incurvée. Cependant, les erreurs sur les côtés et sur la hauteur où les pièces peuvent ne pas s'ajuster parfaitement dans le solide\(S\) approchent de 0\(m\) et s'\(n\)approchent de l'infini. De plus, la double intégrale de la fonction\(z=f(x,y)\) existe à condition que la fonction ne\(f\) soit pas trop discontinue. Si la fonction est bornée et continue\(R\) sauf sur un nombre fini de courbes lisses, alors la double intégrale existe et nous disons que ff est intégrable\(R\).

Depuis\(\Delta A = \Delta x \Delta y = \Delta y \Delta x\), nous pouvons exprimer\(dA\) comme\(dx \, dy\) ou\(dy \, dx\). Cela signifie que, lorsque nous utilisons des coordonnées rectangulaires, la double intégrale sur une région\(R\) désignée par

\[\iint_R f(x,y)\,dA \nonumber \]

peut être écrit comme

\[\iint_R f(x,y)\,dx\,dy \nonumber \]

ou

\[\iint_R f(x,y)\,dy\,dx. \nonumber \]

Nous allons maintenant énumérer certaines des propriétés qui peuvent être utiles pour calculer des intégrales doubles.

Propriétés des intégrales doubles

Les propriétés des intégrales doubles sont très utiles lors de leur calcul ou de leur utilisation. Nous listons ici six propriétés des intégrales doubles. Les propriétés 1 et 2 sont appelées la linéarité de l'intégrale, la propriété 3 est l'additivité de l'intégrale, la propriété 4 est la monotonicité de l'intégrale et la propriété 5 est utilisée pour déterminer les limites de l'intégrale. La propriété 6 est utilisée si elle\(f(x,y)\) est le produit de deux fonctions\(g(x)\) et\(h(y)\).

Théorème : Propriétés des intégrales doubles

Supposons que les fonctions\(f(x,y)\) et\(g(x,y)\) soient intégrables sur la région rectangulaire\(R\) ;\(S\) et qu'\(T\)elles soient des sous-régions de\(R\) ; et supposons que ce\(m\)\(M\) sont des nombres réels.

1. La somme\(f(x,y)+g(x,y)\) est intégrable et

\[\iint_R [f(x, y) + g(x, y)]\,dA = \iint_R f(x,y)\, dA + \iint_R g(x, y) \,dA. \nonumber \]

2. Si c est une constante, alors\(cf(x,y)\) est intégrable et

\[\iint_R cf(x,y)\,dA = c\iint_R f(x,y)\,dA. \nonumber \]

3. Si\(R=S∪T\) et\(S∩T=∅\) sauf un chevauchement des limites, alors

\[\iint_R f(x,y)\,dA = \iint_S f(x,y) \,dA + \iint_T f(x,y)\, dA. \nonumber \]

4. Si\(f(x,y) \geq g(x,y)\) c'\((x,y)\)est pour\(R\), alors

\[\iint_R f(x,y)\,dA \geq \iint_R g(x,y)\,dA. \nonumber \]

5. Si\(m \leq f(x,y) \leq M\) et\(A(R) = \, \text{the area of}\,R\), alors

\[m \cdot A(R) \leq \iint_R f(x,y)\,dA \leq M \cdot A(R). \nonumber \]

6. Dans le cas où\(f(x,y)\) peut être prise en compte comme le produit d'une fonction\(g(x)\) de\(x\) uniquement et d'une fonction\(h(y)\) de\(y\) uniquement, alors sur la région\(R = \big\{(x,y) \,|\,a \leq x \leq b, \, c \leq y \leq d \big\}\), la double intégrale peut être écrite comme

\[\iint_R f(x,y)\,dA = \left(\int_a^b g(x)\,dx \right)\left(\int_c^d h(y) \,dy \right). \nonumber \]

Ces propriétés sont utilisées dans l'évaluation des intégrales doubles, comme nous le verrons plus loin. Nous apprendrons à utiliser ces propriétés une fois que nous serons familiarisés avec les outils de calcul des intégrales doubles. Alors, allons-y maintenant.

Intégrales itérées

Jusqu'à présent, nous avons vu comment configurer une double intégrale et comment obtenir une valeur approximative pour celle-ci. Nous pouvons également imaginer que l'évaluation des intégrales doubles à l'aide de la définition peut être un processus très long si nous choisissons des valeurs plus grandes pour\(m\) et\(n\). Par conséquent, nous avons besoin d'une technique pratique et pratique pour calculer les intégrales doubles. En d'autres termes, nous devons apprendre à calculer des intégrales doubles sans utiliser la définition qui utilise des limites et des doubles sommes.

L'idée de base est que l'évaluation devient plus facile si nous pouvons diviser une intégrale double en intégrales simples en intégrant d'abord par rapport à une variable, puis par rapport à l'autre. L'outil clé dont nous avons besoin s'appelle une intégrale itérée.

Définitions : Intégrales itérées

Supposons que\(a\)\(b\)\(c\), et\(d\) soient des nombres réels. Nous définissons une intégrale itérée pour une fonction\(f(x,y)\) sur la région rectangulaire\(R =[a,b]×[c,d]\) comme

\[\int_a^b\int_c^d f(x,y)\,dy \, dx = \int_a^b \left[\int_c^d f(x,y)\,dy \right] dx \nonumber \]

ou

\[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d \left[\int_a^b f(x,y)\,dx \right] dy. \nonumber \]

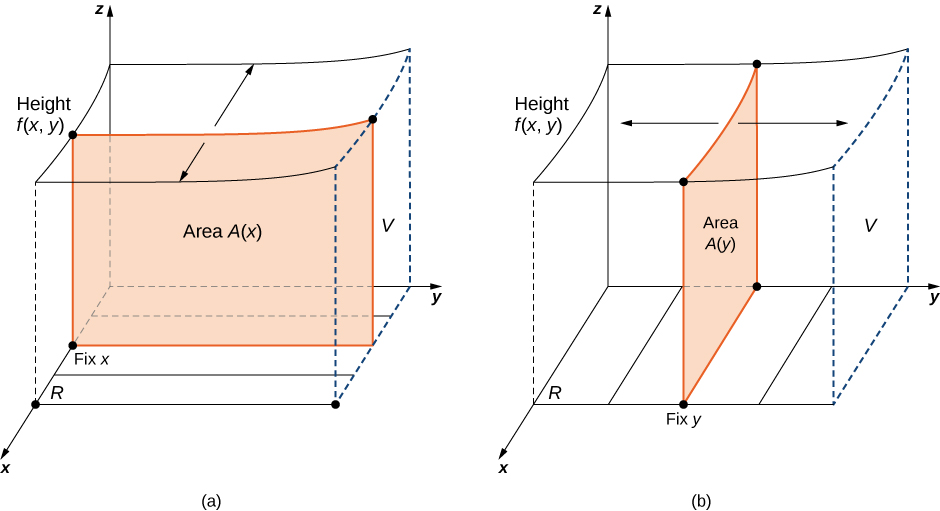
La notation\(\int_a^b \left[\int_c^d f(x,y)\,dy \right] dx\) signifie que nous intégrons\(f(x,y)\) par rapport à\(y\) tout en maintenant\(x\) une constante. De même, la notation\(\int_c^d \left[\int_a^b f(x,y)\,dx \right] dy\) signifie que nous intégrons\(f(x,y)\) par rapport à\(x\) tout en maintenant\(y\) une constante. Le fait que les intégrales doubles puissent être divisées en intégrales itérées est exprimé dans le théorème de Fubini. Considérez ce théorème comme un outil essentiel pour évaluer les intégrales doubles.

Théorème : Théorème de Fubini

Supposons que\(f(x,y)\) c'est une fonction de deux variables qui est continue sur une région rectangulaire\(R = \big\{(x,y) ∈ \mathbb{R}^2 | \, a \leq x \leq b, \, c \leq y \leq d \big\}\). Ensuite, nous voyons sur la figure\(\PageIndex{6}\) que la double intégrale de\(f\) sur la région est égale à une intégrale itérée,

\[\iint_R f(x,y)\,dA = \iint_R f(x,y)\,dx \, dy = \int_a^b \int_c^d f(x,y)\,dy \, dx = \int_c^d \int_a^b f(x,y)\,dx \, dy. \nonumber \]

Plus généralement, le théorème de Fubini\(f\) est vrai s'il\(f\) est limité\(R\) et discontinu uniquement sur un nombre fini de courbes continues. En d'autres termes,\(f\) doit être intégrable\(R\).

Figure\(\PageIndex{6}\) : (a) Intégration d'abord par rapport à,\(y\) puis par rapport\(x\) à pour trouver la zone,\(A(x)\) puis le volume\(V\) ; (b) intégration d'abord par rapport à,\(x\) puis par rapport\(y\) à pour trouver la zone,\(A(y)\) puis le volume \(V\).

Exemple\(\PageIndex{2}\): Using Fubini’s Theorem

Utilisez le théorème de Fubini pour calculer la double intégrale\(\displaystyle \iint_R f(x,y) \,dA\) où\(f(x,y) = x\) et\(R = [0, 2] \times [0, 1]\).

Solution

Le théorème de Fubini offre un moyen plus simple d'évaluer l'intégrale double en utilisant une intégrale itérée. Notez comment les valeurs limites de la région\(R\) deviennent les limites supérieure et inférieure de l'intégration.

\ [\ begin {align*} \ IInt_r f (x, y) \, dA &= \ IInt_R f (x, y) \, dx \, dy \ \ [4 points]
&= \ int_ {y=0} ^ {y=1} \ int_ {x=0} ^ {x=2} x \, dx \, dy \ \ [4 points]
&= int_ {y=0} ^ {y=1} \ left [\ frac {x^2} {2} \ bigg|_ {x=0} ^ {x=2} \ droite] \, dy \ \ [4 points]
&= \ int_ {y=0} ^ {y=1} 2 \, dy = 2 ans \ bigg|_ {y=0 } ^ {y=1} = 2 \ end {align*} \]

La double intégration dans cet exemple est suffisamment simple pour utiliser directement le théorème de Fubini, ce qui nous permet de convertir une intégrale double en une intégrale itérée. Par conséquent, nous sommes maintenant prêts à convertir toutes les intégrales doubles en intégrales itérées et à démontrer comment les propriétés répertoriées précédemment peuvent nous aider à évaluer les intégrales doubles lorsque la fonction\(f(x,y)\) est plus complexe. Notez que l'ordre d'intégration peut être modifié (voir Exemple 7).

Exemple\(\PageIndex{3}\): Illustrating Properties i and ii

Evaluer la double intégrale\[\iint_R (xy - 3xy^2) \,dA, \, \text{where} \, R = \big\{(x,y) \,| \, 0 \leq x \leq 2, \, 1 \leq y \leq 2 \big\}.\nonumber \]

Solution

Cette fonction comporte deux éléments : l'un est\(xy\) et l'autre l'est\(3xy^2\). De plus, la deuxième pièce a une constante 3. Remarquez comment nous utilisons les propriétés i et ii pour évaluer la double intégrale.

\ [\ begin {align*} \ IInt_R (xy - 3xy^2) \, dA &= \ iInt_R xy \, dA + \ iInt_R (-3xy^2) \, dA & & & \ text {Propriété i : L'intégrale d'une somme est la somme des intégrales.} \ \ [4pt]
&= \ int_ {y=1} ^ {y=2} \ int_ {x=0} ^ {x=2} xy \, dx \, dy - \ int_ {y=1} ^ {y=2} \ int_ {x=0} ^ {x=2} 3xy^2 \, dx \, dy & & \ text {Convertir des intégrales doubles en intégrales itérées.} \ \ [4pt]
&= \ int_ {y=1} ^ {y=2} \ left (\ frac {x^2} {2} y \ right) \ bigg|_ {x=0} ^ {x=2} \, dy - 3 \ int_ {y=1} ^ {y=2} \ left (\ {frac x^2} {2} y^2 \ right) \ bigg|_ {x=0} ^ {x=2} \, dy & & \ text {Intégrez par rapport à $x$, en maintenant $y$ constant.} \ \ [4pt]
&= \ int_ {y=1} ^ {y=2} 2y \, dy - \ int_ {y=1} ^ {y=2} 6y^2 dy & & \ text {Propriété ii : Placer la constante avant l'intégrale.} \ \ [4pt]
&= 2 \ int_1^2 y \, dy - 6 \ int_1^2 y^2 \, dy & & \ text {Intégrer avec par rapport à y.} \ \ [4pt]
&= 2 \ frac {y^2} {2} \ bigg|_1^2 - 6 \ frac {y^3} {3} \ bigg|_1^2 \ \ [4 points]
&=y^2 \ bigg|_1^2 - 2y^3 \ bigg|_1^2 \ \ [4 points]
& =( 4−1) − 2 (8−1) = 3 − 2 (7) = 3 − 14 = −11. \ end {align*} \]

Exemple\(\PageIndex{4}\): Illustrating Property v.

Dans toute la région\(R = \big\{(x,y)\,| \, 1 \leq x \leq 3, \, 1 \leq y \leq 2 \big\}\), nous avons\(2 \leq x^2 + y^2 \leq 13\). Trouvez une limite inférieure et une limite supérieure pour l'intégrale\(\displaystyle \iint_R (x^2 + y^2)\,dA.\)

Solution

Pour obtenir une borne inférieure, intégrez la fonction constante 2 sur la région\(R\). Pour obtenir une borne supérieure, intégrez la fonction constante 13 sur la région\(R\).

\[\begin{align*} \int_1^2 \int_1^3 2 \,dx \, dy &= \int_1^2 [2x\bigg|_1^3] \,dy = \int_1^2 2(2)dy = 4y\bigg|_1^2 = 4(2 - 1) = 4 \\[4pt] \int_1^2 \int_1^3 13dx \, dy &= \int_1^2 [13x\bigg|_1^3] \,dy = \int_1^2 13(2)\,dy = 26y\bigg|_1^2 = 26(2 - 1) = 26. \end{align*}\]

Par conséquent, nous obtenons\(\displaystyle 4 \leq \iint_R (x^2 + y^2) \,dA \leq 26.\)

Exemple\(\PageIndex{5}\): Illustrating Property vi

Évaluez l'intégrale\(\displaystyle \iint_R e^y \cos x \, dA\) sur la région\(R = \big\{(x,y)\,| \, 0 \leq x \leq \frac{\pi}{2}, \, 0 \leq y \leq 1 \big\}\).

Solution

C'est un excellent exemple pour la propriété vi car la fonction\(f(x,y)\) est clairement le produit de deux fonctions à variable unique\(e^y\) et\(\cos x\). Ainsi, nous pouvons diviser l'intégrale en deux parties, puis intégrer chacune d'elles en tant que problème d'intégration à variable unique.

\ [\ begin {align*} \ iInt_R e^y \ cos x \, dA &= \ int_0^1 \ int_0^ {\ pi/2} e^y \ cos x \, dx \, dy \ \ [4pt]
&= \ left (\ int_0^1 e^y dy \ right) \ left (\ int_0^ {\ pi/2} \ cos x \, dx \ right) \ \ [4 points]
&= (e^y \ bigg|_0^1) (\ sin x \ bigg|_0^ {\ pi/2}) \ \ [4 points]
&= e - 1. \ end {align*} \]

Exercice\(\PageIndex{2}\)

a. Utiliser les propriétés de l'intégrale double et du théorème de Fubini pour évaluer l'intégrale

\[\int_0^1 \int_{-1}^3 (3 - x + 4y) \,dy \, dx. \nonumber \]

b. Montrez-le\(\displaystyle 0 \leq \iint_R \sin \pi x \, \cos \pi y \, dA \leq \frac{1}{32}\) où\(R = \left(0, \frac{1}{4}\right)\left(\frac{1}{4}, \frac{1}{2}\right)\).

Allusion

Utilisez les propriétés i. et ii. et évaluez l'intégrale itérée, puis utilisez la propriété v.

Réponse

un.\(26\)

b. Les réponses peuvent varier.

Comme nous l'avons mentionné précédemment, lorsque nous utilisons des coordonnées rectangulaires, la double intégrale sur une région\(R\) désignée par\(\iint_R f(x,y) \, dA\) peut être écrite comme\(\iint_R\, f(x,y) \, dx \, dy\) ou.\(\iint_R \, f(x,y) \,dy \, dx.\) L'exemple suivant montre que les résultats sont les mêmes quel que soit l'ordre d'intégration que nous choisissons.

Exemple\(\PageIndex{6}\): Evaluating an Iterated Integral in Two Ways

Revenons à la fonction\(f(x,y) = 3x^2 - y\) de l'exemple 1, cette fois sur la région rectangulaire\(R = [0,2] \times [0,3]\). Utilisez le théorème de Fubini pour évaluer de deux\(\iint_R f(x,y) \,dA\) manières différentes :

1. Intégrez d'abord par rapport à,\(y\) puis par rapport à\(x\) ;
2. Intégrez d'abord par rapport à,\(x\) puis par rapport à\(y\).

Solution

La figure\(\PageIndex{6}\) montre comment le calcul fonctionne de deux manières différentes.

1. Intégrez d'abord en ce qui concerne,\(y\) puis intégrez en ce qui concerne\(x\) :

\ [\ begin {align*} \ IInt_R f (x, y) \, dA &= \ int_ {x=0} ^ {x=2} \ int_ {y=0} ^ {y=3} (3x^2 - y) \, dy \, dx \ \ [4 points]
&= \ int_ {x=0} ^ {x=2} \ left (\ int_ {y=0} ^ {y=3} (3x^2 - y) \, dy \ right) \, dx = \ int_ {x=0} ^ {x=2} \ left [3x^2y - \ frac {y^2} {2} \ bigg|_ {y=0} ^ {y=3} \ droite] \, dx \ \ [4 points]
&= \ int_ {x=0} ^ {x=2} \ left (9x^2 - \ frac {9} {2} \ right) \, dx = 3x^3 - \ frac {9} {2} x \ bigg|_ {x=0} ^ {x=2} = 15. \ end {align*} \]

2. Intégrez d'abord par rapport à,\(x\) puis intégrez par rapport à\(y\) :
    \ [\ begin {align*} \ Iint_R f (x, y) \, dA &= \ int_ {y=0} ^ {y=3} \ int_ {x=0} ^ {x=2} (3x^2 - y) \, dx \, dy \ \ [4pt]
   &= \ int_ {y=0} ^ {y=3} \ left (\ int_ {x=0} ^ {x=2} (3x^2 - y) \, dx \ right) \, dy \ \ [4 points]
   &= \ int_ {y=0} ^ {y=3} \ left [x^3 - xy \ bigg|_ {x=0} ^ {x=2} \ right] dy \ \ [4 points]
   &= \ int_ {y=0} ^ {y=3} (8 - 2 ans) \, dy = 8 ans - y^2 \ bigg|_ {y=3} (8 - 2 ans) \, dy = 8 ans - y^2 \ bigg|_ {y =0} ^ {y=3} = 15. \ end {align*} \]

Analyse

Quel que soit l'ordre d'intégration, la double intégrale nous donne une réponse à\(15\). Nous pouvons interpréter cette réponse comme un volume en unités cubiques du solide situé en\(S\) dessous de la fonction\(f(x,y) = 3x^2 - y\) au-dessus de la région\(R = [0,2] \times [0,3]\). Cependant, n'oubliez pas que l'interprétation d'une intégrale double en tant que volume (non signé) ne fonctionne que lorsque l'integrand\(f\) est une fonction non négative sur la région de base\(R\).

Exercice\(\PageIndex{3}\)

Évaluer

\[\int_{y=-3}^{y=2} \int_{x=3}^{x=5} (2 - 3x^2 + y^2) \,dx \, dy. \nonumber \]

Allusion

Utilisez le théorème de Fubini.

Réponse

\(-\frac{1340}{3}\)

Dans l'exemple suivant, nous voyons qu'il peut être avantageux de changer l'ordre d'intégration pour faciliter le calcul. Nous reviendrons sur cette idée à plusieurs reprises dans ce chapitre.

Exemple\(\PageIndex{7}\): Switching the Order of Integration

Considérez la double intégrale\(\displaystyle \iint_R x \, \sin (xy) \, dA\) sur la région\(R = \big\{(x,y) \,| \, 0 \leq x \leq \pi, \, 1 \leq y \leq 2 \big\}\) (Figure\(\PageIndex{7}\)).

1. Exprimez la double intégrale de deux manières différentes.
2. Déterminez s'il est plus facile d'évaluer la double intégrale d'une manière que de l'autre et pourquoi.
3. Evaluez l'intégrale.

Figure\(\PageIndex{7}\) : La fonction\(z = f(x,y) = x \, \sin(xy)\) sur la région rectangulaire\(R = [0,\pi ] \times [1,2].\)

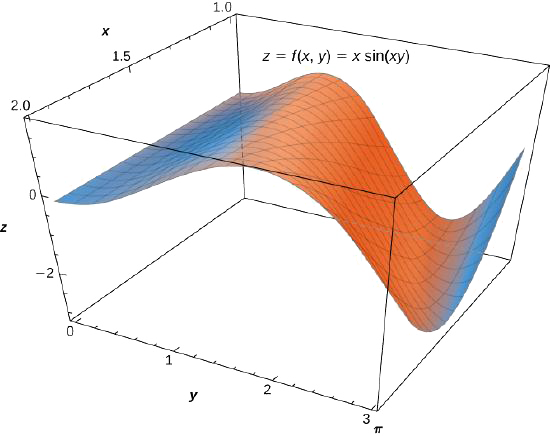
1. Nous pouvons nous exprimer\(\iint_R x \, \sin (xy) \,dA\) de deux manières : d'abord en intégrant par rapport à\(y\) et ensuite par rapport à\(x\) ; ensuite en intégrant par rapport à\(x\) et ensuite par rapport à\(y\).
   \[\iint_R x \, \sin (xy) \,dA= \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \,dy \, dx \nonumber \]
   Intégrez d'abord par rapport à\(y\).
   \[= \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \, \sin (xy) \,dx \, dy \nonumber \]
   Intégrez d'abord par rapport à\(x\).
2. Si nous voulons d'abord intégrer par rapport à y, puis intégrer par rapport à\(x\), nous voyons que nous pouvons utiliser la substitution\(u = xy\), qui donne\(du = x \, dy\). Par conséquent, l'intégrale intérieure est simple\(\int \sin u \, du\) et nous pouvons modifier les limites pour qu'elles soient fonction de\(x\),

\[\iint_R x \, \sin (xy) \,dA = \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \, dy \, dx = \int_{x=0}^{x=\pi} \left[\int_{u=x}^{u=2x} \sin (u) \,du \right] \, dx.\nonumber \]

Cependant, intégrer par rapport à d'\(x\)abord, puis intégrer par rapport à\(y\) nécessite une intégration par parties pour l'intégrale intérieure, avec\(u = x\) et\(dv = \sin(xy)dx\)

Alors\(du = dx\)\(v = - \frac{\cos(xy)}{y}\) et donc

\[\iint_R x \sin(xy) \,dA = \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \sin(xy) \,dx \, dy = \int_{y=1}^{y=2} \left[ - \frac{x \, \cos (xy)}{y} \bigg|_{x=0}^{x=\pi} + \frac{1}{y} \int_{x=0}^{x=\pi} \cos(xy)\,dx \right] \, dy.\nonumber \]

L'évaluation devenant de plus en plus complexe, nous n'effectuerons que le calcul le plus facile à faire, ce qui est clairement la première méthode.

3. Évaluez la double intégrale de la manière la plus simple.

\ [\ begin {align*} \ Iint_R x \, \ sin (xy) \, dA &= \ int_ {x=0} ^ {x= \ pi} \ int_ {y=1} ^ {y=2} x \, \ sin (xy) \, dy \, dx \ \ [4 points]
&= \ int_ {x=0} ^ {x= \ pi} \ left [\ int_ {u=x} ^ {u=2x} \ sin (u) \, du \ right] \, dx = \ int_ {x=0} ^ {x= \ pi} \ left [- \ cos u \ bigg|_ {u=x} ^ {u=2x} \ right] \, dx \ \ [4 points]
&= \ int _ {x=0} ^ {x= \ pi} (- \ cos 2x + \ cos x) \, dx \ \ [4 points]
&= \ left (- \ frac {1} {2} \ sin 2x + \ sin x \ right) \ bigg|_ {x=0} ^ {x= \ pi} = 0. \ end {align*} \]

Exercice\(\PageIndex{4}\)

Évaluez l'intégrale\(\displaystyle \iint_R xe^{xy}\,dA\) où\(R = [0,1] \times [0, \ln 5]\).

Allusion

Intégrez en respectant le\(y\) premier.

Réponse

\(\frac{4 - \ln 5}{\ln 5}\)

Applications des intégrales doubles

Les intégrales doubles sont très utiles pour déterminer l'aire d'une région délimitée par des courbes de fonctions. Nous décrivons cette situation plus en détail dans la section suivante. Toutefois, si la région est de forme rectangulaire, nous pouvons trouver son aire en intégrant la fonction constante\(f(x,y) = 1\) sur la région\(R\).

Définition : Superficie d'une région R

La superficie de la région\(R\) est donnée par\[A(R) = \iint_R 1 \, dA. \nonumber \]

Cette définition est logique car l'utilisation\(f(x,y) = 1\) et l'évaluation de l'intégrale en font un produit de longueur et de largeur. Examinons cette formule à l'aide d'un exemple et voyons comment elle fonctionne.

Exemple\(\PageIndex{8}\): Finding Area Using a Double Integral

Déterminez la superficie de la région en\(R = \big\{\,(x,y)\,|\,0 \leq x \leq 3, \, 0 \leq y \leq 2\big\}\) utilisant une double intégrale, c'est-à-dire en intégrant\(1\) la région\(R\).

Solution

La région est rectangulaire en longueur\(3\) et en largeur\(2\), nous savons donc que c'est le cas\(6\). Nous obtenons la même réponse lorsque nous utilisons une double intégrale :

\[A(R) = \int_0^2 \int_0^3 1 \, dx \, dy = \int_0^2 \left[x\big|_0^3\right] \, dy = \int_0^2 3 dy = 3 \int_0^2 dy = 3y\bigg|_0^2 = 3(2) = 6 \, \text{units}^2.\nonumber \]

Nous avons déjà vu comment les intégrales doubles peuvent être utilisées pour trouver le volume d'un solide délimité au-dessus par une fonction\(f(x,y) \geq 0\) sur une région\(R\) fournie\(f(x,y) \geq 0\) pour all\((x,y)\) in\(R\). Voici un autre exemple pour illustrer ce concept.

Exemple\(\PageIndex{9}\): Volume of an Elliptic Paraboloid

Déterminez le volume\(V\) du solide\(S\) délimité par le paraboloïde elliptique\(2x^2 + y^2 + z = 27\), les plans\(x = 3\) et et\(y = 3\) les trois plans de coordonnées.

Solution

Remarquez d'abord le graphique de la surface\(z = 27 - 2x^2 - y^2\) sur la Figure\(\PageIndex{8}\) (a) et au-dessus de la zone carrée\(R_1 = [-3,3] \times [-3,3]\). Cependant, nous avons besoin du volume du solide délimité par le paraboloïde elliptique\(2x^2 + y^2 + z = 27\), les plans\(x = 3\) et\(y = 3\), et les trois plans de coordonnées.

Figure\(\PageIndex{8}\) : (a) La surface\(z = 27 - 2x^2 - y^2\) au-dessus de la zone carrée\(R1 = [−3,3] \times [−3,3]\). (b) Le solide\(S\) se trouve sous la surface\(z = 27 - 2x^2 - y^2\) au-dessus de la zone carrée\(R1 = [0,3] \times [0,3]\).

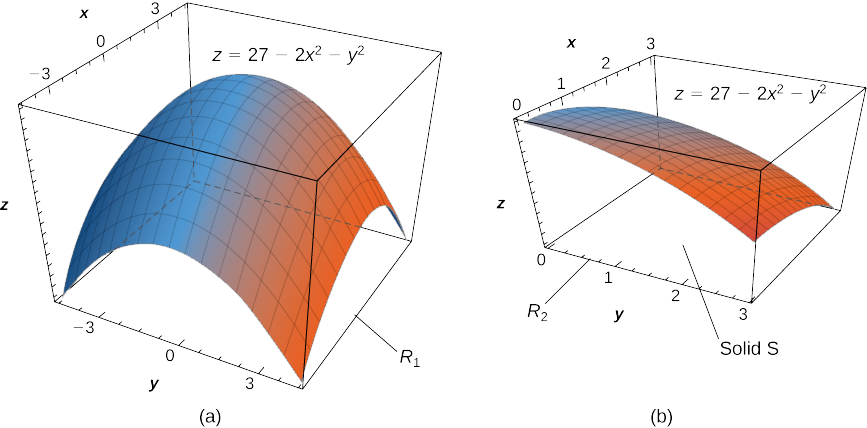
Regardons maintenant le graphique de la surface de la Figure\(\PageIndex{8}\) (b). Nous déterminons le volume\(V\) en évaluant la double intégrale sur\(R_2\) :

\ [\ begin {align*} V &= \ iInt_R z \, dA = \ iInt_R (27 - 2x^2 - y^2) \, dA \ \ [4 points]
&= \ int_ {y=0} ^ {y=3} \ int_ {x=0} ^ {x=3} (27 - 2x^2 - y^2) \, dx \, et dy & \ text {Convertir en intégrale littérale.} \ \ [4pt]
&= \ int_ {y=0} ^ {y=3} [27x - \ frac {2} {3} x^3 - y^2x] \ bigg|_ {x=0} ^ {x=3} \ , dy & & \ text {Intégrer par rapport à $x$.} \ \ [4pt]
&= \ int_ {y=0} ^ {y=3} (63 - 3y^2) dy = 63 y - y^3 \ bigg|_ {y=0} ^ {y=3} = 162. \ end {align*} \]

Exercice\(\PageIndex{5}\)

Détermine le volume du solide délimité au-dessus par le graphique du\(xy\) plan\(f(x,y) = xy \sin(x^2y)\) -et du dessous par le plan sur la région rectangulaire\(R = [0,1] \times [0,\pi]\).

Allusion

Tracez la fonction, configurez l'intégrale et utilisez une intégrale itérée.

Réponse

\(\frac{\pi}{2}\)

Rappelons que nous avons défini la valeur moyenne d'une fonction d'une variable sur un intervalle\([a,b]\) comme

\[f_{ave} = \frac{1}{b - a} \int_a^b f(x) \, dx. \nonumber \]

De même, nous pouvons définir la valeur moyenne d'une fonction de deux variables sur une région \(R\). La principale différence est que nous divisons par une surface plutôt que par la largeur d'un intervalle.

Définition : valeur moyenne d'une fonction

La valeur moyenne d'une fonction de deux variables sur une région\(R\) est

\[F_{ave} = \frac{1}{\text{Area of} \, R} \iint_R f(x,y)\, dx \, dy. \nonumber \]

Dans l'exemple suivant, nous trouvons la valeur moyenne d'une fonction sur une région rectangulaire. C'est un bon exemple d'obtention d'informations utiles pour une intégration en effectuant des mesures individuelles sur une grille, au lieu d'essayer de trouver une expression algébrique pour une fonction.

Exemple\(\PageIndex{10}\): Calculating Average Storm Rainfall

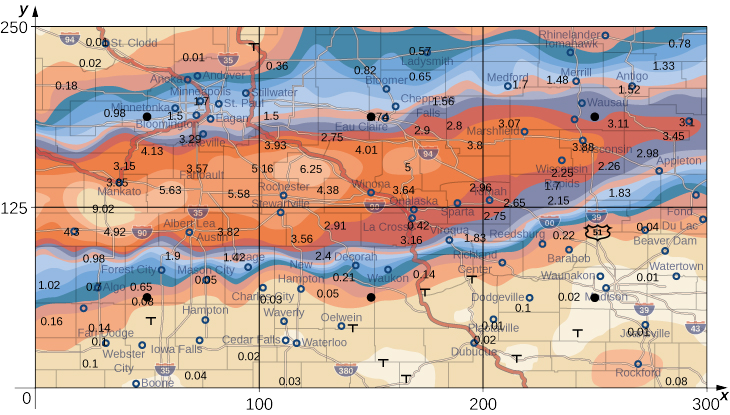
La carte météorologique de la figure\(\PageIndex{9}\) montre un système de tempête exceptionnellement humide associé aux vestiges de l'ouragan Karl, qui a déversé 4 à 8 pouces (100 à 200 mm) de pluie dans certaines parties du Midwest les 22 et 23 septembre 2010. La zone de précipitations mesurait 300 miles d'est en ouest et 250 miles du nord au sud. Estimez les précipitations moyennes sur l'ensemble de la région au cours de ces deux jours.

Figure\(\PageIndex{9}\) : Effets de l'ouragan Karl, qui a déversé 4 à 8 pouces (100 à 200 mm) de pluie dans certaines parties du sud-ouest du Wisconsin, du sud du Minnesota et du sud-est du Dakota du Sud sur une distance de 300 miles d'est en ouest et de 250 miles du nord au sud.

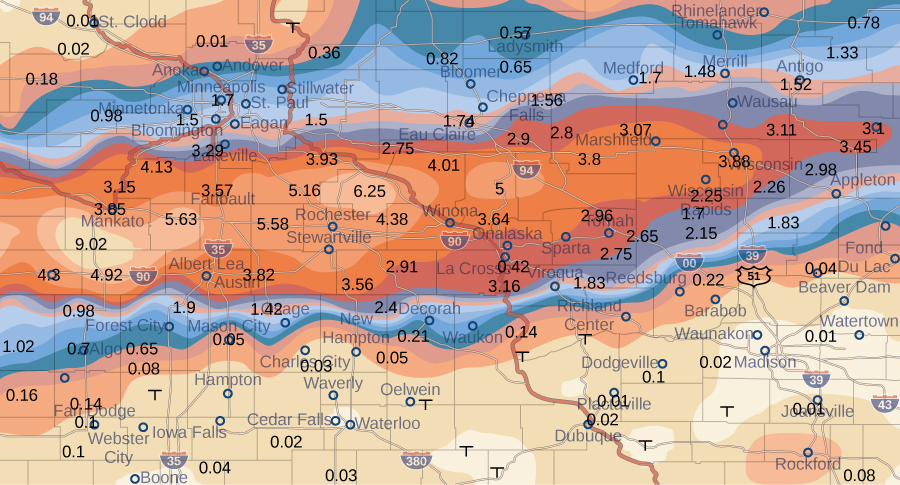
Solution

Placez l'origine dans le coin sud-ouest de la carte afin que toutes les valeurs puissent être considérées comme se trouvant dans le premier quadrant et qu'elles soient donc toutes positives. Divisez maintenant la carte entière en six rectangles\((m = 2\) et\(n = 3)\), comme indiqué sur la figure\(\PageIndex{9}\). \(f(x,y)\)Suppose indique les précipitations orageuses en pouces à un point situé à environ\(x\) miles à l'est de l'origine et à des\(y\) miles au nord de l'origine. \(R\)Représentez l'ensemble de la superficie en miles\(250 \times 300 = 75000\) carrés. Ensuite, la surface de chaque sous-rectangle est

\[\Delta A = \frac{1}{6} (75000) = 12500.\nonumber \]

Supposons que ce\((x_{ij}*,y_{ij}*)\) sont approximativement les points médians de chaque sous-rectangle\(R_{ij}\). Notez la région codée par couleur à chacun de ces points et estimez les précipitations. Les précipitations à chacun de ces points peuvent être estimées comme suit :

• À (\(x_{11}, y_{11}\)), les précipitations sont de 0.08.
• À (\(x_{12}, y_{12}\)), les précipitations sont de 0.08.
• À (\(x_{13}, y_{13}\)), les précipitations sont de 0,01
• À (\(x_{21}, y_{21}\)), la précipitation est de 1.70.
• À (\(x_{22}, y_{22}\)), la précipitation est de 1.74.
• À (\(x_{23}, y_{23}\)), la précipitation est de 3,00.

Figure\(\PageIndex{10}\) : Pluie de pluie avec des axes rectangulaires et montrant les points médians de chaque sous-rectangle.

Selon notre définition, les précipitations orageuses moyennes dans l'ensemble de la région au cours de ces deux jours étaient

\ [\ begin {align*} f_ {ave} = \ frac {1} {Zone \, R} \ Iint_R f (x, y) \, dx \, dy &= \ frac {1} {75000} \ iInt_R f (x, y) \, dx \, dy \ \ [4 points]
& \ approx \ frac {1} {75000} \ sumée _ {i=1} ^3 \ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*) \ Delta A \ \ [4 points]
&= \ frac {1} {75000} \ Bigg [f (x_ {11} ^*, y_ {11} ^*) \ Delta A + f (x_ {12} ^*, y_ {12} ^*) \ Delta A + f (x_ {13} ^*, y_ {13} ^*) \ Delta A + f (x_ {21} ^*, y_ {21} ^*) \ Delta A + f (x_ {22} ^*, y_ {22} ^*) \ Delta A + f (x_ {22} ^*) \ Delta A + f (x_ {22} ^*) \ Delta A + f (x_ {22} ^*) \ Delta A + f (x_ {22} ^*)} ^*, y_ {23} ^*) \ Delta A \ Bigg] \ \ [4 points]
& \ approx \ frac {1} {75 000} \ Big [0,08 + 0,08 + 0,01 + 0,01 + 1,70 + 1,74 + 3,00 \ Grand] \ Delta A \ \ [4 points]
&= \ frac {1} {75000} \ Big [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00 \ Grand] 12 500 \ \ [4 points]
&= \ frac {1} {6} \ Grand [0,08 + 0,08 + 0,08 + 0,01 + 1,70 + 1,70 + 1,74 + 3,00 \ Grand] \\[4pt] &\approx 1.10 \;\text{in}. \end{align*}\]

Du 22 au 23 septembre 2010, cette région a connu une pluviométrie moyenne d'environ 1,10 pouce.

Exercice\(\PageIndex{6}\)

Une carte de contour est affichée pour une fonction\(f(x,y)\) sur le rectangle\(R = [-3,6] \times [-1, 4]\).

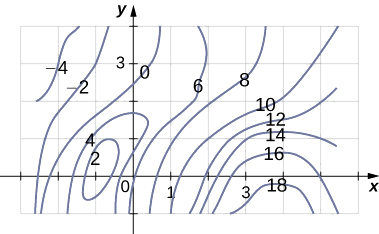
a. Utilisez la règle du point médian avec\(m = 3\) et\(n = 2\) pour estimer la valeur de\(\displaystyle \iint_R f(x,y) \,dA.\)

b. Estimez la valeur moyenne de la fonction\(f(x,y)\).

Allusion

Divisez la région en six rectangles et utilisez les lignes de contour pour estimer les valeurs de\(f(x,y)\).

Réponse

Les réponses aux deux parties a. et b. peuvent varier.

Concepts clés

• Nous pouvons utiliser une double somme de Riemann pour approximer le volume d'un solide délimité au-dessus par une fonction de deux variables sur une région rectangulaire. En prenant la limite, cela devient une double intégrale représentant le volume du solide.
• Les propriétés des intégrales doubles sont utiles pour simplifier le calcul et déterminer les limites de leurs valeurs.
• Nous pouvons utiliser le théorème de Fubini pour écrire et évaluer une intégrale double en tant qu'intégrale itérée.
• Les intégrales doubles sont utilisées pour calculer l'aire d'une région, le volume sous une surface et la valeur moyenne d'une fonction de deux variables sur une région rectangulaire.

Équations clés

• \[\iint_R f(x,y) \,dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(x_ij*,y_ij*)\,ΔA\nonumber \]
• \[\int_a^b \int_c^d f(x,y)\,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \,dy \right] dx\nonumber \]ou

  \[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d\left[ \int_a^b f(x,y) \,dx \right] dy\nonumber \]

• \[f_{ave} = \frac{1}{\text{Area of}\, R} \iint_R f(x,y) \,dx \, dy\nonumber \]

Lexique

double intégrale

de la fonction\(f(x,y)\) sur la\(R\) région du\(xy\) plan -est définie comme la limite d'une double somme de Riemann,

\[ \iint_R f(x,y) \,dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A.\nonumber \]

double somme de Riemann

de la fonction\(f(x,y)\) sur une région rectangulaire\(R\) est

\[\sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A,\nonumber \]

où\(R\) est divisé en sous-rectangles plus petits\(R_{ij}\) et\((x_{ij}^*, y_{ij}^*)\) est un point arbitraire dans\(R_{ij}\)

Théorème de Fubini

si\(f(x,y)\) est une fonction de deux variables qui est continue sur une région rectangulaire\(R = \big\{(x,y) \in \mathbb{R}^2 \,|\,a \leq x \leq b, \, c \leq y \leq d\big\}\), alors la double intégrale de\(f\) au-dessus de la région est égale à une intégrale itérée,

\[\displaystyle\iint_R f(x,y) \, dA = \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_c^d \int_a^b f(x,y) \,dx \, dy\nonumber \]

intégrale itérée

pour une fonction\(f(x,y)\) sur la région\(R\) est

un.\(\displaystyle \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \, dy\right] \, dx,\)

b.\(\displaystyle \int_c^d \int_a^b f(x,y) \, dx \, dy = \int_c^d \left[\int_a^b f(x,y) \, dx\right] \, dy,\)

où\(a,b,c\) et\(d\) sont des nombres réels et\(R = [a,b] \times [c,d]\)