Skip to main content
Global

15.1E : Exercices pour la section 15.1

  1. Last updated
  2. Save as PDF
  • Page ID
    197440

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 et 2, utilisez la règle du point médian avec\(m = 4\) et\(n = 2\) pour estimer le volume du solide délimité par la surface\(z = f(x,y)\), les plans verticaux\(x = 1\)\(x = 2\),\(y = 1\), et\(y = 2\), et le plan horizontal\(x = 0\).

    1)\(f(x,y) = 4x + 2y + 8xy\)

    Réponse
    \(27\)

    2)\(f(x,y) = 16x^2 + \frac{y}{2}\)

    Dans les exercices 3 et 4, estimez le volume du solide sous la surface\(z = f(x,y)\) et au-dessus de la région rectangulaire R en utilisant une somme de Riemann\(m = n = 2\) et les points d'échantillonnage comme étant les coins inférieurs gauches des sous-rectangles de la partition.

    3)\(f(x,y) = \sin x - \cos y\),\(R = [0, \pi] \times [0, \pi]\)

    Réponse
    \(0\)

    4)\(f(x,y) = \cos x + \cos y\),\(R = [0, \pi] \times [0, \frac{\pi}{2}]\)

    5) Utilisez la règle du point médian avec\(m = n = 2\) pour estimer\(\iint_R f(x,y) \,dA\), où les valeurs de la fonction f on\(R = [8,10] \times [9,11]\) sont données dans le tableau suivant.

    \(y\)
    \(x\) \ (y \) « >9 9.5 10 10,5 11
    8 \ (y \) « >9,8 5 6.7 5 5.6
    8.5 \ (y \) « >9,4 4,5 8 5.4 3.4
    9 \ (y \) « >8,7 4.6 6 5.5 3.4
    9.5 \ (y \) « >6,7 6 4,5 5.4 6.7
    10 \ (y \) « >6,8 6.4 5.5 5.7 6,8
    Réponse
    \(21.3\)

    6) Les valeurs de la fonction\(f\) sur le rectangle\(R = [0,2] \times [7,9]\) sont données dans le tableau suivant. Estimez l'intégrale double\(\iint_R f(x,y)\,dA\) en utilisant une somme de Riemann avec\(m = n = 2\). Sélectionnez les points d'échantillonnage qui constitueront les coins supérieurs droits des sous-carrés de R.

    \(y_0 = 7\) \(y_1 = 8\) \(y_2 = 9\)
    \(x_0 = 0\) \ (y_0 = 7 \) « >10,22 \ (y_1 = 8 \) « >10,21 \ (y_2 = 9 \) « >9,85
    \(x_1 = 1\) \ (y_0 = 7 \) « >6,73 \ (y_1 = 8 \) « >9,75 \ (y_2 = 9 \) « >9,63
    \(x_2 = 2\) \ (y_0 = 7 \) « >5,62 \ (y_1 = 8 \) « >7,83 \ (y_2 = 9 \) « >8,21

    7) La profondeur d'une piscine pour enfants de 4 pieds sur 4 pieds, mesurée à intervalles de 1 pied, est donnée dans le tableau suivant.

    1. Estimez le volume d'eau de la piscine en utilisant une somme de Riemann avec\(m = n = 2\). Sélectionnez les points d'échantillonnage en utilisant la règle du point médian sur\(R = [0,4] \times [0,4]\).
    2. Déterminez la profondeur moyenne de la piscine.
      \(y\)
      \(x\) \ (y \) « >0 1 2 3 4
      0 \ (y \) « >1 1,5 2 2,5 3
      1 \ (y \) « >1 1,5 2 2,5 3
      2 \ (y \) « >1 1,5 1,5 2,5 3
      3 \ (y \) « >1 1 1,5 2 2,5
      4 \ (y \) « >1 1 1 1,5 2
    Réponse
    a. 28\(\text{ft}^3\)
    b. 1,75 pieds

    8) La profondeur d'un trou de 3 pieds sur 3 pieds dans le sol, mesurée à des intervalles de 1 pied, est donnée dans le tableau suivant.

    1. Estimez le volume du trou en utilisant une somme de Riemann avec\(m = n = 3\) et en utilisant les points d'échantillonnage comme étant les coins supérieurs gauches des sous-carrés de \(R\).
    2. Détermine la profondeur moyenne du trou.
      \(y\)
      \(x\) \ (y \) « >0 1 2 3
      0 \ (y \) « >6 6,5 6.4 6
      1 \ (y \) « >6,5 7 7,5 6,5
      2 \ (y \) « >6,5 6.7 6,5 6
      3 \ (y \) « >6 6,5 5 5.6

    9) Les courbes\(f(x,y) = k\) de niveau de la fonction\(f\) sont données dans le graphique suivant, où\(k\) est une constante.

    1. Appliquez la règle du point médian avec\(m = n = 2\) pour estimer la double intégrale\(\iint_R f(x,y)\,dA\), où\(R = [0.2,1] \times [0,0.8]\).
    2. Estimez la valeur moyenne de la fonction\(f\) sur\(R\).

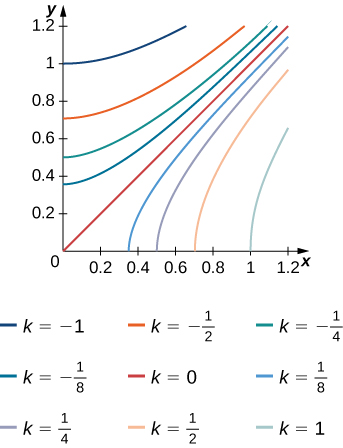
    Réponse
    a. 0,112
    b.\(f_{ave} ≃ 0.175\) ; ici\(f(0.4,0.2) ≃ 0.1\),\(f(0.2,0.6) ≃− 0.2\)\(f(0.8,0.2) ≃ 0.6\), et\(f(0.8,0.6) ≃ 0.2\)

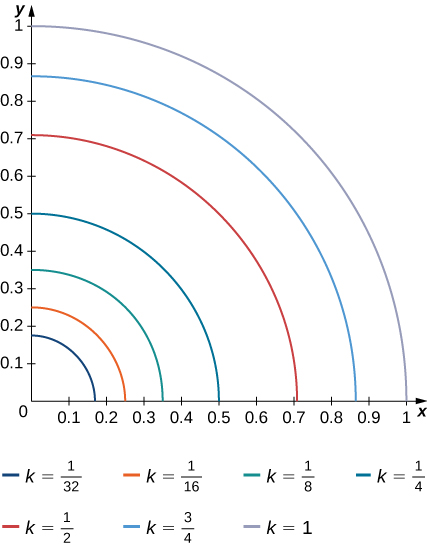
    10) Les courbes\(f(x,y) = k\) de niveau de la fonction\(f\) sont données dans le graphique suivant, où\(k\) est une constante.

    1. Appliquez la règle du point médian avec\(m = n = 2\) pour estimer la double intégrale\(\iint_R f(x,y)\,dA\), où\(R = [0.1,0.5] \times [0.1,0.5]\).
    2. Estimez la valeur moyenne de la fonction f on\(R\).

    11) Le solide situé sous la surface\(z = \sqrt{4 - y^2}\) et au-dessus de la région rectangulaire\( R = [0,2] \times [0,2]\) est illustré dans le graphique suivant. Évaluez la double intégrale\(\iint_Rf(x,y)\),\(f(x,y) = \sqrt{4 - y^2}\) en trouvant le volume du solide correspondant.

    Réponse
    \(2\pi\)

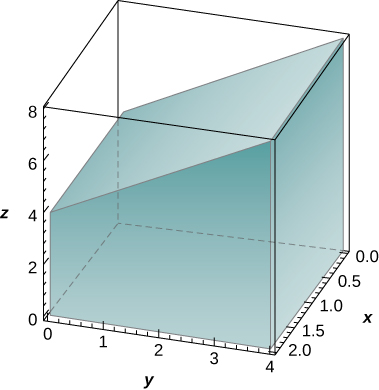
    12) Le solide situé sous le plan\(z = y + 4\) et au-dessus de la région rectangulaire\(R = [0,2] \times [0,4]\) est illustré dans le graphique suivant. Évaluez la double intégrale\(\iint_R f(x,y)\,dA\)\(f(x,y) = y + 4\), où, en trouvant le volume du solide correspondant.

    Dans les exercices 13 à 20, calculez les intégrales en inversant l'ordre d'intégration.

    13)\(\displaystyle \int_{-1}^1\left(\int_{-2}^2 (2x + 3y + 5)\,dx \right) \space dy\)

    Réponse
    \(40\)

    (14)\(\displaystyle \int_0^2\left(\int_0^1 (x + 2e^y + 3)\,dx \right) \space dy\)

    (15)\(\displaystyle \int_1^{27}\left(\int_1^2 (\sqrt[3]{x} + \sqrt[3]{y})\,dy \right) \space dx\)

    Réponse
    \(\frac{81}{2} + 39\sqrt[3]{2}\)

    16)\(\displaystyle \int_1^{16}\left(\int_1^8 (\sqrt[4]{x} + 2\sqrt[3]{y})\,dy \right) \space dx\)

    17)\(\displaystyle \int_{\ln 2}^{\ln 3}\left(\int_0^1 e^{x+y}\,dy \right) \space dx\)

    Réponse
    \(e - 1\)

    18)\(\displaystyle \int_0^2\left(\int_0^1 3^{x+y}\,dy \right) \space dx\)

    19)\(\displaystyle \int_1^6\left(\int_2^9 \frac{\sqrt{y}}{x^2}\,dy \right) \space dx\)

    Réponse
    \(15 - \frac{10\sqrt{2}}{9}\)

    (20)\(\displaystyle \int_1^9 \left(\int_4^2 \frac{\sqrt{x}}{y^2}\,dy \right)\,dx\)

    Dans les exercices 21 à 34, évaluez les intégrales itérées en choisissant l'ordre d'intégration.

    (21)\(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \sin(2x)\cos(3y)\,dx \space dy\)

    Réponse
    \(0\)

    (22)\(\displaystyle \int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)]\,dx \space dy\)

    23)\(\displaystyle \int_1^e \int_1^e \left[\frac{1}{x}\sin(\ln x) + \frac{1}{y}\cos (\ln y)\right] \,dx \space dy\)

    Réponse
    \((e − 1)(1 + \sin 1 − \cos 1)\)

    (24)\(\displaystyle \int_1^e \int_1^e \frac{\sin(\ln x)\cos (\ln y)}{xy} \,dx \space dy\)

    25)\(\displaystyle \int_1^2 \int_1^2 \left(\frac{\ln y}{x} + \frac{x}{2y + 1}\right)\,dy \space dx\)

    Réponse
    \(\frac{3}{4}\ln \left(\frac{5}{3}\right) + 2 (\ln 2)^2 - \ln 2\)

    (26)\(\displaystyle \int_1^e \int_1^2 x^2 \ln(x)\,dy \space dx\)

    (27)\(\displaystyle \int_1^{\sqrt{3}} \int_1^2 y \space \arctan \left(\frac{1}{x}\right) \,dy \space dx\)

    Réponse
    \(\frac{1}{8}[(2\sqrt{3} - 3) \pi + 6 \space \ln 2]\)

    (28)\(\displaystyle \int_0^1 \int_0^{1/2} (\arcsin x + \arcsin y)\,dy \space dx\)

    (29)\(\displaystyle \int_0^1 \int_1^2 xe^{x+4y}\,dy \space dx\)

    Réponse
    \(\frac{1}{4}e^4 (e^4 - 1)\)

    (30)\(\displaystyle \int_1^2 \int_0^1 xe^{x-y}\,dy \space dx\)

    31)\(\displaystyle \int_1^e \int_1^e \left(\frac{\ln y}{\sqrt{y}} + \frac{\ln x}{\sqrt{x}}\right)\,dy \space dx\)

    Réponse
    \(4(e - 1)(2 - \sqrt{e})\)

    32)\(\displaystyle \int_1^e \int_1^e \left(\frac{x \space \ln y}{\sqrt{y}} + \frac{y \space \ln x}{\sqrt{x}}\right)\,dy \space dx\)

    33)\(\displaystyle \int_0^1 \int_1^2 \left(\frac{x}{x^2 + y^2} \right)\,dy \space dx\)

    Réponse
    \(-\frac{\pi}{4} + \ln \left(\frac{5}{4}\right) - \frac{1}{2} \ln 2 + \arctan 2\)

    34)\(\displaystyle \int_0^1 \int_1^2 \frac{y}{x + y^2}\,dy \space dx\)

    Dans les exercices 35 à 38, trouvez la valeur moyenne de la fonction sur les rectangles donnés.

    35)\(f(x,y) = −x +2y\),\(R = [0,1] \times [0,1]\)

    Réponse
    \(\frac{1}{2}\)

    36)\(f(x,y) = x^4 + 2y^3\),\(R = [1,2] \times [2,3]\)

    37)\(f(x,y) = \sinh x + \sinh y\),\(R = [0,1] \times [0,2]\)

    Réponse
    \(\frac{1}{2}(2 \space \cosh 1 + \cosh 2 - 3)\).

    38)\(f(x,y) = \arctan(xy)\),\(R = [0,1] \times [0,1]\)

    39)\(g\) Soyons\(f\) deux fonctions continues telles que\(0 \leq m_1 \leq f(x) \leq M_1\) pour tous\(x ∈ [a,b]\) et\(0 \leq m_2 \leq g(y) \leq M_2\) pour tous\( y ∈ [c,d]\). Montrez que l'inégalité suivante est vraie :

    \[m_1m_2(b-a)(c-d) \leq \int_a^b \int_c^d f(x) g(y)\,dy dx \leq M_1M_2 (b-a)(c-d). \nonumber \]

    Dans les exercices 40 à 43, utilisez la propriété v. des intégrales doubles et la réponse de l'exercice précédent pour montrer que les inégalités suivantes sont vraies.

    40)\(\frac{1}{e^2} \leq \iint_R e^{-x^2 - y^2} \space dA \leq 1\), où\(R = [0,1] \times [0,1]\)

    41)\(\frac{\pi^2}{144} \leq \iint_R \sin x \cos y \space dA \leq \frac{\pi^2}{48}\), où\(R = \left[ \frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[ \frac{\pi}{6}, \frac{\pi}{3}\right]\)

    42)\(0 \leq \iint_R e^{-y}\space \cos x \space dA \leq \frac{\pi}{2}\), où\(R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]\)

    43)\(0 \leq \iint_R (\ln x)(\ln y) \,dA \leq (e - 1)^2\), où\(R = [1, e] \times [1, e] \)

    44)\(g\) Soyons\(f\) deux fonctions continues telles que\(0 \leq m_1 \leq f(x) \leq M_1\) pour tous\(x ∈ [a,b]\) et\(0 \leq m_2 \leq g(y) \leq M_2\) pour tous\(y ∈ [c,d]\). Montrez que l'inégalité suivante est vraie :

    \[(m_1 + m_2) (b - a)(c - d) \leq \int_a^b \int_c^d |f(x) + g(y)| \space dy \space dx \leq (M_1 + M_2)(b - a)(c - d) \nonumber \]

    Dans les exercices 45 à 48, utilisez la propriété v. des intégrales doubles et la réponse de l'exercice précédent pour montrer que les inégalités suivantes sont vraies.

    45)\(\frac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) \,dA \leq 2\), où\(R = [0,1] \times [0,1]\)

    46)\(\frac{\pi^2}{36}\iint_R (\sin x + \cos y)\,dA \leq \frac{\pi^2 \sqrt{3}}{36}\), où\(R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]\)

    47)\(\frac{\pi}{2}e^{-\pi/2} \leq \iint_R (\cos x + e^{-y})\,dA \leq \pi\), où\(R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]\)

    48)\(\frac{1}{e} \leq \iint_R (e^{-y} - \ln x) \,dA \leq 2\), où\(R = [0, 1] \times [0, 1]\)

    Dans les exercices 49 à 50, la fonction\(f\) est donnée en termes d'intégrales doubles.

    1. Déterminez la forme explicite de la fonction\(f\).
    2. Déterminez le volume du solide sous la surface\(z = f(x,y)\) et au-dessus de la région\(R\).
    3. Trouvez la valeur moyenne de la fonction\(f\) sur\(R\).
    4. Utilisez un système d'algèbre informatique (CAS) pour tracer\(z = f(x,y)\) et\(z = f_{ave}\) dans le même système de coordonnées.

    49) [T]\(f(x,y) = \int_0^y \int_0^x (xs + yt) ds \space dt\), où\((x,y) \in R = [0,1] \times [0,1]\)

    Réponse

    a.\(f(x,y) = \frac{1}{2} xy (x^2 + y^2)\) ;
    b.\(V = \int_0^1 \int_0^1 f(x,y)\,dx \space dy = \frac{1}{8}\) ;
    c.\(f_{ave} = \frac{1}{8}\) ;

    d.

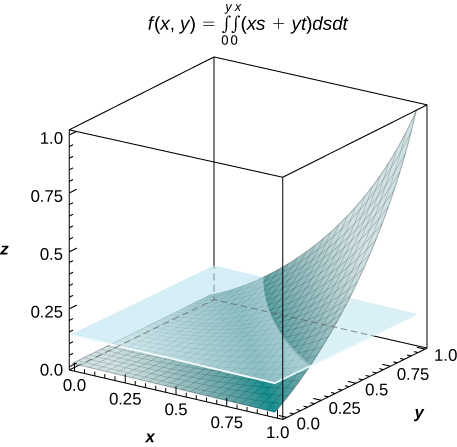
    50) [T]\(f(x,y) = \int_0^x \int_0^y [\cos(s) + \cos(t)] \, dt \space ds\), où\((x,y) \in R = [0,3] \times [0,3]\)

    51) Montrez que si\(f\) et\(g\) sont continus\([a,b]\) et\([c,d]\), respectivement, alors

    \(\displaystyle \int_a^b \int_c^d |f(x) + g(y)| dy \space dx = (d - c) \int_a^b f(x)\,dx\)

    \(\displaystyle + \int_a^b \int_c^d g(y)\,dy \space dx = (b - a) \int_c^d g(y)\,dy + \int_c^d \int_a^b f(x)\,dx \space dy\).

    52) Montrez cela\(\displaystyle \int_a^b \int_c^d yf(x) + xg(y)\,dy \space dx = \frac{1}{2} (d^2 - c^2) \left(\int_a^b f(x)\,dx\right) + \frac{1}{2} (b^2 - a^2) \left(\int_c^d g(y)\,dy\right)\).

    53) [T] Considérez la fonction\(f(x,y) = e^{-x^2-y^2}\), où\((x,y) \in R = [−1,1] \times [−1,1]\).

    1. Utilisez la règle du point médian avec\(m = n = 2,4,..., 10\) pour estimer l'intégrale double\(I = \iint_R e^{-x^2 - y^2} dA\). Arrondissez vos réponses au centième le plus proche.
    2. Pour\(m = n = 2\), trouvez la valeur moyenne de f sur la région R. Arrondissez votre réponse au centième le plus proche.
    3. Utilisez un CAS pour représenter graphiquement, dans le même système de coordonnées, le solide dont le volume est donné par\(\iint_R e^{-x^2-y^2} dA\) et le plan\(z = f_{ave}\).
    Réponse

    a. Pour\(m = n = 2\),\(I = 4e^{-0.5} \approx 2.43\)
    b.\(f_{ave} = e^{-0.5} \simeq 0.61\) ;

    c.

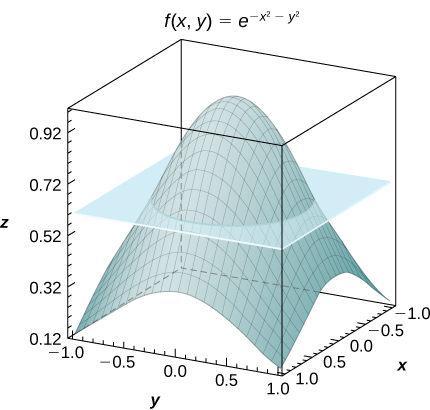
    54) [T] Considérez la fonction\(f(x,y) = \sin (x^2) \space \cos (y^2)\), où\((x,y \in R = [−1,1] \times [−1,1]\).

    1. Utilisez la règle du point médian avec\(m = n = 2,4,..., 10\) pour estimer l'intégrale double\(I = \iint_R \sin (x^2) \cos (y^2) \space dA\). Arrondissez vos réponses au centième le plus proche.
    2. Pour\(m = n = 2\), trouvez la valeur moyenne de l'ensemble de\(f\) la région R. Arrondissez votre réponse au centième le plus proche.
    3. Utilisez un CAS pour représenter graphiquement, dans le même système de coordonnées, le solide dont le volume est donné par\(\iint_R \sin(x^2) \cos(y^2) \space dA\) et le plan\(z = f_{ave}\).

    Dans les exercices 55 à 56, les fonctions\(f_n\) sont données, où\(n \geq 1\) est un entier naturel.

    1. Déterminez le volume des solides\(S_n\) sous les surfaces\(z = f_n(x,y)\) et au-dessus de la région\(R\).
    2. Déterminez la limite des volumes des solides à\(S_n\) mesure qu'\(n\)ils augmentent sans limite.

    55)\(f(x,y) = x^n + y^n + xy, \space (x,y) \in R = [0,1] \times [0,1]\)

    Réponse
    a.\(\frac{2}{n + 1} + \frac{1}{4}\)
    b.\(\frac{1}{4}\)

    56)\(f(x,y) = \frac{1}{x^n} + \frac{1}{y^n}, \space (x,y) \in R = [1,2] \times [1,2]\)

    57) Montrez que la valeur moyenne d'une fonction\(f\) sur une région rectangulaire\(R = [a,b] \times [c,d]\) est\(f_{ave} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\), où se\((x_{ij}^*,y_{ij}^*)\) trouvent les points d'échantillonnage de la partition de\(R\), où\(1 \leq i \leq m\) et\(1 \leq j \leq n\).

    58) Utilisez la règle du point médian avec\(m = n\) pour montrer que la valeur moyenne d'une fonction\(f\) sur une région rectangulaire\(R = [a,b] \times [c,d]\) est approximée par

    \[f_{ave} \approx \frac{1}{n^2} \sum_{i,j =1}^n f \left(\frac{1}{2} (x_{i=1} + x_i), \space \frac{1}{2} (y_{j=1} + y_j)\right). \nonumber \]

    59) Une carte isotherme est une carte reliant des points ayant la même température à un moment donné pendant une période donnée. Utilisez l'exercice précédent et appliquez la règle du point médian avec\(m = n = 2\) pour trouver la température moyenne dans la région indiquée dans la figure suivante.

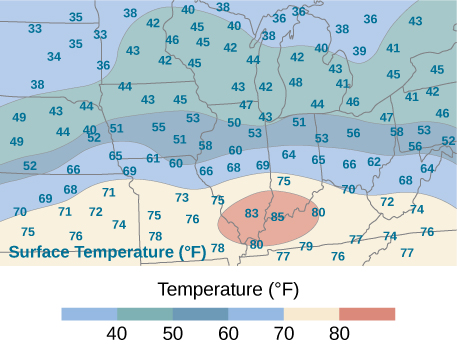
    Réponse
    \(56.5^{\circ}\)F ; ici\(f(x_1^*,y_1^*) = 71, \space f(x_2^*, y_1^*) = 72, \space f(x_2^*,y_1^*) = 40, \space f(x_2^*,y_2^*) = 43\), où\(x_i^*\) et\(y_j^*\) sont les points médians des sous-intervalles des partitions de\([a,b]\) et\([c,d]\), respectivement.