11.5 : Sections coniques
- Page ID
- 197276
- Identifiez l'équation d'une parabole sous forme standard avec un focus et une directrice donnés.
- Identifiez l'équation d'une ellipse sous forme standard avec des foyers donnés.
- Identifiez l'équation d'une hyperbole sous forme standard avec des foyers donnés.
- Reconnaissez une parabole, une ellipse ou une hyperbole à partir de sa valeur d'excentricité.
- Écrivez l'équation polaire d'une section conique avec excentricité\(e\).
- Déterminez quand une équation générale de degré deux est une parabole, une ellipse ou une hyperbole.
Les sections coniques sont étudiées depuis l'époque des Grecs anciens et étaient considérées comme un concept mathématique important. Dès 320 av. J.-C., des mathématiciens grecs tels que Ménaechme, Appollonius et Archimède étaient fascinés par ces courbes. Appollonius a écrit un traité complet en huit volumes sur les sections coniques dans lequel il a pu, par exemple, dériver une méthode spécifique pour identifier une section conique grâce à l'utilisation de la géométrie. Depuis lors, d'importantes applications des sections coniques sont apparues (par exemple, en astronomie), et les propriétés des sections coniques sont utilisées dans les radiotélescopes, les récepteurs d'antennes paraboliques et même dans l'architecture. Dans cette section, nous discutons des trois sections coniques de base, de certaines de leurs propriétés et de leurs équations.
Les sections coniques tirent leur nom du fait qu'elles peuvent être générées en croisant un plan avec un cône. Un cône comporte deux parties de forme identique appelées nappes. Une nappe est ce que la plupart des gens entendent par « cône », ayant la forme d'un chapeau de fête. Un cône circulaire droit peut être généré en faisant tourner une ligne passant par l'origine autour de l'axe y, comme indiqué sur la figure\(\PageIndex{1}\).
Les sections coniques sont générées par l'intersection d'un plan avec un cône (Figure\(\PageIndex{2}\)). Si le plan est parallèle à l'axe de révolution (axe y), alors la section conique est une hyperbole. Si le plan est parallèle à la ligne génératrice, la section conique est une parabole. Si le plan est perpendiculaire à l'axe de révolution, la section conique est un cercle. Si le plan coupe une nappe selon un angle par rapport à l'axe (autre que
Paraboles
Une parabole est générée lorsqu'un plan croise un cône parallèle à la ligne de génération. Dans ce cas, l'avion ne croise qu'une seule des nappes. Une parabole peut également être définie en termes de distances.
Une parabole est l'ensemble de tous les points dont la distance par rapport à un point fixe, appelé foyer, est égale à la distance par rapport à une ligne fixe, appelée directrice. Le point situé à mi-chemin entre le foyer et la directrice est appelé sommet de la parabole.
Un graphique d'une parabole typique apparaît sur la figure\(\PageIndex{3}\). En utilisant ce diagramme en conjonction avec la formule de distance, nous pouvons dériver une équation pour une parabole. Rappelez-vous la formule de distance : étant donné le point P avec des coordonnées\((x_1,y_1)\) et le point Q avec des coordonnées,\((x_2,y_2),\) la distance qui les sépare est donnée par la formule
\[d(P,Q)=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Ensuite, à partir de la définition d'une parabole et de la figure\(\PageIndex{3}\), nous obtenons
\[d(F,P)=d(P,Q) \nonumber \]
\[\sqrt{(0−x)^2+(p−y)^2}=\sqrt{(x−x)^2+(−p−y)^2}. \nonumber \]
Mise au carré des deux côtés et simplification des rendements
\[ \begin{align} x^2+(p−y)^2 = 0^2+(−p−y)^2 \\ x^2+p^2−2py+y^2 = p^2+2py+y^2 \\ x^2−2py =2py \\ x^2 =4py. \end{align} \nonumber \]
Supposons maintenant que nous souhaitions déplacer le sommet. Nous utilisons les variables\((h,k)\) pour indiquer les coordonnées du sommet. Ensuite, si le focus se trouve directement au-dessus du sommet, il possède\((h,k+p)\) des coordonnées et la directrice possède l'équation\(y=k−p\). En utilisant la même dérivation, on obtient la formule\((x−h)^2=4p(y−k)\). La résolution de cette équation pour\(y\) conduit au théorème suivant.
Étant donné une parabole s'ouvrant vers le haut avec un sommet situé à\((h,k)\) et un foyer situé à\((h,k+p)\), où\(p\) est une constante, l'équation de la parabole est donnée par
\[y=\dfrac{1}{4p}(x−h)^2+k. \nonumber \]
Il s'agit de la forme standard d'une parabole.
Nous pouvons également étudier les cas où la parabole s'ouvre vers le bas, vers la gauche ou vers la droite. L'équation pour chacun de ces cas peut également être écrite sous forme standard, comme indiqué dans les graphiques suivants.
De plus, l'équation d'une parabole peut être écrite sous une forme générale, bien que sous cette forme les valeurs de\(h\)\(k\), et ne\(p\) soient pas immédiatement reconnaissables. La forme générale d'une parabole s'écrit
\[ax^2+bx+cy+d=0 \label{para1} \]
ou
\[ay^2+bx+cy+d=0.\label{para2} \]
L'équation \ ref {para1} représente une parabole qui s'ouvre vers le haut ou vers le bas. L'équation \ ref {para2} représente une parabole qui s'ouvre soit vers la gauche soit vers la droite. Pour mettre l'équation sous forme standard, utilisez la méthode qui consiste à compléter le carré.
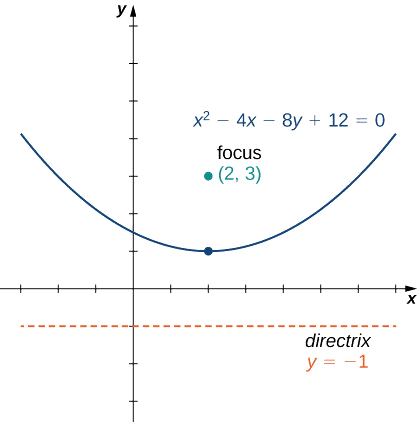
Mettez l'équation
\[x^2−4x−8y+12=0 \nonumber \]
sous forme standard et représente graphiquement la parabole résultante.
Solution
Comme y n'est pas au carré dans cette équation, nous savons que la parabole s'ouvre soit vers le haut soit vers le bas. Nous devons donc résoudre cette équation pour y, ce qui mettra l'équation sous forme standard. Pour ce faire, ajoutez\(8y\) d'abord les deux côtés de l'équation :
\[8y=x^2−4x+12. \nonumber \]
L'étape suivante consiste à compléter le carré sur le côté droit. Commencez par regrouper les deux premiers termes sur le côté droit à l'aide de parenthèses :
\[8y=(x^2−4x)+12. \nonumber \]
Déterminez ensuite la constante qui, lorsqu'elle est ajoutée entre parenthèses, fait de la quantité entre parenthèses un trinôme carré parfait. Pour ce faire, prenez la moitié du coefficient de x et mettez-le au carré. Cela donne\((\dfrac{−4}{2})^2=4.\) Add 4 entre parenthèses et soustrait 4 en dehors des parenthèses, de sorte que la valeur de l'équation ne soit pas modifiée :
\[8y=(x^2−4x+4)+12−4. \nonumber \]
Combinez maintenant des termes similaires et factorisez la quantité entre parenthèses :
\[8y=(x−2)^2+8. \nonumber \]
Enfin, divisez par 8 :
\[y=\dfrac{1}{8}(x−2)^2+1. \nonumber \]
Cette équation est maintenant sous forme standard. La comparaison avec l'équation donne\(h=2, k=1\), et\(p=2\). La parabole s'ouvre, avec le sommet\((2,1)\), le focus et la directrice\(y=−1\).\((2,3)\) Le graphique de cette parabole apparaît comme suit.
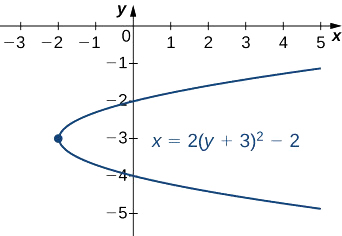
Mettez l'\(2y^2−x+12y+16=0\)équation sous forme standard et tracez la parabole résultante.
- Allusion
-
Résolvez pour\(x\). Vérifiez dans quelle direction s'ouvre la parabole.
- Réponse
-
\[x=2(y+3)^2−2 \nonumber \]
L'axe de symétrie d'une parabole verticale (s'ouvrant vers le haut ou vers le bas) est une ligne verticale passant par le sommet. La parabole possède une propriété réfléchissante intéressante. Supposons que nous ayons une antenne parabolique à section parabolique. Si un faisceau d'ondes électromagnétiques, telles que de la lumière ou des ondes radio, entre dans l'antenne en ligne droite à partir d'un satellite (parallèlement à l'axe de symétrie), les ondes sont réfléchies sur l'antenne et se collectent au centre de la parabole, comme indiqué.
Prenons l'exemple d'une antenne parabolique conçue pour recueillir les signaux d'un satellite dans l'espace. L'antenne est dirigée directement vers le satellite et un récepteur est situé au centre de la parabole. Les ondes radio provenant du satellite sont réfléchies par la surface de la parabole vers le récepteur, qui collecte et décode les signaux numériques. Cela permet à un petit récepteur de recueillir des signaux provenant d'un grand angle de ciel. Les lampes de poche et les phares d'une voiture fonctionnent selon le même principe, mais en sens inverse : la source de lumière (c'est-à-dire l'ampoule) est située au foyer et la surface réfléchissante du miroir parabolique focalise le faisceau droit devant. Cela permet à une petite ampoule d'éclairer un grand angle d'espace devant la lampe de poche ou la voiture.
Ellipses
Une ellipse peut également être définie en termes de distances. Dans le cas d'une ellipse, il y a deux foyers (pluriel de focus) et deux directrices (pluriel de directrix). Nous examinerons les directives plus en détail plus loin dans cette section.
Une ellipse est l'ensemble de tous les points pour lesquels la somme de leurs distances par rapport à deux points fixes (les foyers) est constante.
Un graphique d'une ellipse typique est illustré sur la figure\(\PageIndex{6}\). Dans cette figure, les foyers sont étiquetés comme\(F\) et\(F′\). Les deux sont à la même distance fixe par rapport à l'origine, et cette distance est représentée par la variable\(c\). Par conséquent, les coordonnées de\(F\) sont\((c,0)\) et les coordonnées de\(F′\) sont\((−c,0).\) Les points\(P\) et\(P′\) sont situés aux extrémités du grand axe de l'ellipse, et ont des coordonnées\((a,0)\) et\((−a,0)\), respectivement. L'axe principal correspond toujours à la distance la plus longue à travers l'ellipse et peut être horizontal ou vertical. Ainsi, la longueur du grand axe de cette ellipse est de\(2a\). De plus,\(P\) et\(P′\) sont appelés sommets de l'ellipse. Les points A\(Q\) et\(Q′\) sont situés aux extrémités du petit axe de l'ellipse et ont des coordonnées\((0,b)\) et\((0,−b),\) respectivement. L'axe secondaire est la distance la plus courte à travers l'ellipse. L'axe secondaire est perpendiculaire à l'axe principal.
Selon la définition de l'ellipse, nous pouvons choisir n'importe quel point de l'ellipse et la somme des distances entre ce point et les deux foyers est constante. Supposons que nous choisissions le point\(P\). Puisque les coordonnées du point\(P\) sont\((a,0),\) la somme des distances est
\[d(P,F)+d(P,F′)=(a−c)+(a+c)=2a. \nonumber \]
Par conséquent, la somme des distances à partir d'un point arbitraire A avec des coordonnées\((x,y)\) est également égale à\(2a\). En utilisant la formule de distance, nous obtenons
\[d(A,F)+d(A,F′)=2a. \nonumber \]
\[\sqrt{(x−c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \nonumber \]
Soustrayez le deuxième radical des deux côtés et mettez les deux côtés au carré :
\[\sqrt{(x−c)^2+y^2}=2a−\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Maintenant, isolez le radical sur le côté droit et retrouvez le carré :
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx \nonumber \]
\[4a\sqrt{(x+c)^2+y^2}=4a^2+4cx \nonumber \]
\[\sqrt{(x+c)^2+y^2}=a+\dfrac{cx}{a} \nonumber \]
\[(x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}. \nonumber \]
Isolez les variables du côté gauche de l'équation et les constantes du côté droit :
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Divisez les deux côtés par\(a^2−c^2\). Cela donne l'équation
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Si nous nous référons à la figure\(\PageIndex{6}\), la longueur de chacun des deux segments de ligne verte est égale à\(a\). Cela est vrai parce que la somme des distances entre le point\(Q\)\(F\) et les foyers\(F′\) est égale à\(2a\), et les longueurs de ces deux segments de ligne sont égales. Ce segment de droite forme un triangle droit avec la longueur de l'hypoténuse\(a\) et la longueur des jambes\(b\) et\(c\). Du théorème de Pythagore,\(b^2+c^2=a^2\) et\(b^2=a^2−c^2\). Par conséquent, l'équation de l'ellipse devient
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \nonumber \]
Enfin, si le centre de l'ellipse est déplacé de l'origine vers un point\((h,k)\), nous avons la forme standard suivante d'une ellipse.
Considérez l'ellipse avec son centre\((h,k)\), un grand axe horizontal avec une longueur\(2a\) et un petit axe vertical avec une longueur\(2b\). Ensuite, l'équation de cette ellipse sous forme standard est
\[\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1 \label{HorEllipse} \]
et les foyers sont situés à\((h±c,k)\), où\(c^2=a^2−b^2\). Les équations des directrices sont\(x=h±\dfrac{a^2}{c}\).
Si l'axe principal est vertical, l'équation de l'ellipse devient
\[\dfrac{(x−h)^2}{b^2}+\dfrac{(y−k)^2}{a^2}=1 \label{VertEllipse} \]
et les foyers sont situés à\((h,k±c)\), où\(c^2=a^2−b^2\). Les équations des directrices dans ce cas sont\(y=k±\dfrac{a^2}{c}\).
Si l'axe principal est horizontal, l'ellipse est dite horizontale, et si l'axe principal est vertical, alors l'ellipse est dite verticale. L'équation d'une ellipse est sous forme générale si elle se trouve dans la forme
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
où A et B sont tous deux positifs ou négatifs. Pour convertir l'équation de la forme générale à la forme standard, utilisez la méthode qui consiste à compléter le carré.
Mettez l'équation
\[9x^2+4y^2−36x+24y+36=0 \nonumber \]
sous forme standard et tracez graphiquement l'ellipse résultante.
Solution
Soustrayez d'abord 36 des deux côtés de l'équation :
\[9x^2+4y^2−36x+24y=−36. \nonumber \]
Regroupez ensuite les\(x\) termes ensemble et les\(y\) termes ensemble, et éliminez le facteur commun :
\[(9x^2−36x)+(4y^2+24y)=−36 \nonumber \]
\[9(x^2−4x)+4(y^2+6y)=−36. \nonumber \]
Nous devons déterminer la constante qui, lorsqu'elle est ajoutée à l'intérieur de chaque ensemble de parenthèses, donne un carré parfait. Dans la première série de parenthèses, prenez la moitié du coefficient de x et mettez-le au carré. Cela donne\((\dfrac{−4}{2})^2=4.\) dans la deuxième série de parenthèses, prenez la moitié du coefficient de y et mettez-le au carré. Cela permet de les\((\dfrac{6}{2})^2=9.\) ajouter à l'intérieur de chaque paire de parenthèses. Comme le premier ensemble de parenthèses comporte un 9 à l'avant, nous en ajoutons 36 sur le côté gauche. De même, nous en ajoutons 36 au deuxième set. Par conséquent, l'équation devient
\[9(x^2−4x+4)+4(y^2+6y+9)=−36+36+36 \nonumber \]
\[9(x^2−4x+4)+4(y^2+6y+9)=36. \nonumber \]
Maintenant, factorisez les deux ensembles de parenthèses et divisez par 36 :
\[9(x−2)^2+4(y+3)^2=36 \nonumber \]
\[\dfrac{9(x−2)^2}{36}+\dfrac{4(y+3)^2}{36}=1 \nonumber \]
\[\dfrac{(x−2)^2}{4}+\dfrac{(y+3)^2}{9}=1. \nonumber \]
L'équation est maintenant sous forme standard. La comparaison avec l'équation \ ref {Vertellipse} donne\(h=2, k=−3, a=3,\) et\(b=2\). Il s'agit d'une ellipse verticale dont le centre est\((2,−3)\), l'axe principal 6 et l'axe secondaire 4. Le graphique de cette ellipse apparaît comme suit.

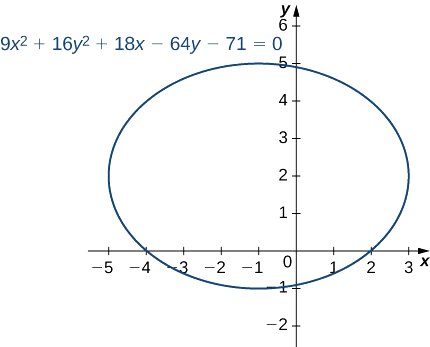
Mettez l'équation
\[9x^2+16y^2+18x−64y−71=0 \nonumber \]
sous forme standard et tracez graphiquement l'ellipse résultante.
- Allusion
-
Déplacez la constante et complétez le carré.
- Réponse
-
\[\dfrac{(x+1)^2}{16}+\dfrac{(y−2)^2}{9}=1 \nonumber \]
Selon la première loi du mouvement planétaire de Kepler, l'orbite d'une planète autour du Soleil est une ellipse avec le Soleil à l'un des foyers, comme le montre la Figure\(\PageIndex{8A}\). Comme l'orbite de la Terre est une ellipse, la distance par rapport au Soleil varie tout au long de l'année. Une idée fausse répandue est que la Terre est plus proche du Soleil en été. En effet, en été pour l'hémisphère nord, la Terre est plus éloignée du Soleil qu'en hiver. La différence de saison est due à l'inclinaison de l'axe de la Terre dans le plan orbital. Les comètes qui gravitent autour du Soleil, comme la comète de Halley, ont également des orbites elliptiques, tout comme les lunes orbitant autour des planètes et les satellites orbitant autour de la Terre.
Les ellipses possèdent également des propriétés réfléchissantes intéressantes : un rayon lumineux émanant d'un foyer passe par l'autre foyer après réflexion miroir dans l'ellipse. La même chose se produit également avec une onde sonore. Le National Statuary Hall du Capitole américain à Washington, DC, est une salle célèbre de forme elliptique, comme le montre la figure\(\PageIndex{8B}\). Cette salle a servi de lieu de réunion à la Chambre des représentants des États-Unis pendant près de cinquante ans. L'emplacement des deux foyers de cette pièce semi-elliptique est clairement identifié par des marques sur le sol, et même si la salle est pleine de visiteurs, lorsque deux personnes se tiennent debout à ces endroits et se parlent, elles peuvent s'entendre beaucoup plus clairement qu'elles ne peuvent entendre quelqu'un qui se trouve à proximité. La légende veut que John Quincy Adams ait placé son bureau sur l'un des foyers et qu'il ait pu espionner tous les autres membres de la Chambre sans avoir à se lever. Bien que cela constitue une bonne histoire, il est peu probable que ce soit vrai, car le plafond d'origine produisait tellement d'échos que toute la pièce a dû être suspendue avec des tapis pour atténuer le bruit. Le plafond a été reconstruit en 1902 et ce n'est qu'alors que le désormais célèbre effet de chuchotement est apparu. Une autre célèbre galerie de chuchotements, site de nombreuses demandes en mariage, se trouve à Grand Central Station à New York.
Hyperboles
Une hyperbole peut également être définie en termes de distances. Dans le cas d'une hyperbole, il existe deux foyers et deux directives. Les hyperboles présentent également deux asymptotes.
Une hyperbole est l'ensemble de tous les points où la différence entre leurs distances par rapport à deux points fixes (les foyers) est constante.
Le graphique d'une hyperbole typique apparaît comme suit.
La dérivation de l'équation d'une hyperbole sous forme standard est pratiquement identique à celle d'une ellipse. Un petit hic réside dans la définition : la différence entre deux nombres est toujours positive. \(P\)Soit un point sur l'hyperbole avec des coordonnées\((x,y)\). Ensuite, la définition de l'hyperbole donne\(|d(P,F_1)−d(P,F_2)|=constant\). Pour simplifier la dérivation, supposons que cela\(P\) se trouve sur la branche droite de l'hyperbole, de sorte que les barres de valeurs absolues tombent. S'il se trouve sur la branche gauche, la soustraction est inversée. Le sommet de la branche droite a des coordonnées\((a,0),\) donc
\[d(P,F_1)−d(P,F_2)=(c+a)−(c−a)=2a. \nonumber \]
Cette équation est donc vraie pour tout point de l'hyperbole. Revenir aux coordonnées\((x,y)\) pour\(P\) :
\[d(P,F_1)−d(P,F_2)=2a \nonumber \]
\[\sqrt{(x+c)^2+y^2}−\sqrt{(x−c)^2+y^2}=2a. \nonumber \]
Isolez le deuxième radical et mettez les deux côtés au carré :
\[\sqrt{(x−c)^2+y^2}=-2a+\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Maintenant, isolez le radical sur le côté droit et retrouvez le carré :
\(−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\)
\(-4a\sqrt{(x+c)^2+y^2}=−4a^2−4cx\)
\(-\sqrt{(x+c)^2+y^2}=−a−\dfrac{cx}{a}\)
\((x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}\).
Isolez les variables du côté gauche de l'équation et les constantes du côté droit :
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Enfin, divisez les deux côtés par\(a^2−c^2\). Cela donne l'équation
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Nous définissons maintenant b de telle sorte que\(b^2=c^2−a^2\). Cela est possible parce que\(c>a\). Par conséquent, l'équation de l'hyperbole devient
\[\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1. \nonumber \]
Enfin, si le centre de l'hyperbole est déplacé de l'origine au point,\((h,k),\) nous avons la forme standard suivante d'une hyperbole.
Considérez l'hyperbole avec un centre\((h,k)\), un grand axe horizontal et un petit axe vertical. Alors, l'équation de cette hyperbole est
\[\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1 \label{HorHyperbola} \]
et les foyers sont situés à l'\((h±c,k),\)endroit où\(c^2=a^2+b^2\). Les équations des asymptotes sont données par\(y=k±\dfrac{b}{a}(x−h).\) Les équations des directrices sont
\[x=h±\dfrac{a^2}{\sqrt{a^2+b^2}}=h±\dfrac{a^2}{c} \nonumber \]
Si l'axe principal est vertical, alors l'équation de l'hyperbole devient
\[\dfrac{(y−k)^2}{a^2}−\dfrac{(x−h)^2}{b^2}=1 \nonumber \]
et les foyers sont situés à l'\((h,k±c),\)endroit où\(c^2=a^2+b^2\). Les équations des asymptotes sont données par\(y=k±\dfrac{a}{b}(x−h)\). Les équations des directrices sont
\[y=k±\dfrac{a^2}{\sqrt{a^2+b^2}}=k±\dfrac{a^2}{c}. \nonumber \]
Si l'axe principal (axe transversal) est horizontal, alors l'hyperbole est dite horizontale, et si l'axe principal est vertical, alors l'hyperbole est dite verticale. L'équation d'une hyperbole est sous forme générale si elle est dans la forme
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
où A et B ont des signes opposés. Pour convertir l'équation de la forme générale à la forme standard, utilisez la méthode qui consiste à compléter le carré.
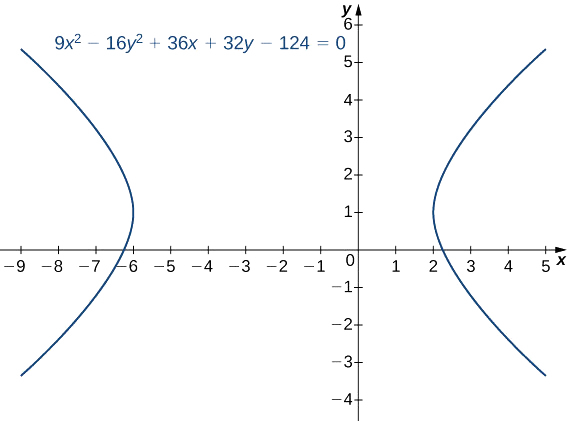
Mettez l'équation sous forme standard et\(9x^2−16y^2+36x+32y−124=0\) représentez graphiquement l'hyperbole qui en résulte. Quelles sont les équations des asymptotes ?
Solution
Ajoutez d'abord 124 des deux côtés de l'équation :
\(9x^2−16y^2+36x+32y=124.\)
Regroupez ensuite les termes x et les termes y, puis éliminez les facteurs communs :
\((9x^2+36x)−(16y^2−32y)=124\)
\(9(x^2+4x)−16(y^2−2y)=124\).
Nous devons déterminer la constante qui, lorsqu'elle est ajoutée à l'intérieur de chaque ensemble de parenthèses, donne un carré parfait. Dans la première série de parenthèses, prenez la moitié du coefficient de x et mettez-le au carré. Cela donne\((\dfrac{4}{2})^2=4\). Dans la deuxième série de parenthèses, prenez la moitié du coefficient de y et mettez-le au carré. Cela permet de les\((\dfrac{−2}{2})^2=1.\) ajouter à l'intérieur de chaque paire de parenthèses. Comme le premier ensemble de parenthèses comporte un 9 à l'avant, nous en ajoutons 36 sur le côté gauche. De même, nous soustrayons 16 du deuxième ensemble de parenthèses. Par conséquent, l'équation devient
\(9(x^2+4x+4)−16(y^2−2y+1)=124+36−16\)
\(9(x^2+4x+4)−16(y^2−2y+1)=144.\)
Ensuite, factorisez les deux ensembles de parenthèses et divisez-les par 144 :
\(9(x+2)^2−16(y−1)^2=144\)
\(\dfrac{9(x+2)^2}{144}−\dfrac{16(y−1)^2}{144}=1\)
\(\dfrac{(x+2)^2}{16}−\dfrac{(y−1)^2}{9}=1.\)
L'équation est maintenant sous forme standard. La comparaison avec l'équation \ ref {HorHyperbola} donne\(h=−2, k=1, a=4,\) et\(b=3\). Il s'agit d'une hyperbole horizontale avec un centre\((−2,1)\) et des asymptotes donnés par les équations\(y=1±\dfrac{3}{4}(x+2)\). Le graphique de cette hyperbole apparaît sur la figure\(\PageIndex{10}\).
Mettez l'équation sous forme standard et\(4y^2−9x^2+16y+18x−29=0\) représentez graphiquement l'hyperbole qui en résulte. Quelles sont les équations des asymptotes ?
- Allusion
-
Déplacez la constante et complétez le carré. Vérifiez dans quelle direction s'ouvre l'hyperbole
- Réponse
-
\(\dfrac{(y+2)^2}{9}−\dfrac{(x−1)^2}{4}=1.\)Il s'agit d'une hyperbole verticale. Asymptomtotes\(y=−2±\dfrac{3}{2}(x−1).\)

Les hyperboles possèdent également des propriétés réfléchissantes intéressantes. Un rayon dirigé vers un foyer d'une hyperbole est réfléchi par un miroir hyperbolique vers l'autre foyer. Ce concept est illustré dans la figure\(\PageIndex{11}\).
Cette propriété de l'hyperbole a des applications importantes. Il est utilisé pour la radiogoniométrie (puisque la différence entre les signaux provenant de deux tours est constante le long des hyperboles) et pour la construction de miroirs à l'intérieur des télescopes (pour réfléchir la lumière provenant du miroir parabolique vers l'oculaire). Un autre fait intéressant concernant les hyperboles est que, pour une comète qui entre dans le système solaire, si la vitesse est suffisante pour échapper à l'attraction gravitationnelle du Soleil, alors la trajectoire que la comète emprunte lorsqu'elle traverse le système solaire est hyperbolique.
Excentricité et Directrix
Une autre façon de décrire une section conique implique les directives, les foyers et une nouvelle propriété appelée excentricité. Nous verrons que la valeur de l'excentricité d'une section conique peut définir de manière unique cette conique.
L'excentricité \(e\)d'une section conique est définie comme étant la distance entre n'importe quel point de la section conique et son foyer, divisée par la distance perpendiculaire entre ce point et la directrice la plus proche. Cette valeur est constante pour n'importe quelle section conique et peut également définir la section conique :
- Si\(e=1\), la conique est une parabole.
- Si\(e<1\), c'est une ellipse.
- S'\(e>1,\)il s'agit d'une hyperbole.
L'excentricité d'un cercle est nulle. La directrice d'une section conique est la ligne qui, associée au point connu sous le nom de point focal, sert à définir une section conique. Les hyperboles et les ellipses non circulaires ont deux foyers et deux directives associées. Les paraboles ont un seul objectif et une seule directrice.
Les trois sections coniques avec leurs directives apparaissent sur la figure\(\PageIndex{12}\).
Souvenez-vous de la définition d'une parabole que la distance entre n'importe quel point de la parabole et le foyer est égale à la distance entre ce même point et la directrice. Par conséquent, par définition, l'excentricité d'une parabole doit être égale à 1. Les équations des directrices d'une ellipse horizontale sont\(x=±\dfrac{a^2}{c}\). Le sommet droit de l'ellipse est situé à\((a,0)\) et le point focal droit l'est\((c,0)\). Par conséquent, la distance entre le sommet et le foyer est\(a−c\) et la distance entre le sommet et la directrice droite est.\(\dfrac{a^2}{c}−c.\) Cela donne l'excentricité comme
\[e=\dfrac{a−c}{\dfrac{a^2}{c}−a}=\dfrac{c(a−c)}{a^2−ac}=\dfrac{c(a−c)}{a(a−c)}=\dfrac{c}{a}. \nonumber \]
En\(c<a\) effet, cette étape prouve que l'excentricité d'une ellipse est inférieure à 1. Les directives d'une hyperbole horizontale sont également situées à\(x=±\dfrac{a^2}{c}\), et un calcul similaire montre que l'excentricité d'une hyperbole l'est également\(e=\dfrac{c}{a}\). Cependant, dans ce cas, nous l'avons fait\(c>a\), donc l'excentricité d'une hyperbole est supérieure à 1.
Déterminer l'excentricité de l'ellipse décrite par l'équation
\(\dfrac{(x−3)^2}{16}+\dfrac{(y+2)^2}{25}=1.\)
Solution
D'après l'équation, nous voyons que\(a=5\) et\(b=4\). La valeur de c peut être calculée à l'aide de l'équation\(a^2=b^2+c^2\) d'une ellipse. En substituant les valeurs de a et b et en résolvant pour c, on obtient\(c=3\). Par conséquent, l'excentricité de l'ellipse est\(e=\dfrac{c}{a}=\dfrac{3}{5}=0.6.\)
Déterminer l'excentricité de l'hyperbole décrite par l'équation
\(\dfrac{(y−3)^2}{49}−\dfrac{(x+2)^2}{25}=1.\)
- Allusion
-
Trouvez d'abord les valeurs de a et b, puis déterminez c à l'aide de l'équation\(c^2=a^2+b^2\).
- Réponse
-
\(e=\dfrac{c}{a}=\dfrac{\sqrt{74}}{7}≈1.229\)
Équations polaires des sections coniques
Il est parfois utile d'écrire ou d'identifier l'équation d'une section conique sous forme polaire. Pour ce faire, nous avons besoin du concept du paramètre focal. Le paramètre focal d'une section conique p est défini comme la distance entre un foyer et la directrice la plus proche. Le tableau suivant donne les paramètres focaux pour les différents types de coniques, où a est la longueur du demi-grand axe (c'est-à-dire la moitié de la longueur du grand axe), c est la distance entre l'origine et le foyer et e est l'excentricité. Dans le cas d'une parabole, a représente la distance entre le sommet et le foyer.
| Conique | \(e\) | \(p\) |
|---|---|---|
| Ellipse | \ (e \) » style="vertical-align:middle ; « >\(0<e<1\) | \ (p \) » style="vertical-align:middle ; « >\(\dfrac{a^2−c^2}{c}=\dfrac{a(1−e^2)}{c}\) |
| Parabole | \ (e \) » style="vertical-align:middle ; « >\(e=1\) | \ (p \) » style="vertical-align:middle ; « >\(2a\) |
| Hyperbole | \ (e \) » style="vertical-align:middle ; « >\(e>1\) | \ (p \) » style="vertical-align:middle ; « >\(\dfrac{c^2−a^2}{c}=\dfrac{a(e^2−1)}{c}\) |
En utilisant les définitions du paramètre focal et de l'excentricité de la section conique, nous pouvons dériver une équation pour n'importe quelle section conique en coordonnées polaires. En particulier, nous supposons que l'un des foyers d'une section conique donnée se trouve au pôle. Ensuite, en utilisant la définition des différentes sections coniques en termes de distances, il est possible de prouver le théorème suivant.
L'équation polaire d'une section conique avec le paramètre focal p est donnée par
\(r=\dfrac{ep}{1±e\cos θ}\)ou\(r=\dfrac{ep}{1±e\sin θ}.\)
Dans l'équation de gauche, l'axe principal de la section conique est horizontal, et dans l'équation de droite, l'axe principal est vertical. Pour travailler avec une section conique écrite sous forme polaire, commencez par faire en sorte que le terme constant du dénominateur soit égal à 1. Cela peut être fait en divisant à la fois le numérateur et le dénominateur de la fraction par la constante qui apparaît devant le plus ou le moins du dénominateur. Ensuite, le coefficient du sinus ou du cosinus dans le dénominateur est l'excentricité. Cette valeur identifie la conique. Si le cosinus apparaît dans le dénominateur, la conique est horizontale. Si un sinus apparaît, la conique est verticale. Si les deux apparaissent, les axes pivotent. Le centre de la conique n'est pas nécessairement à l'origine. Le centre se trouve à l'origine uniquement si la conique est un cercle (c'est-à-dire\(e=0\)).
Identifier et créer un graphique de la section conique décrite par l'équation
\(r=\dfrac{3}{1+2\cos θ}\).
Solution
Le terme constant du dénominateur est 1, donc l'excentricité de la conique est 2. Il s'agit d'une hyperbole. Le paramètre focal p peut être calculé en utilisant l'équation\(ep=3.\) Since\(e=2\), cela donne\(p=\dfrac{3}{2}\). La fonction cosinus apparaît dans le dénominateur, de sorte que l'hyperbole est horizontale. Choisissez quelques valeurs pour\(θ\) et créez un tableau de valeurs. Ensuite, nous pouvons représenter graphiquement l'hyperbole (Figure\(\PageIndex{13}\)).
| \(θ\) | \(r\) | \(θ\) | \(r\) |
|---|---|---|---|
| \ (θ \) » style="vertical-align:middle ; « >0 | \ (r \) » style="vertical-align:middle ; « >1 | \ (θ \) » style="vertical-align:middle ; « >\(π\) | \ (r \) » style="vertical-align:middle ; « >−3 |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{4}\) | \ (r \) » style="vertical-align:middle ; « >\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{5π}{4}\) | \ (r \) » style="vertical-align:middle ; « >\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{2}\) | \ (r \) » style="vertical-align:middle ; « >3 | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{3π}{2}\) | \ (r \) » style="vertical-align:middle ; « >3 |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{3π}{4}\) | \ (r \) » style="vertical-align:middle ; « >\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{7π}{4}\) | \ (r \) » style="vertical-align:middle ; « >\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) |
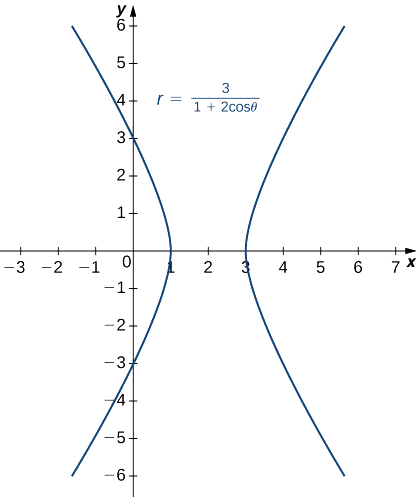
Identifier et créer un graphique de la section conique décrite par l'équation
\(r=\dfrac{4}{1−0.8 \sin θ}\).
- Allusion
-
Trouvez d'abord les valeurs de e et de p, puis créez un tableau de valeurs.
- Réponse
-
Ici\(e=0.8\) et\(p=5\). Cette section conique est une ellipse.
Équations générales du degré deux
Une équation générale de degré deux peut être écrite sous la forme
\[ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \nonumber \]
Le graphique d'une équation de cette forme est une section conique. \(B≠0\)Si tel est le cas, les axes de coordonnées sont pivotés. Pour identifier la section conique, nous utilisons le discriminant de la section conique\(4AC−B^2.\)
L'un des cas suivants doit être vrai :
- \(4AC−B^2>0\). Si tel est le cas, le graphique est une ellipse.
- \(4AC−B^2=0\). Si tel est le cas, le graphique est une parabole.
- \(4AC−B^2<0\). Si tel est le cas, le graphique est une hyperbole.
L'exemple le plus simple d'une équation du second degré impliquant un terme croisé est\(xy=1\). Cette équation peut être résolue\(y\) pour obtenir\(y=\dfrac{1}{x}\). Le graphe de cette fonction est appelé hyperbole rectangulaire, comme indiqué.
Les asymptotes de cette hyperbole sont les axes de\(y\) coordonnées\(x\) et. Pour déterminer l'angle θ de rotation de la section conique, nous utilisons la formule\(\cot 2θ=\frac{A−C}{B}\). Dans ce cas\(A=C=0\)\(\cot 2θ=(0−0)/1=0\) et\(B=1\) ainsi de suite\(θ=45°\). La méthode de représentation graphique d'une section conique avec des axes pivotés consiste à déterminer les coefficients de la conique dans le système de coordonnées pivoté. Les nouveaux coefficients sont étiquetés\(A′,B′,C′,D′,E′,\)\(F′,\) et sont donnés par les formules
\[ \begin{align} A′ =A\cos^ 2θ+B\cos θ\sin θ+C\sin^2 θ \\ B′ =0 \\ C′ =A\sin^2 θ−B\sin θ\cos θ+C\cos^2θ \\ D′ =D\cos θ+E\sin θ \\ E′ =−D\sin θ+E\cosθ \\ F′ =F. \end{align} \nonumber \]
La procédure pour représenter graphiquement une conique pivotée est la suivante :
- Identifiez la section conique à l'aide du discriminant\(4AC−B^2\).
- Déterminez\(θ\) en utilisant la formule\[\cot2θ=\dfrac{A−C}{B} \label{rot}. \]
- Calculez\(A′,B′,C′,D′,E′\), et\(F′\).
- Réécrivez l'équation d'origine en utilisant\(A′,B′,C′,D′,E′\), et\(F′\).
- Dessinez un graphique à l'aide de l'équation pivotée.
Identifiez la conique et calculez l'angle de rotation des axes pour la courbe décrite par l'équation
\[13x^2−6\sqrt{3}xy+7y^2−256=0. \nonumber \]
Solution
Dans cette équation,\(A=13,B=−6\sqrt{3},C=7,D=0,E=0,\) et\(F=−256\). Le discriminant de cette équation est
\[4AC−B^2=4(13)(7)−(−6\sqrt{3})^2=364−108=256. \nonumber \]
Cette conique est donc une ellipse.
Pour calculer l'angle de rotation des axes, utilisez l'équation \ ref {rot}
\[\cot 2θ=\dfrac{A−C}{B}. \nonumber \]
Cela donne
\(\cot 2θ=\dfrac{A−C}{B}=\dfrac{13−7}{−6\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\).
Donc\(2θ=120^o\) et\(θ=60^o\), quel est l'angle de rotation des axes.
Pour déterminer les coefficients pivotés, utilisez les formules ci-dessus :
\(A′=A\cos^2θ+B\cos θ\sinθ+C\sin^2θ\)
\(=13\cos^260+(−6\sqrt{3})\cos 60 \sin 60+7\sin^260\)
\(=13(\dfrac{1}{2})^2−6\sqrt{3}(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})+7(\dfrac{\sqrt{3}}{2})^2\)
\(=4,\)
\(B′=0\)
\(C′=A\sin^2θ−B\sin θ\cos θ+C\cos^2θ\)
\(=13\sin^260+(6\sqrt{3})\sin 60 \cos 60+7\cos^260\)
\(=13(\dfrac{\sqrt{3}}{2})^2+6\sqrt{3}(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})+7(\dfrac{1}{2})^2\)
\(=16,\)
\(D′=D\cos θ+E\sin θ\)
\(=(0)\cos 60+(0)\sin 60\)
\(=0,\)
\(E′=−D\sin θ+E\cos θ\)
\(=−(0)\sin 60+(0)\cos 60\)
\(=0\)
\(F′= F\)
\(=−256.\)
L'équation de la conique dans le système de coordonnées pivoté devient
\(4(x′)^2+16(y′)^2=256\)
\(\dfrac{(x′)^2}{64}+\dfrac{(y′)^2}{16}=1\).
Un graphique de cette section conique apparaît comme suit.
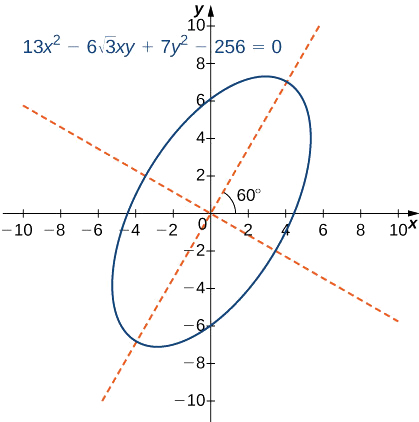
Identifiez la conique et calculez l'angle de rotation des axes pour la courbe décrite par l'équation
\[3x^2+5xy−2y^2−125=0. \nonumber \]
- Allusion
-
Suivez les étapes 1 et 2 de la méthode en cinq étapes décrite ci-dessus
- Réponse
-
La conique est une hyperbole et l'angle de rotation des axes est\(θ=22.5°.\)
Concepts clés
- L'équation d'une parabole verticale de forme standard avec un foyer et une directrice donnés\(p\) est la distance entre le sommet et le foyer et\((h,k)\) les coordonnées du sommet.\(y=\dfrac{1}{4p}(x−h)^2+k\)
- L'équation d'une ellipse horizontale sous forme standard est\(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) celle où le centre a des coordonnées\((h,k)\), l'axe principal a une longueur 2a, le petit axe a une longueur 2b et les coordonnées des foyers sont\((h±c,k)\), où\(c^2=a^2−b^2\).
- L'équation d'une hyperbole horizontale sous forme standard est celle\(\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1\) où le centre a des coordonnées\((h,k)\)\((h±a,k)\), les sommets sont situés et les coordonnées des foyers sont\((h±c,k),\) où\(c^2=a^2+b^2\).
- L'excentricité d'une ellipse est inférieure à 1, l'excentricité d'une parabole est égale à 1 et l'excentricité d'une hyperbole est supérieure à 1. L'excentricité d'un cercle est de 0.
- L'équation polaire d'une section conique avec excentricité e est\(r=\dfrac{ep}{1±ecosθ}\) ou\(r=\dfrac{ep}{1±esinθ}\), où p représente le paramètre focal.
- Pour identifier une conique générée par l'équation\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), calculez d'abord le discriminant\(D=4AC−B^2\). Si\(D>0\) alors la conique est une ellipse, si\(D=0\) alors la conique est une parabole, et si\(D<0\) alors la conique est une hyperbole.
Lexique
- section conique
- une section conique est toute courbe formée par l'intersection d'un plan avec un cône de deux nappes
- directrice
- une directrice (pluriel : directrices) est une ligne utilisée pour construire et définir une section conique ; une parabole a une directrice ; les ellipses et les hyperboles en ont deux
- discriminant
- la valeur\(4AC−B^2\), qui est utilisée pour identifier une conique lorsque l'équation contient un terme impliquant\(xy\), est appelée discriminant
- se concentrer
- un foyer (pluriel : foyers) est un point utilisé pour construire et définir une section conique ; une parabole a un foyer ; une ellipse et une hyperbole en ont deux
- excentricité
- l'excentricité est définie comme la distance entre un point quelconque de la section conique et son foyer divisée par la distance perpendiculaire entre ce point et la directrice la plus proche
- paramètre focal
- le paramètre focal est la distance entre le foyer d'une section conique et la directrice la plus proche
- formulaire général
- une équation d'une section conique écrite sous la forme d'une équation générale du second degré
- axe principal
- le grand axe d'une section conique passe par le sommet dans le cas d'une parabole ou par les deux sommets dans le cas d'une ellipse ou d'une hyperbole ; c'est également un axe de symétrie de la conique ; également appelé axe transversal
- axe mineur
- le petit axe est perpendiculaire au grand axe et coupe le grand axe au centre de la conique, ou au sommet dans le cas de la parabole ; également appelé axe conjugué
- nappe
- une nappe est la moitié d'un double cône
- formulaire standard
- une équation d'une section conique indiquant ses propriétés, telles que l'emplacement du sommet ou la longueur des axes principaux et secondaires
- sommet
- un sommet est un point extrême d'une section conique ; une parabole a un sommet à son point de rotation. Une ellipse possède deux sommets, un à chaque extrémité de l'axe principal ; une hyperbole possède deux sommets, l'un au point de rotation de chaque branche


