11.3 : Coordonnées polaires
- Page ID
- 197286
- Localisez des points dans un plan à l'aide de coordonnées polaires.
- Convertissez des points entre des coordonnées rectangulaires et des coordonnées polaires.
- Dessinez des courbes polaires à partir d'équations données
- Convertissez des équations entre des coordonnées rectangulaires et polaires.
- Identifier la symétrie dans les courbes et les équations polaires.
Le système de coordonnées rectangulaires (ou plan cartésien) permet de mapper des points en paires ordonnées et des paires ordonnées en points. C'est ce que l'on appelle une cartographie biunivoque entre des points du plan et des paires ordonnées. Le système de coordonnées polaires fournit une méthode alternative pour cartographier des points en paires ordonnées. Dans cette section, nous voyons que, dans certaines circonstances, les coordonnées polaires peuvent être plus utiles que les coordonnées rectangulaires.
Définition des coordonnées polaires
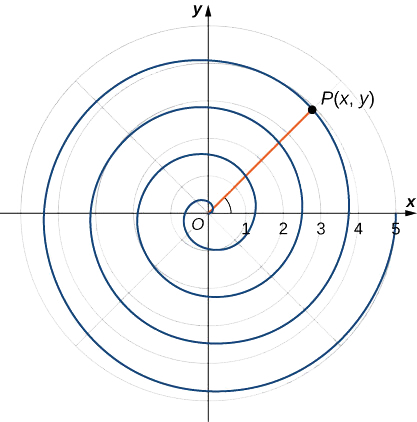
Pour trouver les coordonnées d'un point dans le système de coordonnées polaires, reportez-vous à la Figure\(\PageIndex{1}\). Le point\(P\) possède des coordonnées cartésiennes\((x,y)\). Le segment de ligne reliant l'origine au point\(P\) mesure la distance entre l'origine et le point\(P\) et possède une longueur\(r\). L'angle entre l'axe X positif et le segment de ligne est mesuré\(θ\). Cette observation suggère une correspondance naturelle entre la paire de coordonnées\((x,y)\) et les valeurs\(r\) et\(θ\). Cette correspondance est à la base du système de coordonnées polaires. Notez que chaque point du plan cartésien est associé à deux valeurs (d'où le terme paire ordonnée). Dans le système de coordonnées polaires, deux valeurs sont également associées à chaque point :\(r\) et\(θ\).
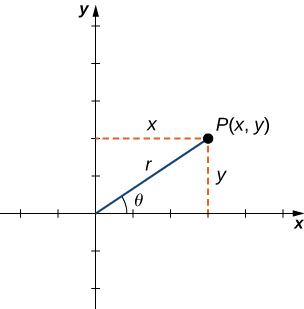
En utilisant la trigonométrie du triangle droit, les équations suivantes sont vraies pour le point\(P\) :
\[\cos θ=\dfrac{x}{r}\text{ so }x=r\cos θ \nonumber \]
\[\sin θ=\dfrac{y}{r}\text{ so }y=r\sin θ. \nonumber \]
En outre,
\[r^2=x^2+y^2 \nonumber \]
et
\[\tan θ=\dfrac{y}{x}. \nonumber \]
Chaque point\((x,y)\) du système de coordonnées cartésien peut donc être représenté sous la forme d'une paire ordonnée\((r,θ)\) dans le système de coordonnées polaires. La première coordonnée est appelée coordonnée radiale et la seconde coordonnée est appelée coordonnée angulaire. Chaque point du plan peut être représenté sous cette forme.
Notez que l'équation\(\tan θ=y/x\) comporte un nombre infini de solutions pour toute paire ordonnée\((x,y)\). Toutefois, si nous limitons les solutions à des valeurs comprises\(2π\) entre\(0\) et, nous pouvons attribuer une solution unique au quadrant dans lequel se\((x,y)\) trouve le point d'origine. Alors la valeur correspondante de\(r\) est positive, donc\(r^2=x^2+y^2\).
Étant donné qu'un point\(P\) du plan possède des coordonnées cartésiennes\((x,y)\) et des coordonnées polaires\((r,θ)\), les formules de conversion suivantes sont vraies :
\[\begin{align} x &=r\cos θ \label{eq1} \\[4pt] y &=r\sin θ \label{eq2}\end{align} \]
et
\[\begin{align} r^2 &= x^2+y^2 \label{eq3}\\[4pt] \tan θ &=\dfrac{y}{x} \label{eq4}\end{align}. \]
Ces formules peuvent être utilisées pour convertir des coordonnées rectangulaires en coordonnées polaires ou des coordonnées polaires en coordonnées rectangulaires. Notez que l'équation \ ref {eq3} est le théorème de Pythagore. (Figurine\(\PageIndex{1}\)).
Convertissez chacun des points suivants en coordonnées polaires.
- \((1,1)\)
- \((−3,4)\)
- \((0,3)\)
- \((5\sqrt{3},−5)\)
Convertissez chacun des points suivants en coordonnées rectangulaires.
- \((3,π/3)\)
- \((2,3π/2)\)
- \((6,−5π/6)\)
Solution
a. Utilisez\(x=1\) et\(y=1\) dans l'équation \ ref {eq3} :
\[\begin{align*} r^2 &=x^2+y^2 \\[4pt] &=1^2+1^2 \\ r &=\sqrt{2} \end{align*} \nonumber \]
et via l'équation \ ref {eq4}
\[\begin{align*} \tan θ &= \dfrac{y}{x} = \dfrac{1}{1}=1 \\[4pt] θ &=\dfrac{π}{4}. \end{align*}\]
Ce point peut donc être représenté sous la\((\sqrt{2},\dfrac{π}{4})\) forme de coordonnées polaires.
b. Utilisez\(x=−3\) et\(y=4\) dans l'équation \ ref {eq3} :
\[\begin{align*} r^2 &= x^2+y^2=(−3)^2+(4)^2 \\[4pt] r&=5 \end{align*}\]
et via l'équation \ ref {eq4}
\(\tan θ=\dfrac{y}{x}=−\dfrac{4}{3}\)
\(θ=\arctan(-\dfrac{4}{3})+π≈2.21.\)
Ce point peut donc être représenté sous la\((5,2.21)\) forme de coordonnées polaires.
c. Utilisez\(x=0\) et\(y=3\) dans l'équation \ ref {eq3} :
\(r^2=x^2+y^2=(3)^2+(0)^2=9+0\)\(r=3\)
et via l'équation \ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{3}{0}\).
L'application directe de la deuxième équation entraîne une division par zéro. Le fait de représenter graphiquement le point\((0,3)\) sur le système de coordonnées rectangulaires indique que le point est situé sur l'axe Y positif. L'angle entre l'axe X positif et l'axe Y positif est\(\dfrac{π}{2}\). Ce point peut donc être représenté sous la\((3,\dfrac{π}{2})\) forme de coordonnées polaires.
d. Utilisez\(x=5\sqrt{3}\) et\(y=−5\) dans l'équation \ ref {eq3} :
\(r^2=x^2+y^2=(5\sqrt{3})^2+(−5)^2=75+25\)
\(r=10\)
et via l'équation \ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{−5}{5\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\)
\(θ=−\dfrac{π}{6}\).
Ce point peut donc être représenté sous la\((10,−\dfrac{π}{6})\) forme de coordonnées polaires.
e. Utilisez\(r=3\) et\(θ=\dfrac{π}{3}\) dans l'équation \ ref {eq1} :
\(x=r\cos θ=3\cos(\dfrac{π}{3})=3(\dfrac{1}{2})=\dfrac{3}{2}\)
et
\(y=r\sin θ=3\sin(\dfrac{π}{3})=3(\dfrac{\sqrt{3}}{2})=\dfrac{3\sqrt{3}}{2}\).
Ce point peut donc être représenté sous forme\((\dfrac{3}{2},\dfrac{3\sqrt{3}}{2})\) de coordonnées rectangulaires.
f. Utilisez\(r=2\) et\(θ=\dfrac{3π}{2}\) dans l'équation \ ref {eq1} :
\(x=r\cos θ=2\cos(\dfrac{3π}{2})=2(0)=0\)
et
\(y=r\sin θ=2\sin(\dfrac{3π}{2})=2(−1)=−2.\)
Ce point peut donc être représenté sous forme\((0,−2)\) de coordonnées rectangulaires.
g. Utilisez\(r=6\) et\(θ=−\dfrac{5π}{6}\) dans l'équation \ ref {eq1} :
\(x=r\cos θ=6\cos(−\dfrac{5π}{6})=6(−\dfrac{\sqrt{3}}{2})=−3\sqrt{3}\)
et
\(y=r\sin θ=6\sin(−\dfrac{5π}{6})=6(−\dfrac{1}{2})=−3\).
Ce point peut donc être représenté sous forme\((−3\sqrt{3},−3)\) de coordonnées rectangulaires.
Convertissez\((−8,−8)\) en coordonnées polaires et\((4,\dfrac{2π}{3})\) en coordonnées rectangulaires.
- Allusion
-
Utilisez l'équation \ ref {eq3} et l'équation \ ref {eq1}. Assurez-vous de vérifier le quadrant lors du calcul\(θ\).
- Réponse
-
\((8\sqrt{2},\dfrac{5π}{4})\)et\((−2,2\sqrt{3})\)
La représentation polaire d'un point n'est pas unique. Par exemple, les coordonnées polaires\((2,\dfrac{π}{3})\) et\((2,\dfrac{7π}{3})\) les deux représentent le point\((1,\sqrt{3})\) dans le système rectangulaire. De plus, la valeur de r peut être négative. Par conséquent, le point avec des coordonnées polaires représente\((−2,\dfrac{4π}{3})\) également le point\((1,\sqrt{3})\) dans le système rectangulaire, comme nous pouvons le voir en utilisant l'équation \ ref {eq1} :
\[x=r\cos θ=−2\cos(\dfrac{4π}{3})=−2(−\dfrac{1}{2})=1 \nonumber \]
et
\[y=r\sin θ=−2\sin(\dfrac{4π}{3})=−2(−\dfrac{\sqrt{3}}{2})=\sqrt{3}. \nonumber \]
Chaque point du plan possède un nombre infini de représentations en coordonnées polaires. Toutefois, chaque point du plan possède une seule représentation dans le système de coordonnées rectangulaires.
Notez que la représentation polaire d'un point dans le plan possède également une interprétation visuelle. En particulier,\(r\) est la distance dirigée entre le point et l'origine et\(θ\) mesure l'angle que fait le segment de ligne entre l'origine et le point avec l'\(x\)axe positif. Les angles positifs sont mesurés dans le sens antihoraire et les angles négatifs sont mesurés dans le sens des aiguilles d'une montre. Le système de coordonnées polaires apparaît sur la figure\(\PageIndex{2}\).
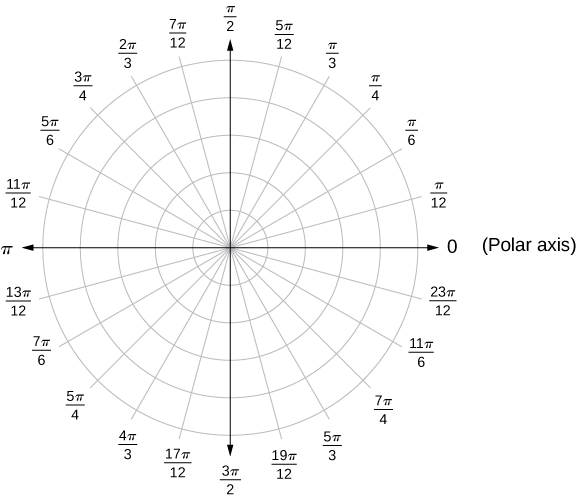
Le segment de droite partant du centre du graphique et allant vers la droite (appelé axe X positif dans le système cartésien) est l'axe polaire. Le point central est le pôle, ou l'origine, du système de coordonnées et correspond à\(r=0\). Le cercle le plus intérieur illustré sur la figure\(\PageIndex{2}\) contient tous les points situés à une distance d'une unité du pôle et est représenté par l'équation\(r=1\). Ensuite, l'ensemble des points\(r=2\) se trouve à 2 unités du pôle, et ainsi de suite. Les segments de ligne émanant du pôle correspondent à des angles fixes. Pour tracer un point dans le système de coordonnées polaires, commencez par l'angle. Si l'angle est positif, mesurez l'angle par rapport à l'axe polaire dans le sens antihoraire. S'il est négatif, mesurez-le dans le sens des aiguilles d'une montre. Si la valeur de r est positive, déplacez cette distance le long du rayon terminal de l'angle. S'il est négatif, déplacez-vous le long du rayon opposé au rayon terminal de l'angle donné.
Tracez chacun des points suivants sur le plan polaire.
- \((2,\dfrac{π}{4})\)
- \((−3,\dfrac{2π}{3})\)
- \((4,\dfrac{5π}{4})\)
Solution
Les trois points sont représentés sur la figure\(\PageIndex{3}\).

\((4,\dfrac{5π}{3})\)Tracez et\((−3,−\dfrac{7π}{2})\) sur le plan polaire.
- Allusion
-
Commencez par\(θ\), puis utilisez\(r\).
- Réponse
-

Courbes polaires
Maintenant que nous savons comment tracer des points dans le système de coordonnées polaires, nous pouvons discuter de la façon de tracer des courbes. Dans le système de coordonnées rectangulaires, nous pouvons représenter graphiquement une fonction\(y=f(x)\) et créer une courbe dans le plan cartésien. De la même manière, nous pouvons tracer une courbe générée par une fonction\(r=f(θ)\).
L'idée générale qui sous-tend la représentation graphique d'une fonction en coordonnées polaires est la même que celle qui sous-tend la représentation graphique d'une fonction en coordonnées rectangulaires. Commencez par une liste de valeurs pour la variable indépendante (\(θ\)dans ce cas) et calculez les valeurs correspondantes de la variable dépendante\(r\). Ce processus génère une liste de paires ordonnées, qui peuvent être tracées dans le système de coordonnées polaires. Enfin, connectez les points et tirez parti des motifs qui peuvent apparaître. La fonction peut être périodique, par exemple, ce qui indique que seul un nombre limité de valeurs pour la variable indépendante est nécessaire.
- Créez un tableau à deux colonnes. La première colonne est pour\(θ\), et la deuxième colonne est pour\(r\).
- Créez une liste de valeurs pour\(θ\).
- Calculez les\(r\) valeurs correspondantes pour chacun\(θ\).
- Tracez chaque paire ordonnée\((r,θ)\) sur les axes de coordonnées.
- Reliez les points et recherchez un motif.
Tracez la courbe définie par la fonction\(r=4\sin θ\). Identifiez la courbe et réécrivez l'équation en coordonnées rectangulaires.
Solution
Comme la fonction est un multiple d'une fonction sinusoïdale, elle est périodique avec un point\(2π\). Utilisez donc des valeurs comprises\(θ\) entre\(0\) et\(2π\). Le résultat des étapes 1 à 3 apparaît dans le tableau suivant. La figure\(\PageIndex{4}\) montre le graphique basé sur ce tableau.
| \(θ\) | \(r=4\sin θ\) | \(θ\) | \(r=4\sin θ\) |
|---|---|---|---|
| \ (θ \) » style="vertical-align:middle ; « >0 | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >0 | \ (θ \) » style="vertical-align:middle ; « >\(π\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >0 |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{6}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >2 | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{7π}{6}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(-2\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{4}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(2\sqrt{2}≈2.8\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{5π}{4}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(−2\sqrt{2}≈−2.8\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{3}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.4\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{4π}{3}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(−2\sqrt{3}≈−3.4\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{π}{2}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >4 | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{3π}{2}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(-4\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{2π}{3}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.4\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{5π}{3}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(−2\sqrt{3}≈−3.4\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{3π}{4}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(2\sqrt{2}≈2.8\) | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{7π}{4}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >\(−2\sqrt{2}≈−2.8\) |
| \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{5π}{6}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >2 | \ (θ \) » style="vertical-align:middle ; « >\(\dfrac{11π}{6}\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >−2 |
| \ (θ \) » style="vertical-align:middle ; « > | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « > | \ (θ \) » style="vertical-align:middle ; « >\(2π\) | \ (r=4 \ sin θ \) » style="vertical-align:middle ; « >0 |
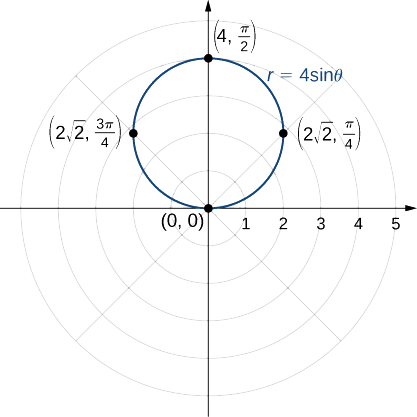
C'est le graphique d'un cercle. L'équation\(r=4\sin θ\) peut être convertie en coordonnées rectangulaires en multipliant d'abord les deux côtés par\(r\). Cela donne l'équation\(r^2=4r\sin θ.\) Ensuite, utilisez les faits que\(r^2=x^2+y^2\) et\(y=r\sin θ\). Cela donne\(x^2+y^2=4y\). Pour mettre cette équation sous forme standard, soustrayez-la\(4y\) des deux côtés de l'équation et complétez le carré :
\[\begin{align*} x^2+y^2−4y &= 0 \\[4pt] x^2+(y^2−4y) &= 0 \\[4pt] x^2+(y^2−4y+4) &= 0+4 \\[4pt] x^2+(y−2)^2&=4 \end{align*}\]
Il s'agit de l'équation d'un cercle de rayon 2 et de centre\((0,2)\) dans le système de coordonnées rectangulaires.
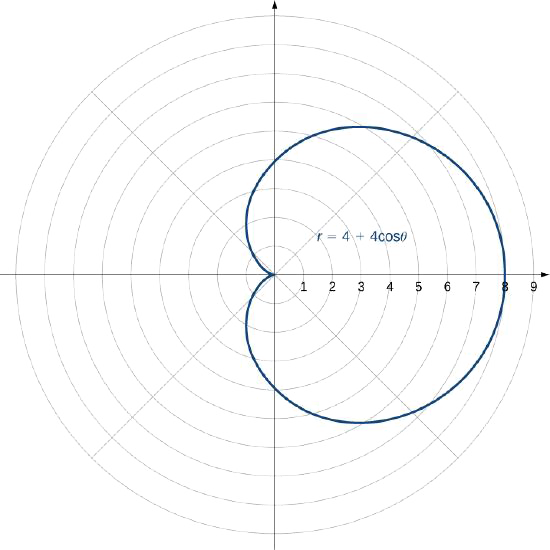
Créez un graphique de la courbe définie par la fonction\(r=4+4\cos θ\).
- Allusion
-
Suivez la stratégie de résolution de problèmes pour créer un graphique en coordonnées polaires.
- Réponse
-
Le nom de cette forme est un cardioïde, que nous étudierons plus loin dans cette section.
Le graphique de l'exemple\(\PageIndex{3}\) était celui d'un cercle. L'équation du cercle peut être transformée en coordonnées rectangulaires à l'aide des formules de transformation des coordonnées de l'équation \ ref {eq1}. L'exemple\(\PageIndex{4}\) donne d'autres exemples de fonctions permettant de transformer des coordonnées polaires en coordonnées rectangulaires.
Réécrivez chacune des équations suivantes en coordonnées rectangulaires et identifiez le graphe.
- \(θ=\dfrac{π}{3}\)
- \(r=3\)
- \(r=6\cos θ−8\sin θ\)
Solution :
a. Prenez la tangente des deux côtés. Cela donne\(\tan θ=\tan(π/3)=\sqrt{3}\). Puisque\(\tan θ=y/x\) nous pouvons remplacer le côté gauche de cette équation par\(y/x\). Cela donne\(y/x=\sqrt{3}\), qui peut être réécrit comme\(y=x\sqrt{3}\). Il s'agit de l'équation d'une droite passant par l'origine avec une pente\(\sqrt{3}\). En général, toute équation polaire de cette forme\(θ=K\) représente une ligne droite passant par le pôle avec une pente égale à\(\tan K\).
b. Tout d'abord, mettez les deux côtés de l'équation au carré. Cela permet à\(r^2=9.\) Next de le\(r^2\) remplacer par\(x^2+y^2\). Cela donne l'équation\(x^2+y^2=9\), qui est l'équation d'un cercle centré à l'origine avec un rayon 3. En général, toute équation polaire de la forme\(r=k\) où k est une constante positive représente un cercle de rayon k centré sur l'origine. (Remarque : lors de la mise au carré des deux côtés d'une équation, il est possible d'introduire de nouveaux points involontairement. Cela doit toujours être pris en considération. Toutefois, dans ce cas, nous n'introduisons pas de nouveaux points. Par exemple,\((−3,\dfrac{π}{3})\) c'est le même point que\((3,\dfrac{4π}{3})\).)
c. Multipliez les deux côtés de l'équation par\(r\). Cela conduit à\(r^2=6r\cos θ−8r\sin θ\). Ensuite, utilisez les formules
\(r^2=x^2+y^2,x=r\cos θ,y=r\sin θ.\)
Cela donne
\(r^2=6(r\cos θ)−8(r\sin θ)\)
\(x^2+y^2=6x−8y.\)
Pour mettre cette équation sous forme standard, déplacez d'abord les variables du côté droit de l'équation vers le côté gauche, puis complétez le carré.
\(x^2+y^2=6x−8y\)
\(x^2−6x+y^2+8y=0\)
\((x^2−6x)+(y^2+8y)=0\)
\((x^2−6x+9)+(y^2+8y+16)=9+16\)
\((x−3)^2+(y+4)^2=25.\)
Il s'agit de l'équation d'un cercle dont le centre\((3,−4)\) et le rayon sont 5. Remarquez que le cercle passe par l'origine puisque le centre se trouve à 5 unités.
Réécrivez l'équation\(r=\sec θ\tan θ\) en coordonnées rectangulaires et identifiez son graphe.
- Allusion
-
Convertissez en sinus et en cosinus, puis multipliez les deux côtés par le cosinus.
- Réponse
-
\(y=x^2\), qui est l'équation d'une parabole s'ouvrant vers le haut.
Nous avons maintenant vu plusieurs exemples de dessin de graphes de courbes définies par des équations polaires. Un résumé de certaines courbes courantes est donné dans les tableaux ci-dessous. Dans chaque équation, a et b sont des constantes arbitraires.
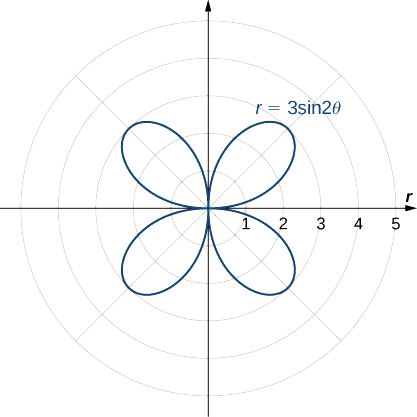
Un cardioïde est un cas particulier de limaçon (prononcé « lee-mah-son »), dans lequel\(a=b\) ou\(a=−b\). La rose est une courbe très intéressante. Notez que le graphe de\(r=3\sin 2θ\) comporte quatre pétales. Cependant, le graphique de\(r=3\sin 3θ\) comporte trois pétales, comme indiqué.
Si le coefficient de\(θ\) est pair, le graphique comporte deux fois plus de pétales que le coefficient. Si le coefficient de\(θ\) est impair, le nombre de pétales est égal au coefficient. Nous vous encourageons à découvrir pourquoi cela se produit. Des graphes encore plus intéressants apparaissent lorsque le coefficient de n'\(θ\)est pas un entier. Par exemple, si elle est rationnelle, la courbe est fermée, c'est-à-dire qu'elle finit par se terminer là où elle a commencé (Figure\(\PageIndex{8a}\)). Toutefois, si le coefficient est irrationnel, la courbe ne se ferme jamais (Figure\(\PageIndex{8b}\)). Bien qu'il puisse sembler que la courbe est fermée, un examen plus approfondi révèle que les pétales situés juste au-dessus de l'axe x positif sont légèrement plus épais. C'est parce que le pétale ne correspond pas tout à fait au point de départ.
Puisque la courbe définie par le graphique de\(r=3\sin(πθ)\) ne jamais se fermer, la courbe représentée sur la figure n'\(\PageIndex{8b}\)est qu'une représentation partielle. En fait, il s'agit d'un exemple de courbe de remplissage d'espace. Une courbe remplissant l'espace est une courbe qui occupe en fait un sous-ensemble bidimensionnel du plan réel. Dans ce cas, la courbe occupe le cercle de rayon 3 centré à l'origine.
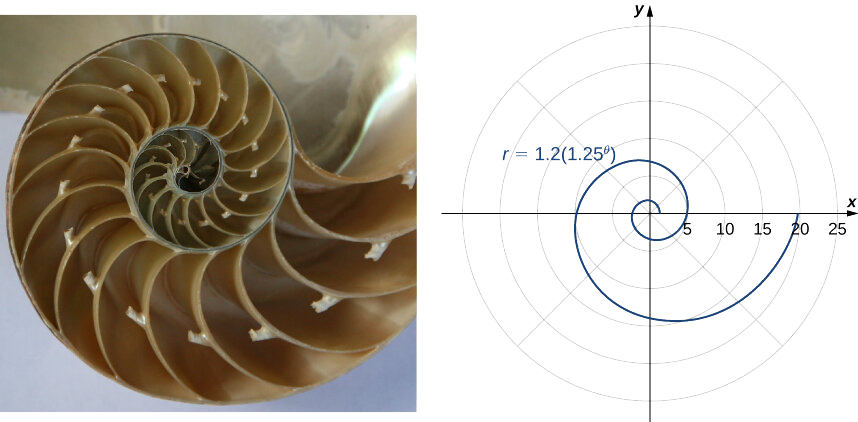
Souvenez-vous du nautilus chambré introduit dans le prélude du chapitre. Cette créature affiche une spirale lorsque la moitié de sa carapace extérieure est coupée. Il est possible de décrire une spirale à l'aide de coordonnées rectangulaires. La figure\(\PageIndex{9}\) montre une spirale en coordonnées rectangulaires. Comment décrire mathématiquement cette courbe ?
Solution
Lorsque le point P fait le tour de la spirale dans le sens antihoraire, sa distance d par rapport à l'origine augmente. Supposons que la distance d est un multiple k constant de l'angle\(θ\) que fait le segment de droite OP avec l'axe X positif. Par conséquent\(d(P,O)=kθ\), où en\(O\) est l'origine. Utilisez maintenant la formule de distance et un peu de trigonométrie :
\(d(P,O)=kθ\)
\(\sqrt{(x−0)^2+(y−0)^2}=k\arctan(\dfrac{y}{x})\)
\(\sqrt{x^2+y^2}=k\arctan(\dfrac{y}{x})\)
\(\arctan(\dfrac{y}{x})=\dfrac{\sqrt{x^2+y^2}}{k}\)
\(y=x\tan(\dfrac{\sqrt{x^2+y^2}}{k})\).
Bien que cette équation décrit la spirale, il n'est pas possible de la résoudre directement pour x ou y. Cependant, si nous utilisons des coordonnées polaires, l'équation devient beaucoup plus simple. En particulier\(d(P,O)=r\), et\(θ\) est la deuxième coordonnée. Par conséquent, l'équation de la spirale devient\(r=kθ\). Notez que lorsque\(θ=0\) nous l'avons également\(r=0\), la spirale émane de l'origine. Nous pouvons supprimer cette restriction en ajoutant une constante à l'équation. Ensuite, l'équation de la spirale devient\(r=a+kθ\) pour les constantes arbitraires\(a\) et\(k\). C'est ce que l'on appelle une spirale d'Archimède, d'après le mathématicien grec Archimède.
Un autre type de spirale est la spirale logarithmique, décrite par la fonction\(r=a⋅b^θ\). Un graphique de la fonction\(r=1.2(1.25^θ)\) est présenté dans la figure\(\PageIndex{10}\). Cette spirale décrit la forme de la coque du nautilus chambré.
Supposons qu'une courbe soit décrite dans le système de coordonnées polaires via la fonction\(r=f(θ)\). Puisque nous avons des formules de conversion de coordonnées polaires en coordonnées rectangulaires données par
\[x=r\cos θ \nonumber \]
\[y=r\sin θ \nonumber \],
il est possible de réécrire ces formules à l'aide de la fonction
\[x=f(θ)\cos θ \nonumber \]
\[y=f(θ)\sin θ. \nonumber \]
Cette étape permet de paramétrer la courbe en coordonnées rectangulaires en utilisant\(θ\) comme paramètre. Par exemple, la formule en spirale\(r=a+bθ\) de la figure devient
\[x=(a+bθ)\cos θ \nonumber \]
\[y=(a+bθ)\sin θ. \nonumber \]
Laisser\(θ\) aller de\(−∞\) à\(∞\) génère toute la spirale.
Symétrie en coordonnées polaires
Lorsque nous étudions la symétrie des fonctions en coordonnées rectangulaires (c'est-à-dire dans la forme\(y=f(x)\)), nous parlons de symétrie par rapport à l'axe y et de symétrie par rapport à l'origine. En particulier, si\(f(−x)=f(x)\) pour tous se situent\(x\) dans le domaine de\(f\), alors\(f\) est une fonction paire et son graphe est symétrique par rapport à l'axe y. Si\(f(−x)=−f(x)\) pour tout x dans le domaine de\(f\), alors f est une fonction impaire et son graphe est symétrique par rapport à l'origine. En déterminant les types de symétrie d'un graphe, nous pouvons en apprendre davantage sur la forme et l'apparence du graphe. La symétrie peut également révéler d'autres propriétés de la fonction qui génère le graphe. La symétrie des courbes polaires fonctionne de la même manière.
Prenons l'exemple d'une courbe générée par la fonction\(r=f(θ)\) en coordonnées polaires.
- La courbe est symétrique par rapport à l'axe polaire si, pour chaque point\((r,θ)\) du graphique, le point\((r,−θ)\) se trouve également sur le graphique. De même, l'équation\(r=f(θ)\) reste inchangée en\(θ\) remplaçant par\(−θ\).
- La courbe est symétrique par rapport au pôle si, pour chaque point\((r,θ)\) du graphique, le point\((r,π+θ)\) se trouve également sur le graphique. De même, l'équation reste\(r=f(θ)\) inchangée en cas de remplacement\(r\) par\(−r\), ou\(θ\) par\(π+θ.\)
- La courbe est symétrique par rapport à la ligne verticale\(θ=\dfrac{π}{2}\) si, pour chaque point\((r,θ)\) du graphique, le point\((r,π−θ)\) se trouve également sur le graphique. De même, l'équation\(r=f(θ)\) reste inchangée lorsqu'elle\(θ\) est remplacée par\(π−θ\).
Le tableau suivant présente des exemples de chaque type de symétrie.
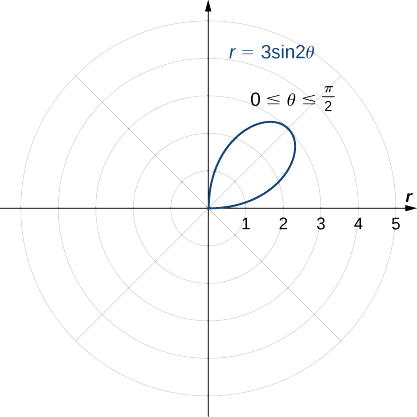
Trouvez la symétrie de la rose définie par l'équation\(r=3\sin(2θ)\) et créez un graphique.
Solution
Supposons que le point\((r,θ)\) se trouve sur le graphique de\(r=3\sin(2θ).\)
i. Pour vérifier la symétrie autour de l'axe polaire, essayez d'abord de\(θ\) remplacer par\(−θ\). Cela donne\(r=3\sin(2(−θ))=−3\sin(2θ)\). Comme cela modifie l'équation initiale, ce test n'est pas satisfait. Cependant, en revenant à l'équation initiale et en la\(r\) remplaçant par\(−r\) et\(θ\) par\(π−θ\) les rendements
\[ \begin{align*} −r&=3\sin(2(π−θ)) \\[4pt] −r &=3\sin(2π−2θ) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3\sin2θ. \end{align*}\]
Multiplier les deux côtés de cette équation par\(−1\) donne\(r=3\sin 2θ\), ce qui est l'équation d'origine. Cela montre que le graphe est symétrique par rapport à l'axe polaire.
ii. Pour vérifier la symétrie par rapport au pôle, remplacez d'abord\(r\) par\(−r\), qui cède\(−r=3\sin(2θ)\). Multiplier les deux côtés par\(−1\) donne\(r=−3\sin(2θ)\), ce qui ne correspond pas à l'équation initiale. L'équation ne passe donc pas le test de cette symétrie. Cependant, en revenant à l'équation d'origine et en la\(θ\) remplaçant\(θ+π\) par
\[ \begin{align*} r&=3\sin(2(θ+π)) \\[4pt] &=3\sin(2θ+2π) \\[4pt] &=3(\sin 2θ \cos 2π + \cos 2θ \sin 2π) \\[4pt] &=3\sin 2θ. \end{align*}\]
Comme cela correspond à l'équation initiale, le graphique est symétrique par rapport au pôle.
iii. Pour tester la symétrie par rapport à la ligne verticale\(θ=\dfrac{π}{2}\), remplacez d'abord\(r\) par\(−r\) et\(θ\) par\(−θ\).
\[ \begin{align*} −r &=3\sin(2(−θ)) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3 \sin 2θ. \end{align*}\]
Multiplier les deux côtés de cette équation par\(−1\) donne\(r=3\sin 2θ\), ce qui est l'équation d'origine. Le graphique est donc symétrique par rapport à la ligne verticale\(θ=\dfrac{π}{2}\).
Ce graphique présente une symétrie par rapport à l'axe polaire, à l'origine et à la ligne verticale passant par le pôle. Pour représenter graphiquement la fonction, tabulez les valeurs comprises\(θ\) entre\(0\)\(π/2\) et puis reflétez le graphique obtenu.
| 0 | 0 |
| \(\dfrac{π}{6}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{4}\) | 3 |
| \(\dfrac{π}{3}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{2}\) | 0 |
On obtient ainsi un pétale de rose, comme le montre le graphique suivant.
La réflexion de cette image dans les trois autres quadrants donne le graphique complet tel qu'illustré.
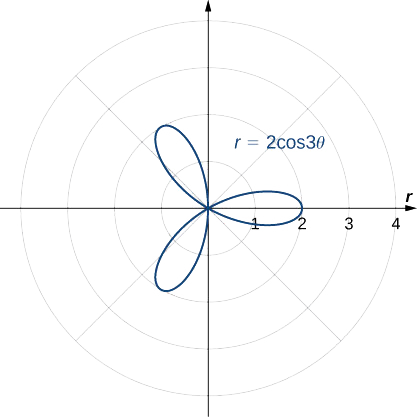
Déterminez la symétrie du graphe déterminée par l'équation\(r=2\cos(3θ)\) et créez un graphique.
- Allusion
-
Note d'utilisation.
- Réponse
-
Symétrique par rapport à l'axe polaire.
Concepts clés
- Le système de coordonnées polaires fournit une autre méthode pour localiser des points dans le plan.
- Convertissez des points entre des coordonnées rectangulaires et polaires à l'aide des formules
\[x=r\cos θ \text{ and } y=r\sin θ \nonumber \]
et
\[r=\sqrt{x^2+y^2} \text{ and} \tan θ=\dfrac{y}{x}. \nonumber \]
- Pour esquisser une courbe polaire à partir d'une fonction polaire donnée, créez un tableau de valeurs et tirez parti des propriétés périodiques.
- Utilisez les formules de conversion pour convertir des équations entre des coordonnées rectangulaires et des coordonnées polaires.
- Identifiez la symétrie des courbes polaires, qui peut se produire par le biais du pôle, de l'axe horizontal ou de l'axe vertical.
Lexique
- coordonnée angulaire
- \(θ\)l'angle formé par un segment de droite reliant l'origine à un point du système de coordonnées polaires avec l'axe radial (x) positif, mesuré dans le sens antihoraire
- cardioïde
- une courbe plane tracée par un point sur le périmètre d'un cercle qui tourne autour d'un cercle fixe de même rayon ; l'équation d'un cardioïde est\(r=a(1+\sin θ)\) ou\(r=a(1+\cos θ)\)
- limaçon
- le graphe de l'équation\(r=a+b\sin θ\) ou\(r=a+b\cos θ.\) Si\(a=b\) alors le graphe est un cardioïde
- axe polaire
- l'axe horizontal dans le système de coordonnées polaires correspondant à\(r≥0\)
- système de coordonnées polaires
- un système de localisation de points dans le plan. Les coordonnées sont\(r\) les coordonnées radiales et\(θ\) les coordonnées angulaires
- équation polaire
- une équation ou une fonction reliant la coordonnée radiale à la coordonnée angulaire dans le système de coordonnées polaires
- poteau
- le point central du système de coordonnées polaires, équivalent à l'origine d'un système cartésien
- coordonnée radiale
- \(r\)la coordonnée du système de coordonnées polaires qui mesure la distance entre un point du plan et le pôle
- rose
- graphique de l'équation polaire\(r=a\cos 2θ\) ou\(r=a\sin 2θ\) pour une constante positive\(a\)
- courbe de remplissage d'espace
- une courbe qui occupe complètement un sous-ensemble bidimensionnel du plan réel


