11.2 : Calcul des courbes paramétriques

Last updated
Save as PDF

Page ID: 197253

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Déterminez les dérivées et les équations des tangentes pour les courbes paramétriques.
Trouvez l'aire sous une courbe paramétrique.
Utilisez l'équation pour la longueur de l'arc d'une courbe paramétrique.
Appliquez la formule de la surface à un volume généré par une courbe paramétrique.

Maintenant que nous avons introduit le concept de courbe paramétrée, la prochaine étape consiste à apprendre à utiliser ce concept dans le contexte du calcul. Par exemple, si nous connaissons le paramétrage d'une courbe donnée, est-il possible de calculer la pente d'une tangente à la courbe ? Qu'en est-il de la longueur de l'arc de la courbe ? Ou la zone située sous la courbe ?

Autre scénario : Supposons que nous souhaitions représenter l'emplacement d'une balle de baseball une fois que la balle a quitté la main d'un lanceur. Si la position de la balle est représentée par la courbe plane$(x(t),y(t))$, nous devrions pouvoir utiliser le calcul pour déterminer la vitesse de la balle à tout moment. De plus, nous devrions être en mesure de calculer la distance parcourue par cette balle en fonction du temps.

Les dérivées des équations paramétriques

Nous commençons par nous demander comment calculer la pente d'une droite tangente à une courbe paramétrique en un point. Considérez la courbe plane définie par les équations paramétriques

\[\begin{align} x(t) &=2t+3 \label{eq1} \\ y(t) &=3t−4 \label{eq2} \end{align} \]

au sein de$−2≤t≤3$.

Le graphique de cette courbe apparaît sur la figure$\PageIndex{1}$. Il s'agit d'un segment de ligne commençant à$(−1,−10)$ et se terminant à$(9,5).$

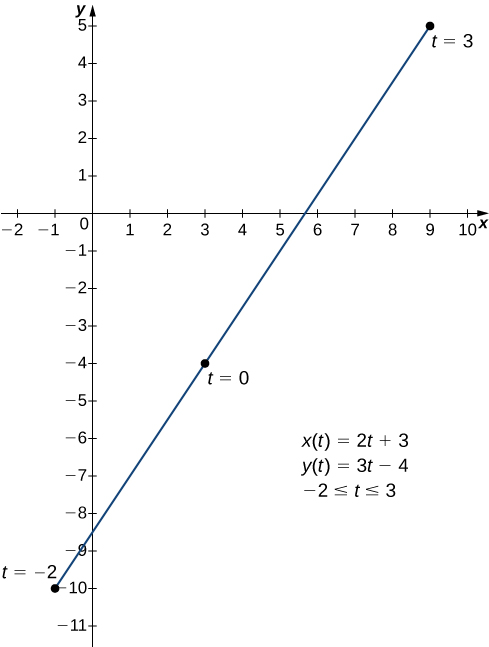
Une ligne droite allant de (−1, −10) à (9, 5). Le point (−1, −10) est marqué t = −2, le point (3, −4) est marqué t = 0 et le point (9, 5) est marqué t = 3. Trois équations sont marquées : x (t) = 2t + 3, y (t) = 3t — 4 et −2 ≤ t ≤ 3 — Figure$\PageIndex{1}$ : Graphique du segment de droite décrit par les équations paramétriques données.

Nous pouvons éliminer le paramètre en résolvant d'abord l'équation \ ref {eq1} pour$t$ :

$x(t)=2t+3$

$x−3=2t$

$t=\dfrac{x−3}{2}$.

En le remplaçant par$y(t)$ (Équation \ ref {eq2}), nous obtenons

$y(t)=3t−4$

$y=3\left(\dfrac{x−3}{2}\right)−4$

$y=\dfrac{3x}{2}−\dfrac{9}{2}−4$

$y=\dfrac{3x}{2}−\dfrac{17}{2}$.

La pente de cette ligne est donnée par$\dfrac{dy}{dx}=\dfrac{3}{2}$. Ensuite, nous calculons$x′(t)$ et$y′(t)$. Cela donne$x′(t)=2$ et$y′(t)=3$. Remarquez que

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{3}{2}. \nonumber \]

Ce n'est pas un hasard, comme indiqué dans le théorème suivant.

Dérivée des équations paramétriques

Considérez la courbe plane définie par les équations paramétriques$x=x(t)$ et$y=y(t)$. Supposons cela$x′(t)$ et$y′(t)$ existez, et supposez que$x′(t)≠0$. Ensuite, la dérivée$\dfrac{dy}{dx}$ est donnée par

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)}. \label{paraD} \]

Une preuve

Ce théorème peut être prouvé à l'aide de la règle de chaîne. Supposons en particulier que le paramètre$t$ puisse être éliminé, ce qui donne une fonction dérivable$y=F(x)$. Ensuite,$y(t)=F(x(t)).$ la différenciation des deux côtés de cette équation à l'aide de la règle de chaîne donne

\[y′(t)=F′\big(x(t)\big)x′(t), \nonumber \]

donc

\[F′\big(x(t)\big)=\dfrac{y′(t)}{x′(t)}. \nonumber \]

Mais$F′\big(x(t)\big)=\dfrac{dy}{dx}$, ce qui prouve le théorème.

□

L'équation \ ref {ParAd} peut être utilisée pour calculer des dérivées de courbes planes, ainsi que des points critiques. Rappelez-vous qu'un point critique d'une fonction dérivable$y=f(x)$ est un point$x=x_0$ tel qu'il existe$f′(x_0)=0$ ou$f′(x_0)$ n'existe pas. L'équation \ ref {ParAd} donne une formule pour la pente d'une droite tangente à une courbe définie de manière paramétrique, que la courbe puisse être décrite par une fonction$y=f(x)$ ou non.

Exemple$\PageIndex{1}$: Finding the Derivative of a Parametric Curve

Calculez la dérivée$\dfrac{dy}{dx}$ pour chacune des courbes planes définies de manière paramétrique suivantes et localisez les points critiques sur leurs graphes respectifs.

$x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4$
$x(t)=2t+1, \quad y(t)=t^3−3t+4, \quad\text{for }−2≤t≤2$
$x(t)=5\cos t, \quad y(t)=5\sin t, \quad\text{for }0≤t≤2π$

Solution

a. Pour appliquer l'équation \ ref {ParAd}, commencez par calculer$x′(t)$ et$y′(t)$ :

$x′(t)=2t$

$y′(t)=2$.

Ensuite, remplacez-les dans l'équation :

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{2}{2t}$

$\dfrac{dy}{dx}=\dfrac{1}{t}$.

Cette dérivée n'est pas définie quand$t=0$. Calculer$x(0)$$x(0)=(0)^2−3=−3$ et$y(0)$ donne et$y(0)=2(0)−1=−1$, qui correspond au point$(−3,−1)$ sur le graphique. Le graphique de cette courbe est une parabole s'ouvrant vers la droite, et le point$(−3,−1)$ est son sommet, comme indiqué.

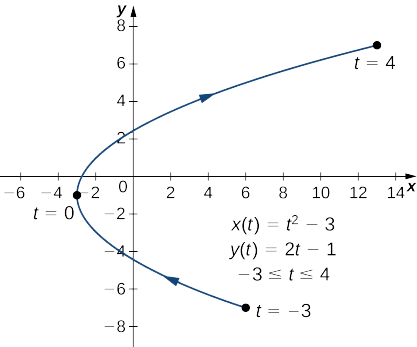
Une ligne courbe allant de (6, −7) à (−3, −1) à (13, 7) avec une flèche pointant dans cet ordre. Le point (6, −7) est marqué t = −3, le point (−3, −1) est marqué t = 0 et le point (13, 7) est marqué t = 4. Trois équations sont également écrites sur le graphique : x (t) = t2 − 3, y (t) = 2t − 1 et −3 ≤ t ≤ 4. — Figure$\PageIndex{2}$ : Graphique de la parabole décrite par des équations paramétriques dans la partie a.

b. Pour appliquer l'équation \ ref {ParAd}, commencez par calculer$x′(t)$ et$y′(t)$ :

$x′(t)=2$

$y′(t)=3t^2−3$.

Ensuite, remplacez-les dans l'équation :

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{3t^2−3}{2}$.

Cette dérivée est nulle lorsque$t=±1$. Lorsque$t=−1$ nous avons

$x(−1)=2(−1)+1=−1$et$y(−1)=(−1)^3−3(−1)+4=−1+3+4=6$,

qui correspond au point$(−1,6)$ sur le graphique. Lorsque$t=1$ nous avons

$x(1)=2(1)+1=3$et$y(1)=(1)^3−3(1)+4=1−3+4=2,$

qui correspond au point$(3,2)$ sur le graphique. Le point$(3,2)$ est un minimum relatif et le point$(−1,6)$ est un maximum relatif, comme le montre le graphique suivant.

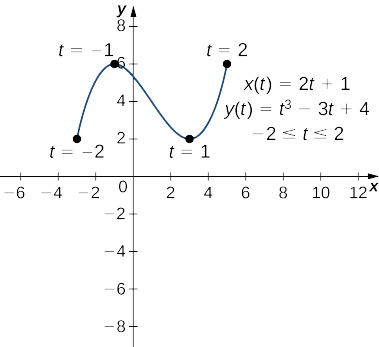
Une courbe vaguement sinusoïdale allant de (−3, 2) à (-1, 6) et (3, 2) à (5, 6). Le point (−3, 2) est marqué t = −2, le point (−1, 6) est marqué t = −1, le point (3, 2) est marqué t = 1 et le point (5, 6) est marqué t = 2. Trois équations sont également écrites sur le graphique : x (t) = 2t + 1, y (t) = t3 — 3t + 4 et −2 ≤ t ≤ 2. — Figure$\PageIndex{3}$ : Graphique de la courbe décrite par des équations paramétriques dans la partie b.

c. Pour appliquer l'équation \ ref {ParAd}, commencez par calculer$x′(t)$ et$y′(t)$ :

$x′(t)=−5\sin t$

$y′(t)=5\cos t.$

Ensuite, remplacez-les dans l'équation :

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{5\cos t}{−5\sin t}$

$\dfrac{dy}{dx}=−\cot t.$

Cette dérivée est nulle$\cos t=0$ et n'est pas définie lorsque$\sin t=0.$ Cela donne$t=0,\dfrac{π}{2},π,\dfrac{3π}{2},$ et$2π$ en tant que points critiques pour t. En remplaçant chacun d'eux par$x(t)$ et$y(t)$, nous obtenons

$t$	$x(t)$	$y(t)$
\ (t \) » style="vertical-align:middle ; « >0	\ (x (t) \) » style="vertical-align:middle ; « >5	\ (y (t) \) » style="vertical-align:middle ; « >0
\ (t \) » style="vertical-align:middle ; « >$\dfrac{π}{2}$	\ (x (t) \) » style="vertical-align:middle ; « >0	\ (y (t) \) » style="vertical-align:middle ; « >5
\ (t \) » style="vertical-align:middle ; « >$π$	\ (x (t) \) » style="vertical-align:middle ; « >−5	\ (y (t) \) » style="vertical-align:middle ; « >0
\ (t \) » style="vertical-align:middle ; « >$\dfrac{3π}{2}$	\ (x (t) \) » style="vertical-align:middle ; « >0	\ (y (t) \) » style="vertical-align:middle ; « >−5
\ (t \) » style="vertical-align:middle ; « >$2π$	\ (x (t) \) » style="vertical-align:middle ; « >5	\ (y (t) \) » style="vertical-align:middle ; « >0

Ces points correspondent aux côtés, au haut et au bas du cercle représenté par les équations paramétriques (Figure$\PageIndex{4}$). Sur les bords gauche et droit du cercle, la dérivée n'est pas définie, et en haut et en bas, la dérivée est égale à zéro.

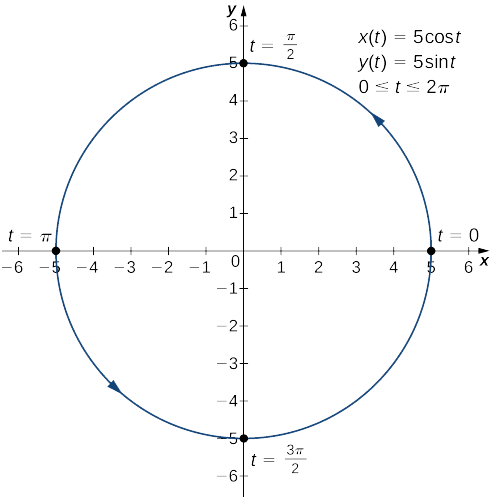
Un cercle de rayon 5 centré sur l'origine est représenté par une flèche dans le sens antihoraire. Le point (5, 0) est marqué t = 0, le point (0, 5) est marqué t = π/2, le point (−5, 0) est marqué t = π et le point (0, −5) est marqué t = 3π/2. Trois équations sont également écrites sur le graphique : x (t) = 5 cos (t), y (t) = 5 sin (t) et 0 ≤ t ≤ 2π. — Figure$\PageIndex{4}$ : Graphique de la courbe décrite par des équations paramétriques dans la partie c.

Exercice$\PageIndex{1}$

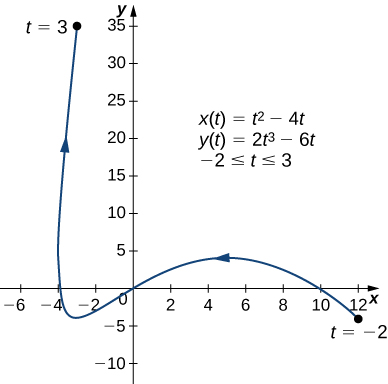
Calculer la dérivée$dy/dx$ de la courbe plane définie par les équations

\[x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3 \nonumber \]

et localisez tous les points critiques sur son graphique.

Allusion: Calculez$x′(t)$$y′(t)$ et utilisez l'équation \ ref {ParAd}.

Réponse

$x′(t)=2t−4$et$y′(t)=6t^2−6$ donc$\dfrac{dy}{dx}=\dfrac{6t^2−6}{2t−4}=\dfrac{3t^2−3}{t−2}$.

Cette expression n'est pas définie quand$t=2$ et est égale à zéro quand$t=±1$.

$Une courbe allant de (12, −4) à l'origine et (−4, 0) à (−3, 36) avec des flèches dans cet ordre. Le point (12, −4) est marqué t = −2 et le point (−3, 36) est marqué t = 3. Trois équations sont également écrites sur le graphique : x (t) = t2 — 4t, y (t) = 2t3 — 6t et −2 ≤ t ≤ 3.$

Exemple$\PageIndex{2}$: Finding a Tangent Line

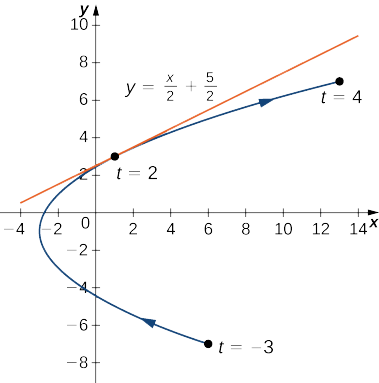
Trouvez l'équation de la tangente à la courbe définie par les équations

\[x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4 \nonumber \]

quand$t=2$.

Solution

Déterminez d'abord la pente de la tangente à l'aide de l'équation \ ref {ParAd}, ce qui signifie calculer$x′(t)$ et$y′(t)$ :

$x′(t)=2t$

$y′(t)=2$.

Ensuite, remplacez-les dans l'équation :

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{2}{2t}$

$\dfrac{dy}{dx}=\dfrac{1}{t}$.

Quand$t=2, \dfrac{dy}{dx}=\dfrac{1}{2}$, c'est donc la pente de la tangente. Calculer$x(2)$ et$y(2)$ donner

$x(2)=(2)^2−3=1$et$y(2)=2(2)−1=3$,

qui correspond au point$(1,3)$ du graphique (Figure$\PageIndex{5}$). Utilisez maintenant la forme de pente ponctuelle de l'équation d'une droite pour trouver l'équation de la tangente :

$y−y_0=m(x−x_0)$

$y−3=\dfrac{1}{2}(x−1)$

$y−3=\dfrac{1}{2}x−\dfrac{1}{2}$

$y=\dfrac{1}{2}x+\dfrac{5}{2}$.

Exercice$\PageIndex{2}$

Trouvez l'équation de la tangente à la courbe définie par les équations

$x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤6$quand$t=5$.

Allusion: Calculez$x′(t)$$y′(t)$ et utilisez l'équation \ ref {ParAd}.

Réponse: L'équation de la tangente est$y=24x+100.$

Produits dérivés du second ordre

Notre prochain objectif est de voir comment prendre la dérivée seconde d'une fonction définie de manière paramétrique. La dérivée seconde d'une fonction$y=f(x)$ est définie comme étant la dérivée de la première, c'est-à-dire que

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left[\dfrac{dy}{dx}\right]. \label{eqD2} \]

Depuis

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}, \nonumber \]

nous pouvons remplacer les deux$y$ côtés de l'équation \ ref {eQD2} par$\dfrac{dy}{dx}$. Cela nous donne

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx} \left(\dfrac{dy}{dx} \right)=\dfrac{(d/dt)(dy/dx)}{dx/dt}.\label{paraD2} \]

Si nous savons$dy/dx$ en fonction de$t$, alors cette formule est simple à appliquer

Exemple$\PageIndex{3}$: Finding a Second Derivative

Calculer la dérivée seconde$d^2y/dx^2$ de la courbe plane définie par les équations paramétriques$x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4.$

Solution

D'après Example,$\PageIndex{1}$ nous le savons$\dfrac{dy}{dx}=\dfrac{2}{2t}=\dfrac{1}{t}$. En utilisant l'équation \ ref {ParaD2}, nous obtenons

$\dfrac{d^2y}{dx^2}=\dfrac{(d/dt)(dy/dx)}{dx/dt}=\dfrac{(d/dt)(1/t)}{2t}=\dfrac{−t^{−2}}{2t}=−\dfrac{1}{2t^3}$.

Exercice$\PageIndex{3}$

Calculer la dérivée seconde$d^2y/dx^2$ de la courbe plane définie par les équations

$x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3$

et localisez tous les points critiques sur son graphique.

Allusion: Commencez par la solution de l'exercice précédent et utilisez l'équation \ ref {ParAd2}.

Réponse: $\dfrac{d^2y}{dx^2}=\dfrac{3t^2−12t+3}{2(t−2)^3}$. Points critiques$(5,4),\, (−3,−4)$, et$(−4,6).$

Intégrales impliquant des équations paramétriques

Maintenant que nous avons vu comment calculer la dérivée d'une courbe plane, la question suivante est la suivante : Comment trouver l'aire sous une courbe définie de manière paramétrique ? Rappelons la cycloïde définie par ces équations paramétriques

\[ \begin{align*} x(t) &=t−\sin t \\[4pt] y(t) &=1−\cos t. \end{align*}\]

Supposons que nous souhaitions trouver l'aire de la région ombrée dans le graphique suivant.

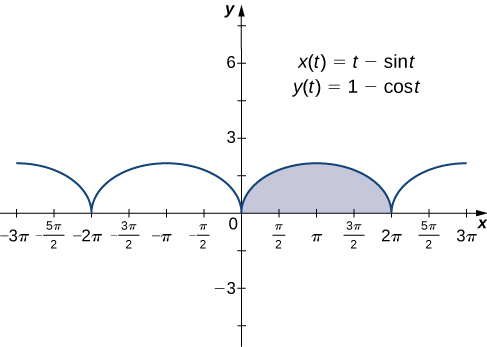
Série de demi-cercles dessinés au-dessus de l'axe x, les points d'intersection x étant des multiples de 2π. Le demi-cercle entre 0 et 2π est surligné. Deux équations sont également écrites sur le graphique : x (t) = t — sin (t) et y (t) = 1 — cos (t). — Figure$\PageIndex{6}$ : Diagramme d'une cycloïde avec l'arc$[0,2π]$ surligné.

Pour dériver une formule pour l'aire sous la courbe définie par les fonctions

\[\begin{align*} x &=x(t) \\[4pt] y &=y(t) \end{align*}\]

où$a≤t≤b$.

Nous supposons que$x(t)$ c'est dérivable et commençons par une répartition égale de l'intervalle$a≤t≤b$. Supposons$t_0=a<t_1<t_2<⋯<t_n=b$ et considérez le graphique suivant.

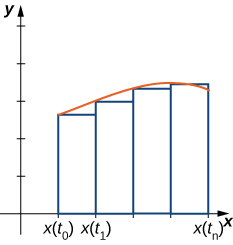
Une ligne courbe est tracée dans le premier quadrant. En dessous se trouvent une série de rectangles marqués qui commencent par l'axe x et atteignent la ligne courbe ; la hauteur du rectangle est déterminée par l'emplacement de la ligne courbe au point le plus à gauche du rectangle. Ces lignes sont notées x (t0), x (t1),..., x (tn). — Figure$\PageIndex{7}$ : Approximation de l'aire sous une courbe définie de manière paramétrique.

Nous utilisons des rectangles pour approximer la zone située sous la courbe. La hauteur d'un rectangle typique dans cette paramétrisation correspond$y(x(\bar{t_i}))$ à une certaine valeur$\bar{t_i}$ dans le$i^\text{th}$ sous-intervalle, et la largeur peut être calculée comme suit$x(t_i)−x(t_{i−1})$ : Ainsi, l'aire du$i^\text{th}$ rectangle est donnée par

\[A_i=y(x(\bar{t_i}))(x(t_i)−x(t_{i−1})). \nonumber \]

Ensuite, une somme riemannienne pour la région est

\[A_n=\sum_{i=1}^ny(x(\bar{t_i}))(x(t_i)−x(t_{i−1})).\nonumber \]

Multiplier et diviser chaque zone par$t_i−t_{i−1}$ donne

\[ \begin{align*} A_n &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{t_i−t_{i−1}}\right)(t_i−t_{i−1}) \\[4pt] &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{Δt}\right)Δt. \end{align*} \nonumber \]

Prendre les limites à mesure que l'infini se$n$ rapproche

\[A=\lim_{n→∞}A_n=∫^b_ay(t)x′(t)\,dt. \nonumber \]

Cela conduit au théorème suivant.

Surface sous une courbe paramétrique

Considérez la courbe plane qui ne se croise pas automatiquement définie par les équations paramétriques

\[x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b \nonumber \]

et supposons que$x(t)$ c'est différenciable. L'aire sous cette courbe est donnée par

\[A=∫^b_ay(t)x′(t)\,dt.\label{ParaArea} \]

Exemple$\PageIndex{4}$: Finding the Area under a Parametric Curve

Trouvez l'aire sous la courbe de la cycloïde définie par les équations

\[x(t)=t−\sin t, \quad y(t)=1−\cos t, \quad \text{for }0≤t≤2π. \nonumber \]

Solution

En utilisant l'équation \ ref {paraArea}, nous avons

\ [\ begin {align*} A &=^b_ay (t) x′ (t) \, dt \ \ [4 points]
&=^ {2π} _0 (1− \ cos t) (1− \ cos t) \, dt \ \ [4 points]
&=^ {2π} _0 (1−2 \ cos t+ \ cos^2t) \, dt \ [4 points]
&=^^ {2π} _0 \ left (1−2 \ cos t+ \ dfrac {1+ \ cos (2t)} {2} \ droite) \, dt \ \ [4 points]
&=^ {2π} _0 \ left (\ dfrac {3} {2} −2} −2 \ cos t+ \ dfrac {\ cos (2t)} {2} \ right) \, dt \ \ [4 points]
&= \ dfrac {3t} {2} −2 \ sin t+ \ dfrac {\ sin (2t)} {4} ^ {2π} _0 \ \ [4 points]
&=3π \ end {align*} \]

Exercice$\PageIndex{4}$

Trouvez l'aire sous la courbe de l'hypocycloïde définie par les équations

\[x(t)=3\cos t+\cos(3t), \quad y(t)=3\sin t−\sin(3t), \quad \text{for }0≤t≤π. \nonumber \]

Allusion: Utilisez l'équation \ ref {paraArea}, ainsi que les identités$\sin α\sin β=\dfrac{1}{2}[\cos(α−β)−\cos(α+β)]$ et$\sin^2t=\dfrac{1−\cos (2t)}{2}$.

Réponse: $A=3π$(Notez que la formule intégrale donne en fait une réponse négative. Cela est dû au fait qu'il$x(t)$ s'agit d'une fonction décroissante sur l'intervalle, c'$[0,π];$est-à-dire que la courbe est tracée de droite à gauche.)

Longueur d'arc d'une courbe paramétrique

En plus de trouver l'aire sous une courbe paramétrique, nous avons parfois besoin de déterminer la longueur de l'arc d'une courbe paramétrique. Dans le cas d'un segment de ligne, la longueur de l'arc est identique à la distance entre les extrémités. Si une particule se déplace d'un point$A$ à un autre$B$ le long d'une courbe, la distance parcourue par cette particule correspond à la longueur de l'arc. Pour développer une formule pour la longueur de l'arc, nous commençons par une approximation par segments de ligne, comme indiqué dans le graphique suivant.

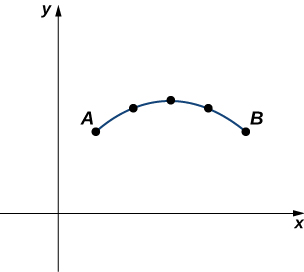
Une ligne courbe dans le premier quadrant avec des points marqués pour x = 1, 2, 3, 4 et 5. Ces points ont des valeurs d'environ 2,1, 2,7, 3, 2,7 et 2,1, respectivement. Les points pour x = 1 et 5 sont marqués A et B, respectivement. — Figure$\PageIndex{7}$ : Approximation d'une courbe par segments de droite.

À partir d'une courbe plane définie par les fonctions$x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b$, nous commençons par partitionner l'intervalle$[a,b]$ en sous-intervalles$n$ égaux :$t_0=a<t_1<t_2<⋯<t_n=b$. La largeur de chaque sous-intervalle est donnée par$Δt=(b−a)/n$. Nous pouvons calculer la longueur de chaque segment de ligne :

\[d_1=\sqrt{(x(t_1)−x(t_0))^2+(y(t_1)−y(t_0))^2} \nonumber \]

\[d_2=\sqrt{(x(t_2)−x(t_1))^2+(y(t_2)−y(t_1))^2} \nonumber \]

etc.

Ensuite, additionnez-les. Nous$s$ indiquons la longueur exacte de l'arc et$s_n$ indiquons l'approximation par segments$n$ de ligne :

\[s≈\sum_{k=1}^ns_k=\sum_{k=1}^n\sqrt{(x(t_k)−x(t_{k−1}))^2+(y(t_k)−y(t_{k−1}))^2}. \label{arc5} \]

Si nous supposons que$x(t)$ et$y(t)$ sont des fonctions dérivables de$t$, alors le théorème de la valeur moyenne s'applique, donc dans chaque sous-intervalle$[t_{k−1},t_k]$ il existe$\hat{t_k}$ et$\tilde{t_k}$ tel que

\[x(t_k)−x(t_{k−1})=x′(\hat{t_k})(t_k−t_{k−1})=x′(\hat{t_k})\,Δt \nonumber \]

\[y(t_k)−y(t_{k−1})=y′(\tilde{t_k})(t_k−t_{k−1})=y′(\tilde{t_k})\,Δt. \nonumber \]

Par conséquent, l'équation \ ref {arc5} devient

\ [\ begin {align*} s ≈ \ sum_ {k=1} ^ns_k &= \ sum_ {k=1} ^n \ sqrt {(x′ (\ hat {t_k}) Δt) ^2+ (y′ (\ tilde {t_k}) Δt) ^2} \ \ [4 points]
&= \ sum_ {k=1} ^n \ sqrt {(x′ (\ hat {t_k})) ^2 (Δt) ^2+ (y′ (\ tilde {t_k})) ^2 (Δt) ^2} \ \ [4 points]
&= \ sum_ {k=1} ^n \ sqrt {(x′ (\ hat {t_k})) ^2+ (y′ (\ tilde {t_k})) ^2} Δt. \ end {align*} \]

Il s'agit d'une somme de Riemann qui correspond approximativement à la longueur de l'arc sur une partition de l'intervalle$[a,b]$. Si nous supposons en outre que les dérivées sont continues et que le nombre de points de la partition augmente sans limite, l'approximation se rapproche de la longueur exacte de l'arc. Cela donne

\ [\ begin {align*} s &= \ lim_ {n→∞} \ sum_ {k=1} ^ns_k \ \ [4 points]
&= \ lim_ {n→∞} \ sum_ {k=1} ^n \ sqrt {(x′ (\ hat {t_k})) ^2+ (y′ (\ tilde {t_k}) ^2} Δt \ [4 points]
&=^b_a \ sqrt {(x′ (t)) ^2+ (y′ (t)) ^2} \, dt. \ end {align*} \]

Lorsque vous prenez la limite, les valeurs de$\hat{t_k}$ et$\tilde{t_k}$ sont toutes deux contenues dans le même intervalle de largeur qui ne cesse de diminuer$Δt$, de sorte qu'elles doivent converger vers la même valeur.

Nous pouvons résumer cette méthode dans le théorème suivant.

Longueur d'arc d'une courbe paramétrique

Considérez la courbe plane définie par les équations paramétriques

\[x=x(t), \quad y=y(t), \quad \text{for }t_1≤t≤t_2 \nonumber \]

et supposons que$x(t)$ et$y(t)$ sont des fonctions différenciables de$t$. Ensuite, la longueur de l'arc de cette courbe est donnée par

\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \label{arcP} \]

À ce stade, une dérivation latérale conduit à une formule précédente pour la longueur de l'arc. Supposons en particulier que le paramètre puisse être éliminé, menant à une fonction$y=F(x)$. Ensuite,$y(t)=F(x(t))$ et la règle de la chaîne donne

\[y′(t)=F′\big(x(t)\big)x′(t). \nonumber \]

En le remplaçant dans l'équation \ ref {ArcP}, on obtient

\ [\ begin {align*} s &=^^ {t_2} _ {t_1} \ sqrt {\ left (\ dfrac {dx} {dt} \ right) ^2+ \ left (F′ (x) \ dfrac {dx} {dt} \ right) ^2} \, dt \ \ [4 points]
&=^ {t_2} _ {t_1} \ sqrt {\ left (\ dfrac {dx} {dt} \ right) ^2 (1+ \ left (F′ (x) \ right) ^2)} \, dt \ \ [4pt]
&=^^ {t_2} _ {t_1} x′ (t) \ sqrt {1+ \ left (\ dfrac {dy} {dx} \ right) ^2} \, dt. \ end {align*} \]

C'est ce que nous avons supposé ici$x′(t)>0$, ce qui est une hypothèse raisonnable. La règle de la chaîne donne$dx=x′(t)\,dt,$ et laisse$a=x(t_1)$ et$b=x(t_2)$ nous obtenons la formule

\[s=∫^b_a\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}\,dx, \nonumber \]

qui est la formule de la longueur d'arc obtenue dans l'Introduction aux applications de l'intégration.

Exemple$\PageIndex{5}$: Finding the Arc Length of a Parametric Curve

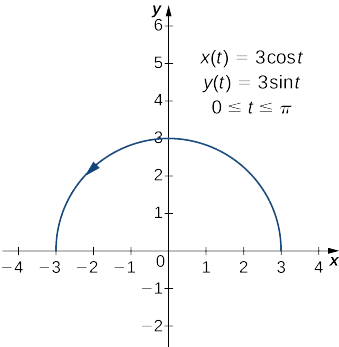
Détermine la longueur de l'arc du demi-cercle définie par les équations

\[x(t)=3\cos t, \quad y(t)=3\sin t, \quad \text{for }0≤t≤π. \nonumber \]

Solution

Les valeurs$t=0$ pour$t=π$ tracer la courbe bleue dans la figure$\PageIndex{8}$. Pour déterminer sa longueur, utilisez l'équation \ ref {ArcP} :

\ [\ begin {align*} s &= \ int^ {t_2} _ {t_1} \ sqrt {\ left (\ dfrac {dx} {dt} \ right) ^2+ \ left (\ dfrac {dy} {dt} \ right) ^2} \, dt \ \ [4pt]
&=hide^π_0 \ sqrt {(−3 \ sin t) ^2+ 3 \ cos t) ^2} \, dt \ \ [4 points]
&=^π_0 \ sqrt {9 \ sin^2t+9 \ cos^2t} \, dt \ \ [4 points]
&=réf \ ^π_0 \ sqrt {9 (\ sin^2t+ \ cos^2t)} \, dt \ \ [4 points]
&=^π_03 \, dt=3t \ big|^π_0 \ \ [4 points]
&=3π \ text {unités}. \ end {align*} \]

Notez que la formule pour la longueur de l'arc d'un demi-cercle est$πr$ et que le rayon de ce cercle est$3$. C'est un excellent exemple d'utilisation du calcul pour dériver une formule connue d'une quantité géométrique.

Un demi-cercle de rayon 3 est dessiné. Il y a une flèche pointant dans le sens antihoraire. Trois équations sont également écrites sur le graphique : x (t) = 3 cos (t), y (t) = 3 sin (t) et 0 ≤ t ≤ π. — Figure$\PageIndex{8}$ : La longueur de l'arc du demi-cercle est égale à son rayon multiplié par$π$.

Exercice$\PageIndex{5}$

Détermine la longueur de l'arc de la courbe définie par les équations

\[x(t)=3t^2, \quad y(t)=2t^3, \quad \text{for }1≤t≤3. \nonumber \]

Allusion: Utilisez l'équation \ ref {ArcP}.

Réponse: $s=2(10^{3/2}−2^{3/2})≈57.589$unités

Nous revenons maintenant au problème posé au début de la section concernant une balle de baseball quittant la main d'un lanceur. Ignorer l'effet de la résistance à l'air (sauf s'il s'agit d'une boule courbe !) , la balle suit une trajectoire parabolique. En supposant que la main du lanceur se trouve à l'origine et que la balle se déplace de gauche à droite dans la direction de l'$x$axe positif, les équations paramétriques de cette courbe peuvent être écrites comme

\[x(t)=140t, \quad y(t)=−16t^2+2t \nonumber \]

où$t$ représente le temps. Nous calculons d'abord la distance parcourue par la balle en fonction du temps. Cette distance est représentée par la longueur de l'arc. Nous pouvons modifier légèrement la formule de la longueur de l'arc. Réécrivez d'abord les fonctions$x(t)$ et$y(t)$ utilisez v comme variable indépendante, afin d'éliminer toute confusion avec le paramètre$t$ :

\[x(v)=140v, \quad y(v)=−16v^2+2v. \nonumber \]

Ensuite, nous écrivons la formule de la longueur de l'arc comme suit :

\ [\ begin {align*} s (t) &=^t_0 \ sqrt {(\ dfrac {dx} {dv}) ^2+ (\ dfrac {dy} {dv}) ^2} \, dv \ \ [4 points]
&=hour^t_0 \ sqrt {140^2+ (−32v+2) ^2} \, dv \ end {align*} \]

La variable$v$ agit comme une variable fictive qui disparaît après intégration, laissant la longueur de l'arc en fonction du temps$t$. Pour intégrer cette expression, nous pouvons utiliser une formule de l'annexe A,

\[∫\sqrt{a^2+u^2}\,du=\dfrac{u}{2}\sqrt{a^2+u^2}+\dfrac{a^2}{2}\ln ∣u+\sqrt{a^2+u^2}∣+C. \nonumber \]

Nous fixons$a=140$ et$u=−32v+2.$ cela donne$du=−32\,dv,$$dv=−\dfrac{1}{32}\,du.$ donc

\ [\ begin {align*} ∫ \ sqrt {140^2+ (−32v+2) ^2} \, dv &=− \ dfrac {1} {32} ∫ \ sqrt {a^2+u^2} \, du \ \ [4 points]
&=− \ dfrac {1} {32} \ left [\ dfrac {(−32v+2)} {2} \ sqrt {140^2+ (−32v+2) ^2} + \ dfrac {140^2} {2} \ ln (−32 v+2) + \ sqrt {140^2+ (−32 v+2) ^2} |+C \ right] \ end {align*} \]

\ [\ begin {align*} s (t) &=- \ dfrac {1} {32} \ left [\ dfrac {(-32t+2)} {2} \ sqrt {140^2+ (-32t+2) ^2} + \ dfrac {140^2} {2} \ ln \ left | (-32t+2) + \ sqrt {140^2+ (-32t+2) + \ sqrt {140^2} (-32t+2) +2) ^2} \ right | \ right] + \ dfrac {1} {32} \ left [\ sqrt {140^2+2^2} + \ dfrac {140^2} {2} \ ln \ left |2+ \ sqrt {140^2+2^2} \ right | \ right] \ \ [4pt]
&= \ left (\ dfrac {t} {2} - \ dfrac {1} {32} \ droite) \ sqrt {1024t^2-128t+19604} - \ dfrac {1225} {4} \ ln \ left | (-32t+2) + \ sqrt {1024t^2-128t+19604} \ right |+ \ dfrac {\ sqrt {19604}} {32} + \ dfrac {1225} {4} \ ln (2+ \ sqrt {19604}) \ end {align*}. \ aucun numéro \]

Cette fonction représente la distance parcourue par la balle en fonction du temps. Pour calculer la vitesse, prenez la dérivée de cette fonction par rapport à$t$. Bien que cela puisse sembler une tâche ardue, il est possible d'obtenir la réponse directement à partir du théorème fondamental du calcul :

\[\dfrac{d}{dx}∫^x_af(u)\,du=f(x). \nonumber \]

Donc

\ [\ begin {align*} s′ (t) &= \ dfrac {d} {dt} \ Big [s (t) \ Big] \ \ [4 points]
&= \ dfrac {d} {dt} \ left [^^t_0 \ sqrt {140^2+ (−32v+2) ^2} \, dv \ right] \ \ [4 points]
&= \ {sqrt 140^2+ (−32t+2) ^2} \ \ [4 points]
&= \ sqrt {1024t^2−128t+19604} \ \ [4 points]
&=2 \ sqrt {256t^2−32t+4901}. \ end {align*} \ nonumber \]

Un tiers de seconde après que le ballon quitte la main du lanceur, la distance parcourue est égale à

\ [\ begin {align*} s \ left (\ frac {1} {3} \ right) &= \ left (\ frac {1/3} {2} − \ frac {1} {32} \ right) \ sqrt {1024 \ left (\ frac {1} {3} \ right) ^2−128 \ left (\ frac {1} {3} \ right) +19604} \ right \
&− \ frac {1225} {4} \ ln \ Bigg| \ left (−32 \ left (\ frac {1} {3} \ right) +2 \ right) + \ sqrt {1024 \ left (\ frac {1} {3} \ right) ^2−128 \ left (\ frac {1} {3} \ right) +19604} \ Bigg| \ \
&+ \ frac {\ sqrt {19604}} {32} + \ frac {1225} {4} \ ln (2+ \ sqrt {19604}) \ \ [4 points]
&≈ 46,69 \ text {pieds}. \ end {align*} \]

Cette valeur représente un peu plus des trois quarts du trajet jusqu'à la plaque d'origine. La vitesse de la balle est

$s′\left(\frac{1}{3}\right)=2\sqrt{256\left(\frac{1}{3}\right)^2−32\left(\frac{1}{3}\right)+4901}≈140.27$pieds/s.

Cette vitesse se traduit par environ$95$ mi/h, une balle rapide dans les ligues majeures.

Surface générée par une courbe paramétrique

Rappelons le problème de la détermination de la surface d'un volume de révolution. Dans Curve Length and Surface Area, nous avons dérivé une formule pour déterminer la surface d'un volume généré par une fonction$y=f(x)$ allant de$x=a$ à$x=b,$ tournant autour de l'$x$axe :

\[S=2π∫^b_af(x)\sqrt{1+(f′(x))^2}\,dx. \nonumber \]

Nous considérons maintenant un volume de révolution généré en faisant tourner une courbe définie de manière paramétrique$x=x(t), \quad y=y(t), \quad \text{for }a≤t≤b$ autour de l'$x$axe, comme indiqué sur la figure$\PageIndex{9}$.

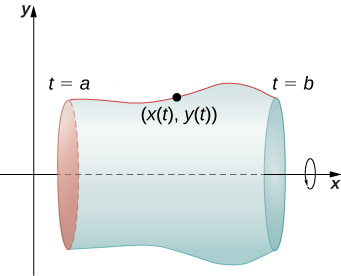
Une courbe est dessinée dans le premier quadrant avec les extrémités marquées t = a et t = b. Sur cette courbe se trouve un point marqué (x (t), y (t)). Un cercle avec une flèche dessiné autour de l'axe x semble indiquer une rotation autour de l'axe x, et une forme qui accompagne cette courbe semble être celle que vous obtiendriez si vous faisiez pivoter la courbe autour de l'axe X. — Figure$\PageIndex{9}$ : Surface de révolution générée par une courbe définie de manière paramétrique.

La formule analogue pour une courbe définie de manière paramétrique est

\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \label{ParSurface} \]

à condition que ce ne$y(t)$ soit pas négatif sur$[a,b]$.

Exemple$\PageIndex{6}$: Finding Surface Area

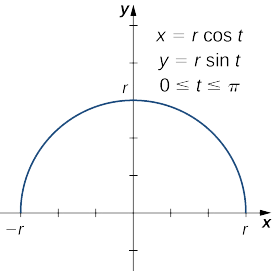
Détermine la surface d'une sphère dont le rayon est$r$ centré sur l'origine.

Solution

Nous commençons par la courbe définie par les équations

\[x(t)=r\cos t, \quad y(t)=r\sin t, \quad \text{for }0≤t≤π. \nonumber \]

Cela génère un demi-cercle supérieur de rayon$r$ centré sur l'origine, comme indiqué dans le graphique suivant.

Un demi-cercle est dessiné avec un rayon r. Trois équations sont également écrites sur le graphique : x (t) = r cos (t), y (t) = r sin (t) et 0 ≤ t ≤ π. — Figure$\PageIndex{10}$ : Un demi-cercle généré par des équations paramétriques.

Lorsque cette courbe tourne autour de l'$x$axe -, elle génère une sphère de rayon$r$. Pour calculer la surface de la sphère, nous utilisons l'équation \ ref {parSurface} :

\ [\ begin {align*} S &= 2ππ^b_ay (t) \ sqrt {(x′ (t)) ^2+ (y′ (t)) ^2} \, dt \ \ [4 points]
&=2π^π_0r \ sin t \ sqrt {(−r \ sin t) ^2+ (r \ cos t) ^2} \, dt \ \ [4 pt]
&=2π^π_0r \ sin t \ sqrt {r^2 \ sin^2t+r^2 \ cos^2t} \, dt \ \ [4 points]
&=2ππ^π_0r \ sin t \ sqrt {r^2 (\ sin^2t+ \ cos^2t)} \, dt \ \ [4 points]
&=2πr^π_0r^2 \ sin t \, dt \ \ [4 points]
&=2πr^2 \ left (− \ cos t \ big|^π_0 \ droite) \ \ [4 points]
&=2πr^2 (− \ cos π+ \ cos 0) \ \ [4 points]
&=4πr^2 \ text {unités} ^2. \ end {align*} \ nonumber \]

Il s'agit en fait de la formule de la surface d'une sphère.

Exercice$\PageIndex{6}$

Trouve la surface générée lorsque la courbe plane définie par les équations

\[x(t)=t^3, \quad y(t)=t^2, \quad \text{for }0≤t≤1 \nonumber \]

tourne autour de l'$x$axe.

Allusion: Utilisez l'équation \ ref {parSurface}. Lors de l'évaluation de l'intégrale, utilisez une$u$ substitution.

Réponse: $A=\dfrac{π(494\sqrt{13}+128)}{1215} \text{ units}^2$

Concepts clés

La dérivée de la courbe$x=x(t)$ définie de manière paramétrique$y=y(t)$ peut être calculée à l'aide de la formule$\dfrac{dy}{dx}=\dfrac{y′(t)}{x′(t)}$. À l'aide de la dérivée, nous pouvons trouver l'équation d'une droite tangente à une courbe paramétrique.
L'aire entre une courbe paramétrique et l'$x$axe -peut être déterminée à l'aide de la formule$\displaystyle A=∫^{t_2}_{t_1}y(t)x′(t)\,dt.$
La longueur de l'arc d'une courbe paramétrique peut être calculée à l'aide de la formule\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \nonumber \]
La surface d'un volume de révolution tournant autour de l'$x$axe -est donnée par\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]
Si la courbe tourne autour de l'$y$axe -, la formule est\[S=2π∫^b_a x(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]

Équations clés

Dérivée d'équations paramétriques

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)} \nonumber \]

Dérivée du second ordre des équations paramétriques

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)=\dfrac{(d/dt)(dy/dx)}{dx/dt} \nonumber \]

Surface sous une courbe paramétrique

\[A=∫^b_ay(t)x′(t)\,dt \nonumber \]

Longueur d'arc d'une courbe paramétrique

\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \nonumber \]

Surface générée par une courbe paramétrique

\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \nonumber \]

Dérivée des équations paramétriques

Une preuve

Exemple\(\PageIndex{1}\): Finding the Derivative of a Parametric Curve

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Finding a Tangent Line

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Finding a Second Derivative

Exercice\(\PageIndex{3}\)

Surface sous une courbe paramétrique

Exemple\(\PageIndex{4}\): Finding the Area under a Parametric Curve

Exercice\(\PageIndex{4}\)

Longueur d'arc d'une courbe paramétrique

Exemple\(\PageIndex{5}\): Finding the Arc Length of a Parametric Curve

Exercice\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\): Finding Surface Area

Exercice\(\PageIndex{6}\)