11.1E : Exercices pour la section 11.1

Last updated
Save as PDF

Page ID: 197306

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, esquissez les courbes ci-dessous en éliminant le paramètre$t$. Donnez l'orientation de la courbe.

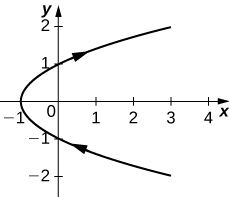
1)$ x=t^2+2t, \quad y=t+1$

Réponse

Orientation : de bas en haut

$Une parabole ouverte vers la droite, (−1, 0) étant le point le plus à gauche, la flèche allant du bas vers le haut en passant par (−1, 0).$

2)$ x=\cos(t), \quad y=\sin(t), \quad \text{for } (0,2π]$

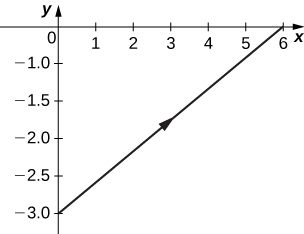
3)$ x=2t+4, \quad y=t−1$

Réponse

Orientation : de gauche à droite

$Une ligne droite passant par (0, −3) et (6, 0) avec une flèche pointant vers le haut et vers la droite.$

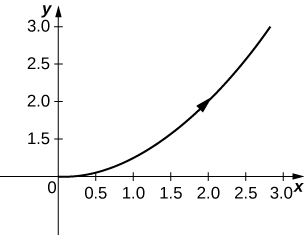
4)$ x=3−t, \quad y=2t−3, \quad \text{for }1.5≤t≤3$

Dans l'exercice 5, éliminez le paramètre et esquissez le graphique.

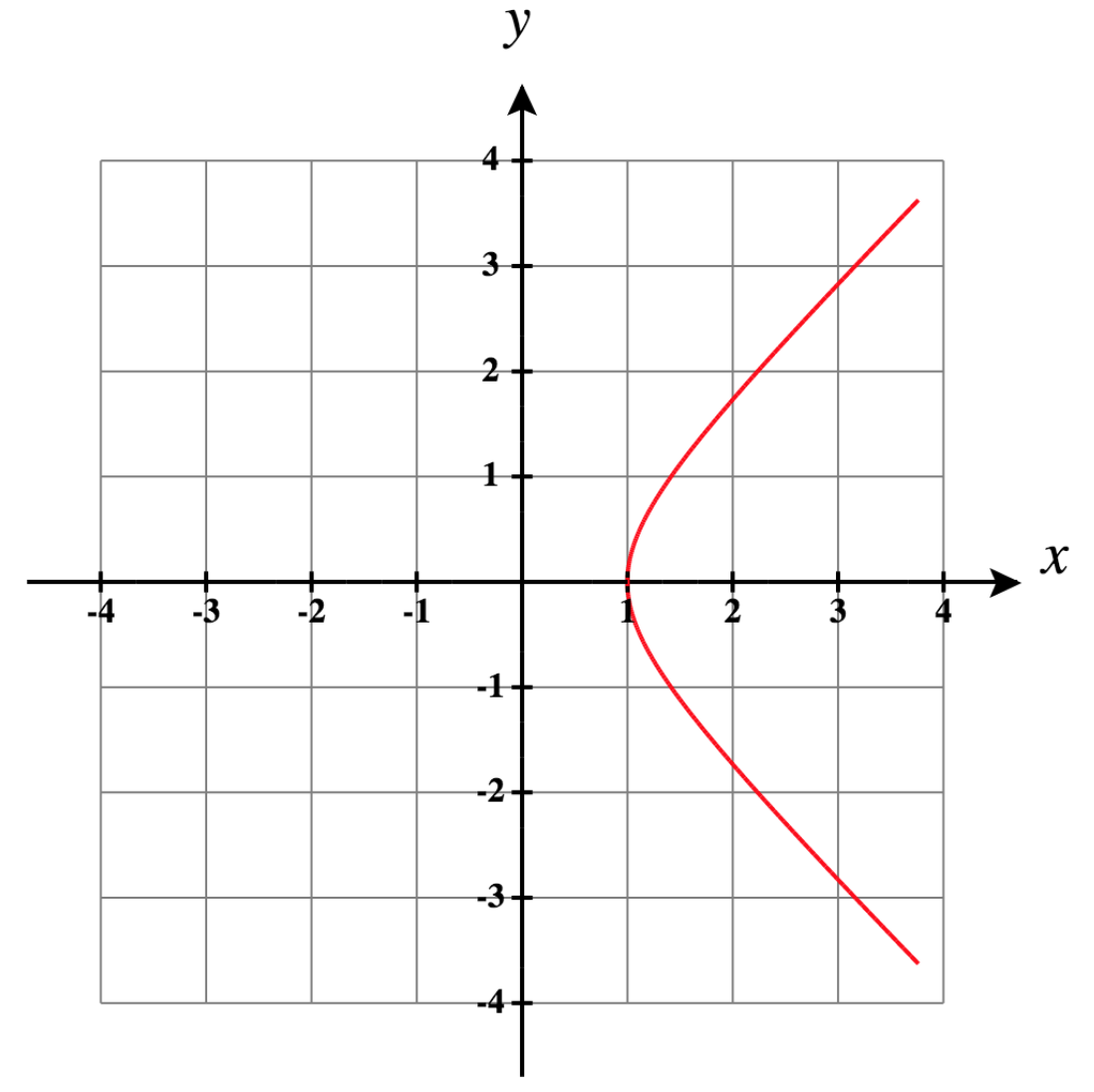
5)$x=2t^2,\quad y=t^4+1$

Réponse

$ y=\dfrac{x^2}{4}+1$

$Une demi-parabole partant de l'origine et passant par (2, 2), la flèche pointée vers le haut et vers la droite.$

Dans les exercices 6 à 9, utilisez la technologie (CAS ou calculatrice) pour esquisser les équations paramétriques.

6) [T]$x=t^2+t, \quad y=t^2−1$

7) [T]$ x=e^{−t}, \quad y=e^{2t}−1$

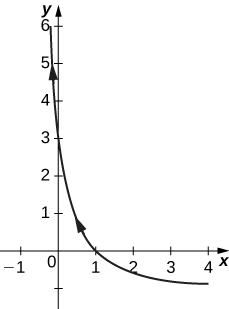
Réponse: $Une courbe passant par (1, 0) et (0, 3) avec une flèche pointant vers le haut et vers la gauche.$

8) [T]$ x=3\cos t, \quad y=4\sin t$

9) [T]$ x=\sec t, \quad y=\cos t$

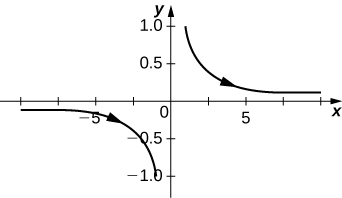
Réponse: $Un graphique avec des asymptotes sur les axes x et y. Une partie du graphique se trouve dans le troisième quadrant, la flèche pointant vers le bas et vers la droite. Une partie du graphique se trouve dans le premier quadrant, la flèche pointant vers le bas et vers la droite.$

Dans les exercices 10 à 20, esquissez les équations paramétriques en éliminant le paramètre. Indiquez toute asymptote du graphique.

10)$ x=e^t, \quad y=e^{2t}+1$

11)$ x=6\sin(2θ), \quad y=-4\cos(2θ)$

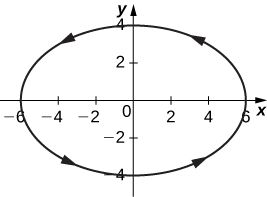
Réponse: $Ellipse d'axe mineur vertical et de longueur 8 et grand axe horizontal et de longueur 12 centrée à l'origine. Les flèches vont dans le sens antihoraire.$

(12)$ x=\cos θ, \quad y=2\sin(2θ)$

(13)$ x=3−2\cos θ, \quad y=−5+3\sin θ$

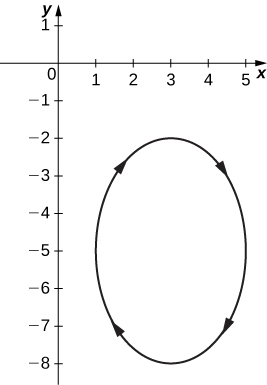
Réponse: $Une ellipse dans le quatrième quadrant avec un petit axe horizontal et de longueur 4 et un grand axe vertical et de longueur 6. Les flèches s'orientent dans le sens des aiguilles$

(14)$ x=4+2\cos θ, \quad y=−1+\sin θ$

(15)$ x=\sec t, \quad y=\tan t$

Réponse

Les asymptotes sont$ y=x$ et$ y=−x$

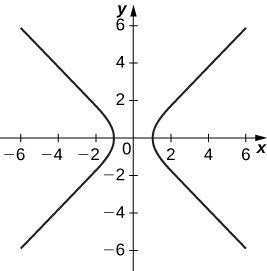
$Un graphe avec des asymptotes à y = x et y = −x. La première partie du graphe apparaît dans les deuxième et troisième quadrants avec le sommet à (−1, 0). La deuxième partie du graphe se trouve dans les premier et quatrième quadrants avec le sommet comme (1, 0).$

16)$ x=\ln(2t), \quad y=t^2$

17)$ x=e^t, \quad y=e^{2t}$

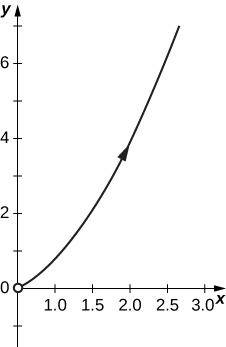
Réponse: $Courbe commençant légèrement au-dessus de l'origine et augmentant vers la droite, la flèche pointant vers le haut et vers la droite.$

18)$ x=e^{−2t}, \quad y=e^{3t}$

19)$ x=t^3, \quad y=3\ln t$

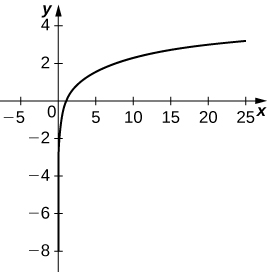
Réponse: $Une courbe dont l'asymptote est l'axe y. La courbe commence dans le quatrième quadrant et augmente rapidement jusqu'à (1, 0), point auquel elle augmente beaucoup plus lentement.$

(20)$ x=4\sec θ, \quad y=3\tan θ$

Dans les exercices 21 à 38, convertissez les équations paramétriques d'une courbe en forme rectangulaire. Aucun croquis n'est nécessaire. Indiquez le domaine de la forme rectangulaire.

(21)$ x=t^2−1, \quad y=\dfrac{t}{2}$

Réponse: $ x=4y^2−1;$domaine :$ x∈[1,∞)$.

(22)$ x=\dfrac{1}{\sqrt{t+1}}, \quad y=\dfrac{t}{1+t}, \quad \text{for }t>−1$

23)$ x=4\cos θ, \quad y=3\sin θ, \quad \text{for }t∈(0,2π]$

Réponse: $ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1;$domaine$ x∈[−4,4].$

(24)$ x=\cosh t, \quad y=\sinh t$

25)$ x=2t−3, \quad y=6t−7$

Réponse: $ y=3x+2;$domaine : tous les nombres réels.

(26)$ x=t^2, \quad y=t^3$

(27)$ x=1+\cos t, \quad y=3−\sin t$

Réponse: $ (x−1)^2+(y−3)^2=1$; domaine :$ x∈[0,2]$.

(28)$ x=\sqrt{t}, \quad y=2t+4$

(29)$ x=\sec t, \quad y=\tan t, \quad \text{for } π≤t<\frac{3π}{2}$

Réponse: $ y=\sqrt{x^2−1}$; domaine :$ x∈(−\infty,-1]$.

(30)$ x=2\cosh t, \quad y=4\sinh t$

31)$ x=\cos(2t), \quad y=\sin t$

Réponse: $ y^2=\dfrac{1−x}{2};$domaine :$ x∈[-1,1].$

32)$ x=4t+3, \quad y=16t^2−9$

33)$ x=t^2, \quad y=2\ln t, \quad \text{for }t≥1$

Réponse: $ y=\ln x;$domaine :$ x∈[1,∞).$

34)$ x=t^3, \quad y=3\ln t, \quad \text{for }t≥1$

35)$ x=t^n, \quad y=n\ln t, \quad \text{for } t≥1,$ où$n$ est un entier naturel

Réponse: $ y=\ln x;$domaine :$ x∈(0,∞).$

36)$ x=\ln(5t), \quad y=\ln(t^2)$ où$ 1≤t≤e$

(37)$ x=2\sin(8t), \quad y=2\cos(8t)$

Réponse: $ x^2+y^2=4;$domaine :$ x∈[−2,2].$

38)$ x=\tan t, \quad y=\sec^2t−1$

Dans les exercices 39 à 48, les paires d'équations paramétriques représentent des lignes, des paraboles, des cercles, des ellipses ou des hyperboles. Nommez le type de courbe de base que représente chaque paire d'équations.

39)$ x=3t+4, \quad y=5t−2$

Réponse: ligne

40)$ x−4=5t, \quad y+2=t$

41)$ x=2t+1, \quad y=t^2−3$

Réponse: parabole

(42)$ x=3\cos t, \quad y=3\sin t$

43)$ x=2\cos(3t), \quad y=2\sin(3t)$

Réponse: encercler

44)$ x=\cosh t, \quad y=\sinh t$

45)$ x=3\cos t, \quad y=4\sin t$

Réponse: ellipse

46)$ x=2\cos(3t), \quad y=5\sin(3t)$

47)$ x=3\cosh(4t) \quad y=4\sinh(4t)$

Réponse: la branche droite d'une hyperbole à ouverture horizontale

48)$ x=2\cosh t, \quad y=2\sinh t$

49) Montre qui$ x=h+r\cos θ, \quad y=k+r\sin θ$ représente l'équation d'un cercle.

50) Utilisez les équations du problème précédent pour trouver un ensemble d'équations paramétriques pour un cercle dont le rayon est$5$ et dont le centre est$ (−2,3)$.

Dans les exercices 51 à 53, utilisez un utilitaire graphique pour représenter graphiquement la courbe représentée par les équations paramétriques et identifier la courbe à partir de son équation.

51) [T]$ x=θ+\sin θ, \quad y=1−\cos θ$

Réponse

Les équations représentent une cycloïde.

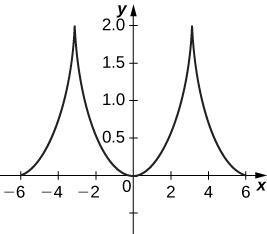
$Un graphique commençant à (−6, 0) augmentant rapidement jusqu'à un point précis à (−3, 2), puis diminuant rapidement jusqu'à l'origine. Le graphique est symétrique par rapport à l'axe y, de sorte qu'il augmente rapidement jusqu'à (3, 2) avant de diminuer rapidement jusqu'à (6, 0).$

52) [T]$ x=2t−2\sin t, \quad y=2−2\cos t$

53) [T]$ x=t−0.5\sin t, \quad y=1−1.5\cos t$

Réponse: $Un graphique commençant approximativement à (−6, 0) augmentant jusqu'à un point arrondi, puis décroissant jusqu'à environ (0, −0,5). Le graphique est symétrique par rapport à l'axe y, de sorte qu'il augmente jusqu'à un point arrondi avant de diminuer approximativement (6, 0).$

54) Un avion qui se déplace horizontalement à 100 m/s au-dessus d'un sol plat à une altitude de 4 000 mètres doit déposer un colis d'urgence sur une cible au sol. La trajectoire du colis est donnée par l'origine du$ x=100t, \quad y=−4.9t^2+4000, \quad \text{where }t≥0$ point au sol situé directement sous l'avion au moment du largage. À combien de mètres horizontaux avant la cible le colis doit-il être libéré pour atteindre la cible ?

55) La trajectoire d'une balle est donnée$ x=v_0(\cos α)t, \quad y=v_0(\sin α)t−\frac{1}{2}gt^2$ par$ v_0=500$ m/s,$g=9.8=9.8\text{ m/s}^2$, et$ α=30$ degrés. Quand la balle touchera-t-elle le sol ? À quelle distance du pistolet la balle touchera-t-elle le sol ?

Réponse: 22 092 mètres à environ 51 secondes.

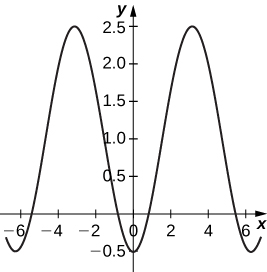
56) [T] Utilisez la technologie pour esquisser la courbe représentée par$ x=\sin(4t), \quad y=\sin(3t), \quad \text{for }0≤t≤2π$.

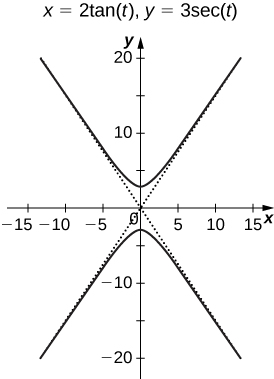
57) [T] Utiliser la technologie pour dessiner$ x=2\tan(t), \quad y=3\sec(t), \quad \text{for }−π<t<π.$

Réponse: $Un graphe dont les asymptotes sont approximativement proches de y = x et y = −x. La première partie du graphe se trouve dans les premier et deuxième quadrants avec un sommet proche de (0, 3). La deuxième partie du graphique se trouve dans les troisième et quatrième quadrants avec un sommet proche de (0, -3).$

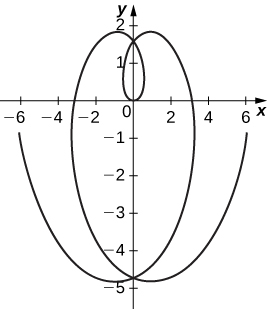
58) Esquissez la courbe connue sous le nom d'épitrochoïde, qui donne la trajectoire d'un point sur un cercle de rayon$b$ lorsqu'il roule à l'extérieur d'un cercle de rayon$a$. Les équations sont

$ x=(a+b)\cos t−c⋅\cos\left[\frac{(a+b)t}{b}\right], \quad y=(a+b)\sin t−c⋅\sin\left[\frac{(a+b)t}{b}\right]$.

Laissez$ a=1,\;b=2,\;c=1.$

59) [T] Utilisez la technologie pour esquisser la courbe en spirale donnée par$ x=t\cos(t), \quad y=t\sin(t)$ pour$ −2π≤t≤2π.$

Réponse: $Un graphique commençant à peu près (−6, −1) diminuant au minimum dans le troisième quadrant proche de (−1, −4,8) augmentant approximativement (0, −4,7) et (3, 0) jusqu'à un maximum près de (1, 1,9) avant de diminuer jusqu'à (0, 1,5) jusqu'à l'origine. Le graphe est symétrique par rapport à l'axe y, de sorte qu'il augmente jusqu'à (0, 1,5) jusqu'à un maximum dans le deuxième quadrant, diminue à nouveau jusqu'à (0, −4,7), puis augmente jusqu'à (6, -1).$

60) [T] Utilisez la technologie pour représenter graphiquement la courbe donnée par les équations paramétriques$ x=2\cot(t), \quad y=1−\cos(2t), \quad \text{for }−π/2≤t≤π/2.$ Cette courbe est connue sous le nom de sorcière d'Agnesi.

61) [T] Esquissez la courbe donnée par des équations paramétriques$ x=\cosh(t), \quad y=\sinh(t),$ pour$ −2≤t≤2.$

Réponse: $Un graphe vaguement parabolique avec un sommet au point (1, 0) qui s'ouvre vers la droite.$