11.1 : Équations paramétriques
- Page ID
- 197297
- Tracez une courbe décrite par des équations paramétriques.
- Convertissez les équations paramétriques d'une courbe dans le formulaire\(y=f(x)\).
- Reconnaissez les équations paramétriques des courbes de base, telles qu'une ligne et un cercle.
- Reconnaissez les équations paramétriques d'une cycloïde.
Dans cette section, nous examinons les équations paramétriques et leurs graphes. Dans le système de coordonnées bidimensionnel, les équations paramétriques sont utiles pour décrire des courbes qui ne sont pas nécessairement des fonctions. Le paramètre est une variable indépendante qui\(y\) dépend à la fois\(x\) des valeurs d'une courbe plane et qui, à mesure que le paramètre augmente,\(y\) trace une trajectoire le long d'une courbe plane.\(x\) Par exemple, si le paramètre est\(t\) (un choix courant), il\(t\) peut représenter le temps. Ensuite,\(x\) et\(y\) sont définis comme des fonctions du temps, et\((x(t),y(t))\) peuvent décrire la position dans le plan d'un objet donné lorsqu'il se déplace le long d'une trajectoire incurvée.
Les équations paramétriques et leurs graphes
Pensez à l'orbite de la Terre autour du Soleil. Notre année dure environ 365,25 jours, mais pour cette discussion, nous utiliserons 365 jours. Le 1er janvier de chaque année, la position physique de la Terre par rapport au Soleil est pratiquement la même, sauf pour les années bissextiles, où le décalage introduit par le\(\frac{1}{4}\) jour supplémentaire de temps d'orbite est intégré au calendrier. Nous appelons le 1er janvier « jour 1 » de l'année. Ensuite, par exemple, le jour 31 correspond au 31 janvier, le jour 59 au 28 février, et ainsi de suite.
Le nombre de jours d'une année peut être considéré comme une variable qui détermine la position de la Terre sur son orbite. Lorsque la Terre tourne autour du Soleil, sa position physique change par rapport au Soleil. Après une année complète, nous sommes revenus là où nous avions commencé et une nouvelle année commence. Selon les lois du mouvement planétaire de Kepler, la forme de l'orbite est elliptique, le Soleil se trouvant à l'un des foyers de l'ellipse. Nous étudions cette idée plus en détail dans Conic Sections.
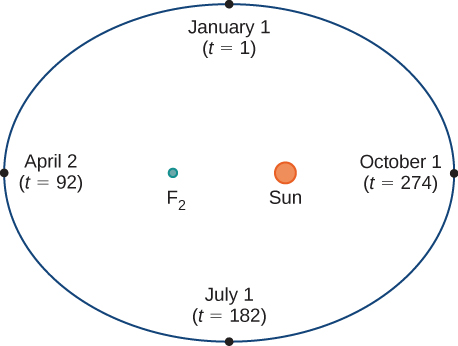
La figure\( \PageIndex{1}\) représente l'orbite de la Terre autour du Soleil pendant un an. Le point marqué\(F_2\) est l'un des foyers de l'ellipse ; l'autre foyer est occupé par le Soleil. Si nous superposons des axes de coordonnées sur ce graphique, nous pouvons attribuer des paires ordonnées à chaque point de l'ellipse (Figure\( \PageIndex{2}\)). Ensuite, chaque\(x\) valeur du graphique est une valeur de position en fonction du temps, et chaque\(y\) valeur est également une valeur de position en fonction du temps. Ainsi, chaque point du graphique correspond à une valeur de la position de la Terre en fonction du temps.
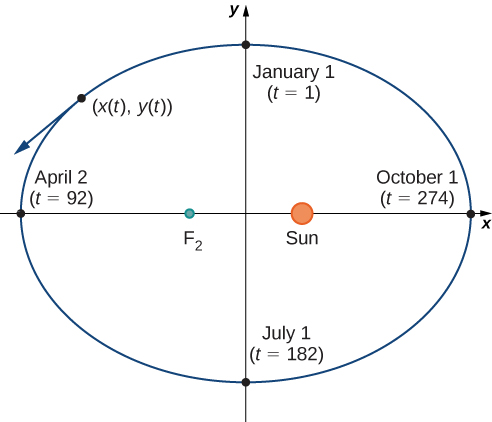
Nous pouvons déterminer les fonctions\(x(t)\) et\(y(t)\), ainsi, paramétrer l'orbite de la Terre autour du Soleil. La variable\(t\) est appelée paramètre indépendant et, dans ce contexte, représente le temps par rapport au début de chaque année.
Une courbe dans le\((x,y)\) plan peut être représentée de manière paramétrique. Les équations utilisées pour définir la courbe sont appelées équations paramétriques.
Si\(x\) et\(y\) sont des fonctions continues de\(t\) sur un intervalle\(I\), alors les équations
\[x=x(t) \nonumber \]
et
\[y=y(t) \nonumber \]
sont appelées équations paramétriques et\(t\) s'appellent le paramètre. L'ensemble des points\((x,y)\) obtenus en\(t\) variant au cours de l'intervalle\(I\) est appelé graphe des équations paramétriques. Le graphe des équations paramétriques est appelé courbe paramétrique ou courbe plane et est désigné par\(C\).
Notez dans cette définition que\(x\) et\(y\) sont utilisés de deux manières. La première est fonction de la variable indépendante\(t\). Comme\(t\) varie au cours de l'intervalle\(I\), les fonctions\(x(t)\) et\(y(t)\) génèrent un ensemble de paires ordonnées\((x,y)\). Cet ensemble de paires ordonnées génère le graphe des équations paramétriques. Dans cette seconde utilisation, pour désigner les paires ordonnées,\(x\) et\(y\) sont des variables. Il est important de distinguer les variables\(x\) et\(y\) les fonctions\(x(t)\) et\(y(t)\).
Esquissez les courbes décrites par les équations paramétriques suivantes :
- \(x(t)=t−1, \quad y(t)=2t+4,\quad \text{for }−3≤t≤2\)
- \(x(t)=t^2−3, \quad y(t)=2t+1,\quad \text{for }−2≤t≤3\)
- \(x(t)=4 \cos t, \quad y(t)=4 \sin t,\quad \text{for }0≤t≤2π\)
Solution
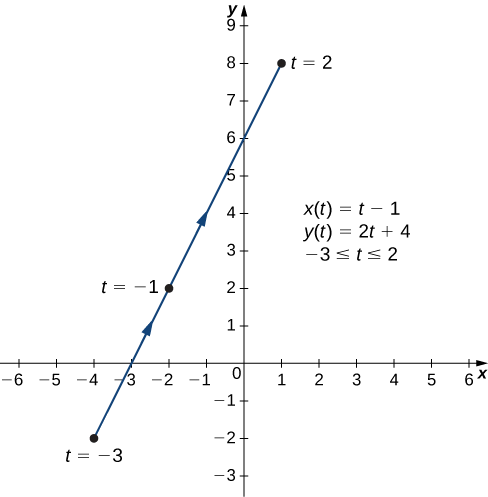
a. Pour créer un graphique de cette courbe, configurez d'abord un tableau de valeurs. Puisque la variable indépendante\(y(t)\) est à la fois\(x(t)\) et\(t\),\(t\) apparaisse dans la première colonne. Puis\(x(t)\) et\(y(t)\) apparaîtra dans les deuxième et troisième colonnes du tableau.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >−3 | \ (x (t) \) » style="vertical-align:middle ; « >−4 | \ (y (t) \) » style="vertical-align:middle ; « >−2 |
| \ (t \) » style="vertical-align:middle ; « >−2 | \ (x (t) \) » style="vertical-align:middle ; « >−3 | \ (y (t) \) » style="vertical-align:middle ; « >0 |
| \ (t \) » style="vertical-align:middle ; « >−1 | \ (x (t) \) » style="vertical-align:middle ; « >−2 | \ (y (t) \) » style="vertical-align:middle ; ">2 |
| \ (t \) » style="vertical-align:middle ; « >0 | \ (x (t) \) » style="vertical-align:middle ; « >−1 | \ (y (t) \) » style="vertical-align:middle ; « >4 |
| \ (t \) » style="vertical-align:middle ; « >1 | \ (x (t) \) » style="vertical-align:middle ; « >0 | \ (y (t) \) » style="vertical-align:middle ; « >6 |
| \ (t \) » style="vertical-align:middle ; « >2 | \ (x (t) \) » style="vertical-align:middle ; « >1 | \ (y (t) \) » style="vertical-align:middle ; « >8 |
Les deuxième et troisième colonnes de ce tableau fournissent un ensemble de points à tracer. Le graphique de ces points apparaît sur la figure\( \PageIndex{3}\). Les flèches sur le graphique indiquent l'orientation du graphe, c'est-à-dire la direction dans laquelle se déplace un point sur le graphique lorsque t varie de -3 à 2.
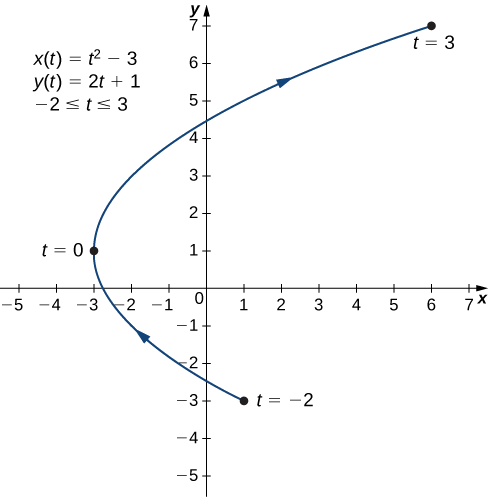
b. Pour créer un graphique de cette courbe, configurez à nouveau un tableau de valeurs.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >−2 | \ (x (t) \) » style="vertical-align:middle ; « >1 | \ (y (t) \) » style="vertical-align:middle ; « >−3 |
| \ (t \) » style="vertical-align:middle ; « >−1 | \ (x (t) \) » style="vertical-align:middle ; « >−2 | \ (y (t) \) » style="vertical-align:middle ; « >−1 |
| \ (t \) » style="vertical-align:middle ; « >0 | \ (x (t) \) » style="vertical-align:middle ; « >−3 | \ (y (t) \) » style="vertical-align:middle ; ">1 |
| \ (t \) » style="vertical-align:middle ; « >1 | \ (x (t) \) » style="vertical-align:middle ; « >−2 | \ (y (t) \) » style="vertical-align:middle ; « >3 |
| \ (t \) » style="vertical-align:middle ; « >2 | \ (x (t) \) » style="vertical-align:middle ; « >1 | \ (y (t) \) » style="vertical-align:middle ; « >5 |
| \ (t \) » style="vertical-align:middle ; « >3 | \ (x (t) \) » style="vertical-align:middle ; « >6 | \ (y (t) \) » style="vertical-align:middle ; « >7 |
Les deuxième et troisième colonnes de ce tableau indiquent un ensemble de points à tracer (Figure\( \PageIndex{4}\)). Le premier point du graphique (correspondant à\(t=−2\)) possède des coordonnées\((1,−3)\) et le dernier point (correspondant à\(t=3\)) possède des coordonnées\((6,7)\). Au fur et à mesure que l'on\(t\) progresse de\(−2\) à\(3\), le point de la courbe se déplace le long d'une parabole. La direction dans laquelle se déplace le point est à nouveau appelée orientation et est indiquée sur le graphique.
c. Dans ce cas, utilisez des multiples de\(π/6\) for\(t\) et créez une autre table de valeurs :
| \(t\) | \(x(t)\) | \(y(t)\) | \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >0 | \ (x (t) \) » style="vertical-align:middle ; « >4 | \ (y (t) \) » style="vertical-align:middle ; « >0 | \ (t \) » style="vertical-align:middle ; « >\(\frac{7π}{6}\) | \ (x (t) \) » style="vertical-align:middle ; « >\(-2\sqrt{3}≈−3.5\) | \ (y (t) \) » style="vertical-align:middle ; « >-2 |
| \ (t \) » style="vertical-align:middle ; « >\(\frac{π}{6}\) | \ (x (t) \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.5\) | \ (y (t) \) » style="vertical-align:middle ; ">2 | \ (t \) » style="vertical-align:middle ; « >\(\frac{4π}{3}\) | \ (x (t) \) » style="vertical-align:middle ; « >−2 | \ (y (t) \) » style="vertical-align:middle ; « >\(−2\sqrt{3}≈−3.5\) |
| \ (t \) » style="vertical-align:middle ; « >\(\frac{π}{3}\) | \ (x (t) \) » style="vertical-align:middle ; ">2 | \ (y (t) \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.5\) | \ (t \) » style="vertical-align:middle ; « >\(\frac{3π}{2}\) | \ (x (t) \) » style="vertical-align:middle ; « >0 | \ (y (t) \) » style="vertical-align:middle ; « >−4 |
| \ (t \) » style="vertical-align:middle ; « >\(\frac{π}{2}\) | \ (x (t) \) » style="vertical-align:middle ; « >0 | \ (y (t) \) » style="vertical-align:middle ; « >4 | \ (t \) » style="vertical-align:middle ; « >\(\frac{5π}{3}\) | \ (x (t) \) » style="vertical-align:middle ; ">2 | \ (y (t) \) » style="vertical-align:middle ; « >\(−2\sqrt{3}≈−3.5\) |
| \ (t \) » style="vertical-align:middle ; « >\(\frac{2π}{3}\) | \ (x (t) \) » style="vertical-align:middle ; « >−2 | \ (y (t) \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.5\) | \ (t \) » style="vertical-align:middle ; « >\(\frac{11π}{6}\) | \ (x (t) \) » style="vertical-align:middle ; « >\(2\sqrt{3}≈3.5\) | \ (y (t) \) » style="vertical-align:middle ; « >-2 |
| \ (t \) » style="vertical-align:middle ; « >\(\frac{5π}{6}\) | \ (x (t) \) » style="vertical-align:middle ; « >\(−2\sqrt{3}≈−3.5\) | \ (y (t) \) » style="vertical-align:middle ; ">2 | \ (t \) » style="vertical-align:middle ; « >\(2π\) | \ (x (t) \) » style="vertical-align:middle ; « >4 | \ (y (t) \) » style="vertical-align:middle ; « >0 |
| \ (t \) » style="vertical-align:middle ; « >\(π\) | \ (x (t) \) » style="vertical-align:middle ; « >−4 | \ (y (t) \) » style="vertical-align:middle ; « >0 | \ (t \) » style="vertical-align:middle ; « > | \ (x (t) \) » style="vertical-align:middle ; « > | \ (y (t) \) » style="vertical-align:middle ; « > |
Le graphique de cette courbe plane apparaît dans le graphique suivant.
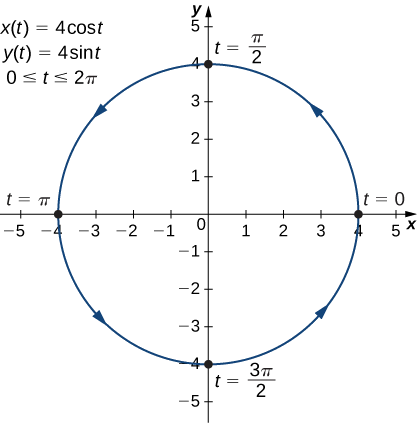
Il s'agit du graphe d'un cercle dont le rayon est\(4\) centré à l'origine, orienté dans le sens antihoraire. Le point de départ et le point d'arrivée de la courbe ont tous deux des coordonnées\((4,0)\).
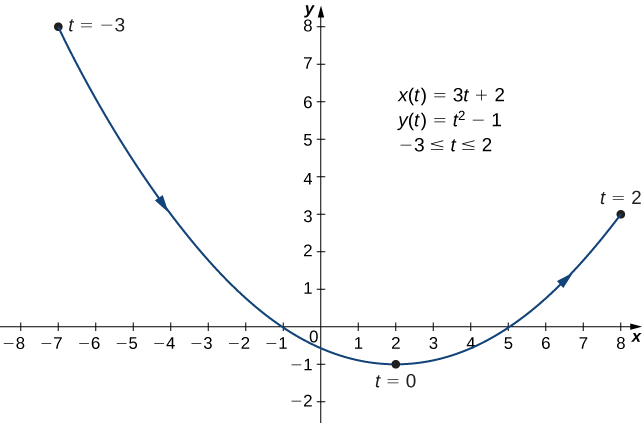
Esquissez la courbe décrite par les équations paramétriques
\[ x(t)=3t+2,\quad y(t)=t^2−1,\quad \text{for }−3≤t≤2. \nonumber \]
- Allusion
-
Créez un tableau des valeurs pour\(x(t)\) et\(y(t)\) en utilisant\(t\) les valeurs comprises entre\(−3\) et\(2\).
- Réponse
-
Élimination du paramètre
Pour mieux comprendre le graphe d'une courbe représentée de manière paramétrique, il est utile de réécrire les deux équations sous la forme d'une seule équation reliant les variables\(x\) et\(y\). Ensuite, nous pouvons appliquer toute connaissance préalable des équations des courbes dans le plan pour identifier la courbe. Par exemple, les équations décrivant la courbe plane dans l'exemple\(\PageIndex{1b}\) sont
\[\begin{align} x(t) &=t^2−3 \label{x1} \\[4pt] y(t) &=2t+1 \label{y1} \end{align} \]
sur la région\(-2 \le t \le 3.\)
Résolution de l'équation \ ref {y1} pour les\(t\) données
\[t=\dfrac{y−1}{2}. \nonumber \]
Cela peut être remplacé par l'équation \ ref {x1} :
\[\begin{align} x &=\left(\dfrac{y−1}{2}\right)^2−3 \\[4pt] &=\dfrac{y^2−2y+1}{4}−3 \\[4pt] &=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align} \]
L'équation \ ref {y2} est\(x\) décrite en fonction de\(y\). Ces étapes donnent un exemple d'élimination du paramètre. Le graphique de cette fonction est une parabole s'ouvrant vers la droite (Figure\(\PageIndex{4}\)). Rappelez-vous que la courbe plane a commencé à\((1,−3)\) et s'est terminée à\((6,7)\). Ces terminaisons étaient dues à la restriction du paramètre\(t\).
Éliminez le paramètre pour chacune des courbes planes décrites par les équations paramétriques suivantes et décrivez le graphique obtenu.
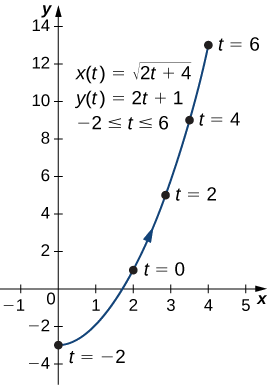
- \(x(t)=\sqrt{2t+4}, \quad y(t)=2t+1,\quad \text{for }−2≤t≤6\)
- \(x(t)=4\cos t, \quad y(t)=3\sin t,\quad \text{for }0≤t≤2π\)
Solution
a. Pour éliminer le paramètre, nous pouvons résoudre l'une ou l'autre des équations pour\(t\). Par exemple, la résolution de la première équation pour\(t\) donne
\[\begin{align*} x &=\sqrt{2t+4} \\[4pt] x^2 &=2t+4 \\[4pt] x^2−4 &=2t \\[4pt] t &=\dfrac{x^2−4}{2}. \end{align*}\]
Notez que lorsque nous mettons les deux côtés au carré, il est important de le noter\(x≥0\). \(t=\dfrac{x^2−4}{2}\)Substituer\(y(t)\) des rendements
\[ y(t)=2t+1 \nonumber \]
\[ y=2\left(\dfrac{x^2−4}{2}\right)+1 \nonumber \]
\[ y=x^2−4+1 \nonumber \]
\[ y=x^2−3. \nonumber \]
C'est l'équation d'une parabole s'ouvrant vers le haut. Il existe toutefois une restriction de domaine en raison des limites du paramètre\(t\). Quand\(t=−2\)\(x=\sqrt{2(−2)+4}=0\), et quand\(t=6\),\(x=\sqrt{2(6)+4}=4\). Le graphique de cette courbe plane suit.
b. Parfois, il est nécessaire d'être un peu créatif pour éliminer le paramètre. Les équations paramétriques de cet exemple sont
\[ x(t)=4 \cos t\nonumber \]
et
\[ y(t)=3 \sin t\nonumber \]
Il n'est pas conseillé de résoudre\(t\) directement l'une ou l'autre des équations car le sinus et le cosinus ne sont pas des fonctions biuni Cependant, diviser la première équation par\(4\) et la seconde équation par\(3\) (et supprimer le\(t\)) nous donne
\[ \cos t=\dfrac{x}{4}\nonumber \]
et
\[ \sin t=\dfrac{y}{3}.\nonumber \]
Utilisez maintenant l'identité pythagoricienne\(\cos^2t+\sin^2t=1\) et remplacez les expressions pour\(\sin t\) et\(\cos t\) par les expressions équivalentes en termes de\(x\) et\(y\). Cela donne
\[ \left(\dfrac{x}{4}\right)^2+\left(\dfrac{y}{3}\right)^2=1 \nonumber \]
\[ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1. \nonumber \]
Il s'agit de l'équation d'une ellipse horizontale centrée à l'origine, avec un demi-grand axe\(4\) et un demi-petit axe,\(3\) comme le montre le graphique suivant.
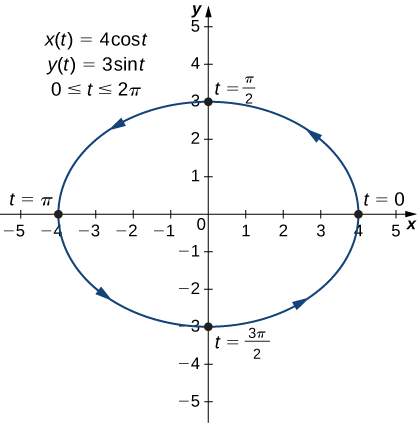
Au fur et\(0\) à mesure qu'il progresse de à\(2π\), un point de la courbe traverse l'ellipse une fois, dans le sens antihoraire. Rappelons dans l'ouverture de la section que l'orbite de la Terre autour du Soleil est également elliptique. Il s'agit d'un parfait exemple d'utilisation de courbes paramétrées pour modéliser un phénomène réel.
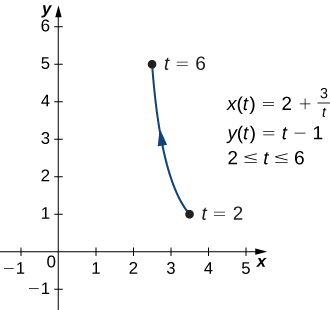
Éliminez le paramètre de la courbe plane définie par les équations paramétriques suivantes et décrivez le graphe obtenu.
\[ x(t)=2+\dfrac{3}{t}, \quad y(t)=t−1, \quad\text{for }2≤t≤6 \nonumber \]
- Allusion
-
Résolvez l'une des équations\(t\) et remplacez-la par l'autre.
- Réponse
-
\(x=2+\frac{3}{y+1},\)ou\(y=−1+\frac{3}{x−2}\). Cette équation décrit une partie d'une hyperbole rectangulaire centrée sur\((2,−1)\).
Jusqu'à présent, nous avons vu la méthode d'élimination du paramètre, en supposant que nous connaissons un ensemble d'équations paramétriques décrivant une courbe plane. Et si nous voulions commencer par l'équation d'une courbe et déterminer une paire d'équations paramétriques pour cette courbe ? C'est certainement possible et, en fait, il est possible de le faire de différentes manières pour une courbe donnée. Le processus est connu sous le nom de paramétrage d'une courbe.
Trouvez deux paires différentes d'équations paramétriques pour représenter le graphe de\(y=2x^2−3\).
Solution
Tout d'abord, il est toujours possible de paramétrer une courbe en la définissant\(x(t)=t\), puis en la\(x\) remplaçant par\(t\) dans l'équation de\(y(t)\). Cela donne le paramétrage
\[ x(t)=t, \quad y(t)=2t^2−3. \nonumber \]
Comme il n'y a aucune restriction sur le domaine dans le graphe d'origine, il n'y a aucune restriction sur les valeurs de\(t\).
Nous avons toute liberté dans le choix du second paramétrage. Par exemple, nous pouvons choisir\(x(t)=3t−2\). La seule chose que nous devons vérifier, c'est qu'aucune restriction n'est imposée\(x\), c'est-à-dire que la plage de nombres\(x(t)\) est entièrement réelle. C'est le cas pour\(x(t)=3t−2\). Depuis\(y=2x^2−3\), nous pouvons remplacer\(x(t)=3t−2\)\(x\). Cela donne
\[ y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6. \nonumber \]
Par conséquent, un second paramétrage de la courbe peut être écrit comme
\( x(t)=3t−2\)et\( y(t)=18t^2−24t+6.\)
Trouvez deux ensembles différents d'équations paramétriques pour représenter le graphe de\(y=x^2+2x\).
- Allusion
-
Suivez les étapes de l'exemple\(\PageIndex{3}\). N'oubliez pas que nous sommes libres de choisir le paramétrage pour\(x(t)\).
- Réponse
-
Une possibilité est\(x(t)=t, \quad y(t)=t^2+2t.\) Une autre possibilité est\(x(t)=2t−3, \quad y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.\) Il existe, en fait, un nombre infini de possibilités.
Cycloïdes et autres courbes paramétriques
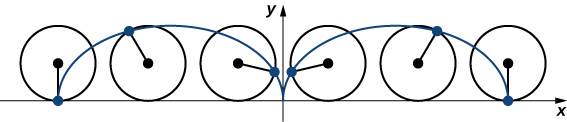
Imaginez-vous faire une balade à vélo à travers le pays. Les pneus restent en contact avec la route et tournent selon un schéma prévisible. Supposons maintenant qu'une fourmi très déterminée soit fatiguée après une longue journée et veuille rentrer chez elle. Il s'accroche donc sur le côté du pneu et fait un tour gratuit. Le chemin parcouru par cette fourmi sur une route droite est appelé cycloïde (Figure\( \PageIndex{8}\)). Une cycloïde générée par un cercle (ou une roue de vélo) de rayon a est donnée par les équations paramétriques
\[x(t)=a(t−\sin t), \quad y(t)=a(1−\cos t).\nonumber \]
Pour comprendre pourquoi cela est vrai, considérez la trajectoire empruntée par le centre de la roue. Le centre se déplace le long de\(x\) l'axe -à une hauteur constante égale au rayon de la roue. Si le rayon est\(a\), alors les coordonnées du centre peuvent être données par les équations
\[x(t)=at,\quad y(t)=a\nonumber \]
pour n'importe quelle valeur de\(t\). Ensuite, considérez la fourmi, qui tourne autour du centre le long d'un chemin circulaire. Si le vélo se déplace de gauche à droite, les roues tournent dans le sens des aiguilles d'une montre. Un paramétrage possible du mouvement circulaire de la fourmi (par rapport au centre de la roue) est donné par
\[\begin{align*} x(t) &=−a \sin t \\[4pt] y(t) &=−a\cos t.\end{align*}\]
(Le signe négatif est nécessaire pour inverser l'orientation de la courbe. Si le signe négatif n'était pas là, il faudrait imaginer que la roue tourne dans le sens antihoraire.) L'addition de ces équations donne les équations pour la cycloïde.
\[\begin{align*} x(t) &=a(t−\sin t) \\[4pt] y(t) &=a(1−\cos t ) \end{align*}\]
Supposons maintenant que la roue du vélo ne se déplace pas sur une route droite mais qu'elle se déplace à l'intérieur d'une roue plus grande, comme dans la Figure\( \PageIndex{9}\). Dans ce graphique, le cercle vert se déplace autour du cercle bleu dans le sens antihoraire. Un point sur le bord du cercle vert trace le graphe rouge, appelé hypocycloïde.
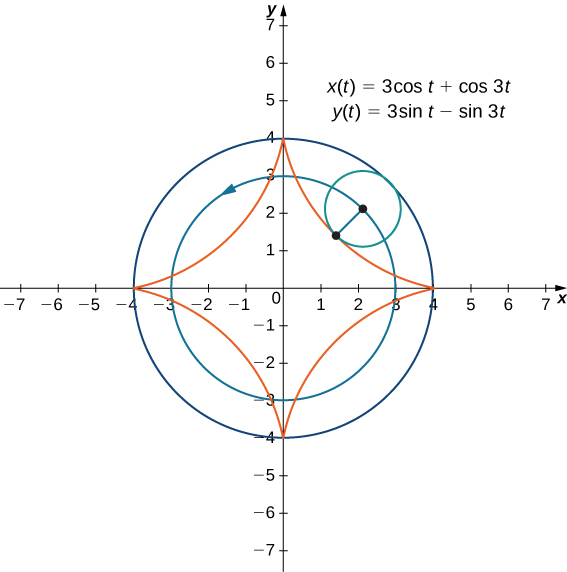
Les équations paramétriques générales pour un hypocycloïde sont
\[x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t \nonumber \]
\[y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t. \nonumber \]
Ces équations sont un peu plus compliquées, mais leur dérivation est un peu similaire aux équations de la cycloïde. Dans ce cas, nous supposons que le rayon du plus grand cercle est\(a\) et que le rayon du plus petit cercle est\(b\). Ensuite, le centre de la roue se déplace le long d'un cercle de rayon.\(a−b.\) Ce fait explique le premier terme de chaque équation ci-dessus. La période de la deuxième fonction trigonométrique dans les deux\(x(t)\) et\(y(t)\) est égale à\(\dfrac{2πb}{a−b}\).
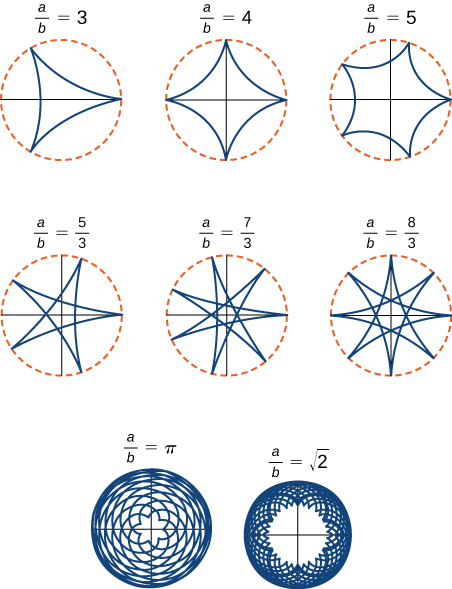
Le ratio\(\dfrac{a}{b}\) est lié au nombre de cuspides sur le graphique (les cuspides sont les coins ou les extrémités pointues du graphique), comme illustré à la figure\( \PageIndex{10}\). Ce ratio peut donner lieu à des graphiques très intéressants, selon que le ratio est rationnel ou non. La figure\(\PageIndex{9}\) correspond à\(a=4\) et\(b=1\). Le résultat est un hypocycloïde à quatre cuspides. La figure\(\PageIndex{10}\) montre d'autres possibilités. Les deux derniers hypocycloïdes ont des valeurs irrationnelles pour\(\dfrac{a}{b}\). Dans ces cas, les hypocycloïdes ont un nombre infini de cuspides, de sorte qu'ils ne reviennent jamais à leur point de départ. Ce sont des exemples de ce que l'on appelle des courbes de remplissage d'espace.
De nombreuses courbes planes en mathématiques portent le nom des personnes qui les ont étudiées pour la première fois, comme le folium de Descartes ou la spirale d'Archimède. Cependant, le nom le plus étrange pour une courbe est peut-être celui de la sorcière d'Agnesi. Pourquoi une sorcière ?
Maria Gaetana Agnesi (1718-1799) était l'une des rares femmes mathématiciennes reconnues de l'Italie du XVIIIe siècle. Elle a écrit un livre populaire sur la géométrie analytique, publié en 1748, qui comprenait une courbe intéressante qui avait été étudiée par Fermat en 1630. Le mathématicien Guido Grandi a montré en 1703 comment construire cette courbe, qu'il a ensuite appelée « versoria », terme latin désignant une corde utilisée en voile. Agnesi a utilisé le terme italien pour désigner cette corde, « versiera », mais en latin, ce même mot signifie « femme gobelin ». Lorsque le livre d'Agnesi a été traduit en anglais en 1801, le traducteur a utilisé le terme « sorcière » pour désigner la courbe, au lieu de corde. Depuis lors, le nom de « sorcière d'Agnesi » est resté gravé.
La sorcière d'Agnesi est une courbe définie comme suit : Commencez par un cercle de rayon a de telle sorte que les points\((0,0)\) et\((0,2a)\) soient des points sur le cercle (Figure\( \PageIndex{11}\)). Soit O l'origine. Choisissez n'importe quel autre point A du cercle et tracez la ligne sécante OA. Soit B le point par lequel la droite OA coupe la ligne horizontale\((0,2a)\). La ligne verticale passant par B croise la ligne horizontale passant par A au point P. Lorsque le point A varie, la trajectoire parcourue par le point P est la sorcière de la courbe d'Agnesi pour le cercle donné.
Les courbes de Witch of Agnesi ont des applications en physique, notamment pour la modélisation des vagues d'eau et des distributions de raies spectrales. En théorie des probabilités, la courbe décrit la fonction de densité de probabilité de la distribution de Cauchy. Dans ce projet, vous allez paramétrer ces courbes.
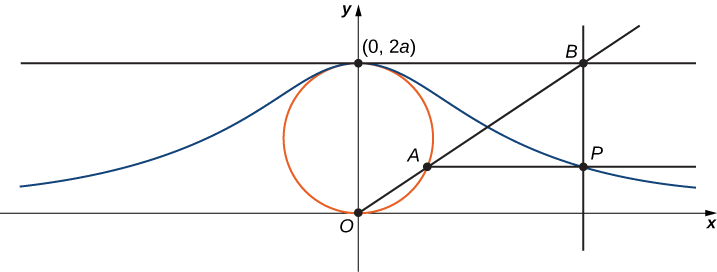
1. Sur la figure, étiquetez les points, les longueurs et les angles suivants :
a.\(C\) est le point de l'\(x\)axe -avec la même\(x\) coordonnée que\(A\).
b.\(x\) est la\(x\) coordonnée -de\(P\), et\(y\) est la\(y\) coordonnée -de\(P\).
c.\(E\) est le point\((0,a)\).
d.\(F\) est le point du segment de ligne\(OA\) tel que le segment de ligne\(EF\) soit perpendiculaire au segment de droite\(OA\).
e.\(b\) est la distance entre\(O\) et\(F\).
f.\(c\) est la distance entre\(F\) et\(A\).
g.\(d\) est la distance entre\(O\) et\(C\).
h.\(θ\) est la mesure de l'angle\(∠COA\).
L'objectif de ce projet est de paramétrer la sorcière en\(θ\) tant que paramètre. Pour ce faire, écrivez des équations pour\(x\) et\(y\) en termes de uniquement\(θ\).
2. Montrez ça\(d=\dfrac{2a}{\sin θ}\).
3. Notez que\(x=d\cos θ\). Montrez ça\(x=2a\cot θ\). Lorsque vous faites cela, vous aurez paramétré la\(x\) coordonnée -de la courbe par rapport à\(θ\). Si vous pouvez obtenir une équation similaire pour\(y\), vous aurez paramétré la courbe.
4. En termes de\(θ\), quel est l'angle\(∠EOA\) ?
5. Montrez ça\(b+c=2a\cos\left(\frac{π}{2}−θ\right)\).
6. Montrez ça\(y=2a\cos\left(\frac{π}{2}−θ\right)\sin θ\).
7. Montrez ça\(y=2a\sin^2θ\). Vous avez maintenant\(y\) paramétré la coordonnée de la courbe par rapport à\(θ\).
8. Concluez qu'un paramétrage de la courbe de commutation donnée est
\[x=2a\cot θ, \quad y=2a \sin^2θ, \quad\text{for }−∞<θ<∞. \nonumber \]
9. Utilisez votre paramétrage pour montrer que la courbe de sorcière donnée est le graphe de la fonction\(f(x)=\dfrac{8a^3}{x^2+4a^2}\).
Plus tôt dans cette section, nous avons examiné les équations paramétriques d'une cycloïde, c'est-à-dire la trajectoire tracée par un point sur le bord d'une roue lorsque celle-ci roule le long d'une trajectoire droite. Dans ce projet, nous examinons deux variantes différentes de la cycloïde, appelées cycloïdes curtate et cycloïde allongée.
Revoyons d'abord la dérivation des équations paramétriques pour une cycloïde. Rappelons que nous avons considéré une fourmi tenace qui essayait de rentrer chez elle en s'accrochant au bord d'un pneu de vélo. Nous avons supposé que la fourmi avait grimpé sur le pneu au bord, là où le pneu touche le sol. Lorsque la roue roule, la fourmi se déplace avec le bord du pneu (Figure\(\PageIndex{12}\)).
Comme nous l'avons vu, nous disposons d'une grande flexibilité lors du paramétrage d'une courbe. Dans ce cas, nous laissons notre paramètre t représenter l'angle de rotation du pneu. En regardant la figure\( \PageIndex{12}\), nous voyons qu'après que le pneu a pivoté d'un angle de\(t\), la position du centre de la roue\(C=(x_C,y_C)\), est donnée par
\(x_C=at\)et\(y_C=a\).
De plus, en\(A=(x_A,y_A)\) indiquant la position de la fourmi, nous notons que
\(x_C−x_A=a\sin t\)et\(y_C−y_A=a \cos t\)
Alors
\[x_A=x_C−a\sin t=at−a\sin t=a(t−\sin t) \nonumber \]
\[y_A=y_C−a\cos t=a−a\cos t=a(1−\cos t). \nonumber \]
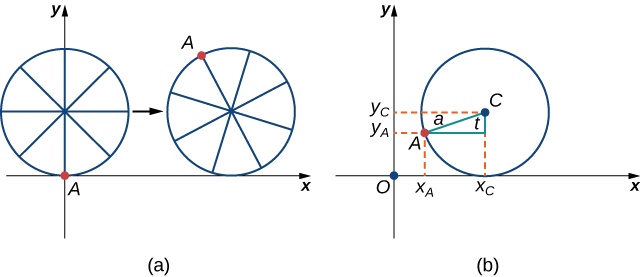
Notez qu'il s'agit des mêmes représentations paramétriques que nous avions auparavant, mais nous avons maintenant attribué une signification physique à la variable paramétrique\(t\).
Au bout d'un moment, la fourmi a le vertige à force de tourner en rond sur le bord du pneu. Il remonte donc l'un des rayons vers le centre de la roue. En montant vers le centre de la roue, la fourmi a changé de trajectoire. La nouvelle trajectoire présente moins de mouvements de haut en bas et est appelée cycloïde curtate (Figure\( \PageIndex{13}\)). Comme le montre la figure, on désigne par b la distance le long du rayon entre le centre de la roue et la fourmi. Comme précédemment, nous l'avons laissé représenter l'angle de rotation du pneu. De plus, nous laissons\(C=(x_C,y_C)\) représenter la position du centre de la roue et\(A=(x_A,y_A)\) représenter la position de la fourmi.
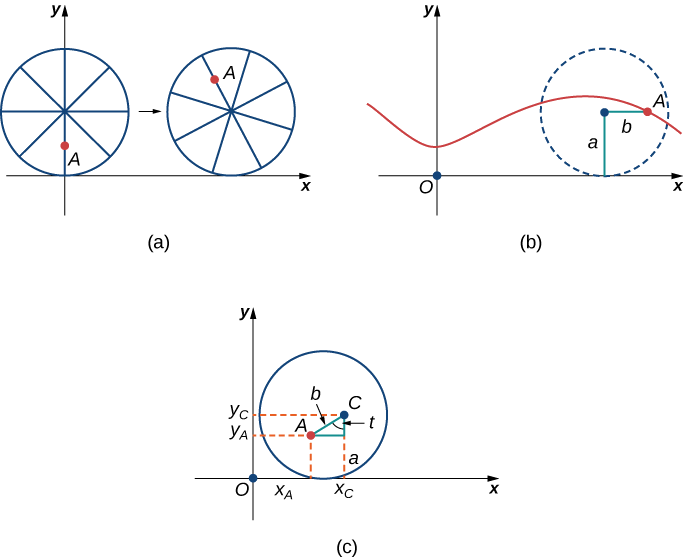
1. Quelle est la position du centre de la roue une fois que le pneu a pivoté d'un angle de\(t\) ?
2. Utilisez la géométrie pour rechercher des expressions pour\(x_C−x_A\) et pour\(y_C−y_A\).
3. Sur la base de vos réponses aux parties 1 et 2, quelles sont les équations paramétriques représentant la cycloïde curtate ?
Une fois que la tête de la fourmi s'est dégagée, il se rend compte que le cycliste a fait un virage et s'éloigne maintenant de chez lui. Il dépose donc le pneu du vélo et regarde autour de lui. Heureusement, il y a un ensemble de voies ferrées à proximité, qui reprennent la bonne direction. La fourmi se dirige donc vers les voies ferrées pour attendre. Au bout d'un moment, un train passe, se dirigeant dans la bonne direction, et il parvient à sauter et à attraper le bord de la roue du train (sans se faire écraser !).
La fourmi craint toujours d'avoir le vertige, mais la roue du train est glissante et n'a pas de rayons à gravir. Il décide donc de s'accrocher au bord de la roue et d'espérer que tout ira pour le mieux. Désormais, les roues des trains sont munies d'une bride qui permet à la roue de rouler sur les voies. Ainsi, dans ce cas, puisque la fourmi est accrochée au bord même de la bride, la distance entre le centre de la roue et la fourmi est en fait supérieure au rayon de la roue (Figure\(\PageIndex{14}\)).
La configuration ici est essentiellement la même que lorsque la fourmi a grimpé sur le rayon de la roue du vélo. On désigne par b la distance entre le centre de la roue et la fourmi, et on laisse t représenter l'angle de rotation du pneu. De plus, nous laissons\(C=(x_C,y_C)\) représenter la position du centre de la roue et\(A=(x_A,y_A)\) représenter la position de la fourmi (Figure\( \PageIndex{14}\)).
Lorsque la distance entre le centre de la roue et la fourmi est supérieure au rayon de la roue, sa trajectoire de mouvement est appelée cycloïde allongée. Un graphique d'une cycloïde allongée est représenté sur la figure.
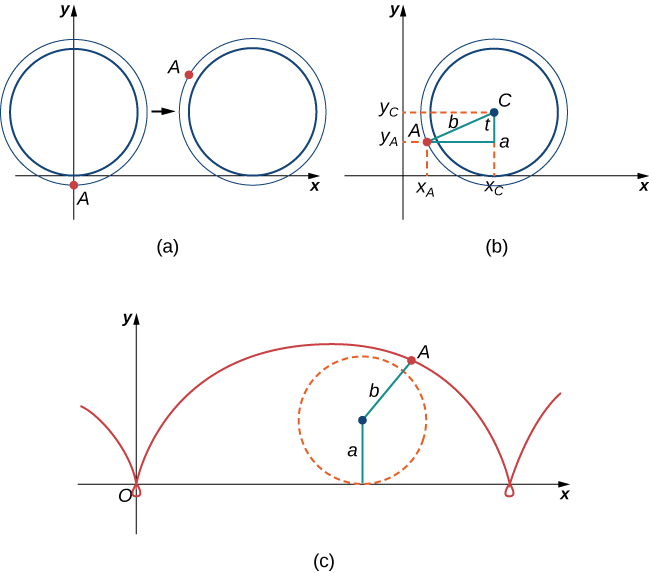
4. En utilisant la même approche que celle que vous avez utilisée dans les parties 1 à 3, trouvez les équations paramétriques de la trajectoire de mouvement de la fourmi.
5. Que remarquez-vous dans votre réponse à la partie 3 et votre réponse à la partie 4 ?
Remarquez que la fourmi se déplace parfois vers l'arrière (les « boucles » sur le graphique), même si le train continue d'avancer. Il sera probablement très étourdi en rentrant chez lui !
Concepts clés
- Les équations paramétriques constituent un moyen pratique de décrire une courbe. Un paramètre peut représenter le temps ou une autre quantité significative.
- Il est souvent possible d'éliminer le paramètre d'une courbe paramétrée pour obtenir une fonction ou une relation décrivant cette courbe.
- Il existe toujours plusieurs manières de paramétrer une courbe.
- Les équations paramétriques peuvent décrire des courbes complexes difficiles voire impossibles à décrire à l'aide de coordonnées rectangulaires.
Lexique
- cycloïde
- la courbe tracée par un point sur la jante d'une roue circulaire lorsque la roue roule le long d'une ligne droite sans glisser
- cuspide
- une extrémité pointue ou une partie où deux courbes se rencontrent
- orientation
- la direction dans laquelle un point se déplace sur un graphique lorsque le paramètre augmente
- paramètre
- une variable indépendante qui\(y\) dépend\(x\) à la fois d'une courbe paramétrique ; généralement représentée par la variable\(t\)
- courbe paramétrique
- le graphe des équations paramétriques\(x(t)\) et\(y(t)\) sur un intervalle\(a≤t≤b\) combiné aux équations
- équations paramétriques
- les équations\(x=x(t)\) et\(y=y(t)\) qui définissent une courbe paramétrique
- paramétrage d'une courbe
- réécriture de l'équation d'une courbe définie par une fonction\(y=f(x)\) sous forme d'équations paramétriques


