Skip to main content
Global

10.1E : Exercices pour la section 10.1

  1. Last updated
  2. Save as PDF
  • Page ID
    197127

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 4, indiquez si chaque déclaration est vraie ou donnez un exemple pour montrer qu'elle est fausse.

    1) Si\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge, alors\(a_nx^n→0\) comme\(n→∞.\)

    Réponse
    C'est vrai. Si une série converge, ses termes ont tendance à être nuls.

    2)\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge vers n'\(x=0\)importe quel nombre réel\(a_n\).

    3) Quelle que soit la séquence\(a_n\), il y en a toujours une\(R>0\), peut-être très petite, qui\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge vers\((−R,R)\).

    Réponse
    Faux. Cela impliquerait que\(a_nx^n→0\) pour\(|x|<R\). Si\(a_n=n^n\), alors\(a_nx^n=(nx)^n\) n'a pas tendance à zéro pour aucun\(x≠0\).

    4) S'il\(\displaystyle \sum_{n=1}^∞a_nx^n\) a un rayon de convergence\(R>0\) et si\(|b_n|≤|a_n|\) pour tous\(n\), alors le rayon de convergence de\(\displaystyle \sum_{n=1}^∞b_nx^n\) est supérieur ou égal à\(R\).

    5) Supposons que cela\(\displaystyle \sum_{n=0}^∞a_n(x−3)^n\) converge vers\(x=6\). Sur lequel des points suivants les séries doivent-elles également converger ? Utilisez le fait que si elle\(\displaystyle \sum a_n(x−c)^n\) converge vers\(x\), alors elle converge en tout point\(c\) plus proche de\(x\).

    un.\(x=1\)

    b.\(x=2\)

    c.\(x=3\)

    d.\(x=0\)

    e.\(x=5.99\)

    f).\(x=0.000001\)

    Réponse
    Il doit converger vers\((0,6]\) et donc vers : a.\(x=1\)\(x=2\) ; b.\(x=3\) ; c.\(x=0\) ; d.\(x=5.99\) ; e. ; et\(x=0.000001\) f.

    6) Supposons que cela\(\displaystyle \sum_{n=0}^∞a_n(x+1)^n\) converge vers\(x=−2\). Sur lequel des points suivants les séries doivent-elles également converger ? Utilisez le fait que si elle\(\displaystyle \sum a_n(x−c)^n\) converge vers\(x\), alors elle converge en tout point\(c\) plus proche de\(x\).

    un.\(x=2\)

    b.\(x=−1\)

    c.\(x=−3\)

    d.\(x=0\)

    e.\(x=0.99\)

    f).\(x=0.000001\)

    Dans les exercices suivants, supposons\(\left|\dfrac{a_{n+1}}{a_n}\right|→1\) que\(n→∞.\) Trouvez le rayon de convergence pour chaque série.

    7)\(\displaystyle \sum_{n=0}^∞a_n2^nx^n\)

    Réponse
    \(\left|\dfrac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}\right| =2|x|\left|\dfrac{a_{n+1}}{a_n}\right|→2|x|\)donc\(R=\frac{1}{2}\)

    8)\(\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}\)

    9)\(\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}\)

    Réponse
    \(\left|\dfrac{a_{n+1}(\dfrac{π}{e})^{n+1}x^{n+1}}{a_n(\dfrac{π}{e})^nx^n}\right| =\dfrac{π|x|}{e}\left|\dfrac{a_{n+1}}{a_n}\right|→\dfrac{π|x|}{e}\)donc\(R=\frac{e}{π}\)

    10)\(\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}\)

    11)\(\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}\)

    Réponse
    \(\left|\dfrac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}\right| =|x^2|\left|\dfrac{a_{n+1}}{a_n}\right|→|x^2|\)donc\(R=1\)

    (12)\(\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}\)

    Dans les exercices 13 à 22, déterminez le rayon de convergence\(R\) et l'intervalle de convergence pour\(\displaystyle \sum a_nx^n\) les coefficients donnés\(a_n\).

    13)\(\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}\)

    Réponse
    \(a_n=\dfrac{2^n}{n}\)Donc\(\dfrac{a_{n+1}x}{a_n}→2x\). Donc\(R=\frac{1}{2}\). Quand\(x=\frac{1}{2}\) la série est harmonique et diverge. Lorsque\(x=−\frac{1}{2}\) la série alterne harmonique et converge. L'intervalle de convergence est\(I=\big[−\frac{1}{2},\frac{1}{2}\big)\).

    (14)\(\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}\)

    (15)\(\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}\)

    Réponse
    \(a_n=\dfrac{n}{2^n}\)Donc\(\dfrac{a_{n+1}x}{a_n}→\dfrac{x}{2}\) donc\(R=2\). Lorsque\(x=±2\) la série diverge par le test de divergence. L'intervalle de convergence est\(I=(−2,2)\).

    16)\(\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}\)

    17)\(\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}\)

    Réponse
    \(a_n=\dfrac{n^2}{2^n}\)donc\(R=2\). Lorsque\(x=±2\) la série diverge par le test de divergence. L'intervalle de convergence est\(I=(−2,2).\)

    18)\(\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}\)

    19)\(\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}\)

    Réponse
    \(a_k=\dfrac{π^k}{k^π}\)donc\(R=\frac{1}{π}\). Lorsque\(x=±\frac{1}{π}\) la série est une\(p\) série absolument convergente. L'intervalle de convergence est\(I=\left[−\frac{1}{π},\frac{1}{π}\right].\)

    (20)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}\)

    (21)\(\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}\)

    Réponse
    \(a_n=\dfrac{10^n}{n!},\dfrac{a_{n+1}x}{a_n}=\dfrac{10x}{n+1}→0<1\)donc la série converge pour tous\(x\) selon le test du ratio et\(I=(−∞,∞)\).

    (22)\(\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\ln(2n)}\)

    Dans les exercices 23 à 28, déterminez le rayon de convergence de chaque série.

    23)\(\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}\)

    Réponse
    \(a_k=\dfrac{(k!)^2}{(2k)!}\)donc\(\dfrac{a_{k+1}}{a_k}=\dfrac{(k+1)^2}{(2k+2)(2k+1)}→\dfrac{1}{4}\) donc\(R=4\)

    (24)\(\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}\)

    25)\(\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k\)

    Réponse
    \(a_k=\dfrac{k!}{1⋅3⋅5⋯(2k−1)}\)donc\(\dfrac{a_{k+1}}{a_k}=\dfrac{k+1}{2k+1}→\dfrac{1}{2}\) donc\(R=2\)

    (26)\(\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k\)

    27)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}\) où\((^n_k)=\dfrac{n!}{k!(n−k)!}\)

    Réponse
    \(a_n=\dfrac{1}{(^{2n}_n)}\)donc\(\dfrac{a_{n+1}}{a_n}=\dfrac{\big((n+1)!\big)^2}{(2n+2)!}\dfrac{2n!}{(n!)^2}=\dfrac{(n+1)^2}{(2n+2)(2n+1)}→\dfrac{1}{4}\) donc\(R=4\)

    (28)\(\displaystyle \sum_{n=1}^∞\sin^2nx^n\)

    Dans les exercices 29 à 32, utilisez le test du ratio pour déterminer le rayon de convergence de chaque série.

    (29)\(\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n\)

    Réponse
    \(\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\dfrac{1}{27}\)donc\(R=27\)

    (30)\(\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n\)

    31)\(\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n\)

    Réponse
    \(a_n=\dfrac{n!}{n^n}\)donc\(\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)!}{n!}\dfrac{n^n}{(n+1)^{n+1}}=(\dfrac{n}{n+1})^n→\dfrac{1}{e}\) donc\(R=e\)

    32)\(\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n\)

    Dans les exercices suivants, étant donné que\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\) la convergence est activée\((−1,1)\), trouvez la série de puissances pour chaque fonction dont le centre est donné\(a,\) et identifiez son intervalle de convergence.

    33)\(f(x)=\dfrac{1}{x};a=1\) (Astuce :\(\dfrac{1}{x}=\dfrac{1}{1−(1−x)})\)

    Réponse
    \(\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n\)sur\(I=(0,2)\)

    34)\(f(x)=\dfrac{1}{1−x^2};a=0\)

    35)\(f(x)=\dfrac{x}{1−x^2};a=0\)

    Réponse
    \(\displaystyle \sum_{n=0}^∞x^{2n+1}\)sur\(I=(−1,1)\)

    36)\(f(x)=\dfrac{1}{1+x^2};a=0\)

    (37)\(f(x)=\dfrac{x^2}{1+x^2};a=0\)

    Réponse
    \(\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}\)sur\(I=(−1,1)\)

    38)\(f(x)=\dfrac{1}{2−x};a=1\)

    39)\(f(x)=\dfrac{1}{1−2x};a=0.\)

    Réponse
    \(\displaystyle \sum_{n=0}^∞2^nx^n\)sur\(\left(−\frac{1}{2},\frac{1}{2}\right)\)

    40)\(f(x)=\dfrac{1}{1−4x^2};a=0\)

    41)\(f(x)=\dfrac{x^2}{1−4x^2};a=0\)

    Réponse
    \(\displaystyle \sum_{n=0}^∞4^nx^{2n+2}\)sur\(\left(−\frac{1}{2},\frac{1}{2}\right)\)

    (42)\(f(x)=\dfrac{x^2}{5−4x+x^2};a=2\)

    Utilisez le résultat de l'exercice 43 pour déterminer le rayon de convergence de la série donnée dans les exercices suivants (44 - 47).

    43) Expliquez pourquoi, si c'est\(|a_n|^{1/n}→r>0,\) le cas, à\(|a_nx^n|^{1/n}→|x|r<1\) tout moment\(|x|<\frac{1}{r}\) et, par conséquent, le rayon de convergence de\(\displaystyle \sum_{n=1}^∞a_nx^n\) is\(R=\frac{1}{r}\).

    Réponse
    \(|a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r\)au\(|x|r<1\) fur\(n→∞\) et à mesure\(|x|<\frac{1}{r}\). Par conséquent,\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge lorsqu'il est\(|x|<\frac{1}{r}\) soumis au test\(n^{\text{th}}\) root.

    44)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}\)

    45)\(\displaystyle \sum_{k=1}^∞\left(\frac{k−1}{2k+3}\right)^kx^k\)

    Réponse
    \(a_k=\left(\dfrac{k−1}{2k+3}\right)^k\)donc\((a_k)^{1/k}→\frac{1}{2}<1\) donc\(R=2\)

    46)\(\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k\)

    47)\(\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n\)

    Réponse
    \(a_n=(n^{1/n}−1)^n\)donc\((a_n)^{1/n}→0\) donc\(R=∞\)

    48)\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) Supposons qu'\(a_n=0\)il\(n\) soit égal. Expliquez pourquoi\(p(x)=p(−x).\)

    49) Supposons que c'est\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) tel\(a_n=0\) que\(n\) c'est étrange. Expliquez pourquoi\(p(x)=−p(−x).\)

    Réponse
    Nous pouvons réécrire\(\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}\) et\(p(x)=p(−x)\) depuis\(x^{2n+1}=−(−x)^{2n+1}\).

    50) Supposons que cela\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) converge vers\((−1,1]\). Détermine l'intervalle de convergence de\(p(Ax)\).

    51) Supposons que cela\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) converge vers\((−1,1]\). Détermine l'intervalle de convergence de\(p(2x−1)\).

    Réponse
    Si\(x∈[0,1],\)\(y=2x−1∈[−1,1]\) alors c'est\(\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n\) le cas.

    Dans les exercices suivants, supposons que\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) cela correspond à\(\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1\) où\(a_n≥0\) pour chacun\(n\). Indiquez si chaque série converge vers l'intervalle\((−1,1)\) complet ou s'il n'y a pas suffisamment d'informations pour tirer une conclusion. Utilisez le test de comparaison le cas échéant.

    52)\(\displaystyle \sum_{n=0}^∞a_nx^{2n}\)

    53)\(\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}\)

    Réponse
    Converge vers l'\((−1,1)\)aide du test du ratio

    54)\(\displaystyle \sum_{n=0}^∞a_{2n}x^n\) (Astuce :\(x=±\sqrt{x^2}\))

    55)\(\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}\) (Indice : laissez-le\(b_k=a_k\)\(k=n^2\) pour certains\(n\), sinon\(b_k=0\).)

    Réponse
    Considérez la série\(\displaystyle \sum b_kx^k\) où,\(b_k=a_k\) si\(k=n^2\) et\(b_k=0\) sinon. C'est\(b_k≤a_k\) ainsi que la série converge vers\((−1,1)\) le test de comparaison.

    56) Supposons qu'il\(p(x)\) s'agisse d'un polynôme de degré\(N\). Détermine le rayon et l'intervalle de convergence de\(\displaystyle \sum_{n=1}^∞p(n)x^n\).

    57) [T] Tracez les graphes de\(\dfrac{1}{1−x}\) et des sommes partielles\(\displaystyle S_N=\sum_{n=0}^Nx^n\) pour\(n=10,20,30\) l'intervalle\([−0.99,0.99]\). Commentez l'approximation de près et de\(S_N\) près\(\dfrac{1}{1−x}\) au fur\(x=−1\) et à\(x=1\) mesure que l'on\(N\) augmente.

    Réponse

    L'approximation est plus précise à proximité\(x=−1\). Les sommes partielles suivent de\(\dfrac{1}{1−x}\) plus près au fur et à mesure des\(N\) augmentations, mais elles ne sont jamais exactes à proximité,\(x=1\) car les séries divergent

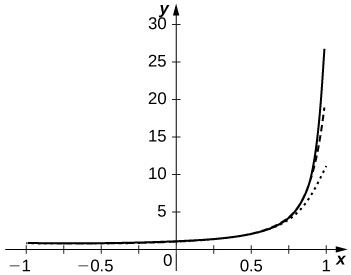
    Cette figure est le graphique de y = 1/ (1-x), qui est une courbe croissante avec une asymptote verticale à 1.

    58) [T] Tracez les graphes de\(−\ln(1−x)\) et des sommes partielles\(\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}\) pour\(n=10,50,100\) l'intervalle\([−0.99,0.99]\). Commentez le comportement des sommes proches\(x=−1\) et proches de\(x=1\) l'\(N\)augmentation.

    59) [T] Tracez les graphes des sommes partielles\(\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}\) pour\(n=10,50,100\) l'intervalle\([−0.99,0.99]\). Commentez le comportement des sommes proches\(x=−1\) et proches de\(x=1\) l'\(N\)augmentation.

    Réponse

    L'approximation semble se stabiliser rapidement à proximité des deux\(x=±1\).

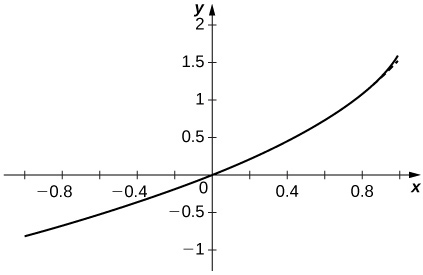
    Cette figure est le graphique de y = -ln (1-x) qui est une courbe croissante passant par l'origine.

    60) [T] Tracez les graphes des sommes partielles\(\displaystyle S_N=\sum_{n=1}^N(\sin n) x^n\) pour\(n=10,50,100\) l'intervalle\([−0.99,0.99]\). Commentez le comportement des sommes proches\(x=−1\) et proches de\(x=1\) l'\(N\)augmentation.

    61) [T] Tracez les graphes des sommes partielles\(\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}\) pour\(n=3,5,10\) l'intervalle\([−2π,2π]\). Expliquez comment ces diagrammes se\(\sin x\) rapprochent des\(N\) augmentations.

    Réponse

    Les courbes polynomiales ont des racines proches de celles\(\sin x\) allant jusqu'à leur degré, puis les polynômes divergent\(\sin x\).

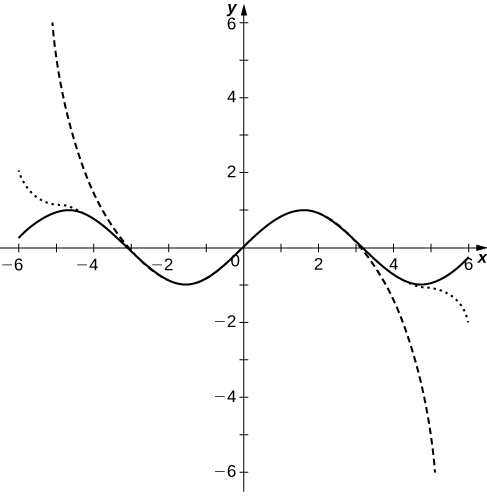
    Cette figure est le graphique des sommes partielles de (-1) ^n fois x^ (2n+1) divisée par (2n+1) ! Pour n = 3,5,10. Les courbes se rapprochent de la courbe sinusoïdale proche de l'origine, puis se séparent à mesure que les courbes s'éloignent de l'origine.

    62) [T] Tracez les graphes des sommes partielles\(\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}\) pour\(n=3,5,10\) l'intervalle\([−2π,2π]\). Expliquez comment ces diagrammes se\(\cos x\) rapprochent des\(N\) augmentations.