10.1 : Série Power et fonctions

Last updated
Save as PDF

Page ID: 197117

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Identifiez une série de puissance et donnez-en des exemples.
Déterminez le rayon de convergence et l'intervalle de convergence d'une série de puissances.
Utilisez une série de puissances pour représenter une fonction.

Une série de puissance est un type de série dont les termes impliquent une variable. Plus précisément, si la variable est$x$, alors tous les termes de la série impliquent des puissances de$x$. Par conséquent, une série de puissances peut être considérée comme un polynôme infini. Les séries de puissance sont utilisées pour représenter des fonctions communes et également pour définir de nouvelles fonctions. Dans cette section, nous définissons les séries de puissances et montrons comment déterminer quand une série de puissances converge et quand elle diverge. Nous montrons également comment représenter certaines fonctions à l'aide de séries de puissance.

Forme d'une série Power

Une série du formulaire

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]

où$x$ est une variable et les coefficients$c_n$ sont des constantes, est connue sous le nom de série de puissance. La série

\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]

est un exemple de série Power. Comme cette série est une série géométrique avec ratio$r=|x|$, nous savons qu'elle converge si$|x|<1$ et diverge si$|x|≥1.$

Définition$\PageIndex{1}$: Power Series

Une série du formulaire

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]

est une série de puissances centrée sur$x=0.$ une série A de la forme

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

est une série de puissance centrée sur$x=a$.

Pour que cette définition soit précise, nous stipulons cela$x^0=1$ et$(x−a)^0=1$ même quand$x=0$ et$x=a$, respectivement.

La série

\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]

\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]

sont toutes deux des séries de puissance centrées sur$x=0.$ La série

\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]

est une série de puissance centrée sur$x=2$.

Convergence d'une série Power

Comme les termes d'une série de puissances impliquent une variable$x$, la série peut converger pour certaines valeurs de$x$ et diverger pour d'autres valeurs de$x$. Pour une série de puissance centrée sur$x=a$, la valeur de la série at$x=a$ est donnée par$c_0$. Par conséquent, une série de puissances converge toujours en son centre. Certaines séries de puissance convergent uniquement à cette valeur de$x$. Cependant, la plupart des séries de puissance convergent pour plus d'une valeur de$x$. Dans ce cas, la série de puissances converge pour tous les nombres réels$x$ ou converge pour tous$x$ dans un intervalle fini. Par exemple, la série géométrique$\displaystyle \sum_{n=0}^∞x^n$ converge pour tous$x$ dans l'intervalle$(−1,1)$, mais diverge pour tous ceux qui se trouvent$x$ en dehors de cet intervalle. Nous résumons maintenant ces trois possibilités pour une série de puissance générale.

Remarque$\PageIndex{1}$: Convergence of a Power Series

Considérez la série Power$\displaystyle \sum_{n=0}^∞c_n(x−a)^n.$ La série répond exactement à l'une des propriétés suivantes :

La série converge$x=a$ et diverge pour tous$x≠a.$
La série converge pour tous les nombres réels$x$.
Il existe un nombre réel$R>0$ tel que la série converge si$|x−a|<R$ et diverge si$|x−a|>R$. Aux valeurs$x$ où |X−A|=R, la série peut converger ou diverger.

Une preuve

Supposons que la série de puissance soit centrée sur$a=0$. (Pour une série centrée sur une valeur autre que zéro, le résultat suit en laissant$y=x−a$ et en considérant la série

\[ \sum_{n=1}^∞c_ny^n. \nonumber \]

Nous devons d'abord prouver le fait suivant :

S'il existe un nombre réel$d≠0$ tel que celui qui$\displaystyle \sum_{n=0}^∞c_nd^n$ converge, alors la série$\displaystyle \sum_{n=0}^∞c_nx^n$ converge absolument pour tous de$x$ telle sorte que$|x|<|d|.$

Puisque$\displaystyle \sum_{n=0}^∞c_nd^n$ converge, le neuvième terme$c_nd^n→0$ était$n→∞$. Par conséquent, il existe un entier$N$ tel que$|c_nd^n|≤1$ pour toute$n≥N.$ écriture

\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]

nous concluons que, pour tout N≥N,

\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]

La série

\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]

est une série géométrique qui converge si$|\dfrac{x}{d}|<1.$ Par conséquent, par le test de comparaison, nous concluons qu'elle converge$\displaystyle \sum_{n=N}^∞c_nx^n$ également pour$|x|<|d|$. Comme nous pouvons ajouter un nombre fini de termes à une série convergente, nous concluons que$\displaystyle \sum_{n=0}^∞c_nx^n$ converge pour$|x|<|d|.$

Avec ce résultat, nous pouvons maintenant prouver le théorème. Considérez la série

\[\sum_{n=0}^∞a_nx^n \nonumber \]

et$S$ soit l'ensemble des nombres réels pour lesquels la série converge. Supposons que l'ensemble$S={0}.$ Ensuite, la série tombe dans le cas i.

Supposons que l'ensemble$S$ soit l'ensemble de tous les nombres réels. La série relève alors du cas ii. Supposons que$S≠{0}$ et ne$S$ soit pas l'ensemble des nombres réels. Il existe alors un nombre réel$x*≠0$ tel que la série ne converge pas. Ainsi, les séries ne peuvent pas converger pour une$x$ telle chose$|x|>|x*|$. Par conséquent, l'ensemble$S$ doit être un ensemble borné, ce qui signifie qu'il doit avoir la plus petite borne supérieure. (Ce fait découle de la propriété Least Upper Bound pour les nombres réels, qui dépasse le cadre de ce texte et est abordée dans de véritables cours d'analyse.) Appelez cela la plus petite borne supérieure$R$. Depuis$S≠{0}$, le numéro$R>0$. Par conséquent, la série converge pour tous de$x$ telle sorte que$|x|<R,$ la série tombe dans le cas iii.

□

Si une série$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ tombe dans le cas iii. de Note, alors la série converge pour tous de$x$ telle sorte que$|x−a|<R$ pour certains$R>0$, et diverge pour tous de$x$ telle sorte que$|x−a|>R$. La série peut converger ou diverger aux valeurs$x$ où$|x−a|=R$. L'ensemble de valeurs$x$ pour lequel la série$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ converge est appelé intervalle de convergence. Étant donné que la série diverge pour toutes les valeurs$x$ où$|x−a|>R$, la longueur de l'intervalle est$2R$, et donc, le rayon de l'intervalle est$R$. La valeur$R$ est appelée rayon de convergence. Par exemple, étant donné que la série$\displaystyle \sum_{n=0}^∞x^n$ converge pour toutes les valeurs$x$ de l'intervalle$(−1,1)$ et diverge pour toutes les valeurs$|x|≥1$, de$x$ telle sorte que l'intervalle de convergence de cette série est$(−1,1)$. Puisque la longueur de l'intervalle est$2$, le rayon de convergence est$1$.

Définition : rayon de convergence

Pensez à la série Power$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$. L'ensemble des nombres réels$x$ où la série converge est l'intervalle de convergence. S'il existe un nombre réel$R>0$ tel que la série converge pour$|x−a|<R$ et diverge pour$|x−a|>R,$, alors$R$ est le rayon de convergence. Si la série ne converge que vers$x=a$, nous disons que le rayon de convergence est$R=0$. Si la série converge pour tous les nombres réels$x$, nous disons que le rayon de convergence est$R=∞$ (Figure$\PageIndex{1}$).

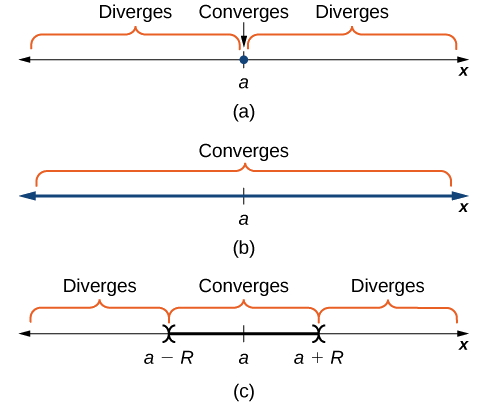
Cette figure comporte trois lignes numériques, chacune étiquetée par un x. Au milieu de chaque ligne numérique se trouve un point marqué a. La première ligne numérique a des « diverges » sur toute la ligne à gauche de a et « diverge » sur la ligne située à droite de a. Au point a lui-même, elle est étiquetée comme « converge ». La deuxième ligne numérique comporte des « convergences » étiquetées pour l'ensemble de la ligne. La troisième ligne numérique comporte des points marqués à a-R, a et a+R. À gauche de a-R, la ligne numérique est étiquetée « diverge ». Entre a-R et a+R, la ligne numérique est étiquetée « converge » et à droite de A+R, la ligne numérique est étiquetée « diverge ». — Figure$\PageIndex{1}$ : Pour une série, le$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ graphe (a) montre un rayon de convergence à$R=0$, le graphe (b) montre un rayon de convergence à$R=∞$ et le graphe (c) montre un rayon de convergence à$R$. Pour le graphique (c), nous notons que les séries peuvent ou non converger aux extrémités$x=a+R$ et$x=a−R$.

Pour déterminer l'intervalle de convergence d'une série de puissances, nous appliquons généralement le test du ratio. Dans l'exemple$\PageIndex{1}$, nous montrons les trois possibilités différentes illustrées dans la figure$\PageIndex{1}$.

Exemple$\PageIndex{1}$: Finding the Interval and Radius of Convergence

Pour chacune des séries suivantes, déterminez l'intervalle et le rayon de convergence.

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$
$\displaystyle \sum_{n=0}^∞n!x^n$
$\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}$

Solution

a. Pour vérifier la convergence, appliquez le test du ratio. Nous avons

\ [\ begin {align*} ρ &= \ lim_ {n→∞} \ gauche| \ dfrac {\ dfrac {x^ {n+1}} {(n+1) !}} {\ dfrac {x^n} {n !}} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} \ gauche| \ dfrac {x^ {n+1}} {(n+1) !} ⋅ \ dfrac {n !} {x^n} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} \ gauche| \ dfrac {x^ {n+1}} {(n+1) ⋅n !} ⋅ \ dfrac {n !} {x^n} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} \ gauche| \ dfrac {x} {n+1} \ droite| \ \ [4 points]
&=|x| \ lim_ {n→∞} \ dfrac {1} {n+1} \ \ [4 points]
&=0<1 \ end {align*} \]

pour toutes les valeurs de$x$. Par conséquent, la série converge pour tous les nombres réels$x$. L'intervalle de convergence est$(−∞,∞)$ et le rayon de convergence est$R=∞.$

b. Appliquez le test du ratio. Car$x≠0$, nous voyons que

\ [\ begin {align*} ρ &= \ lim_ {n→∞} \ gauche| \ dfrac {(n+1) ! x^ {n+1}} {n ! x^n} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} | (n+1) x| \ \ [4 points]
&=|x| \ lim_ {n→∞} (n+1) \ \ [4 points]
&=∞. \ end {align*} \]

Par conséquent, la série diverge pour tous$x≠0$. Comme la série est centrée sur$x=0$, elle doit y converger, de sorte que la série ne converge que pour$x≠0$. L'intervalle de convergence est la valeur unique$x=0$ et le rayon de convergence est$R=0$.

c. Pour appliquer le test du ratio, considérez

\ [\ begin {align*} ρ &= \ lim_ {n→∞} \ gauche| \ dfrac {\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} {\ dfrac {(x−2) ^n} {(n+1) 3^n}} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} \ gauche| \ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} ⋅ \ dfrac {(n+1) 3^n} {(x−2) ^n} \ droite| \ \ [4 points]
&= \ lim_ {n→∞} \ gauche| \ dfrac {(x−2) (n +1)} {3 (n+2)} \ droite| \ \ [4 pt]
&= \ dfrac {|x−2|} {3}. \ end {align*} \]

Le ratio$ρ<1$ de$|x−2|<3$. Cela$|x−2|<3$ implique que$−3<x−2<3,$ la série converge absolument si$−1<x<5$. Le ratio$ρ>1$ de$|x−2|>3$. Par conséquent, la série diverge si$x<−1$ ou$x>5$. Le test du ratio n'est pas concluant si$ρ=1$. Le ratio$ρ=1$ si et seulement si$x=−1$ ou$x=5$. Nous devons tester ces valeurs$x$ séparément. Pour$x=−1$, la série est donnée par

\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]

Comme il s'agit de la série harmonique alternée, elle converge. Ainsi, la série converge vers$x=−1$. Pour$x=5$, la série est donnée par

\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]

Il s'agit de la série harmonique, qui est divergente. Par conséquent, la série de puissance diverge à$x=5$. Nous concluons que l'intervalle de convergence est$[−1,5)$ et que le rayon de convergence est$R=3$.

Exercice$\PageIndex{1}$

Détermine l'intervalle et le rayon de convergence de la série

\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]

Allusion: Appliquez le test du ratio pour vérifier la convergence absolue.

Réponse: L'intervalle de convergence est$[−1,1).$ Le rayon de convergence est$R=1.$

Représenter les fonctions sous forme de séries

Pouvoir représenter une fonction par un « polynôme infini » est un outil puissant. Les fonctions polynomiales sont les fonctions les plus faciles à analyser, car elles n'impliquent que les opérations arithmétiques de base que sont l'addition, la soustraction, la multiplication et la division. Si nous pouvons représenter une fonction complexe par un polynôme infini, nous pouvons utiliser la représentation polynomiale pour la différencier ou l'intégrer. De plus, nous pouvons utiliser une version tronquée de l'expression polynomiale pour approximer les valeurs de la fonction. La question est donc de savoir quand pouvons-nous représenter une fonction par une série de puissances ?

Considérez à nouveau la série géométrique

\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]

Rappelons que la série géométrique

\[a+ar+ar^2+ar^3+\ldots \nonumber \]

converge si et seulement si$|r|<1.$ Dans ce cas, il converge vers$\dfrac{a}{1−r}$. Par conséquent, si$|x|<1$, la série de l'exemple$\PageIndex{1}$ converge vers$\dfrac{1}{1−x}$ et nous écrivons

\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} for|x|<1. \nonumber \]

Par conséquent, nous sommes en mesure de représenter la fonction$f(x)=\dfrac{1}{1−x}$ par la série de puissance

\[1+x+x^2+x^3+\ldots when|x|<1. \nonumber \]

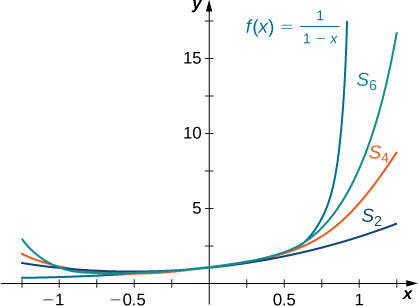
Nous montrons maintenant graphiquement comment cette série fournit une représentation de la fonction$f(x)=\dfrac{1}{1−x}$ en comparant le graphe de$f$ avec les graphes de plusieurs des sommes partielles de cette série infinie.

Exemple$\PageIndex{2}$: Graphing a Function and Partial Sums of its Power Series

Esquissez un graphique$f(x)=\dfrac{1}{1−x}$ et les graphes des sommes partielles correspondantes$ \displaystyle S_N(x)=\sum_{n=0}^Nx^n$ pour$N=2,4,6$ l'intervalle$(−1,1)$. Commentez l'approximation à$S_N$ mesure qu'$N$elle augmente.

Solution

Sur le graphique de la figure, vous voyez qu'à mesure que l'$S_N$on$N$ augmente, on obtient une meilleure approximation$f(x)=\dfrac{1}{1−x}$ pour$x$ l'intervalle$(−1,1)$.

Cette figure est le graphique de y = 1/ (1-x), qui est une courbe croissante avec une asymptote verticale à 1. Sur ce graphique se trouvent également trois sommes partielles de la fonction, S sub 6, S sub 4 et S sub 2. Ces courbes, dans l'ordre, s'aplatissent progressivement. — Figure$\PageIndex{2}$ : Le graphique montre une fonction et trois approximations de celle-ci par des sommes partielles d'une série de puissances.

Exercice$\PageIndex{2}$

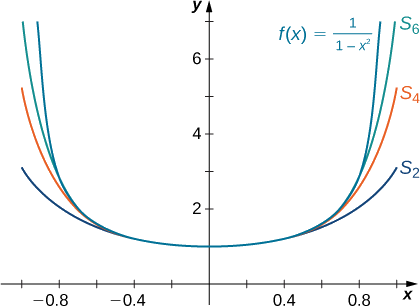
Esquissez un graphique$f(x)=\dfrac{1}{1−x^2}$ et les sommes partielles correspondantes$\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}$ pour$N=2,4,6$ l'intervalle$(−1,1).$

Allusion: $S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}$

Réponse: $Cette figure est le graphique de y = 1/ (1-x^2), qui est une courbe concave vers le haut, symétrique par rapport à l'axe y. Sur ce graphique se trouvent également trois sommes partielles de la fonction, S sub 6, S sub 4 et S sub 2. Ces courbes, dans l'ordre, s'aplatissent progressivement.$

Nous examinons ensuite les fonctions impliquant une expression similaire à la somme d'une série géométrique et montrons comment représenter ces fonctions à l'aide de séries de puissance.

Exemple$\PageIndex{3}$: Representing a Function with a Power Series

Utilisez une série de puissances pour représenter chacune des fonctions suivantes$f$. Déterminez l'intervalle de convergence.

$f(x)=\dfrac{1}{1+x^3}$
$f(x)=\dfrac{x^2}{4−x^2}$

Solution

a. Vous devez reconnaître cette fonction$f$ comme la somme d'une série géométrique, car

\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]

En utilisant le fait que, pour$|r|<1,\dfrac{a}{1−r}$ est la somme des séries géométriques

\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]

nous voyons que, pour$|−x^3|<1,$

\[ \begin{align*} \dfrac{1}{1+x^3} =\dfrac{1}{1−(−x^3)} \\[4pt] =\sum_{n=0}^∞(−x^3)^n \\[4pt] =1−x^3+x^6−x^9+\ldots . \end{align*}\]

Puisque cette série converge si et seulement si$|−x^3|<1$, l'intervalle de convergence est$(−1,1)$, et nous avons

\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots for|x|<1.\nonumber \]

b. Cette fonction n'a pas la forme exacte de la somme d'une série géométrique. Cependant, avec un peu de manipulation algébrique, on peut relier f à une série géométrique. En factorisant 4 des deux termes dans le dénominateur, nous obtenons

\[ \begin{align*} \dfrac{x^2}{4−x^2} =\dfrac{x^2}{4(\dfrac{1−x^2}{4})}\\[4pt] =\dfrac{x^2}{4(1−(\dfrac{x}{2})^2)}.\end{align*}\]

Par conséquent, nous avons

\ [\ begin {align*} \ dfrac {x^2} {4−x^2} &= \ dfrac {x^2} {4 (1− (\ dfrac {x} {2}) ^2)} \ \ [4 points]
&= \ dfrac {\ dfrac {x^2} {4}} {1− (\ dfrac {x} {2}}) ^2} \ \ [4 points]
&= \ sum_ {n=0} ^∞ \ dfrac {x^2} {4} (\ dfrac {x} {2}) ^ {2n}. \ end {align*} \]

La série converge aussi longtemps que$|(\dfrac{x}{2})^2|<1$ (notez que lorsque$|(\dfrac{x}{2})^2|=1$ la série ne converge pas). En résolvant cette inégalité, nous concluons que l'intervalle de convergence est$(−2,2)$ et

\ [\ begin {align*} \ dfrac {x^2} {4−x^2} &= \ sum_ {n=0} ^∞ \ dfrac {x^ {2n+2}} {4^ {n+1}} \ \ [4 points]
&= \ dfrac {x^2} {4} + \ dfrac {x^4} {4^2} + \ dfrac {x^4} ac {x^6} {4^3} + \ ldots \ end {align*} \]

pour$|x|<2.$

Exercice$\PageIndex{3}$

Représentez la fonction$f(x)=\dfrac{x^3}{2−x}$ à l'aide d'une série de puissances et trouvez l'intervalle de convergence.

Allusion: Réécrivez f dans le formulaire$f(x)=\dfrac{g(x)}{1−h(x)}$ pour certaines fonctions$g$ et$h$.

Réponse: $\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}$avec intervalle de convergence$(−2,2)$

Dans les sections suivantes de ce chapitre, nous montrerons comment dériver des représentations de séries de puissances pour de nombreuses autres fonctions, et comment nous pouvons utiliser ces représentations pour évaluer, différencier et intégrer diverses fonctions.

Concepts clés

Pour une série de puissances centrée sur$x=a$, l'une des trois propriétés suivantes est valable :
- i. La série Power ne converge qu'à$x=a$. Dans ce cas, nous disons que le rayon de convergence est$R=0$.
- ii. La série Power converge pour tous les nombres réels$x$. Dans ce cas, nous disons que le rayon de convergence est$R=∞$.
- iii. Il existe un nombre réel R tel que la série converge pour$|x−a|<R$ et diverge pour$|x−a|>R$. Dans ce cas, le rayon de convergence est$R.$
Si une série de puissances converge vers un intervalle fini, la série peut ou non converger aux extrémités.
Le test du ratio peut souvent être utilisé pour déterminer le rayon de convergence.
La série géométrique$\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}$ pour nous$|x|<1$ permet de représenter certaines fonctions à l'aide de séries géométriques.

Équations clés

Série Power centrée sur$x=0$

\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]

Série Power centrée sur$x=a$

\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

Lexique

intervalle de convergence: l'ensemble des nombres réels$x$ pour lesquels une série de puissances converge

série power: une série de la forme$\displaystyle \sum_{n=0}^∞c_nx^n$ est une série de puissances centrée sur$x=0$ ; une série de la forme$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ est une série de puissances centrée sur$x=a$

rayon de convergence: s'il existe un nombre réel$R>0$ tel qu'une série de puissances centrée sur$x=a$ converge pour$|x−a|<R$ et diverge pour$|x−a|>R$, alors$R$ est le rayon de convergence ; si la série de puissances ne converge que vers, le rayon de convergence est ; si la série de puissances converge uniquement vers$x=a$, le rayon de convergence est$R=0$ ; si la série de puissances ne converge converge pour tous les nombres réels$x$, le rayon de convergence est$R=∞$

Définition\(\PageIndex{1}\): Power Series

Remarque\(\PageIndex{1}\): Convergence of a Power Series

Une preuve

Définition : rayon de convergence

Exemple\(\PageIndex{1}\): Finding the Interval and Radius of Convergence

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Graphing a Function and Partial Sums of its Power Series

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Representing a Function with a Power Series

Exercice\(\PageIndex{3}\)