9.4 : Tests de comparaison

Last updated
Save as PDF

Page ID: 197759

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Utilisez le test de comparaison pour tester la convergence d'une série.
Utilisez le test de comparaison des limites pour déterminer la convergence d'une série.

Nous avons vu que le test d'intégrale nous permet de déterminer la convergence ou la divergence d'une série en la comparant à une intégrale impropre associée. Dans cette section, nous montrons comment utiliser des tests de comparaison pour déterminer la convergence ou la divergence d'une série en la comparant à une série dont la convergence ou la divergence est connue. Ces tests sont généralement utilisés pour déterminer la convergence de séries similaires à des séries géométriques ou à des\(p\) séries.

Test de comparaison

Dans les deux sections précédentes, nous avons discuté de deux grandes classes de séries : les séries géométriques et les\(p\) séries. Nous savons exactement quand ces séries convergent et quand elles divergent. Nous montrons ici comment utiliser la convergence ou la divergence de ces séries pour prouver la convergence ou la divergence pour d'autres séries, à l'aide d'une méthode appelée test de comparaison.

Par exemple, considérez la série

\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]

Cette série ressemble à la série convergente

\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]

Comme les termes de chacune des séries sont positifs, la séquence de sommes partielles pour chaque série augmente de manière monotone. En outre, puisque

\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]

pour tous les entiers positifs\(n\), la somme\(k^{\text{th}}\) partielle\(S_k\) de\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) satisfait

\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]

(Voir figure\(\PageIndex{1a}\) et tableau\(\PageIndex{1}\).) Comme la série de droite converge, la séquence\({S_k}\) est bornée au-dessus. Nous concluons qu'\({S_k}\)il s'agit d'une séquence croissante monotone délimitée au-dessus. Par conséquent, selon le théorème de convergence monotone,\({S_k}\) converge, et donc

\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]

converge.

De même, considérez la série

\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]

Cette série ressemble à la série divergente

\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]

La séquence de sommes partielles pour chaque série est monotone croissante et

\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]

pour chaque entier positif\(n\). Par conséquent, la somme\(k^{\text{th}}\) partielle\(S_k\) de

\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]

satisfait

\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]

(Voir figure\(\PageIndex{1n}\) et tableau\(\PageIndex{1}\)). Comme la série\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge à l'infini, la séquence des sommes partielles\(\displaystyle \sum^k_{n=1}\frac{1}{n}\) est illimitée. Par conséquent,\({S_k}\) est une séquence illimitée et diverge donc. Nous concluons que

\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]

diverge.

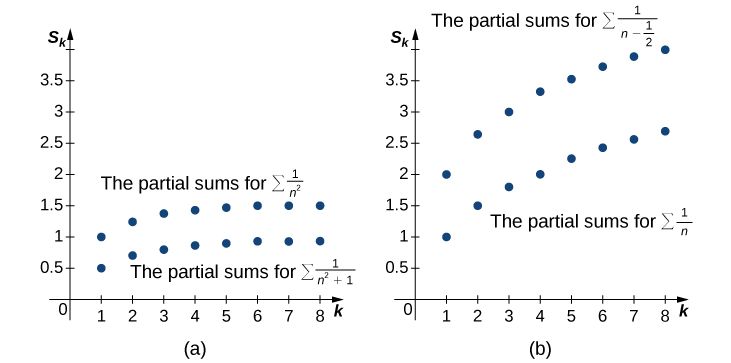
Cela montre deux graphiques côte à côte. La première montre les points tracés pour les sommes partielles de la somme de 1/n^2 et de la somme 1/ (n^2 + 1). Chacune des sommes partielles pour la seconde est inférieure à la somme partielle correspondante pour la première. La seconde montre les points tracés pour les sommes partielles de la somme de 1/ (n - 0,5) et de la somme 1/n. Chacune des sommes partielles pour la seconde est inférieure à la somme partielle correspondante pour la première. — Figure\(\PageIndex{1}\) : (a) Chacune des sommes partielles pour la série donnée est inférieure à la somme partielle correspondante pour la convergence\(p−series\). (b) Chacune des sommes partielles pour la série donnée est supérieure à la somme partielle correspondante pour la série harmonique divergente.

Tableau\(\PageIndex{1}\) : Comparaison d'une série avec une\(p\) série (\(p = 2\))
\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\)	0,5	0,7	0,8	0,8588	0,8973	0,9 243	0,9443	0,9597
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\)	1	1,25	1.3611	1.4236	1,4636	1,4914	1.5118	1 5274

Tableau\(\PageIndex{2}\) : Comparaison d'une série avec la série harmonique
\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\)	2	2.667	3.0667	3.3524	3.5746	3,7564	3.9103	4.0436
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\)	1	1,5	1.833	2.0933	2.2833	2,45	2,5929	2,7 179

Test de comparaison

Supposons qu'il existe un entier\(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
Supposons qu'il existe un entier\(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Une preuve

Nous prouvons la partie i. La preuve de la partie ii. est la preuve contradictoire de la partie i.\({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)

\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]

Par conséquent, la séquence de sommes partielles augmente. En outre, puisque\(a_n≤b_n\) for all \(n≥N\), then

\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]

Par conséquent, pour tous\(k≥1\),

\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]

Depuis\(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.

□

Pour utiliser le test de comparaison afin de déterminer la convergence ou la divergence d'une série\(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.

Exemple\(\PageIndex{1}\): Using the Comparison Test

Pour chacune des séries suivantes, utilisez le test de comparaison afin de déterminer si la série converge ou diverge.

\(\displaystyle \sum_{n=1}^∞=\dfrac{1}{n^3+3n+1}\)
\(\displaystyle \sum_{n=1}^∞=\dfrac{1}{2^n+1}\)
\(\displaystyle \sum_{n=2}^∞=\dfrac{1}{\ln \,n }\)

Solution

a. Comparez à\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Puisque\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) c'est une\(p\) série avec\(p=3\), elle converge. En outre,

\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]

pour chaque entier positif\(n\). Nous pouvons donc en conclure que cela\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) converge.

b. Comparez à\(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Puisque\(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) est une série géométrique avec\(r=\dfrac{1}{2}\) et\(\left|\dfrac{1}{2}\right|<1\), elle converge. En outre,

\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]

pour chaque entier positif\(n\). Nous voyons donc que cela\(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) converge.

c. Comparer à\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Depuis

\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]

pour chaque entier\(n≥2\) et\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) diverge, nous avons ce qui\(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) diverge.

Exercice\(\PageIndex{1}\)

Utilisez le test de comparaison pour déterminer si la série\(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) converge ou diverge.

Allusion: Trouvez une valeur\(p\) telle que\(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).

Réponse: La série converge.

Test de comparaison des limites

Le test de comparaison fonctionne bien si nous pouvons trouver une série comparable satisfaisant à l'hypothèse du test. Cependant, il peut parfois être difficile de trouver une série appropriée. Considérez la série

\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]

Il est naturel de comparer cette série avec la série convergente

\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]

Cependant, cette série ne répond pas à l'hypothèse nécessaire pour utiliser le test de comparaison car

\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]

pour tous les nombres entiers\(n≥2\). Bien que nous puissions rechercher une série différente à comparer, nous montrons\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) plutôt comment utiliser le test de comparaison des limites pour comparer.

\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]

\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Examinons l'idée qui sous-tend le test de comparaison des limites. Considérez deux séries\(\displaystyle \sum^∞_{n=1}a_n\) et\(\displaystyle \sum^∞_{n=1}b_n\)... avec des termes positifs\(a_n\)\(b_n\) et évaluez

\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]

\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]

puis, pour une taille\(n\) suffisamment grande,\(a_n≈Lb_n\). Par conséquent, soit les deux séries convergent, soit les deux séries divergent. Pour la série\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) et\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), on voit que

\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]

Puisque\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) converge, nous concluons que

\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]

converge.

Le test de comparaison des limites peut être utilisé dans deux autres cas. Supposons

\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]

Dans ce cas,\({a_n/b_n}\) est une séquence bornée. Par conséquent, il existe une constante\(M\) telle que\(a_n≤Mb_n\). Par conséquent, si elle\(\displaystyle \sum^∞_{n=1}b_n\) converge, elle\(\displaystyle \sum^∞_{n=1}a_n\) converge. D'un autre côté, supposons

\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]

Dans ce cas,\({a_n/b_n}\) est une séquence illimitée. Par conséquent, pour chaque constante,\(M\) il existe un entier\(N\) tel que\(a_n≥Mb_n\) pour toutes.\(n≥N.\) Par conséquent, si\(\displaystyle \sum^∞_{n=1}b_n\) diverge, alors\(\displaystyle \sum^∞_{n=1}a_n\) diverge également.

Test de comparaison des limites

Laissez-le\(a_n,b_n≥0\) pour tous\(n≥1.\)

Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) alors\(\displaystyle \sum^∞_{n=1}a_n\) et\(\displaystyle \sum^∞_{n=1}b_n\) les deux convergent ou si les deux divergent.
Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) et\(\displaystyle \sum^∞_{n=1}b_n\) converge, alors\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Si\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) et\(\displaystyle \sum^∞_{n=1}b_n\) diverge, alors\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

Notez que si\(\dfrac{a_n}{b_n}→0\) et\(\displaystyle \sum^∞_{n=1}b_n\) divergent, le test de comparaison des limites ne donne aucune information. De même, si\(\dfrac{a_n}{b_n}→∞\) et\(\displaystyle \sum^∞_{n=1}b_n\) converge, le test ne fournit également aucune information. Par exemple, considérez les deux séries\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) et\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Ces séries sont toutes deux des\(p\) séries avec\(p=\frac{1}{2}\) et\(p=2\), respectivement. Puisque\(p=\frac{1}{2}<1,\) la série\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) diverge. En revanche, depuis\(p=2>1\), la série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converge. Supposons toutefois que nous ayons essayé d'appliquer le test de comparaison des limites, en utilisant la \(p\)série convergente −series\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) comme série de comparaison. Tout d'abord, nous voyons que

\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]

De même, nous constatons que

\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]

Par conséquent, si\(\dfrac{a_n}{b_n}→∞\) lors de\(\displaystyle \sum_{n=1}^∞b_n\) la convergence, nous n'obtenons aucune information sur la convergence ou la divergence de\(\displaystyle \sum_{n=1}^∞a_n\).

Exemple\(\PageIndex{2}\): Using the Limit Comparison Test

Pour chacune des séries suivantes, utilisez le test de comparaison des limites afin de déterminer si la série converge ou diverge. Si le test ne s'applique pas, dites-le.

\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
\(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)

Solution

a. Comparez cette série à\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Calculer

\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)

Selon le test de comparaison des limites, puisque\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) diverge, puis\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) diverge.

b. Comparez cette série à\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). Nous voyons que

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)

Par conséquent,

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)

Puisque\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) converge, nous en concluons que cela\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) converge.

c. Depuis,\(\ln n<n,\) comparez avec\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). Nous voyons que

\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)

Pour évaluer\(\displaystyle \lim_{n→∞}\ln n/n\), évaluez la limite en fonction\(x→∞\) de la fonction à valeur réelle\(\ln(x)/x\). Ces deux limites sont égales, et cette modification nous permet d'utiliser la règle de L'Hôpital. Nous obtenons

\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)

Par conséquent\(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), et par conséquent,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)

Comme la limite est\(0\)\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) divergente, le test de comparaison des limites ne fournit aucune information.

Comparez\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) plutôt avec. Dans ce cas,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)

Comme la limite\(∞\) n'est que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) convergente, le test ne fournit toujours aucune information.

Alors maintenant, nous essayons une série entre les deux que nous avons déjà essayés. En choisissant la série\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), on constate que

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).

Comme ci-dessus, pour évaluer\(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), évaluez la limite à partir\(x→∞\) de la fonction à valeur réelle\(\frac{\ln n}{\sqrt{n}}\). Selon la règle de L'Hôpital,

\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).

Puisque la limite est\(0\) et\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) converge, nous pouvons en conclure que cela\(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) converge.

Exercice\(\PageIndex{2}\)

Utilisez le test de comparaison des limites pour déterminer si la série\(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) converge ou diverge.

Allusion: Comparez avec une série géométrique.

Réponse: La série diverge.

Concepts clés

Les tests de comparaison sont utilisés pour déterminer la convergence ou la divergence des séries avec des termes positifs.
Lors de l'utilisation des tests de comparaison, une série\(\displaystyle \sum^∞_{n=1}a_n\) est souvent comparée à une\(p\) série géométrique.

Lexique

test de comparaison: Si\(0≤a_n≤b_n\) pour tous\(n≥N\) et\(\displaystyle \sum^∞_{n=1}b_n\) converge, alors\(\displaystyle \sum^∞_{n=1}a_n\) converge ; si\(a_n≥b_n≥0\) pour tous\(n≥N\) et\(\displaystyle \sum^∞_{n=1}b_n\) diverge, alors\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

test de comparaison des limites: Supposons\(a_n,b_n≥0\) pour tous\(n≥1\). Si\(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), alors\(\displaystyle \sum^∞_{n=1}a_n\) et\(\displaystyle \sum^∞_{n=1}b_n\) les deux convergent ou les deux divergent ; si\(\displaystyle \lim_{n→∞}a_n/b_n→0\) et\(\displaystyle \sum^∞_{n=1}b_n\) convergent, alors\(\displaystyle \sum^∞_{n=1}a_n\) convergent. Si\(\displaystyle \lim_{n→∞}a_n/b_n→∞\) et\(\displaystyle \sum^∞_{n=1}b_n\) diverge, alors\(\displaystyle \sum^∞_{n=1}a_n\) diverge.