8.6 : Exercices de révision du chapitre 8

Last updated
Save as PDF

Page ID: 197433

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vrai ou faux ? Justifiez votre réponse par une preuve ou un contre-exemple.

1) L'équation différentielle$y'=3x^2y−\cos(x)y''$ est linéaire.

2) L'équation différentielle$y'=x−y$ est séparable.

Réponse: $F$

3) Vous pouvez résoudre explicitement toutes les équations différentielles du premier ordre par séparation ou par la méthode d'intégration des facteurs.

4) Vous pouvez déterminer le comportement de toutes les équations différentielles du premier ordre à l'aide de champs directionnels ou de la méthode d'Euler.

Réponse: $T$

Pour les problèmes suivants, trouvez la solution générale aux équations différentielles.

5)$y′=x^2+3e^x−2x$

6)$y'=2^x+\cos^{−1}x$

Réponse: $y(x)=\frac{2^x}{ln(2)}+xcos^{−1}x−\sqrt{1−x^2}+C$

7)$y'=y(x^2+1)$

8)$y'=e^{−y}\sin x$

Réponse: $y(x)=\ln(C−\cos x)$

9)$y'=3x−2y$

10)$y'=y\ln y$

Réponse: $y(x)=e^{e^{C+x}}$

Pour les problèmes suivants, trouvez la solution au problème de valeur initiale.

11)$y'=8x−\ln x−3x^4, \quad y(1)=5$

(12)$y'=3x−\cos x+2, \quad y(0)=4$

Réponse: $y(x)=4+\frac{3}{2}x^2+2x−\sin x$

13)$xy'=y(x−2), \quad y(1)=3$

(14)$y'=3y^2(x+\cos x), \quad y(0)=−2$

Réponse: $y(x)=−\dfrac{2}{1+3(x^2+2\sin x)}$

15)$(x−1)y'=y−2, \quad y(0)=0$

16)$y'=3y−x+6x^2, \quad y(0)=−1$

Réponse: $y(x)=−2x^2−2x−\frac{1}{3}−\frac{2}{3}e^{3x}$

Pour les problèmes suivants, dessinez le champ directionnel associé à l'équation différentielle, puis résolvez l'équation différentielle. Dessinez un échantillon de solution sur le champ directionnel.

17)$y'=2y−y^2$

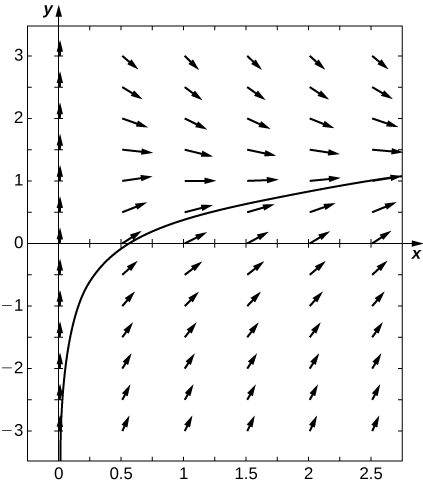
18)$y'=\dfrac{1}{x}+\ln x−y,$ pour$x>0$

Réponse

$y(x)=Ce^{−x}+\ln x$

$Champ de direction avec des flèches pointant vers le haut et vers la droite le long d'une courbe logarithmique qui se rapproche de l'infini négatif lorsque x passe à zéro et augmente lorsque x passe à l'infini.$

Pour les problèmes suivants, utilisez la méthode d'Euler avec des$n=5$ étapes sur l'intervalle. Résolvez$t=[0,1].$ ensuite exactement le problème de la valeur initiale. Dans quelle mesure se situe votre estimation selon la méthode d'Euler ?

19)$y'=−4yx, \quad y(0)=1$

(20)$y'=3^x−2y, \quad y(0)=0$

Réponse: Euler :$0.6939$, Solution
exacte :$y(x)=\dfrac{3^x−e^{−2x}}{2+\ln(3)}$

Pour les problèmes suivants, configurez et résolvez les équations différentielles.

21) Une voiture roule le long d'une autoroute, accélérant selon$a=5\sin(πt),$ où$t$ représente le temps en minutes. Trouvez la vitesse à tout moment$t$, en supposant que la voiture démarre à une vitesse initiale de$60$ mi/h.

22) Vous lancez une balle de$2$ kilogrammes de masse en l'air avec une vitesse ascendante de$8$ m/s. Trouvez exactement le temps pendant lequel la balle restera en l'air, en supposant que la gravité est donnée par$g=9.8\,\text{m/s}^2$.

Réponse: $\frac{40}{49}$seconde

23) Vous lâchez une balle d'une masse de$5$ kilogrammes par la fenêtre d'un avion à une hauteur de$5000$ m. Combien de temps faut-il pour que la balle atteigne le sol ?

24) Vous lâchez la même balle de$5$ kilogrammes de masse par la même fenêtre d'avion à la même hauteur, sauf que cette fois, vous supposez une force de traînée proportionnelle à la vitesse de la balle, en utilisant une constante de proportionnalité de$3$ et la balle atteint sa vitesse terminale. Résolvez la distance parcourue en fonction du temps. Combien de temps faut-il au ballon pour atteindre le sol ?

Réponse: $x(t)=5000+\frac{245}{9}−\frac{49}{3}t−\frac{245}{9}e^{−5/3t}, \quad t=307.8$secondes

25) Un médicament est administré à un patient toutes les$24$ heures et est éliminé à un rythme proportionnel à la quantité de médicament restant dans le corps, avec une proportionnalité constante$0.2$. Si le patient a besoin d'un taux de base de$5$ mg pour être présent dans le sang à tout moment, quelle doit être la dose ?

26) Un réservoir$1000$ d'un litre contient de l'eau pure et une solution de$0.2$ kg de sel/L est pompée dans le réservoir à un débit de$1$ L/min et est drainée au même débit. Résolvez pour obtenir la quantité totale de sel dans le réservoir à la fois$t$.

Réponse: $T(t)=200\left(1−e^{−t/1000}\right)$

27) Vous faites bouillir de l'eau pour faire du thé. Lorsque vous versez l'eau dans votre théière, la température est.$100°C.$ Après$5$ quelques minutes passées dans votre$15°C$ chambre, la température du thé est$85°C$. Résolvez l'équation pour déterminer la température du thé à un moment donné$t$. Combien de temps devez-vous attendre jusqu'à ce que le thé soit à une température buvable ($72°C$) ?

28) La population humaine (en milliers) du Nevada en$1950$ était d'environ$160$. Si la capacité de charge est estimée à un$10$ million d'individus et en supposant un$2\%$ taux de croissance annuel, développez un modèle de croissance logistique et résolvez pour la population du Nevada à tout moment (utilisez$1950$ comme temps = 0). Pour quelle population votre modèle prévoit-il$2000$ ? Dans quelle mesure votre prédiction se rapproche-t-elle de la valeur réelle de$1,998,257$ ?

Réponse: $P(t)=\dfrac{1600000e^{0.02t}}{9840+160e^{0.02t}}$

29) Répétez le problème précédent mais utilisez le modèle de croissance de Gompertz. Qu'est-ce qui est le plus précis ?