Skip to main content
Global

8.4E : Exercices pour la section 8.4

  1. Last updated
  2. Save as PDF
  • Page ID
    197421

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Modèle logistique de base

    Pour les problèmes 1 à 11, considérez l'équation logistique sous la forme\( P'=CP−P^2.\) Dessiner le champ directionnel et trouvez la stabilité des équilibres.

    1)\( C=3\)

    2)\( C=0\)

    Réponse

    \( P=0\)semi-stable

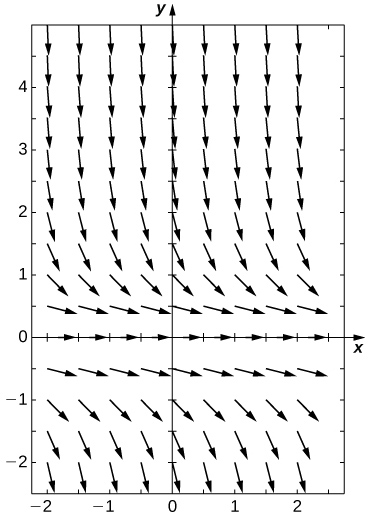
    3)\( C=−3\)

    4) Résolvez l'équation logistique\( C=10\) et une condition initiale de\( P(0)=2.\)

    Réponse
    \( P=\dfrac{10e^{10x}}{e^{10x}+4}\)

    5) Résolvez l'équation logistique\( C=−10\) et une condition initiale de\( P(0)=2\).

    6) Une population de cerfs à l'intérieur d'un parc a une capacité de charge\( 200\) et un taux de croissance de\( 2%\). Si la population initiale est constituée de\( 50\) cerfs, quelle est la population de cerfs à un moment donné ?

    Réponse
    \( P(t)=\dfrac{10000e^{0.02t}}{150+50e^{0.02t}}\)

    7) Une population de grenouilles dans un étang a un taux de croissance de\( 5%.\) Si la population initiale est constituée de\( 1000\) grenouilles et que la capacité de charge est\( 6000\), quelle est la population de grenouilles à un moment donné ?

    8) [T] Les bactéries se développent à un rythme\( 20%\) horaire dans une boîte de Pétri. S'il existe initialement une bactérie et une capacité de charge de\( 1\) millions de cellules, combien de temps faut-il pour atteindre\( 500,000\) les cellules ?

    Réponse
    \( 69\)heures\( 5\) minutes

    9) [T] Les lapins d'un parc ont une population initiale de\( 10\) et croissent à un rythme\( 4%\) annuel. Si la capacité de charge est de\( 500\), à quelle heure la population atteint-elle les\( 100\) lapins ?

    10) [T] Deux singes sont placés sur une île. Après des\( 5\) années, il y a\( 8\) des singes et la capacité de charge estimée est celle des\( 25\) singes. Quand la population de singes atteint-elle les\( 16\) singes ?

    Réponse
    \( 8\)années\( 11\) mois

    11) [T] Un sanctuaire de papillons est construit pour accueillir des\( 2000\) papillons, et les\( 400\) papillons sont initialement emménagés. Si après des\( 2\) mois il y a maintenant\( 800\) des papillons, quand est-ce que la population atteindra\( 1500\) les papillons ?

    Modèle logistique de population avec épuisement

    Les problèmes suivants examinent l'équation logistique en ajoutant un terme désignant l'épuisement, que ce soit par décès ou par émigration.

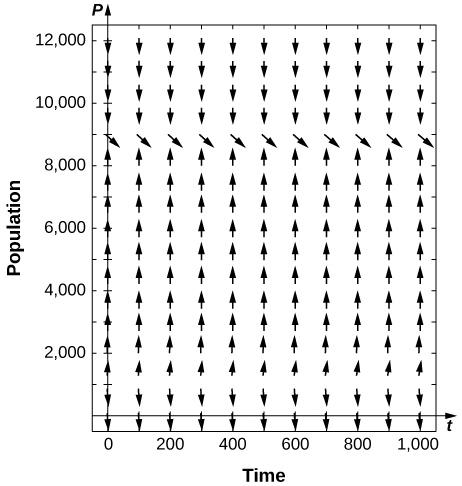
    12) [T] La population de truites dans un étang est donnée par\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−400\), où les\( 400\) truites sont capturées chaque année. Utilisez votre calculatrice ou un logiciel informatique pour dessiner un champ directionnel et dessiner quelques exemples de solutions. Qu'attendez-vous de ce comportement ?

    Réponse

    13) Dans le problème précédent, quelles sont les stabilités des équilibres\( 0<P_1<P_2\) ?

    14) [T] Pour le problème précédent, utilisez un logiciel pour générer un champ directionnel pour la valeur\( f=400\). Quelles sont les stabilités des équilibres ?

    Réponse

    \( P_1\)semi-stable

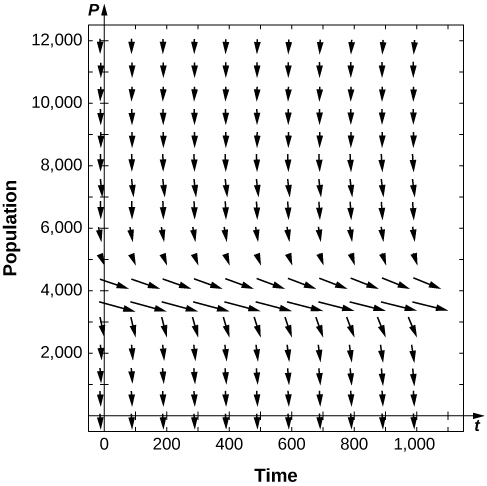
    15) [T] Pour les problèmes précédents, utilisez un logiciel pour générer un champ directionnel pour la valeur\( f=600.\) Quelles sont les stabilités des équilibres ?

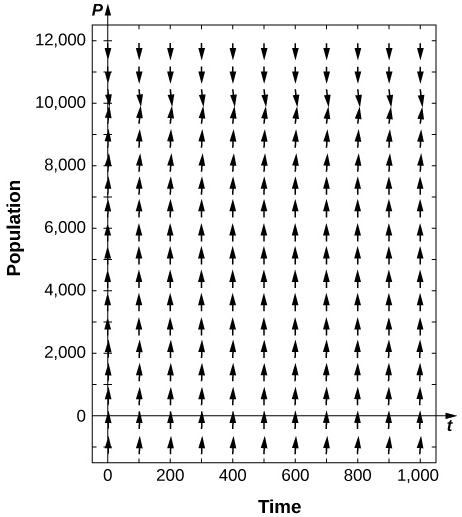
    16) [T] Pour les problèmes précédents, considérez le cas où un certain nombre de poissons sont ajoutés à l'étang, ou\( f=−200.\) Quels sont les équilibres non négatifs et leur stabilité ?

    Réponse

    \( P_2>0\)étable

    Il est plus probable que la quantité de pêche soit régie par le nombre actuel de poissons présents. Ainsi, au lieu d'un nombre constant de poissons capturés, le taux est proportionnel au nombre actuel de poissons présents, avec une proportionnalité constante\( k\), comme\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−kP.\)

    17) [T] Pour le problème de pêche précédent, dessinez un champ directionnel en supposant\( k=0.1\). Dessinez des solutions qui présentent ce comportement. Quels sont les équilibres et quelles sont leurs stabilités ?

    18) [T] Utilisez un logiciel ou une calculatrice pour dessiner des champs directionnels pour\( k=0.4\). Quels sont les équilibres non négatifs et leur stabilité ?

    Réponse

    \( P_1=0\)est semi-stable

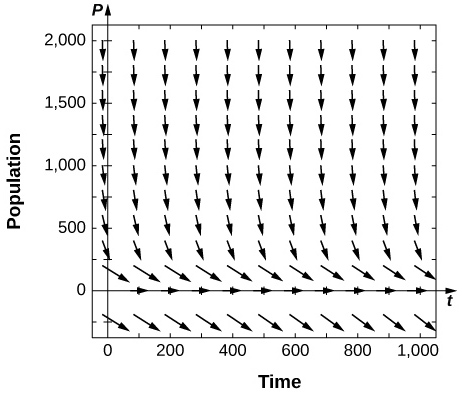
    19) [T] Utilisez un logiciel ou une calculatrice pour dessiner des champs directionnels pour\( k=0.6\). Quels sont les équilibres et leur stabilité ?

    20) Résolvez cette équation en supposant une valeur\( k=0.05\) et un état initial du\( 2000\) poisson.

    Réponse
    \( y=\dfrac{−20}{4×10^{−6}−0.002e^{0.01t}}\)

    21) Résolvez cette équation en supposant une valeur\( k=0.05\) et un état initial du\( 5000\) poisson.

    Seuils minimaux de population durable

    Les problèmes suivants ajoutent une valeur seuil minimale pour la survie de l'espèce\( T\), ce qui modifie l'équation différentielle en\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\).

    22) Dessinez le champ directionnel de l'équation logistique du seuil, en supposant\( K=10,r=0.1,T=2\). Quand est-ce que la population survivra ? Quand disparaît-il ?

    Réponse

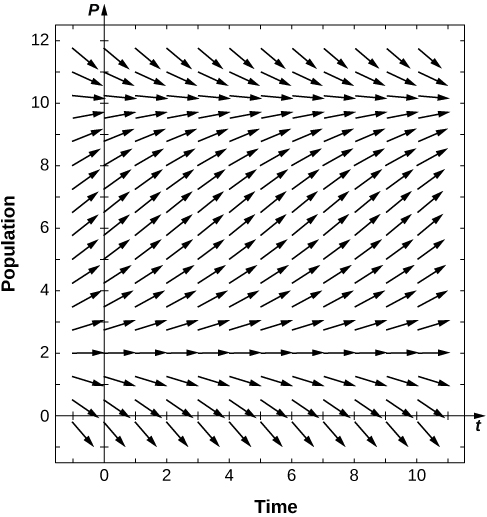
    23) Pour le problème précédent, résolvez l'équation du seuil logistique en supposant la condition initiale\( P(0)=P_0\).

    24) Les tigres du Bengale vivant dans un parc de conservation ont une capacité de charge\( 100\) et ont besoin d'un minimum\( 10\) pour survivre. Si leur population augmente à un rythme\( 1%\) annuel, avec une population initiale de\( 15\) tigres, déterminez le nombre de tigres présents.

    Réponse
    \( P(t)=\dfrac{850+500e^{0.009t}}{85+5e^{0.009t}}\)

    25) Une forêt contenant des lémuriens à queue annelée à Madagascar a le potentiel de soutenir\( 5000\) des individus, et la population de\( 5%\) lémuriens augmente à un rythme annuel. Un minimum de 500 individus est nécessaire à la survie des lémuriens. Étant donné une population initiale de\( 600\) lémuriens, déterminez la population de lémuriens.

    26) La population de lions de montagne dans le nord de l'Arizona a une capacité de charge estimée à\( 250\) et augmente à un rythme\( 0.25%\) annuel, et il doit y en avoir\( 25\) pour que la population survive. Avec une population initiale de lions de\( 30\) montagne, combien d'années faudra-t-il pour que les lions de montagne soient retirés de la liste des espèces menacées (au moins\( 100\)) ?

    Réponse
    \( 13\)années mois

    L'équation de Gompertz

    Les questions suivantes portent sur l'équation de Gompertz, une modification de la croissance logistique, qui est souvent utilisée pour modéliser la croissance du cancer, en particulier le nombre de cellules tumorales.

    (27) L'équation de Gompertz est donnée par\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t).\) Dessiner les champs directionnels pour cette équation en supposant que tous les paramètres sont positifs, et étant donné que\( K=1.\)

    28) Supposons que pour une population,\( K=1000\) et\( α=0.05\). Dessinez le champ directionnel associé à cette équation différentielle et tracez quelques solutions. Quel est le comportement de la population ?

    Réponse

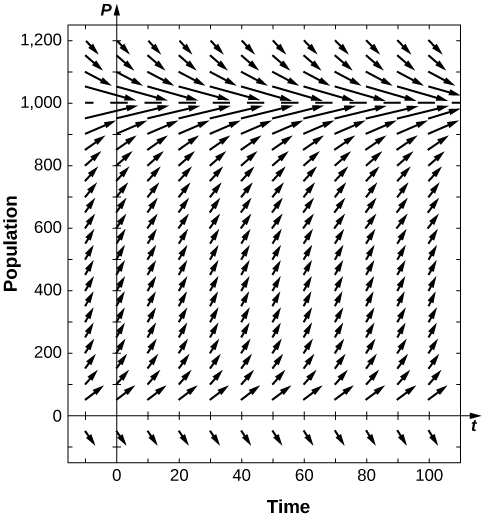
    29) Résolvez l'équation de Gompertz pour les génériques\( α\)\( K\) et\( P(0)=P_0\).

    30) [T] L'équation de Gompertz a été utilisée pour modéliser la croissance tumorale dans le corps humain. En partant d'une cellule tumorale par jour\( 1\)\( α=0.1\) et en supposant une capacité de charge de\( 10\) millions de cellules, combien de temps faut-il pour atteindre le stade de « détection » d'un\( 5\) million de cellules ?

    Réponse
    \( 31.465\)jours

    31) [T] On estime que la population humaine mondiale a atteint des\( 3\) milliards de personnes\( 1959\) et des\( 6\) milliards de personnes\( 1999\). En supposant une capacité de charge d'un\( 16\) milliard d'humains, écrivez et résolvez l'équation différentielle de la croissance logistique, et déterminez en quelle année la population a atteint le\( 7\) milliard.

    32) [T] On estime que la population humaine mondiale a atteint des\( 3\) milliards de personnes\( 1959\) et des\( 6\) milliards de personnes\( 1999\). En supposant une capacité de charge d'un\( 16\) milliard d'humains, écrivez et résolvez l'équation différentielle de la croissance de Gompertz, et déterminez en quelle année la population a atteint le\( 7\) milliard. La croissance logistique ou la croissance de Gompertz était-elle plus précise, étant donné que la population mondiale a atteint des\( 7\) milliards de personnes en octobre\( 31,2011?\)

    Réponse
    septembre\( 2008\)

    33) Montrez que la population croît le plus rapidement lorsqu'elle atteint la moitié de la capacité de charge de l'équation logistique\( P'=rP\left(1−\dfrac{P}{K}\right)\).

    34) Quand la population augmente-t-elle le plus rapidement dans l'équation logistique du seuil\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\) ?

    Réponse
    \( \dfrac{K+T}{2}\)

    35) Quand la population augmente-t-elle le plus rapidement selon l'équation de Gompertz ?\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t)?\)

    Vous trouverez ci-dessous un tableau des populations de grues blanches à l'état sauvage de\( 1940\) à\( 2000\). La population a rebondi après avoir failli disparaître après le début des efforts de conservation. Les problèmes suivants concernent l'application de modèles de population pour ajuster les données. Supposons la capacité de charge des\( 10,000\) grues. Ajustez les données en supposant que les années se sont écoulées depuis\( 1940\) (de sorte que votre population initiale\( 0\) soit\( 22\) composée de grues).

    Année (années depuis le début de la conservation) Population de grues blanches
    1940 (0) 22
    1950 (10) 31
    1960 (20) 36
    1970 (30) 57
    1980 (40) 91
    1990 (50) 159
    2000 (60) 256

    Une source : https://www.savingcranes.org/images/...wc_numbers.pdf

    36) Trouvez l'équation et le paramètre\( r\) qui correspondent le mieux aux données de l'équation logistique.

    Réponse
    \( r=0.0405\)

    37) Trouvez l'équation\( r\) et les paramètres\( T\) qui correspondent le mieux aux données de l'équation logistique du seuil.

    38) Trouvez l'équation et le paramètre\( α\) qui correspondent le mieux aux données de l'équation de Gompertz.

    Réponse
    \( α=0.0081\)

    39) Représenter graphiquement les trois solutions et les données sur le même graphique. Quel modèle semble le plus précis ?

    40) À l'aide des trois équations trouvées dans les problèmes précédents, estimez la population en\( 2010\) (année\( 70\) après la conservation). La population réelle mesurée à cette époque était de\( 437\). Quel modèle est le plus précis ?

    Réponse
    Logistique :\( 361\), Seuil :\( 436\), Gompertz :\( 309\).