8.5 : Équations linéaires du premier ordre

Objectifs d'apprentissage

• Écrivez une équation différentielle linéaire du premier ordre sous forme standard.
• Trouvez un facteur d'intégration et utilisez-le pour résoudre une équation différentielle linéaire du premier ordre.
• Résolvez des problèmes appliqués impliquant des équations différentielles linéaires de premier ordre

Plus tôt, nous avons étudié l'application d'une équation différentielle du premier ordre qui impliquait de résoudre la vitesse d'un objet. En particulier, si une balle est lancée vers le haut avec une vitesse initiale de\( v_0\) pieds/s, alors un problème de valeur initiale qui décrit la vitesse de la balle après\( t\) quelques secondes est donné par

\[ \dfrac{dv}{dt}=−32 \nonumber \]

avec\(v(0)=v_0.\)

Ce modèle suppose que la seule force agissant sur la balle est la gravité. Nous ajoutons maintenant au problème en tenant compte de la possibilité que la résistance de l'air agisse sur le ballon.

La résistance à l'air agit toujours dans la direction opposée au mouvement. Par conséquent, si un objet s'élève, la résistance de l'air agit vers le bas. Si l'objet tombe, la résistance à l'air agit vers le haut (Figure\( \PageIndex{1}\)). Il n'existe pas de relation exacte entre la vitesse d'un objet et la résistance de l'air agissant sur celui-ci. Pour les très petits objets, la résistance de l'air est proportionnelle à la vitesse ; c'est-à-dire que la force due à la résistance de l'air est numériquement égale à certains\( k\) temps constants\( v\). Pour les objets plus grands (par exemple, de la taille d'une balle de baseball), selon leur forme, la résistance à l'air peut être approximativement proportionnelle au carré de la vitesse. En fait, la résistance de l'air peut être proportionnelle à\( v^{1.5}\), ou\( v^{0.9}\), ou à une autre puissance de\( v\).

Figure\( \PageIndex{1}\) : Forces agissant sur une balle de baseball en mouvement : la gravité agit vers le bas et la résistance de l'air agit dans une direction opposée à la direction du mouvement.

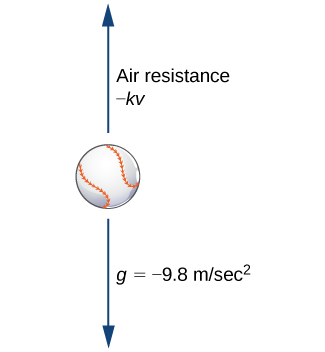
Nous travaillerons avec l'approximation linéaire de la résistance à l'air. Si nous supposons\( k>0\), alors l'expression de la force\( F_A\) due à la résistance de l'air est donnée par\( FA_=−kv\). La somme des forces agissant sur l'objet est donc égale à la somme de la force gravitationnelle et de la force due à la résistance de l'air. Ceci, à son tour, est égal à la masse de l'objet multipliée par son accélération dans le temps\( t\) (deuxième loi de Newton). Cela nous donne l'équation différentielle

\[ m\dfrac{dv}{dt}=−kv−mg. \nonumber \]

Enfin, nous imposons une condition initiale\( v(0)=v_0,\) où\( v_0\) est la vitesse initiale mesurée en mètres par seconde. Cela fait\( g=9.8m/s^2.\) que le problème de la valeur initiale devient

\[ m\dfrac{dv}{dt}=−kv−mg \nonumber \]

avec\(v(0)=v_0.\)

L'équation différentielle de ce problème de valeur initiale est un exemple d'équation différentielle linéaire du premier ordre. (Rappelez-vous qu'une équation différentielle est du premier ordre si la dérivée d'ordre le plus élevé qui apparaît dans l'équation l'est\( 1\).) Dans cette section, nous étudions des équations linéaires de premier ordre et examinons une méthode permettant de trouver une solution générale à ces types d'équations, ainsi que de résoudre les problèmes de valeur initiale les impliquant.

Définition : Équation différentielle linéaire du premier ordre

Une équation différentielle du premier ordre est linéaire si elle peut être écrite sous la forme

\[a(x)y′+b(x)y=c(x), \nonumber \]

où\( a(x),b(x),\) et\( c(x)\) sont des fonctions arbitraires de\( x\).

N'oubliez pas que la fonction inconnue\( y\) dépend de la variable\( x\), c'est-à-dire qu'elle\( x\) est la variable indépendante et\( y\) la variable dépendante. Voici quelques exemples d'équations différentielles linéaires du premier ordre :

\[ (3x^2−4)y'+(x−3)y=\sin x \nonumber \]

\[ (\sin x)y'−(\cos x)y=\cot x \nonumber \]

\[ 4xy'+(3\ln x)y=x^3−4x. \nonumber \]

Voici des exemples d'équations différentielles non linéaires de premier ordre :

\[ (y')^4−(y')^3=(3x−2)(y+4) \nonumber \]

\[ 4y'+3y^3=4x−5 \nonumber \]

\[(y')^2=\sin y+\cos x. \nonumber \]

Ces équations ne sont pas linéaires à cause de termes tels que\( (y′)^4,y^3,\) etc. À cause de ces termes, il est impossible de mettre ces équations sous la même forme que l'équation.

Formulaire standard

Considérez l'équation différentielle

\[ (3x^2−4)y′+(x−3)y=\sin x. \nonumber \]

Notre objectif principal dans cette section est de dériver une méthode de solution pour les équations de cette forme. Il est utile que le coefficient\( y′\) soit égal à\( 1\). Pour que cela se produise, nous divisons les deux côtés par\( 3x^2−4.\)

\[ y′+ \left(\dfrac{x−3}{3x^2−4} \right)y=\dfrac{\sin x}{3x^2−4} \nonumber \]

C'est ce que l'on appelle la forme standard de l'équation différentielle. Nous l'utiliserons plus tard pour trouver la solution à une équation différentielle linéaire générale du premier ordre. Pour en revenir à l'équation, nous pouvons diviser les deux côtés de l'équation par\( a(x)\). Cela conduit à l'équation

\[ y′+\dfrac{b(x)}{a(x)}y=\dfrac{c(x)}{a(x)}. \label{eq5} \]

Définissez maintenant

\[ p(x)=\dfrac{b(x)}{a(x)} \nonumber \]

et

\[ q(x)=\dfrac{c(x)}{a(x)} \nonumber \]

Ensuite, l'équation \ ref {eq5} devient

\[ y′+p(x)y=q(x). \nonumber \]

Nous pouvons écrire n'importe quelle équation différentielle linéaire du premier ordre sous cette forme, appelée forme standard pour une équation différentielle linéaire du premier ordre.

Exemple\( \PageIndex{1}\): Writing First-Order Linear Equations in Standard Form

Mettez chacune des équations différentielles linéaires du premier ordre suivantes sous forme standard. Identifiez\( p(x)\) et\( q(x)\) pour chaque équation.

1. \( y'=3x−4y\)
2. \( \dfrac{3xy'}{4y−3}=2\)(ici\( x>0\))
3. \( y=3y'−4x^2+5\)

Solution

a. Ajouter\( 4y\) sur les deux côtés :

\( y'+4y=3x.\)

Dans cette équation,\( p(x)=4\) et \ | (q (x) =3x. \)

b. Multipliez les deux côtés par\( 4y−3\), puis soustrayez\( 8y\) de chaque côté :

\( \dfrac{3xy'}{4y−3}=2\)

\( 3xy'=2(4y−3)\)

\( 3xy'=8y−6\)

\( 3xy'−8y=−6.\)

Enfin, divisez les deux côtés par\( 3x\) pour que le coefficient soit\( y'\) égal à\( 1\) :

\( y'−\dfrac{8}{3x}y=−\dfrac{2}{3x}.\)

Cela est permis car dans l'exposé initial de ce problème, nous l'avons supposé\( x>0\). (Si\( x=0\) alors l'équation d'origine devient\( 0=2\), ce qui est clairement une fausse déclaration.)

Dans cette équation,\( p(x)=−\dfrac{8}{3x}\) et\( q(x)=−\dfrac{2}{3x}\).

c. Soustraire\( y\) de chaque côté et ajouter\( 4x^2−5\) :

\( 3y'−y=4x^2−5.\)

Divisez ensuite les deux côtés par\( 3\) :

\( y'−\dfrac{1}{3}y=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Dans cette équation,\( p(x)=−\dfrac{1}{3}\) et\( q(x)=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Exercice\(\PageIndex{1}\)

Mettez l'\( \dfrac{(x+3)y'}{2x−3y−4}=5\)équation sous forme standard et identifiez\( p(x)\) et\( q(x)\).

Allusion

Multipliez les deux côtés par le dénominateur commun, puis collectez tous les termes impliquant d'un\( y\) côté.

Réponse

\[ y'+\dfrac{15}{x+3}y=\dfrac{10x−20}{x+3} \nonumber \]

\[p(x)=\dfrac{15}{x+3} \nonumber \]

et

\[ q(x)=\dfrac{10x−20}{x+3} \nonumber \]

Facteurs d'intégration

Nous développons maintenant une technique de solution pour toute équation différentielle linéaire de premier ordre. Nous commençons par la forme standard d'une équation différentielle linéaire du premier ordre :

\[ y'+p(x)y=q(x). \label{Deq1} \]

Le premier terme sur le côté gauche de l'équation est la dérivée de la fonction inconnue, et le second terme est le produit d'une fonction connue avec la fonction inconnue. Cela rappelle quelque peu la règle du pouvoir. Si nous multiplions l'équation \ ref {Deq1} par une fonction qui n'a pas encore été déterminée\( μ(x)\), alors l'équation devient

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq2} \]

L'équation de gauche \ ref {Deq2} peut être parfaitement adaptée à la règle du produit :

\[ \dfrac{d}{dx}[f(x)g(x)]=f′(x)g(x)+f(x)g′(x). \nonumber \]

Faire correspondre terme par terme donne\( y=f(x),g(x)=μ(x)\), et\( g′(x)=μ(x)p(x)\). Prendre la dérivée de\( g(x)=μ(x)\) et la mettre comme égale à la partie droite de\( g′(x)=μ(x)p(x)\) conduit à

\[ μ′(x)=μ(x)p(x). \nonumber \]

Il s'agit d'une équation différentielle séparable de premier ordre pour\(μ(x).\) Nous le savons\( p(x)\) parce qu'elle apparaît dans l'équation différentielle que nous résolvons. Séparer les variables et intégrer les rendements

\[ \begin{align} \dfrac{μ′(x)}{μ(x)} =p(x) \\[4pt] ∫\dfrac{μ′(x)}{μ(x)}dx =∫p(x)dx \\[4pt] \ln|μ(x)| =∫p(x)dx+C \\[4pt] e^{\ln|μ(x)|} =e^{∫p(x)dx+C} \\[4pt] |μ(x)| =C_1e^{∫p(x)dx} \\[4pt] μ(x) =C_2e^{∫p(x)dx}. \end{align} \nonumber \]

Il\( C_2\) peut s'agir d'une constante arbitraire (positive ou négative). Cela conduit à une méthode générale pour résoudre une équation différentielle linéaire du premier ordre. Nous multiplions d'abord les deux côtés de l'équation par le facteur d'intégration,\( μ(x).\) ce qui donne

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq5} \]

Le côté gauche de l'équation \ ref {Deq5} peut être réécrit comme suit\( \dfrac{d}{dx}(μ(x)y)\) :

\[ \dfrac{d}{dx}(μ(x)y)=μ(x)q(x). \label{Deq6} \]

Intégrez ensuite les deux côtés de l'équation \ ref {Deq6} par rapport à\(x\).

\[ \begin{align} ∫\dfrac{d}{dx}(μ(x)y)dx =∫μ(x)q(x)dx \\[4pt] μ(x)y =∫μ(x)q(x)dx \label{Deq7} \end{align} \]

Divisez les deux côtés de l'équation \ ref {Deq6} par\( μ(x)\) :

\[ y=\dfrac{1}{μ(x)}\left[∫μ(x)q(x)dx+C\right]. \nonumber \]

Comme\( μ(x)\) cela a été calculé précédemment, nous avons maintenant terminé. Remarque importante à propos de la constante d'intégration\( C\) : il peut sembler que nous ne sommes pas cohérents dans l'utilisation de la constante d'intégration. Cependant, l'intégrale impliquant\( p(x)\) est nécessaire afin de trouver un facteur d'intégration pour l'équation. Un seul facteur d'intégration est nécessaire pour résoudre l'équation ; il est donc prudent d'attribuer une valeur\(C\) pour cette intégrale. Nous avons choisi\(C=0\). Lors du calcul de l'intégrale entre crochets dans l'équation, il est nécessaire de garder ouvertes nos options pour la valeur de la constante d'intégration, car notre objectif est de trouver une famille générale de solutions à l'équation. C'est exactement ce que garantit ce facteur d'intégration.

Stratégie de résolution de problèmes : résolution d'une équation différentielle linéaire de premier ordre

1. Mettez l'équation sous forme standard et identifiez\( p(x)\) et\( q(x)\).
2. Calculer le facteur d'intégration\[ μ(x)=e^{∫p(x)dx}. \nonumber \]
3. Multipliez les deux côtés de l'équation différentielle par\( μ(x)\).
4. Intégrez les deux côtés de l'équation obtenue à l'étape\( 3\) et divisez les deux côtés par\( μ(x)\).
5. S'il existe une condition initiale, déterminez la valeur de\( C\).

Exemple\( \PageIndex{2}\): Solving a First-order Linear Equation

Trouvez une solution générale pour l'équation différentielle\( xy'+3y=4x^2−3x.\) Assume\( x>0.\)

Solution

1. Pour mettre cette équation différentielle sous forme standard, divisez les deux côtés par\( x\) :

\[ y'+\dfrac{3}{x}y=4x−3. \nonumber \]

Par conséquent\( p(x)=\dfrac{3}{x}\) et\( q(x)=4x−3.\)

2. Le facteur d'intégration est\( μ(x)=e^{∫(3/x)}dx=e^{3 \ln x}=x^3\).

3. La multiplication des deux côtés de l'équation différentielle par nous\( μ(x)\) donne

\[ \begin{align*} x^3y′+x^3(\dfrac{3}{x}) =x^3(4x−3) \\[4pt] x^3y′+3x^2y =4x^4−3x^3 \\[4pt] \dfrac{d}{dx}(x^3y) = 4x^4−3x^3. \end{align*}\]

4. Intégrez les deux côtés de l'équation.

\[ \begin{align*} ∫\dfrac{d}{dx}(x^3y)dx = ∫4x^4−3x^3dx \\[4pt] x^3y =\dfrac{4x^5}{5}−\dfrac{3x^4}{4}+C \\[4pt] y =\dfrac{4x^2}{5}−\dfrac{3x}{4}+Cx^{−3}. \end{align*}\]

5. Il n'y a pas de valeur initiale, donc le problème est résolu.

Analyse

Vous avez peut-être remarqué la condition qui a été imposée à l'équation différentielle ; à savoir,\( x>0\). Pour toute valeur non nulle de\( C\), la solution générale n'est pas définie à\( x=0\). De plus, quand\( x<0\), le facteur d'intégration change. Le facteur d'intégration est donné par l'équation as\( f(x)=e^{∫p(x)dx}\). Pour cela,\( p(x)\) nous obtenons

\[ \begin{align*} e^{∫p(x)dx} =e^{∫(3/x)dx} \\[4pt] =e^{3\ln|x|} \\[4pt] =|x|^3 \end{align*}\]

depuis\(x<0\). Le comportement de la solution générale change en\( x=0\) grande partie en raison du fait que cela n'y\( p(x)\) est pas défini.

Exercice\(\PageIndex{2}\)

Trouvez la solution générale à l'équation différentielle\( (x−2)y'+y=3x^2+2x.\) Assume\( x>2\).

Allusion

Utilisez la méthode décrite dans la stratégie de résolution de problèmes pour les équations différentielles linéaires de premier ordre.

Réponse

\( y=\dfrac{x^3+x^2+C}{x−2}\)

Nous utilisons maintenant la même stratégie pour trouver la solution à un problème de valeur initiale.

Exemple\( \PageIndex{3}\): A First-order Linear Initial-Value Problem

Résolvez le problème de la valeur initiale

\[ y′+3y=2x−1,y(0)=3. \nonumber \]

Solution

1. Cette équation différentielle est déjà sous forme standard avec\( p(x)=3\) et\( q(x)=2x−1\).

2. Le facteur d'intégration est\( μ(x)=e^{∫3dx}=e^{3x}\).

3. La multiplication des deux côtés de l'équation différentielle par\( μ(x)\) donne

\[ \begin{align*} e^{3x}y′+3e^{3x}y =(2x−1)e^{3x} \\[4pt] \dfrac{d}{dx}[ye^{3x}] =(2x−1)e^{3x}. \end{align*}\]

Intégrez les deux côtés de l'équation :

\( ∫\dfrac{d}{dx}[ye^{3x}]dx=∫(2x−1)e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}}{3}(2x−1)−∫\dfrac{2}{3}e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}(2x−1)}{3}−\dfrac{2e^{3x}}{9}+C\)

\( y=\dfrac{2x−1}{3}−\dfrac{2}{9}+Ce^{−3x}\)

\( y=\dfrac{2x}{3}−\dfrac{5}{9}+Ce^{−3x}\).

4. Maintenant, remplacez\( x=0\) et\( y=3\) insérez dans la solution générale et résolvez par\( C\) :

\[ \begin{align*} y =\dfrac{2}{3}x−\dfrac{5}{9}+Ce^{−3x} \\[4pt] 3 =\dfrac{2}{3}(0)−\dfrac{5}{9}+Ce^{−3(0)} \\[4pt] 3 =−\dfrac{5}{9}+C \\[4pt] C=\dfrac{32}{9}. \end{align*}\]

Par conséquent, la solution au problème de la valeur initiale est

\[ y=\dfrac{2}{3}x−\dfrac{5}{9}+\dfrac{32}{9}e^{−3x}. \nonumber \]

Exemple\(\PageIndex{4}\):

Résolvez le problème de la valeur initiale\[ y'−2y=4x+3y(0)=−2. \nonumber \]

Solution

\[ y=−2x−4+2e^{2x} \nonumber \]

Applications des équations différentielles linéaires du premier ordre

Nous examinons deux applications différentes des équations différentielles linéaires du premier ordre. Le premier concerne la résistance à l'air en ce qui concerne les objets qui montent ou descendent ; le second implique un circuit électrique. Les autres applications sont nombreuses, mais la plupart sont résolues de la même manière.

Chute libre avec résistance à l'air

Nous avons discuté de la résistance à l'air au début de cette section. L'exemple suivant montre comment appliquer ce concept à une balle en mouvement vertical. D'autres facteurs peuvent affecter la force de résistance de l'air, tels que la taille et la forme de l'objet, mais nous les ignorons ici.

Exemple\( \PageIndex{5}\): A Ball with Air Resistance

Une balle de racquetball est frappée directement vers le haut avec une vitesse initiale de\( 2\) m/s. La masse d'une balle de racquetball est d'environ\( 0.0427\) kg. La résistance de l'air agit sur la balle avec une force numériquement égale à\( 0.5v\), où\( v\) représente la vitesse de la balle à un moment donné\( t\).

1. Détermine la vitesse de la balle en fonction du temps.
2. Combien de temps faut-il pour que la balle atteigne sa hauteur maximale ?
3. Si la balle est frappée d'une hauteur initiale d'un\( 1\) mètre, quelle hauteur atteindra-t-elle ?

Solution

a. La masse\( m=0.0427kg,k=0.5,\) et\( g=9.8m/s^2\). La vitesse initiale est de\( v_0=2 m/s\). Par conséquent, le problème de la valeur initiale est

\( 0.0427\dfrac{dv}{dt}=−0.5v−0.0427(9.8),v_0=2.\)

Diviser l'équation différentielle par\( 0.0427\) donne

\( \dfrac{dv}{dt}=−11.7096v−9.8,v_0=2.\)

L'équation différentielle est linéaire. Utilisation de la stratégie de résolution de problèmes pour les équations aux dérivées linéaires :

Étape 1 Réécrivez l'équation différentielle comme suit\( \dfrac{dv}{dt}+11.7096v=−9.8\) : Cela donne\( p(t)=11.7096\) et\( q(t)=−9.8\)

Étape 2 Le facteur d'intégration est\( μ(t)=e^{∫11.7096dt}=e^{11.7096t}.\)

Étape 3. Multipliez l'équation différentielle par\( μ(t)\) :

\( e^{11.7096t\dfrac{dv}{dt}}+11.7096ve^{11.7096t}=−9.8e^{11.7096t}\)

\( \dfrac{d}{dt}[ve^{11.7096t}]=−9.8e^{11.7096t}.\)

Étape 4. Intégrez les deux côtés :

\( ∫\dfrac{d}{dt}[ve^{11.7096t}]dt=∫−9.8e^{11.7096t}dt\)

\( ve^{11.7096t}=\dfrac{−9.8}{11.7096}e^{11.7096t}+C\)

\( v(t)=−0.8369+Ce^{−11.7096t}.\)

Étape 5. Résolvez pour\( C\) utiliser la condition initiale\( v_0=v(0)=2\) :

\( v(t)=−0.8369+Ce^{−11.7096t}\)

\( v(0)=−0.8369+Ce^{−11.7096(0)}\)

\( 2=−0.8369+C\)

\( C=2.8369.\)

Par conséquent, la solution au problème de la valeur initiale est

\( v(t)=2.8369e^{−11.7096t}−0.8369.\)

b. La balle atteint sa hauteur maximale lorsque la vitesse est égale à zéro. La raison en est que lorsque la vitesse est positive, elle augmente, et lorsqu'elle est négative, elle diminue. Par conséquent, lorsqu'il est nul, il ne monte ni ne descend et se trouve à sa hauteur maximale :

\( 2.8369e^{−11.7096t}−0.8369=0\)

\( 2.8369e^{−11.7096t}=0.8369\)

\( e^{−11.7096t}=\dfrac{0.8369}{2.8369}≈0.295\)

\( lne^{−11.7096t}=ln0.295≈−1.221\)

\( −11.7096t=−1.221\)

\( t≈0.104.\)

Il faut donc environ une\( 0.104\) seconde pour atteindre la hauteur maximale.

c. Pour déterminer la hauteur de la balle en fonction du temps, utilisez le fait que la dérivée de la position est la vitesse, c'est-à-dire que si elle\( h(t)\) représente la hauteur dans le temps\( t\), alors\( h′(t)=v(t)\). Parce que nous connaissons\( v(t)\) et connaissons la hauteur initiale, nous pouvons créer un problème de valeur initiale :

\( h′(t)=2.8369e^{−11.7096t}−0.8369,h(0)=1.\)

Intégrer les deux côtés de l'équation différentielle par rapport à\( t\) donne

\( ∫h′(t)dt=∫2.8369e^{−11.7096t}−0.8369dt\)

\( h(t)=−\dfrac{2.8369}{11.7096}e^{−11.7096t}−0.8369t+C\)

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C.\)

Résolvez le problème\( C\) en utilisant la condition initiale :

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C\)

\( h(0)=−0.2423e^{−11.7096(0)}−0.8369(0)+C\)

\( 1=−0.2423+C\)

\( C=1.2423.\)

Par conséquent

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+1.2423.\)

Après\( 0.104\) une seconde, la hauteur est donnée par

\( h(0.2)=−0.2423e^{−11.7096t}−0.8369t+1.2423≈1.0836\)mètre.

Exercice\(\PageIndex{3}\)

Le poids d'un cent est de\(2.5\) grammes (United States Mint, « Coin Specifications », consulté le 9 avril 2015, http://www.usmint.gov/about_the_mint...specifications), et la terrasse d'observation supérieure de l'Empire State Building se trouve\( 369\) à quelques mètres au-dessus de la rue. Comme la pièce de monnaie est un objet petit et relativement lisse, la résistance à l'air agissant sur la pièce est en fait assez faible. Nous supposons que la résistance à l'air est numériquement égale à\( 0.0025v\). De plus, la pièce d'un cent est lâchée sans qu'aucune vitesse initiale ne lui soit communiquée.

1. Définissez un problème de valeur initiale qui représente la baisse d'un centime.
2. Résolvez le problème pour\( v(t)\).
3. Quelle est la vitesse terminale de la pièce d'un cent (c'est-à-dire, calculez la limite de la vitesse lorsque l'on\( t\) approche de l'infini) ?

Allusion

Configurez l'équation différentielle de la même manière que dans l'exemple. N'oubliez pas de convertir les grammes en kilogrammes.

Réponse

un.\( \dfrac{dv}{dt}=−v−9.8\)\( v(0)=0\)

b.\( v(t)=9.8(e^{−t}−1)\)

c.\( \lim_{t→∞}v(t)=\lim_{t→∞}(9.8(e^{−t}−1))=−9.8m/s≈−21.922mph\)

Circuits électriques

Une source de force électromotrice (par exemple, une batterie ou un générateur) produit un flux de courant dans un circuit fermé, et ce courant produit une chute de tension à travers chaque résistance, inductance et condensateur du circuit. La règle de boucle de Kirchhoff stipule que la somme des chutes de tension entre les résistances, les inducteurs et les condensateurs est égale à la force électromotrice totale dans un circuit fermé. Nous avons obtenu les trois résultats suivants :

1. La chute de tension aux bornes d'une résistance est donnée par

\( E_R=Ri,\)

où\( R\) se trouve une constante de proportionnalité appelée résistance, et\( i\) est le courant.

2. La chute de tension aux bornes d'une bobine d'induction est donnée par

\( EL=Li′\),

où\( L\) est une constante de proportionnalité appelée inductance, et désigne\( i\) à nouveau le courant.

3. La chute de tension aux bornes d'un condensateur est donnée par

\( E_C=\dfrac{1}{C}q\),

où\( C\) est une constante de proportionnalité appelée capacité, et\( q\) est la charge instantanée sur le condensateur. La relation entre\( i\) et\( q\) est\( i=q′\).

Nous utilisons des unités de volts\( (V)\) pour mesurer la tension\( E\), des ampères\( (A)\) pour mesurer le courant\( i\), des coulombs\( (C)\) pour mesurer la charge\( q\), des ohms\( (Ω)\) pour mesurer la résistance\( R\), des henrys\( (H)\) pour mesurer l'inductance\( L\) et des farads\( (F)\) pour mesurer capacité\( C\). Considérez le circuit de la figure\( \PageIndex{2}\).

Figure\( \PageIndex{2}\) : Un circuit électrique typique contenant un générateur de tension\( (V_S)\), un condensateur\( (C)\), un inducteur\( (L)\) et une résistance\( (R)\).

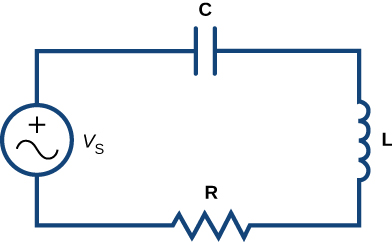
En appliquant la règle de boucle de Kirchhoff à ce circuit, nous\( E\) indiquons la force électromotrice fournie par le générateur de tension. Alors

\( E_L+E_R+E_C=E\).

En substituant les expressions pour\( E_L,E_R,\) et\( E_C\) dans cette équation, nous obtenons

\( Li′+Ri+\dfrac{1}{C}q=E.\)

S'il n'y a pas de condensateur dans le circuit, l'équation devient

\( Li′+R_i=E.\)

Il s'agit d'une équation différentielle du premier ordre dans\( i\). Le circuit est appelé\( LR\) circuit.

Ensuite, supposons qu'il n'y ait pas d'inductance dans le circuit, mais qu'il y ait un condensateur et une résistance, donc\( L=0,R≠0,\) et\( C≠0.\) puis l'équation peut être réécrite comme

\( Rq′+\dfrac{1}{C}q=E,\)

qui est une équation différentielle linéaire du premier ordre. C'est ce que l'on appelle un circuit RC. Dans les deux cas, nous pouvons configurer et résoudre un problème de valeur initiale.

Circuit électrique

Un circuit possède en série une force électromotrice fournie par\( E=50\sin 20tV,\) une résistance de\( 5Ω\), et un inducteur de\( 0.4H\). Si le courant initial est\( 0\), trouvez le courant à l'heure\( t>0\).

Solution

Nous avons une résistance et une inductance dans le circuit, nous utilisons donc l'équation. La chute de tension aux bornes de la résistance est donnée par\( E_R=R_i=5_i\). La chute de tension aux bornes de l'inducteur est donnée par\( E_L=Li′=0.4i′\). La force électromotrice devient le côté droit de l'équation. Donc, l'équation devient

\[ 0.4i′+5i=50\sin 20t. \nonumber \]

Diviser les deux côtés par\( 0.4\) donne l'équation

\[ i′+12.5i=125\sin 20t. \nonumber \]

Puisque le courant initial est 0, ce résultat donne une condition initiale de\( i(0)=0.\) Nous pouvons résoudre ce problème de valeur initiale en utilisant la stratégie en cinq étapes pour résoudre des équations différentielles du premier ordre.

Étape 1 Réécrivez l'équation différentielle comme suit\( i′+12.5i=125\sin 20t\) : Cela donne\( p(t)=12.5\) et\( q(t)=125\sin 20t\).

Étape 2 Le facteur d'intégration est\( μ(t)=e^{∫12.5dt}=e^{12.5t}\).

Étape 3. Multipliez l'équation différentielle par\( μ(t)\) :

\( e^{12.5t}i′+12.5e^{12.5t}i=125e^{12.5t}\sin 20t\)

\( \dfrac{d}{dt}[ie^{12.5}t]=125e^{12.5t}\sin 20t\).

Étape 4. Intégrez les deux côtés :

\( ∫\dfrac{d}{dt}[ie^{12.5t}]dt=∫125e^{12.5t}\sin 20tdt\)

\( ie^{12.5t}=(\dfrac{250\sin 20t−400\cos 20t}{89})e^{12.5t}+C\)

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\).

Étape 5. Résolvez pour\( C\) utiliser la condition initiale\( v(0)=2\) :

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\)

\( i(0)=\dfrac{250sin20(0)−400cos20(0)}{89}+Ce^{−12.5(0)}\)

\( 0=−\dfrac{400}{89}+C\)

\( C=\dfrac{400}{89}\).

Par conséquent, la solution au problème de la valeur initiale est

\[ i(t)=\dfrac{250\sin 20t−400\cos 20t+400e^{−12.5t}}{89}=\dfrac{250\sin 20t−400\cos 20t}{89}+\dfrac{400e^{−12.5t}}{89}. \nonumber \]

Le premier terme peut être réécrit sous la forme d'une fonction cosinusoïdale unique. Tout d'abord, multipliez et divisez par\( \sqrt{250^2+400^2}=50\sqrt{89}\) :

\( \dfrac{250\sin 20t−400\cos 20t}{89}=\dfrac{50\sqrt{89}}{89}(\dfrac{250\sin 20t−400\cos 20t}{50\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})\).

Ensuite,\( φ\) définissez-le comme étant un angle aigu tel que\( \cos φ=\dfrac{8}{\sqrt{89}}\). Puis\( \sin φ=\dfrac{5}{\sqrt{89}}\) et

\( −\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\cos φ\cos 20t−\sin φ\sin 20t)=−\dfrac{50\sqrt{89}}{89}\cos(20t+φ).\)

Par conséquent, la solution peut être écrite sous la forme

\( i(t)=−\dfrac{50\sqrt{89}}{89}cos(20t+φ)+\dfrac{400e^{−12.5t}}{89}\).

Le second terme est appelé terme d'atténuation, car il disparaît rapidement à\( t\) mesure qu'il grandit. Le décalage de phase est donné par\( φ\), et l'amplitude du courant en régime permanent est donnée par\( \dfrac{50\sqrt{89}}{89}\). Le graphique de cette solution apparaît dans la figure\( \PageIndex{3}\) :

Chiffre\( \PageIndex{3}\).

Exercice\(\PageIndex{4}\)

Un circuit possède en série une force électromotrice donnée par\( E=20sin5t\) V, un condensateur\( 0.02F\) ayant une capacité et une résistance de\( 8Ω\). Si la charge initiale est\( 4C\), trouvez la charge à un moment donné\( t>0\).

Allusion

Utilisez l'équation pour un\( RC\) circuit afin de configurer un problème de valeur initiale.

Réponse

Problème de valeur initiale :

\( 8q′+\dfrac{1}{0.02}q=20sin5t,q(0)=4\)

\( q(t)=\dfrac{10sin5t−8cos5t+172e^{−6.25t}}{41}\)

Concepts clés

• Toute équation différentielle linéaire du premier ordre peut être écrite sous la forme\( y'+p(x)y=q(x)\).
• Nous pouvons utiliser une stratégie de résolution de problèmes en cinq étapes pour résoudre une équation différentielle linéaire de premier ordre qui peut inclure ou non une valeur initiale.
• Les applications des équations différentielles linéaires du premier ordre incluent la détermination du mouvement d'un objet ascendant ou descendant avec une résistance à l'air et la recherche du courant dans un circuit électrique.

Équations clés

• formulaire standard

\( y'+p(x)y=q(x)\)

• facteur d'intégration

\( μ(x)=e^{∫p(x)dx}\)

Lexique

facteur d'intégration

toute fonction\(f(x)\) qui est multipliée des deux côtés d'une équation différentielle pour que le côté impliquant la fonction inconnue soit égal à la dérivée du produit de deux fonctions

linéaire

description d'une équation différentielle du premier ordre qui peut être écrite sous la forme\( a(x)y′+b(x)y=c(x)\)

formulaire standard

la forme d'une équation différentielle linéaire du premier ordre obtenue en écrivant l'équation différentielle dans la forme\( y'+p(x)y=q(x)\)