8.3 : Équations séparables
- Page ID
- 197445
- Utilisez la séparation des variables pour résoudre une équation différentielle.
- Résolvez des applications en séparant les variables.
Nous examinons maintenant une technique de solution permettant de trouver des solutions exactes à une classe d'équations différentielles appelées équations différentielles séparables. Ces équations sont communes à une grande variété de disciplines, notamment la physique, la chimie et l'ingénierie. Nous illustrons quelques applications à la fin de la section.
Séparation des variables
Nous commençons par une définition et quelques exemples.
Une équation différentielle séparable est toute équation qui peut être écrite sous la forme
\[y'=f(x)g(y). \label{sep} \]
Le terme « séparable » fait référence au fait que le côté droit de l'équation \ ref {sep} peut être séparé en une fonction de\(x\) fois une fonction de\(y\). Voici des exemples d'équations différentielles séparables
\[ \begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align} \]
L'équation \ ref {eq2} est séparable avec\(f(x)=6x^2+4x\) et\(g(y)=1\), l'équation \ ref {eq3} est séparable avec\(f(x)=1\)\(g(y)=\sec y+\tan y,\) et et le côté droit de l'équation \ ref {eq4} peut être factorisé comme\((x+3)(y−2)\), donc elle est également séparable. L'équation \ ref {eq3} est également appelée équation différentielle autonome parce que le côté droit de l'équation est fonction de la\(y\) seule. Si une équation différentielle est séparable, il est alors possible de la résoudre en utilisant la méthode de séparation des variables.
- Vérifiez toutes les valeurs\(y\) qui font que\(g(y)=0.\) celles-ci correspondent à des solutions constantes.
- Réécrivez l'équation différentielle dans le formulaire\[ \dfrac{dy}{g(y)}=f(x)dx. \nonumber \]
- Intégrez les deux côtés de l'équation.
- Résolvez l'équation résultante\(y\) si possible.
- Si une condition initiale existe, remplacez les valeurs appropriées par\(x\) et\(y\) dans l'équation et résolvez pour la constante.
Notez que l'étape 4 indique « Résolvez l'équation résultante\(y\) si possible ». Il n'est pas toujours possible d'obtenir\(y\) en fonction explicite de\(x\). Très souvent, nous devons nous contenter de trouver y en tant que fonction implicite de\(x\).
Trouvez une solution générale à l'équation différentielle à\(y'=(x^2−4)(3y+2)\) l'aide de la méthode de séparation des variables.
Solution
Suivez la méthode en cinq étapes pour séparer les variables.
1. Dans cet exemple,\(f(x)=x^2−4\) et\(g(y)=3y+2\). \(g(y)=0\)Le réglage donne\(y=−\dfrac{2}{3}\) comme solution constante.
2. Réécrivez l'équation différentielle dans le formulaire
\[ \dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber \]
3. Intégrez les deux côtés de l'équation :
\[ ∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber \]
Laissez\(u=3y+2\). Alors\(du=3\dfrac{dy}{dx}\,dx\), l'équation devient
\[ \dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber \]
\[ \dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber \]
\[ \dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber \]
4. Pour résoudre cette équation\(y\), multipliez d'abord les deux côtés de l'équation par\(3\).
\[ \ln|3y+2|=x^3−12x+3C\nonumber \]
Nous utilisons maintenant une certaine logique pour gérer la constante\(C\). Puisque\(C\) représente une constante arbitraire, représente\(3C\) également une constante arbitraire. Si nous appelons la deuxième constante arbitraire\(C_1,\) où\(C_1 = 3C,\) l'équation devient
\[ \ln|3y+2|=x^3−12x+C_1.\nonumber \]
Maintenant, exponentiez les deux côtés de l'équation (c'est-à-dire, faites de chaque côté de l'équation l'exposant de la base\(e\)).
\[ \begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}\]
Définissez à nouveau une nouvelle constante\(C_2= e^{C_1}\) (notez que\(C_2 > 0\)) :
\[ |3y+2|=C_2e^{x^3−12x}.\nonumber \]
En raison de la valeur absolue sur le côté gauche de l'équation, cela correspond à deux équations distinctes :
\[3y+2=C_2e^{x^3−12x}\nonumber \]
et
\[3y+2=−C_2e^{x^3−12x}.\nonumber \]
La solution de l'une ou l'autre équation peut être écrite sous la forme
\[y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber \]
Puisque\(C_2>0\), peu importe que nous utilisions plus ou moins, la constante peut en fait avoir l'un ou l'autre signe. De plus, l'indice de la constante\(C\) est totalement arbitraire et peut être supprimé. Par conséquent, la solution peut être écrite sous la forme
\[ y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber \]
Notez qu'en écrivant une solution générale unique de cette manière, nous permettons également\(C\) d'égaliser\(0\). Cela nous donne la solution singulière\(y = -\dfrac{2}{3}\), pour l'équation différentielle donnée. Vérifiez qu'il s'agit bien d'une solution de cette équation différentielle !
5. Aucune condition initiale n'est imposée, nous avons donc terminé.
Utilisez la méthode de séparation des variables pour trouver une solution générale à l'équation différentielle
\[ y'=2xy+3y−4x−6. \nonumber \]
- Allusion
-
Facturez d'abord le côté droit de l'équation en regroupant, puis utilisez la stratégie en cinq étapes de séparation des variables.
- Réponse
-
\[ y=2+Ce^{x^2+3x} \nonumber \]
En utilisant la méthode de séparation des variables, résolvez le problème de la valeur initiale
\[ y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber \]
Solution
Suivez la méthode en cinq étapes pour séparer les variables.
1. Dans cet exemple,\(f(x)=2x+3\) et\(g(y)=y^2−4\). \(g(y)=0\)Le réglage donne\(y=±2\) comme solutions constantes.
2. Divisez les deux côtés de l'équation par\(y^2−4\) et multipliez par\(dx\). Cela donne l'équation
\[\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber \]
3. Intégrez ensuite les deux côtés :
\[∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2} \]
Pour évaluer le côté gauche, utilisez la méthode de décomposition par fraction partielle. Cela conduit à l'identité
\[\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber \]
Ensuite, l'équation \ ref {Ex2.2} devient
\[\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber \]
\[\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber \]
En multipliant les deux côtés de cette équation par\(4\) et en\(4C\) remplaçant\(C_1\) par
\[\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber \]
\[\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber \]
4. Il est possible de résoudre cette équation pour d'\(y.\)abord exponentier les deux côtés de l'équation et définir\(C_2=e^{C_1}\) :
\[\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber \]
Ensuite, nous pouvons supprimer la valeur absolue et laisser une nouvelle constante\(C_3\) être positive, négative ou nulle,\(C_3 =\pm C_2\) c'est-à-dire\(C_3 = 0.\)
Multipliez ensuite les deux côtés par\(y+2\).
\[y−2=C_3(y+2)e^{4x^2+12x}\nonumber \]
\[y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber \]
Maintenant, collectez tous les termes impliquant d'un\(y\) côté de l'équation et résolvez pour\(y\) :
\[y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber \]
\[y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber \]
\[y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber \]
5. Pour déterminer la valeur de la solution générale\(C_3\), la remplacer\(x=0\) et l'\(y=−1\)intégrer. Sinon, nous pouvons placer les mêmes valeurs dans une équation précédente, à savoir l'équation\(\dfrac{y−2}{y+2}=C_3e^{4x^2+12}\). C'est beaucoup plus facile à résoudre pour\(C_3\) :
\[\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber \]
\[\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber \]
\[C_3=−3.\nonumber \]
Par conséquent, la solution au problème de la valeur initiale est
\[y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber \]
Un graphique de cette solution apparaît dans la figure\(\PageIndex{1}\).
![Un graphique de la solution sur [-5, 3] pour x et [-3, 2] pour y. Il commence par une ligne horizontale à y = -2 de x = -5 à juste avant -3, remonte presque immédiatement jusqu'à y = 2 de juste après x = -3 à juste avant x = 0, et redescend presque immédiatement jusqu'à y = -2 juste après x = 0 à x = 3.](https://math.libretexts.org/@api/deki/files/7854/imageedit_2_3087334010.png)
Trouvez la solution au problème de la valeur initiale
\[ 6y'=(2x+1)(y^2−2y−8) \nonumber \]
en\(y(0)=−3\) utilisant la méthode de séparation des variables.
- Allusion
-
Suivez les étapes de séparation des variables afin de résoudre le problème de la valeur initiale.
- Réponse
-
\[ y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber \]
Applications de la séparation des variables
De nombreux problèmes intéressants peuvent être décrits par des équations séparables. Nous illustrons deux types de problèmes : les concentrations des solutions et la loi de Newton sur le refroidissement.
Concentrations de
Imaginons qu'un réservoir soit rempli d'une solution saline. Nous aimerions déterminer la quantité de sel présente dans le réservoir en fonction du temps. Nous pouvons appliquer le processus de séparation des variables pour résoudre ce problème et des problèmes similaires impliquant des concentrations de solution.
Un réservoir contenant 1\(100\) L d'une solution de saumure contient initialement\(4\) 1 kg de sel dissous dans la solution. À un moment\(t=0\) donné, une autre solution de saumure s'écoule dans le réservoir à un débit de\(2\) L/min. Cette solution de saumure contient une concentration de\(0.5\) kg/L de sel. Dans le même temps, un robinet est ouvert au bas du réservoir, permettant à la solution combinée de s'écouler à un débit de\(2\) L/min, de sorte que le niveau de liquide dans le réservoir reste constant (Figure\(\PageIndex{2}\)). Déterminez la quantité de sel dans le réservoir en fonction du temps (mesurée en minutes) et déterminez la quantité limite de sel dans le réservoir, en supposant que la solution dans le réservoir soit bien mélangée à tout moment.
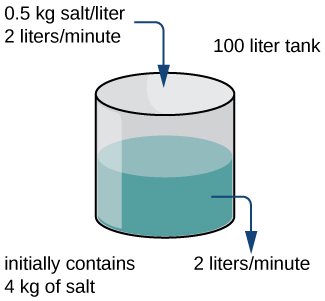
Solution
Nous définissons d'abord une fonction\(u(t)\) qui représente la quantité de sel en kilogrammes dans le réservoir en fonction du temps. \(\dfrac{du}{dt}\)Représente ensuite la vitesse à laquelle la quantité de sel dans le réservoir change en fonction du temps. \(u(0)\)Représente également la quantité de sel dans le réservoir à la fois\(t=0\), qui est en\(4\) kilogrammes.
La configuration générale de l'équation différentielle que nous allons résoudre est de la forme
\[\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber \]
Le TAUX D'ENTRÉE représente la vitesse à laquelle le sel entre dans le réservoir et le DÉBIT DE SORTIE représente le débit auquel le sel quitte le réservoir. Comme la solution entre dans le réservoir à un débit de\(2\) L/min et que chaque litre de solution contient un\(0.5\) kilogramme de sel, chaque\(2(0.5)=1\) kilogramme de sel entre dans le réservoir chaque minute. Par conséquent, TAUX D'ENTRÉE =\(1\).
Pour calculer la vitesse à laquelle le sel quitte le réservoir, nous avons besoin de la concentration de sel dans le réservoir à tout moment. Comme la quantité réelle de sel varie au fil du temps, la concentration de sel varie également. Cependant, le volume de la solution reste fixé à 100 litres. Le nombre de kilogrammes de sel dans le réservoir à la fois\(t\) est égal à\(u(t)\). Ainsi, la concentration en sel est de\(\dfrac{u(t)}{100}\) kg/L et la solution quitte le réservoir à un débit de\(2\) L/min. Par conséquent, le sel quitte le réservoir à un débit de\(\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}\) kg/min, et le débit sortant est égal à\(\dfrac{u(t)}{50}\). Par conséquent, l'équation différentielle devient\(\dfrac{du}{dt}=1−\dfrac{u}{50}\), et la condition initiale est\(u(0)=4.\) Le problème de la valeur initiale à résoudre est
\[\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber \]
L'équation différentielle est une équation séparable, nous pouvons donc appliquer la stratégie en cinq étapes pour trouver une solution.
Étape 1. \(1−\dfrac{u}{50}=0\)Le réglage donne\(u=50\) comme solution constante. Comme la quantité initiale de sel dans le réservoir est de\(4\) kilogrammes, cette solution ne s'applique pas.
Étape 2. Réécrivez l'équation comme
\[\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber \]
Multipliez ensuite les deux côtés par\(dt\) et divisez les deux côtés par\(50−u:\)
\[\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber \]
Étape 3. Intégrez les deux côtés :
\[\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}\]
Étape 4. Résolvez pour\(u(t)\) :
\[\ln|50−u|=−\dfrac{t}{50}−C\nonumber \]
\[e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber \]
\[|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber \]
Éliminez la valeur absolue en laissant la constante être positive, négative ou nulle, c'est-à-dire\(C_1 = \pm e^{-C}\) ou\(C_1 = 0\) :
\[50−u=C_1e^{−t/50}.\nonumber \]
Enfin, résolvez les problèmes\(u(t)\) suivants :
\[u(t)=50−C_1e^{−t/50}.\nonumber \]
Étape 5. Résolvez pour\(C_1\) :
\[\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}\]
La solution au problème de la valeur initiale est :\(u(t)=50−46e^{−t/50}.\) Pour déterminer la quantité limite de sel dans le réservoir, prenez la limite à mesure que l'infini se\(t\) rapproche de l'infini :
\[\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}\]
Notez que c'était la solution constante de l'équation différentielle. Si la quantité initiale de sel dans le réservoir est de\(50\) kilogrammes, elle reste constante. S'il commence à moins de\(50\) kilogrammes, il approche les\(50\) kilogrammes au fil du temps.
Un réservoir contient des\(3\) kilogrammes de sel dissous dans des\(75\) litres d'eau. Une solution saline de\(0.4\) kg de sel/L est pompée dans le réservoir à un débit de\(6\) L/min et est drainée au même débit. Résolvez la concentration de sel à un moment donné\(t\). Supposons que le réservoir soit bien mélangé à tout moment.
- Allusion
-
Suivez les étapes de l'exemple\(\PageIndex{3}\) et déterminez une expression pour les flux entrants et sortants. Formulez un problème de valeur initiale, puis résolvez-le.
Problème de valeur initiale :
\[ \dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber \]
- Réponse
-
\[u(t)=30−27e^{−t/50} \nonumber \]
Loi du refroidissement de Newton
La loi de Newton sur le refroidissement indique que le taux de variation de la température d'un objet est proportionnel à la différence entre sa propre température et la température ambiante (c'est-à-dire la température de son environnement). Si nous laissons\(T(t)\) représenter la température d'un objet en fonction du temps, cela\(\dfrac{dT}{dt}\) représente la vitesse à laquelle cette température change. La température de l'environnement de l'objet peut être représentée par\(T_s\). Ensuite, la loi de refroidissement de Newton peut être écrite sous la forme
\[ \dfrac{dT}{dt}=k(T(t)−T_s) \nonumber \]
ou tout simplement
\[ \dfrac{dT}{dt}=k(T−T_s). \nonumber \]
La température de l'objet au début de toute expérience est la valeur initiale du problème de valeur initiale. C'est ce que nous appelons température\(T_0\). Par conséquent, le problème de valeur initiale qui doit être résolu prend la forme
\[ \dfrac{dT}{dt}=k(T−T_s) \label{newton} \]
avec\(T(0)=T_0\), où\(k\) se trouve une constante qui doit être donnée ou déterminée dans le contexte du problème. Nous utilisons ces équations dans l'exemple\(\PageIndex{4}\).
Une pizza est retirée du four après une cuisson complète, et la température du four est\(350°F.\) La température de la cuisine est\(75°F\), et après\(5\) quelques minutes, la température de la pizza est\(340°F\). Nous aimerions attendre que la température de la pizza atteigne\(300°F\) avant de la couper et de la servir (Figure\(\PageIndex{3}\)). Combien de temps devrons-nous encore attendre ?

Solution
La température ambiante (température ambiante) est\(75°F\) donc\(T_s=75\). La température de la pizza à la sortie du four est de\(350°F\), qui est la température initiale (c'est-à-dire la valeur initiale), donc\(T_0=350\). Par conséquent, l'équation \ ref {newton} devient
\[\dfrac{dT}{dt}=k(T−75) \nonumber \]
avec\(T(0)=350.\)
Pour résoudre l'équation différentielle, nous utilisons la technique en cinq étapes pour résoudre des équations séparables.
1. Mettre le côté droit à zéro donne\(T=75\) une solution constante. Puisque la pizza commence à partir de là,\(350°F,\) ce n'est pas la solution que nous cherchons.
2. Réécrivez l'équation différentielle en multipliant les deux côtés par\(dt\) et en divisant les deux côtés par\(T−75\) :
\[\dfrac{dT}{T−75}=k\,dt. \nonumber \]
3. Intégrez les deux côtés :
\[\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber \]
4. Résolvez le problème en commençant\(T\) par exponentier les deux côtés :
\[\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber \]
5. Résolvez le problème\(C\) en utilisant la condition initiale\(T(0)=350:\)
\[\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber \]
Par conséquent, la solution au problème de la valeur initiale est
\[T(t)=75+275e^{kt}.\nonumber \]
Pour déterminer la valeur de\(k\), nous devons utiliser le fait qu'au bout de\(5\) quelques minutes, la température de la pizza est\(340°F\). Par conséquent, en\(T(5)=340.\) substituant ces informations dans la solution au problème de la valeur initiale, nous avons
\[T(t)=75+275e^{kt}\nonumber \]
\[T(5)=340=75+275e^{5k}\nonumber \]
\[265=275e^{5k}\nonumber \]
\[e^{5k}=\dfrac{53}{55}\nonumber \]
\[\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber \]
\[5k=\ln(\dfrac{53}{55})\nonumber \]
\[k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber \]
Alors maintenant, nous avons\(T(t)=75+275e^{−0.007048t}.\) Quelle est la température\(300°F\) ? Résoudre car\(t,\) nous trouvons
\[T(t)=75+275e^{−0.007048t}\nonumber \]
\[300=75+275e^{−0.007048t}\nonumber \]
\[225=275e^{−0.007048t}\nonumber \]
\[e^{−0.007048t}=\dfrac{9}{11}\nonumber \]
\[\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber \]
\[−0.007048t=\ln\dfrac{9}{11}\nonumber \]
\[t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber \]
Par conséquent, nous devons attendre\(23.5\) quelques minutes supplémentaires (après que la température de la pizza ait atteint\(340°F\)). Cela devrait être juste assez de temps pour terminer ce calcul.
Un gâteau est retiré du four après une cuisson complète et la température du four est de\(450°F\). La température de la cuisine est\(70°F\), et après\(10\) quelques minutes, la température du gâteau est\(430°F\).
- Écrivez le problème de valeur initiale approprié pour décrire cette situation.
- Résolvez le problème de la valeur initiale pour\(T(t)\).
- Combien de temps faudra-t-il pour que la température du gâteau soit inférieure à\(5°F\) la température ambiante ?
- Allusion
-
Déterminez les valeurs de\(T_s\)\(T_0\) puis utilisez l'équation \ ref {newton}.
- Répondez à une
-
Problème de valeur initiale\[\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber \]
- Réponse b
-
\[T(t)=70+380e^{kt}\nonumber \]
- Réponse c
-
Quelques\(114\) minutes environ.
Concepts clés
- Une équation différentielle séparable est toute équation qui peut être écrite sous la forme\(y'=f(x)g(y).\)
- La méthode de séparation des variables est utilisée pour trouver la solution générale à une équation différentielle séparable.
Équations clés
- Équation différentielle séparable
\(y′=f(x)g(y)\)
- concentration de la solution
\(\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}\)
- La loi de Newton sur le refroidissement
\(\dfrac{dT}{dt}=k(T−T_s)\)
Lexique
- équation différentielle autonome
- une équation dans laquelle le côté droit est fonction de\(y\) seul
- équation différentielle séparable
- toute équation pouvant être écrite dans le formulaire\(y'=f(x)g(y)\)
- séparation des variables
- une méthode utilisée pour résoudre une équation différentielle séparable


