8.2E : Exercices pour la section 8.2

Last updated
Save as PDF

Page ID: 197473

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices 1 à 3, utilisez le champ de direction ci-dessous à partir de l'équation différentielle$ y'=−2y.$ Esquissez le graphique de la solution pour les conditions initiales données.

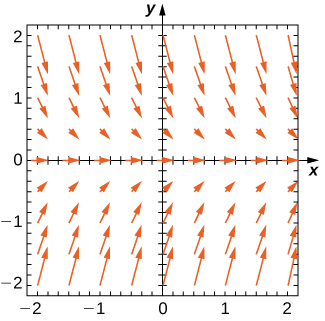
$Un champ de direction avec des flèches horizontales pointant vers la droite à 0. Les flèches au-dessus de l'axe x pointent vers le bas et vers la droite. Plus on s'éloigne de l'axe X, plus les flèches sont raides et plus elles sont proches de l'axe X, plus les flèches sont plates. De même, les flèches situées sous l'axe x pointent vers le haut et vers la droite. Plus on s'éloigne de l'axe X, plus les flèches sont raides et plus elles sont proches de l'axe X, plus les flèches sont plates.$

1)$ y(0)=1$

2)$ y(0)=0$

Réponse: 0. Plus elles sont proches de l'axe x, plus les flèches sont horizontales et plus elles sont éloignées, plus elles deviennent verticales." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_203.jpeg">

3)$ y(0)=−1$

4) Y a-t-il des équilibres entre les solutions de l'équation différentielle des exercices 1 à 3 ? Énumérez tous les équilibres ainsi que leur stabilité.

Réponse: $ y=0$est un équilibre stable

Pour les exercices 5 à 7, utilisez le champ de direction ci-dessous à partir de l'équation différentielle$ y'=y^2−2y$. Esquissez le graphique de la solution pour les conditions initiales données.

Un champ de direction avec des flèches horizontales à y = 0 et y = 2. Les flèches pointent vers le haut pour y 2 et pour y < 0. Les flèches pointent vers le bas pour 0 < y < 2. Plus les flèches sont proches de ces lignes, plus elles sont horizontales et plus elles sont éloignées, plus les flèches sont verticales." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_205.jpeg">

5)$ y(0)=3$

6)$ y(0)=1$

Réponse: 2 et pour y < 0. Les flèches pointent vers le bas pour 0 < y < 2. Plus les flèches sont proches de ces lignes, plus elles sont horizontales et plus elles sont éloignées, plus les flèches sont verticales. Une solution est esquissée qui suit y = 2 dans le quadrant deux, traverse (0, 1), puis suit l'axe des x." style="width: 319px; height: 320px;" width="319px" height="320px" src="https://math.libretexts.org/@api/dek...08_02_207.jpeg">

7)$ y(0)=−1$

8) Y a-t-il des équilibres entre les solutions de l'équation différentielle des exercices 5 à 7 ? Énumérez tous les équilibres ainsi que leur stabilité.

Réponse: $ y=0$est un équilibre stable et$ y=2$ est instable

Dans les exercices 9 à 13, dessinez le champ de direction pour les équations différentielles suivantes, puis résolvez l'équation différentielle. Dessinez votre solution au-dessus du champ de direction. Est-ce que votre solution suit les flèches de votre champ de direction ?

9)$ y'=t^3$

10)$ y'=e^t$

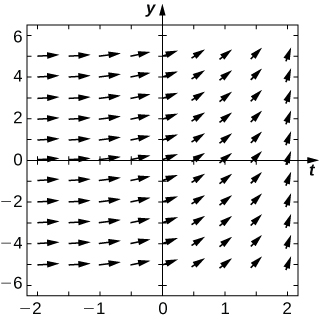
Réponse: $Un champ de direction couvrant les quatre quadrants. Au fur et à mesure que t passe de 0 à l'infini, les flèches deviennent de plus en plus verticales après avoir été horizontales plus proches de x = 0.$

11)$ \dfrac{dy}{dx}=x^2\cos x$

(12)$ \dfrac{dy}{dt}=te^t$

Réponse: $Un champ de direction au-dessus de [-2, 2] sur les axes x et y. Les flèches pointent légèrement vers le bas et vers la droite au-dessus de [-2, 0] et deviennent progressivement verticales au-dessus de [0, 2].$

13)$ \dfrac{dx}{dt}=\cosh(t)$

Dans les exercices 14 à 18, dessinez le champ directionnel pour les équations différentielles suivantes. Que pouvez-vous dire à propos du comportement de la solution ? Y a-t-il des équilibres ? Quelle est la stabilité de ces équilibres ?

(14)$ y'=y^2−1$

Réponse: Il semble y avoir un équilibre entre$y = -1$ (stable) et$y = 1$ (instable).
1. Les flèches pointent vers le bas pour -1 < y < 1. Plus les flèches sont proches de ces lignes, plus elles sont horizontales et plus elles sont éloignées, plus elles sont verticales." style="width: 342px; height: 344px;" width="342px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_214.jpeg">

15)$ y'=y−x$

16)$ y'=1−y^2−x^2$

Réponse: Il ne semble pas y avoir d'équilibre.
$Champ de direction avec des flèches pointant vers le bas et vers la droite pour presque tous les points situés dans [-2, 2] sur les axes x et y. Près de l'origine, les flèches deviennent plus horizontales, pointent vers le coin supérieur droit, deviennent plus horizontales, puis pointent de nouveau vers la droite vers le bas.$

17)$ y'=t^2\sin y$

18)$ y'=3y+xy$

Réponse: Il semble y avoir un équilibre instable à$y=0.$
-3, les flèches pointent vers le haut. En dessous de l'axe x et pour x < -3, les flèches pointent vers le haut. Pour x > -3, les flèches pointent vers le bas. Plus on s'éloigne de l'axe x et que x = -3, plus les flèches deviennent verticales, et plus elles se rapprochent, plus elles deviennent horizontales." style="width: 405px; height: 344px;" width="405px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_218.jpeg">

Faites correspondre le champ de direction aux équations différentielles données. Expliquez vos choix.

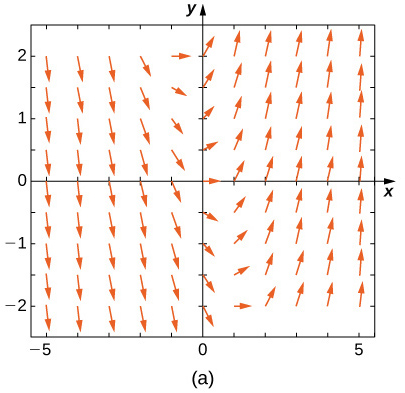
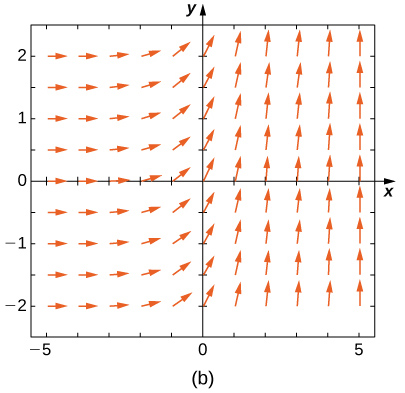
$Champ de direction avec des flèches pointant vers le bas et vers la droite dans les quadrants deux et trois. Après avoir traversé l'axe y, les flèches changent de direction et pointent vers la droite.$ $Champ de direction avec des flèches horizontales pointant vers la gauche dans les quadrants deux et trois. 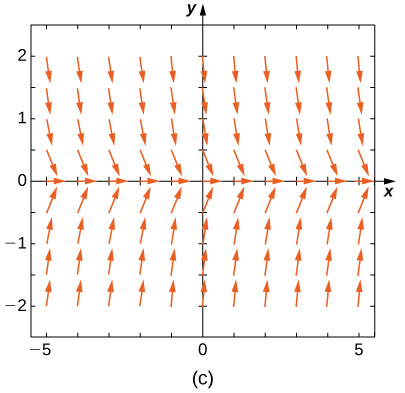En croisant l'axe y, les flèches changent et pointent vers le haut, dans les quadrants 1 et 4.$ $Champ de direction avec des flèches horizontales pointant vers la droite sur l'axe x. Au-dessus, les flèches pointent vers le bas et vers la droite, et en dessous, les flèches pointent vers le haut et vers la droite. 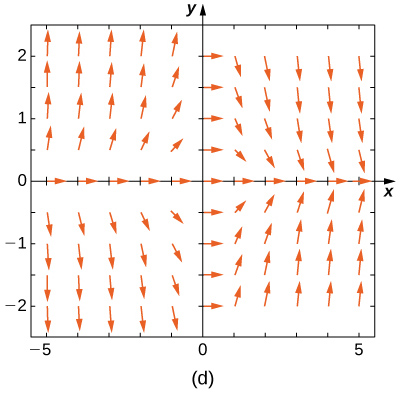Plus on s'éloigne de l'axe X, plus les flèches deviennent verticales.$ $Un champ de direction avec des flèches horizontales sur les axes x et y. Les flèches pointent vers le bas et vers la droite dans les quadrants 1 et 3. 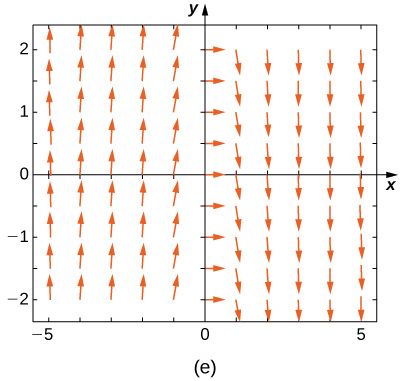Ils pointent vers le haut et vers la droite dans les quadrants deux et quatre.$ $Champ de direction avec des flèches pointant vers le haut dans les quadrants deux et trois, vers la droite sur l'axe y et vers le bas dans les quadrants un et quatre.$

19)$ y'=−3y$

(20)$ y'=−3t$

Réponse: $ E$

(21)$ y'=e^t$

(22)$ y'=\frac{1}{2}y+t$

Réponse: $ A$

23)$ y'=−ty$

Faites correspondre le champ de direction aux équations différentielles données. Expliquez vos choix.

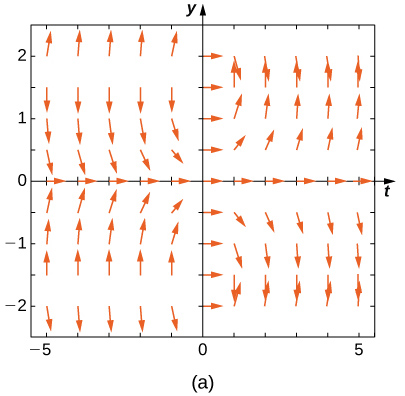
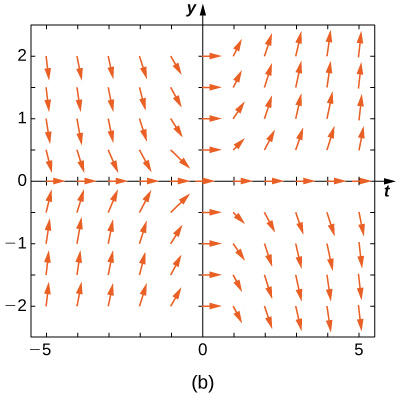
$Champ de direction avec des flèches horizontales pointant vers la droite sur les axes x et y. Dans les quadrants un et trois, les flèches pointent vers le haut, et dans les quadrants deux et quatre, elles pointent vers le bas.$ $Champ de direction avec des flèches horizontales pointant vers la droite sur les axes x et y. 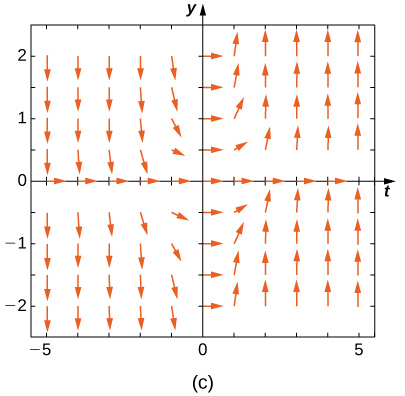Dans les quadrants un et trois, les flèches pointent vers le haut et vers la droite, et dans les quadrants deux et quatre, les flèches pointent vers le bas et vers la droite.$ $Champ de direction avec des flèches horizontales pointant vers la droite sur les axes x et y. 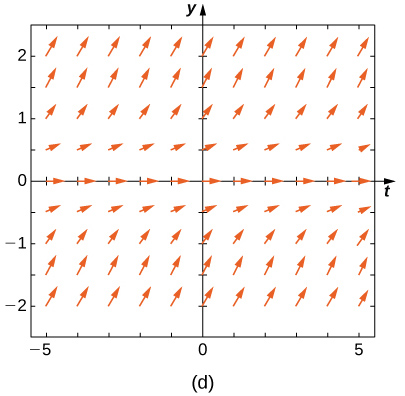Dans les quadrants deux et trois, les flèches pointent vers le bas, et dans les quadrants un et quatre, les flèches pointent vers le haut.$ $Champ de direction avec des flèches horizontales pointant vers la droite sur l'axe x. Les flèches pointent vers le haut et vers la droite dans tous les quadrants. Plus les flèches sont proches de l'axe x, plus elles sont horizontales et plus elles sont éloignées, plus elles sont verticales.$ 1,5 et x < 0, pour y < -1,5 et x < 0, et pour -1,5 < y < 1.5 and x > 0-, les flèches pointent vers le bas. Pour y> 1,5 et x > 0, pour y < -1,5, pour y < -1.5 and x > 0, et pour -1,5 < y < 1,5 et x < 0, les flèches pointent vers le haut." style="width: 405px; height: 380px;" width="405px" height="380px" src="https://math.libretexts.org/@api/dek...8_02_220e.jpeg">

(24)$ y'=t\sin y$

Réponse: $ B$

25)$ y'=−t\cos y$

(26)$ y'=t\tan y$

Réponse: $ A$

(27)$ y'=\sin^2y$

(28)$ y'=y^2t^3$

Réponse: $ C$

Estimez les solutions suivantes à l'aide de la méthode d'Euler avec des$ n=5$ étapes sur l'intervalle$ t=[0,1].$ Si vous êtes en mesure de résoudre exactement le problème de la valeur initiale, comparez votre solution à la solution exacte. Si vous ne parvenez pas à résoudre le problème de la valeur initiale, la solution exacte vous sera fournie pour que vous puissiez la comparer avec la méthode d'Euler. Quelle est la précision de la méthode d'Euler ?

(29)$ y'=−3y,\quad y(0)=1$

(30)$ y'=t^2,\quad y(0)=1$

Réponse: $ 2.24,$exact :$ 3$

Solution :

31) La solution$ y′=3t−y,\quad y(0)=1.$ exacte est$ y=3t+4e^{−t}−3$

32) La solution$ y′=y+t^2,\quad y(0)=3.$ exacte est$ y=5e^t−2−t^2−2t$

Réponse: $ 7.739364,$exact :$ 5(e−1)$

33)$ y′=2t,\quad y(0)=0$

34) [T] La solution$ y'=e^{x+y},y(0)=−1.$ exacte est$ y=−\ln(e+1−e^x)$

Réponse: $ −0.2535,$exact :$ 0$

35) La solution$ y′=y^2\ln(x+1),\quad y(0)=1.$ exacte est$ y=−\dfrac{1}{(x+1)(\ln(x+1)−1)}$

36) La solution$ y′=2^x,\quad y(0)=0.$ exacte est$ y=\dfrac{2^x−1}{\ln 2}$

Réponse: $ 1.345,$exact :$ \frac{1}{\ln(2)}$

37) La solution$ y′=y,\quad y(0)=−1.$ exacte est$ y=−e^x$.

38) La solution$ y′=−5t,\quad y(0)=−2.$ exacte est$ y=−\frac{5}{2}t^2−2$

Réponse: $ −4,$exact :$ −1/2$

Des équations différentielles peuvent être utilisées pour modéliser les épidémies de maladies. Dans la série de problèmes suivante, nous examinons l'évolution de la taille de deux sous-populations de personnes vivant dans une ville : les personnes infectées et les personnes susceptibles de l'être. $ S$représente la taille de la population sensible et$ I$ représente la taille de la population infectée. Nous supposons que si une personne sensible interagit avec une personne infectée, il y a une probabilité$ c$ que cette personne soit infectée. Chaque personne infectée se rétablit de l'infection à un rythme$ r$ donné et redevient vulnérable. Nous prenons le cas de la grippe, où nous supposons que personne ne meurt des suites de la maladie. Nous supposons donc que la taille totale de la population des deux sous-populations est constante$ N$. Les équations différentielles qui modélisent ces tailles de population sont

$ S'=rI−cSI$et$ I'=cSI−rI.$

Voici$ c$ le taux de contact et$ r$ le taux de récupération.

39) Montrez que, en supposant que la taille totale de la population est constante,$ (S+I=N),$ vous pouvez réduire le système à une seule équation différentielle dans$ I:I'=c(N−I)I−rI.$

40) En supposant que les paramètres sont$ c=0.5,N=5,$ et$ r=0.5$, dessinez le champ directionnel résultant.

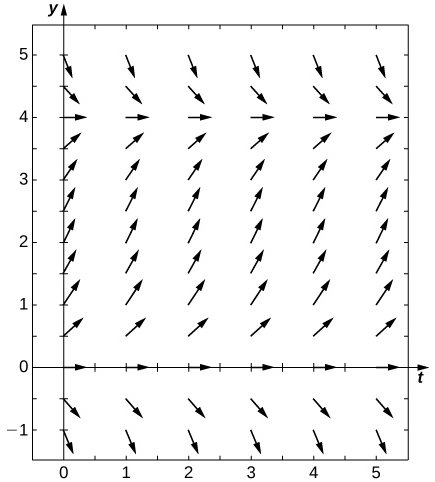
Réponse: $Un champ de direction avec des flèches horizontales pointant vers la droite sur l'axe x et sur y = 4. Les flèches situées sous l'axe x et au-dessus de y = 4 pointent vers le bas et vers la droite. Les flèches entre l'axe x et y = 4 pointent vers le haut et vers la droite.$

41) [T] Utilisez un logiciel de calcul ou une calculatrice pour calculer la solution au problème de valeur initiale$ y'=ty,y(0)=2$ en utilisant la méthode d'Euler avec la taille de pas donnée$ h$. Trouvez la solution sur$ t=1$. Pour un indice, voici un « pseudo-code » expliquant comment écrire un programme informatique pour exécuter la méthode d'Euler pour$ y'=f(t,y),y(0)=2:$

Créer une fonction$ f(t,y)$

Définissez les paramètres$ h$, la taille des$ y(1)=y_0,t(0)=0,$ étapes et le nombre total d'étapes,$ N$

Écrivez une boucle pour :

$ k=1$pour$ N$

$ fn=f(t(k),y(k))$

$ y(k+1)=y(k)+h*fn$

$ t(k+1)=t(k)+h$

42) Résolvez le problème de la valeur initiale pour obtenir la solution exacte.

Réponse: $ y'=2e^{t^2/2}$

43) Dessine le champ directionnel

44)$ h=1$

Réponse: $ 2$

45) [T]$ h=10$

46) [T]$ h=100$

Réponse: $ 3.2756$

47) [T]$ h=1000$

48) [T] Évaluez la solution exacte à$ t=1$. Créez un tableau des erreurs pour l'erreur relative entre la solution de la méthode d'Euler et la solution exacte. Dans quelle mesure l'erreur change-t-elle ? Tu peux m'expliquer ?

Réponse

Solution exacte : y =$ 2\sqrt{e}.$

Taille de l'étape	Erreur
$ h=1$	$ 0.3935$
$ h=10$	$ 0.06163$
$ h=100$	$ 0.006612$
$ h=10000$	$ 0.0006661$

Pour les exercices 49 à 53, considérez le problème de la valeur initiale$ y'=−2y,$ avec$y(0)=2.$

49) Montrez que cela$ y=2e^{−2x}$ résout ce problème de valeur initiale.

50) Dessinez le champ directionnel de cette équation différentielle.

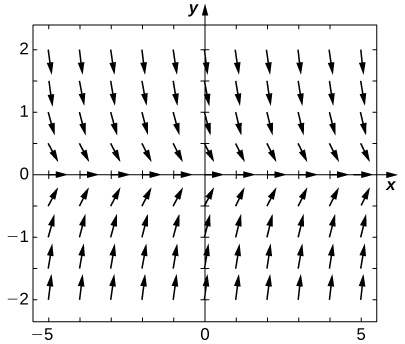
Réponse: $Champ de direction pour l'équation différentielle y' = -2y. Champ de direction avec des flèches horizontales pointant vers la droite sur l'axe X. Au-dessus de l'axe X, les flèches pointent vers le bas et vers la droite. En dessous de l'axe X, les flèches pointent vers le haut et vers la droite. Plus les flèches sont proches de l'axe X, plus elles sont horizontales et plus elles sont éloignées de l'axe X, plus les flèches sont verticales.$

51) [T] À la main, à l'aide d'une calculatrice ou d'un ordinateur, approximez la solution en utilisant la méthode$ t=10$ d'Euler$ h=5$.

52) [T] À l'aide d'une calculatrice ou d'un ordinateur, approximez la solution en utilisant la méthode$ t=10$ d'Euler$ h=100.$

Réponse: $ 4.0741e^{−10}$

53) [T] Tracez la réponse exacte et chaque approximation d'Euler (pour$ h=5$ et$ h=100$) à chaque h sur le champ directionnel. Qu'est-ce que tu remarques ?

Taille de l'étape	Erreur
\( h=1\)	\( 0.3935\)
\( h=10\)	\( 0.06163\)
\( h=100\)	\( 0.006612\)
\( h=10000\)	\( 0.0006661\)