8.2 : Champs de direction et méthodes numériques

Last updated
Save as PDF

Page ID: 197463

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Tracez le champ de direction pour une équation différentielle du premier ordre donnée.
Utilisez un champ de direction pour dessiner une courbe de solution d'une équation différentielle du premier ordre.
Utilisez la méthode d'Euler pour approximer la solution à une équation différentielle du premier ordre.

Pour la suite de ce chapitre, nous allons nous concentrer sur différentes méthodes pour résoudre des équations différentielles et analyser le comportement des solutions. Dans certains cas, il est possible de prédire les propriétés d'une solution à une équation différentielle sans connaître la solution réelle. Nous étudierons également des méthodes numériques pour résoudre des équations différentielles, qui peuvent être programmées à l'aide de différents langages informatiques ou même à l'aide d'un tableur tel que Microsoft Excel.

Création de champs de direction

Les champs de direction (également appelés champs de pente) sont utiles pour étudier les équations différentielles du premier ordre. En particulier, nous considérons une équation différentielle du premier ordre de la forme

\[ y'=f(x,y).\nonumber \]

Un exemple appliqué de ce type d'équation différentielle apparaît dans la loi de Newton sur le refroidissement, que nous allons résoudre de manière explicite plus loin dans ce chapitre. Mais d'abord, créons un champ de direction pour l'équation différentielle

\[ T′(t)=−0.4(T−72).\nonumber \]

Ici$ T(t)$ représente la température (en degrés Fahrenheit) d'un objet à la fois$ t$, et la température ambiante est de$ 72°F$. La figure$ \PageIndex{1}$ montre le champ de direction de cette équation.

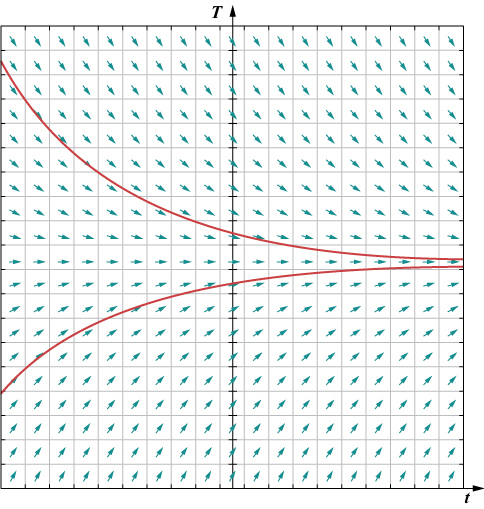
Un graphique d'un champ directionnel pour l'équation différentielle donnée en quadrants un et deux. Les flèches pointent directement vers la droite à y = 72. En dessous de cette ligne, les flèches ont une pente de plus en plus positive à mesure que y diminue. Au-dessus de cette ligne, les flèches ont une pente de plus en plus négative à mesure que y augmente. Les flèches indiquent une convergence à y = 72. Deux solutions sont proposées : une pour une température initiale inférieure à 72 et une pour des températures initiales supérieures à 72. La solution supérieure est une courbe ascendante concave décroissante, approchant y = 72 lorsque t passe à l'infini. La solution inférieure est une courbe descendante concave croissante, approchant y = 72 lorsque t passe à l'infini. — Figure$ \PageIndex{1}$ : Champ de direction pour l'équation différentielle$ T′(t)=−0.4(T−72)$. Deux solutions sont tracées : l'une avec une température initiale inférieure à$ 72°F$ et l'autre avec une température initiale supérieure à$ 72°F$.

L'idée qui sous-tend un champ de direction est le fait que la dérivée d'une fonction évaluée à un point donné est la pente de la tangente au graphe de cette fonction au même point. D'autres exemples d'équations différentielles pour lesquelles nous pouvons créer un champ de direction incluent

\[ y'=3x+2y−4\nonumber \]

\[ y'=x^2−y^2\nonumber \]

\[ y'=\frac{2x+4}{y−2}.\nonumber \]

Pour créer un champ de direction, nous commençons par la première équation :$ y'=3x+2y−4$. Nous utilisons$ \left(x_0,\, y_0\right)$ n'importe quelle paire ordonnée, et nous substituons ces nombres dans la partie droite de l'équation différentielle. Par exemple, si nous choisissons$ x=1$ et$ y=2$, en le remplaçant dans la partie droite de l'équation différentielle, nous obtenons

$ y′=3x+2y−4=3(1)+2(2)−4=3.$

Cela nous indique que si une solution à l'équation différentielle$ y'=3x+2y−4$ passe par le point$ (1,2)$, alors la pente de la solution à ce point doit être égale à 3. Pour commencer à créer le champ de direction, nous plaçons un segment de ligne courte au point$ (1,2)$ incliné$ 3$. Nous pouvons le faire pour n'importe quel point du domaine de la fonction$ f(x,y)=3x+2y−4,$ qui comprend toutes les paires ordonnées$ (x,y)$ dans$ R^2$. Par conséquent, chaque point du plan cartésien est associé à une pente, en supposant qu'une solution à l'équation différentielle passe par ce point. Le champ de direction de l'équation différentielle$ y′=3x+2y−4$ est illustré sur la figure$ \PageIndex{2}$.

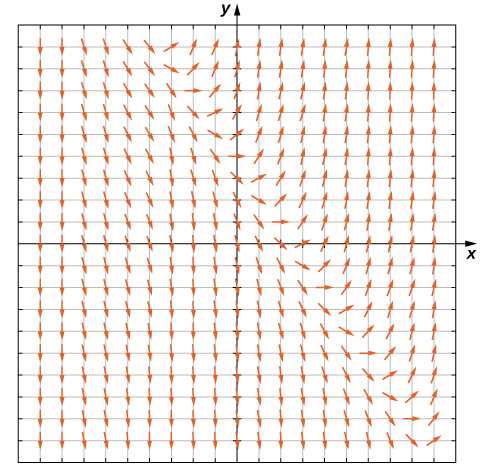
Un graphique du champ de direction pour l'équation différentielle y' = 3 x + 2 y — 4 dans les quatre quadrants. Dans les quadrants deux et trois, les flèches pointent vers le bas et légèrement vers la droite. Sur une ligne diagonale, approximativement y = -x + 2, les flèches pointent de plus en plus vers la droite, se courbent, puis pointent vers le haut au-dessus de cette ligne. — Figure$ \PageIndex{2}$ : Champ de direction pour l'équation différentielle$ y'=3x+2y−4$.

Nous pouvons générer un champ de direction de ce type pour n'importe quelle équation différentielle de la forme$ y'=f(x,y).$

Définition : Champ de direction (champ de pente)

Un champ de direction (champ de pente) est un objet mathématique utilisé pour représenter graphiquement les solutions à une équation différentielle du premier ordre. À chaque point d'un champ de direction, apparaît un segment de droite dont la pente est égale à la pente d'une solution à l'équation différentielle passant par ce point.

Utilisation des champs de direction

Nous pouvons utiliser un champ de direction pour prédire le comportement des solutions à une équation différentielle sans connaître la solution réelle. Par exemple, le champ de direction de la figure$ \PageIndex{3}$ sert de guide pour le comportement des solutions à l'équation différentielle$ y'=3x+2y−4.$

Pour utiliser un champ de direction, nous commençons par sélectionner n'importe quel point du champ. Le segment de ligne à ce point sert de panneau indicateur nous indiquant la direction à prendre à partir de là. Par exemple, si une solution à l'équation différentielle passe par le point$ (0,1),$, alors la pente de la solution passant par ce point est donnée par$ y'=3(0)+2(1)−4=−2.$ Maintenant,$ x$ augmentez légèrement, disons à$ x=0.1$. L'utilisation de la méthode des approximations linéaires donne une formule pour la valeur approximative de$ y$ pour$ x=0.1.$ En particulier,

\[ L(x)=y_0+f′(x_0)(x−x_0)=1−2(x_0−0)=1−2x_0.\nonumber \]

La substitution$ x_0=0.1$ par$ L(x)$ donne une$ y$ valeur approximative de$ 0.8$.

À ce stade, la pente de la solution change (toujours selon l'équation différentielle). Nous pouvons continuer à progresser, en recalculant la pente de la solution au fur et à mesure que nous faisons de petits pas vers la droite et en surveillant le comportement de la solution. La figure$ \PageIndex{3}$ montre un graphique de la solution passant par le point$ (0,1)$.

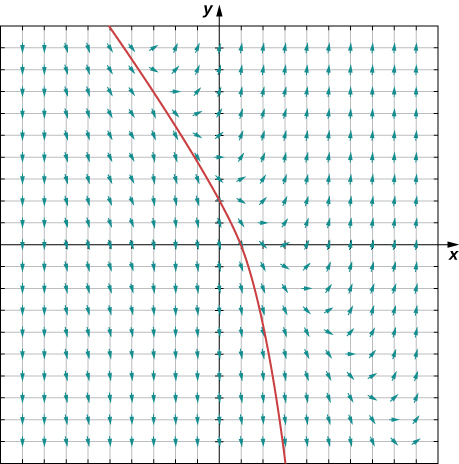
La courbe est le graphique de la solution au problème de la valeur initiale

\[ y'=3x+2y−4,\; y(0)=1.\nonumber \]

Cette courbe est appelée courbe de solution passant par le point.$ (0,1).$ La solution exacte à ce problème de valeur initiale est

\[ y=−\frac{3}{2}x+\frac{5}{4}−\frac{1}{4}e^{2x},\nonumber \]

et le graphique de cette solution est identique à la courbe de la figure$ \PageIndex{3}$.

Exercice$\PageIndex{1}$

Créez un champ de direction pour l'équation différentielle$ y'=x^2−y^2$ et esquissez une courbe de solution passant par le point$ (−1,2)$.

Allusion: Utilisation$ x$ et$ y$ valeurs comprises entre$ −5$ et$ 5$. Pour chaque paire de coordonnées, calculez$ y'$ en utilisant la partie droite de l'équation différentielle.

Réponse: $Un graphique du champ de direction pour l'équation différentielle y' = x ^ 2 — y ^ 2. Le long de y = x et y = -x, les lignes sont horizontales. De chaque côté de y = x et y = -x, les lignes inclinent et orientent les solutions le long de ces deux fonctions. Le reste des lignes est vertical. La solution passant par (-1, 2) est affichée. Il courbe vers le bas d'environ (-2,75, 10), en passant par (-1, 2) et environ (0, 1,5), puis vers le haut le long de la diagonale jusqu'à (10, 10).$

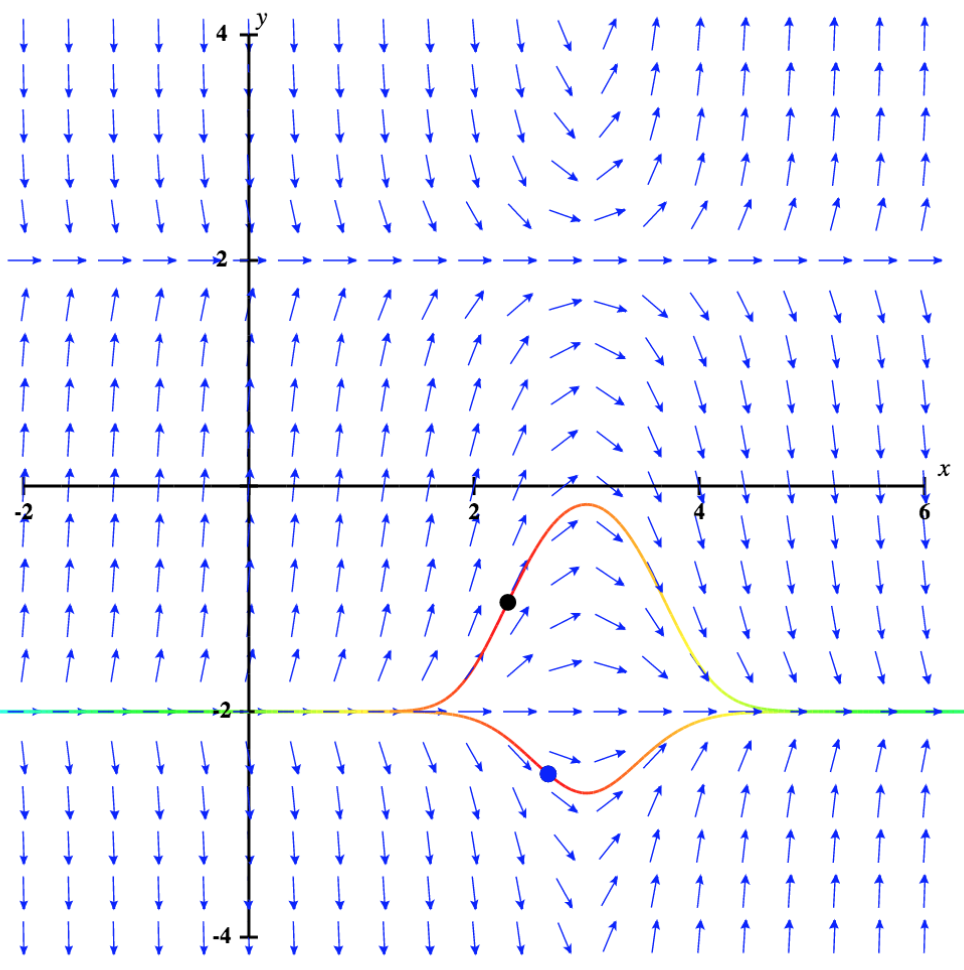
Considérons maintenant le champ de direction de l'équation différentielle$ y'=(x−3)(y^2−4)$, illustré sur la figure$ \PageIndex{4}$. Ce champ de direction possède plusieurs propriétés intéressantes. Tout d'abord, à$ y=−2$ et$ y=2$, des tirets horizontaux apparaissent sur tout le graphique. Cela signifie que si$ y=−2$, alors la$ y'=0.$ substitution de cette expression dans le côté droit de l'équation différentielle donne

\ [\ begin {align*} (x−3) (y^2−4) &= (x−3) ((−2) ^2−4) \ \ [4 points]
& =( x−3) (0) \ \ [4 points]
&=0 \ \ [4 points]
&=y'. \ end {align*} \]

Il$ y=−2$ s'agit donc d'une solution à l'équation différentielle. De même,$ y=2$ est une solution à l'équation différentielle. Ce sont les seules solutions à valeur constante à l'équation différentielle, comme le montre l'argument suivant. Supposons qu'$ y=k$il s'agisse d'une solution constante à l'équation différentielle. Alors$ y′=0$. La substitution de cette expression dans l'équation différentielle donne des résultats$ 0=(x−3)(k^2−4)$. Cette équation doit être vraie pour toutes les valeurs de$ x$, de sorte que le deuxième facteur doit être égal à zéro. Ce résultat donne l'équation$ k^2−4=0$. Les solutions à cette équation sont$ k=−2$ et$ k=2$, qui sont les solutions constantes déjà mentionnées. C'est ce que l'on appelle les solutions d'équilibre de l'équation différentielle.

Un champ de direction pour l'équation différentielle donnée. Les flèches sont horizontales et pointent vers la droite sur y = -2, y = 2 et x = 3. Plus les flèches sont proches de x = 6, plus elles deviennent horizontales. Plus ils sont éloignés, plus ils sont verticaux. — Figure$ \PageIndex{4}$ : Champ de direction pour l'équation différentielle$ y'=(x−3)(y^2−4)$ montrant deux solutions. Ces solutions sont très proches les unes des autres, mais l'une se situe à peine au-dessus de la solution d'équilibre$ x=−2$ et l'autre à peine en dessous de la même solution d'équilibre.

Définition : Solutions d'équilibre

Considérez l'équation différentielle$ y'=f(x,y)$. Une solution d'équilibre est n'importe quelle solution à l'équation différentielle de la forme$ y=c$, où$c$ est une constante.

Pour déterminer les solutions d'équilibre de l'équation différentielle$ y'=f(x,y)$, réglez le côté droit sur zéro. Une solution d'équilibre de l'équation différentielle est une fonction de la forme$ y=k$ telle que$ f(x,k)=0$ pour toutes les valeurs de$ x$ dans le domaine de$ f$.

Une caractéristique importante des solutions d'équilibre concerne le fait qu'elles s'approchent ou non de la droite$ y=k$ en tant qu'asymptote pour des valeurs élevées de$ x$.

Définition : solutions asymptotiquement stables, instables et semi-stables

Examinez l'équation différentielle$ y′=f(x,y),$ et supposez que toutes les solutions à cette équation différentielle sont définies pour$ x≥x_0$. $ y=k$Soyons une solution d'équilibre à l'équation différentielle.

$ y=k$est une solution asymptotiquement stable à l'équation différentielle s'il existe une$ ε>0$ telle solution que, pour n'importe quelle valeur,$ c∈(k−ε,\, k+ε)$ la solution au problème des valeurs initiales se$ y′=f(x,y), \; y(x_0)=c$$ x$ rapproche$ k$ de l'infini.
$ y=k$est une solution asymptotiquement instable à l'équation différentielle s'il existe une$ ε>0$ telle solution que, pour n'importe quelle valeur,$ c∈(k−ε,\, k+ε)$ la solution au problème de la valeur initiale ne se rapproche$ y′=f(x,y), \; y(x_0)=c$$ k$ jamais de l'infini.$ x$
$ y=k$est une solution asymptotiquement semi-stable à l'équation différentielle si elle n'est ni asymptotiquement stable ni asymptotiquement instable.

Revenons maintenant à l'équation différentielle$ y'=(x−3)(y^2−4)$, avec la condition initiale$ y(0)=0.5$. Le champ de direction de ce problème de valeur initiale, ainsi que la solution correspondante, sont illustrés sur la figure$ \PageIndex{5}$.

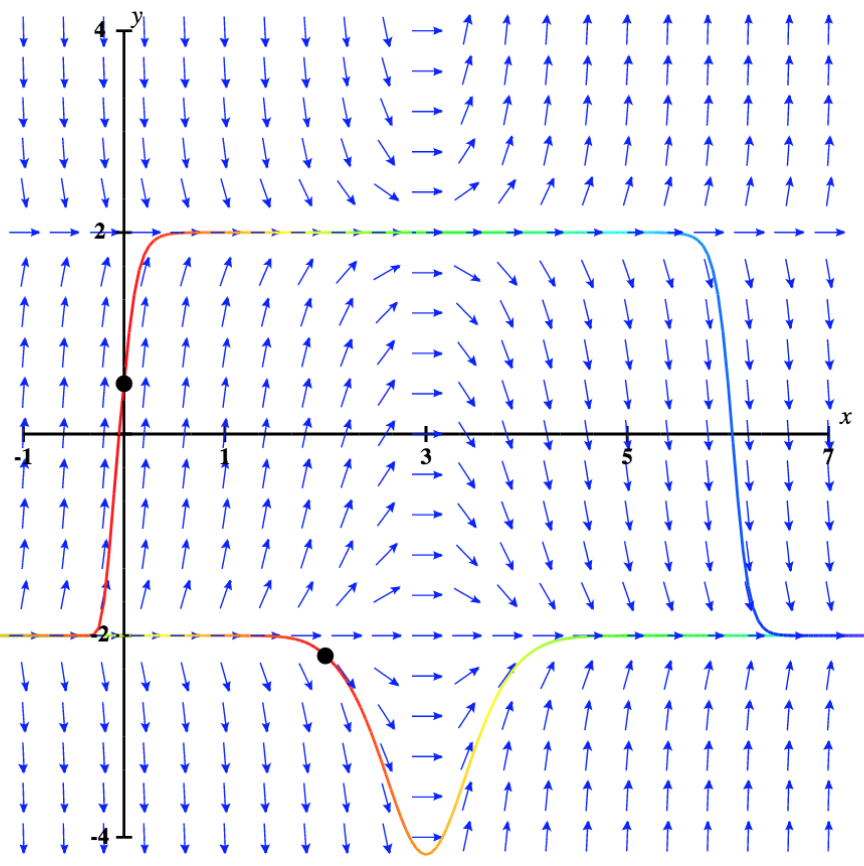
Un champ de direction pour l'équation différentielle donnée. Les flèches sont horizontales et pointent vers la droite sur y = -2, y = 2 et x = 3. Une solution est représentée graphiquement qui passe par (0, 0,5) et une autre par le point (2, -2,2). Les deux courbes se rapprochent finalement de la droite y = -2 de manière asymptotique. — Figure$ \PageIndex{5}$ : Champ de direction pour le problème de valeur initiale$ y'=(x−3)(y^2−4),\; y(0)=0.5.$ Une deuxième courbe de solution est représentée graphiquement avec la condition initiale$(2, -2.2)$.

Les valeurs de la solution à ce problème de valeur initiale restent comprises entre$ y=−2$ et$ y=2$, qui sont les solutions d'équilibre de l'équation différentielle. De plus, à mesure que l'on s'$ x$approche de l'infini, bien qu'elles semblent initialement s'approcher de la ligne y = 2, les$ y$ coordonnées s'approchent clairement$ -2$. Le comportement des solutions est similaire si la valeur initiale est inférieure$ -2$, par exemple,$ y(2)=-2.2$. Dans ce cas, les solutions augmentent et s'approchent à$ y=-2$ mesure que l'infini se$ x$ rapproche. Il$ y=-2$ s'agit donc d'une solution asymptotiquement stable à cette équation différentielle.

Que se passe-t-il lorsque la valeur initiale est supérieure$ y=2$ ? Ce scénario est illustré sur la figure$ \PageIndex{6}$, avec la valeur initiale$ y(0)=3.$

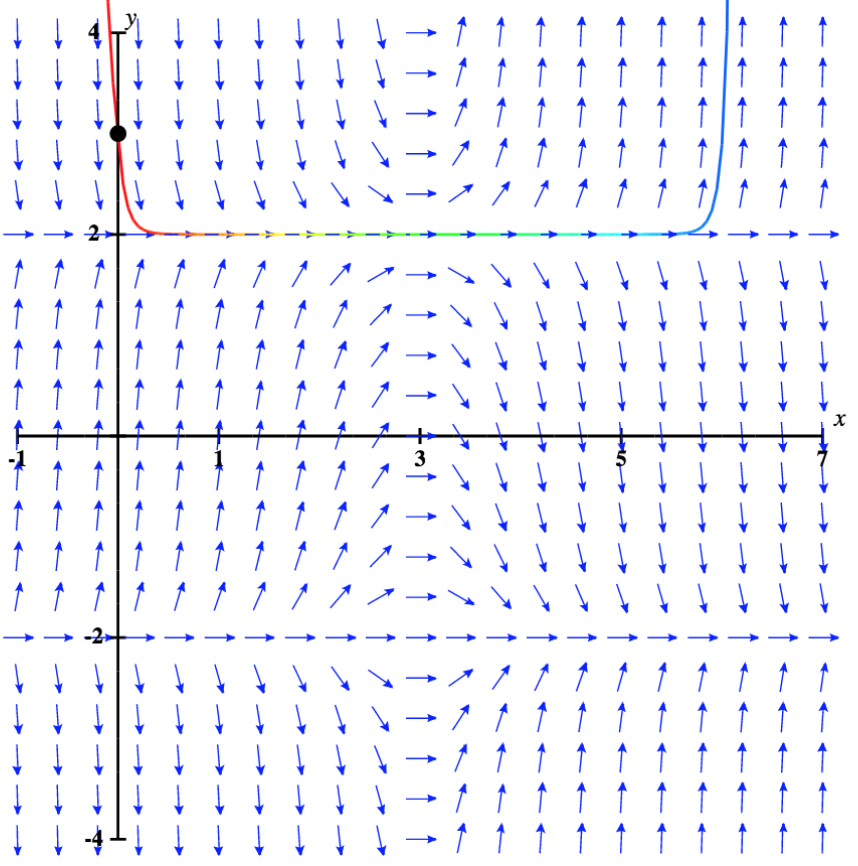
La solution augmente rapidement vers l'infini positif à mesure que l'on$ x$ approche de l'infini De plus, si la valeur initiale est légèrement inférieure$ 2$, alors la solution approche$ -2$, qui est l'autre solution d'équilibre. Par conséquent, dans aucun des cas$ y=2$, la solution ne$ y=2$ s'approche ; on parle donc de solution d'équilibre asymptotiquement instable ou instable.

Exemple$ \PageIndex{1}$: Stability of an Equilibrium Solution

Créez un champ de direction pour l'équation différentielle$ y'=(y−3)^2(y^2+y−2)$ et identifiez toutes les solutions d'équilibre. Classez chacune des solutions d'équilibre comme étant stable, instable ou semi-stable.

Solution

Le champ de direction est illustré sur la figure$ \PageIndex{7}$.

Un graphique d'un champ de direction avec des flèches pointant vers la droite sur y = -4, y = 2 et y = 6. Pour y < -4, les flèches pointent vers le haut. Pour -4 < y < 2, les flèches pointent vers le bas. Pour 2 < y <6, les flèches pointent vers le haut et deviennent de plus en plus plates à mesure qu'elles approchent de y = 6. Pour y — Figure$ \PageIndex{7}$ : Champ de direction pour l'équation différentielle$ y'=(y−3)^2(y^2+y−2).$

Les solutions d'équilibre sont$ y=−2,\, y=1,$ et$ y=3$. Pour classer chacune des solutions, regardez une flèche située juste au-dessus ou en dessous de chacune de ces valeurs. Par exemple,$ y=−2$ les flèches situées juste en dessous de cette solution pointent vers le haut et les flèches situées directement au-dessus de la solution pointent vers le bas. Toutes les conditions initiales sont donc proches de$ y=−2$ l'$ y=−2$approche et la solution est stable. Pour la solution$ y=1$, toutes les conditions initiales supérieures et inférieures$ y=1$ sont repoussées (repoussées)$ y=1$, de sorte que cette solution est instable. La solution$ y=3$ est semi-stable, car pour des conditions initiales légèrement supérieures à$ 3$, la solution se rapproche de l'infini, et pour des conditions initiales légèrement inférieures à$ 3$, la solution se rapproche$ y=1$.

Analyse

Il est possible de trouver les solutions d'équilibre à l'équation différentielle en réglant le côté droit à zéro et en résolvant pour$ y.$ Cette approche donne les mêmes solutions d'équilibre que celles que nous avons vues dans le champ de direction.

Exercice$\PageIndex{2}$

Créez un champ de direction pour l'équation différentielle$ y'=(x+5)(y+2)(y^2−4y+4)$ et identifiez toutes les solutions d'équilibre. Classez chacune des solutions d'équilibre comme étant stable, instable ou semi-stable.

Allusion: Créez d'abord le champ de direction et recherchez les tirets horizontaux transversaux. Examinez ensuite les lignes de pente directement au-dessus et en dessous des solutions d'équilibre.

Réponse

Les solutions d'équilibre sont$ y=−2$ et$ y=2$. Pour cette équation,$ y=−2$ est une solution d'équilibre instable et$ y=2$ est une solution d'équilibre semi-stable.

Un champ de direction avec des flèches pointant vers la droite sur y = -4 et y = 4. Les flèches pointent vers le haut pour y -4 et vers le bas pour y < -4. Près de y = 4, les flèches sont plus horizontales, mais plus elles s'éloignent, plus elles deviennent verticales." src="https://math.libretexts.org/@api/dek...2452/8.2.3.png">

Méthode d'Euler

Considérez le problème de la valeur initiale

\[ y′=2x−3,\;y(0)=3.\nonumber \]

L'intégration des deux côtés de l'équation différentielle donne$ y=x^2−3x+C,$ et la résolution pour$ C$ donne la solution particulière.$ y=x^2−3x+3.$ La solution à ce problème de valeur initiale apparaît sous forme de parabole sur la figure$ \PageIndex{8}$.

Un graphique sur la plage [-1,4] pour x et y. La parabole d'ouverture vers le haut donnée est dessinée avec le sommet à (1,5, 0,75). Les points individuels sont tracés en (0, 3), (0,5, 1,5), (1, 0,5), (1,5, 0), (2, 0), (2,5, 0,5) et (3, 1,5) à l'aide de segments de ligne les reliant. — Figure$ \PageIndex{8}$ : Méthode d'Euler pour le problème de la valeur initiale$ y′=2x−3,y(0)=3.$

Le graphique rouge est constitué de segments de ligne qui donnent une idée approximative de la solution au problème de valeur initiale. Le graphique commence à la même valeur initiale de$ (0,3)$. Ensuite, la pente de la solution en tout point est déterminée par le côté droit de l'équation différentielle, et la longueur du segment de droite est déterminée en augmentant la$ x$ valeur à$ 0.5$ chaque fois (la taille du pas). Cette approche est à la base de la méthode d'Euler.

Avant d'énoncer la méthode d'Euler en tant que théorème, examinons un autre problème de valeur initiale :

\[ y′=x^2−y^2,\; y(−1)=2.\nonumber \]

L'idée sous-jacente aux champs de direction peut également être appliquée à ce problème pour étudier le comportement de sa solution. Par exemple, au point par$ (−1,2),$ lequel la pente de la solution est donnée$ y'=(−1)^2−2^2=−3$, la pente de la tangente à la solution à ce point est également égale à$ −3$. Maintenant, nous définissons$ x_0=−1$ et$ y_0=2$. Puisque la pente de la solution à ce point est égale à$ −3$, nous pouvons utiliser la méthode d'approximation linéaire pour approximer y à proximité$ (−1,2)$.

\[ L(x)=y_0+f′(x_0)(x−x_0).\nonumber \]

Ici$ x_0=−1,y_0=2,$ et$ f′(x_0)=−3,$ ainsi, l'approximation linéaire devient

\[ L(x)=2−3(x−(−1))=2−3x−3=−3x−1.\nonumber \]

Nous choisissons maintenant une taille de marche. La taille de l'étape est une petite valeur, généralement inférieure$ 0.1$ ou égale à, qui sert d'incrément à$ x$ ; elle est représentée par la variable$ h$. Dans notre exemple, laissons$ h=0.1$. L'incrémentation$ x_0$ de$ h$ donne notre$ x$ valeur suivante :

\[ x_1=x_0+h=−1+0.1=−0.9.\nonumber \]

Nous pouvons la$ x_1=−0.9$ remplacer par l'approximation linéaire à calculer$ y_1$.

\[ y_1=L(x_1)=−3(−0.9)−1=1.7.\nonumber \]

Par conséquent, la$ y$ valeur approximative de la solution quand$ x=−0.9$ est$ y=1.7$. Nous pouvons ensuite répéter le processus, en utilisant$ x_1=−0.9$ et$ y_1=1.7$ pour calculer$ x_2$ et$ y_2$. La nouvelle pente est donnée par$ y'=(−0.9)^2−(1.7)^2=−2.08.$ First,$ x_2=x_1+h=−0.9+0.1=−0.8.$ l'utilisation d'une approximation linéaire donne

\ (\ begin {align*} L (x) &=y_1+f′ (x_1) (x−x_1) \ \ [4 points]
&=1,7−2,08 (x− (−0,9)) \ \ [4 points]
&=1,7−2,08x−1,872 \ \ [4 points] &=−2,08x−0,172 \ \ [4 points]
&=−2,08 x −0,172. \ end {align*} \)

Enfin, nous la$ x_2=−0.8$ substituons à l'approximation linéaire à calculer$ y_2$.

\ (\ begin {align*} Y_2&=L (x_2) \ \ [4 points]
&=−2,08x_2−0,172 \ \ [4 points]
&=−2,08 (−0,8) −0,172 \ \ [4 points]
&=1,492. \ end {align*} \)

Par conséquent, la valeur approximative de la solution à l'équation différentielle est$ y=1.492$ lorsque$ x=−0.8.$

Ce que nous venons de montrer, c'est l'idée qui sous-tend la méthode d'Euler. La répétition de ces étapes permet d'obtenir une liste de valeurs pour la solution. Ces valeurs sont présentées dans le tableau, arrondies à la quatrième décimale.

Tableau$ \PageIndex{1}$ : Utilisation de la méthode d'Euler pour approximer les solutions d'une équation différentielle
$ n$	0	1	2	3	4	5
$ x_n$	−1	−0,9	−0,8	−0,7	−0,6	−0,5
$ y_n$	2	1,7	1,492	1,334	1 2046	1 095
$ n$	6	7	8	9	10
$ x_n$	−0,4	−0,3	−0,2	−0,1	0
$ y_n$	1 0004	1,9164	1.8414	1,746	1,7 156

Méthode d'Euler

Considérez le problème de la valeur initiale

\[ y'=f(x,y),\; y(x_0)=y_0.\nonumber \]

Pour trouver une solution approximative à ce problème à l'aide de la méthode d'Euler, définissez

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$.

$ h>0$Représente ici la taille de l'étape et$ n$ est un entier, commençant par$ 1$. Le nombre de pas effectués est compté par la variable$ n$.

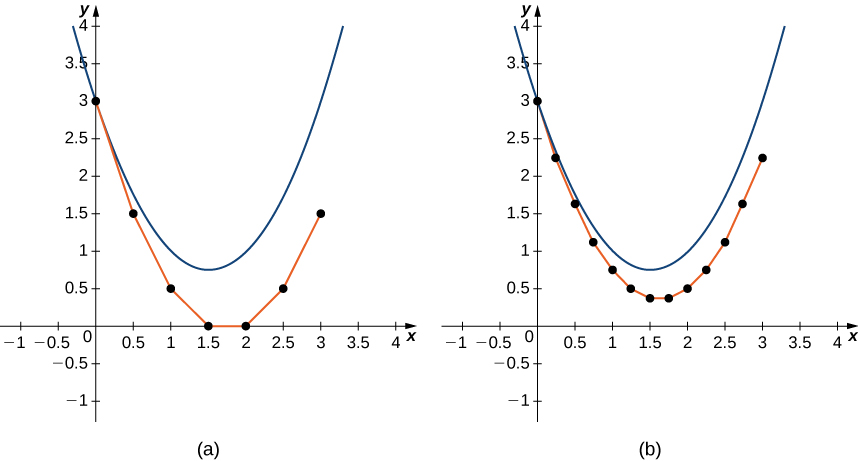
$ h$Il s'agit généralement d'une petite valeur, disons$ 0.1$ ou$ 0.05$. Plus la valeur de est faible$ h$, plus les calculs sont nécessaires. Plus la valeur de est élevée$ h$, moins de calculs sont nécessaires. Cependant, le compromis se traduit par un degré de précision plus faible pour une plus grande taille de pas, comme illustré à la figure$ \PageIndex{9}$.

Deux graphes de la même parabole, y = x ^ 2 — 3 x + 3. La première montre la méthode d'Euler pour le problème de valeur initiale donné avec une taille de pas de h = 0,05, et la seconde montre la méthode d'Euler avec une taille de pas de h = 0,25. Dans le premier cas, les points (0, 3), (0,5, 1,5), (1, 0,5), (1,5, 0), (2, 0), (2,5, 0,5) et (3, 1,5) sont tracés par des segments de ligne les reliant. Le second comporte les points (0, 3), (0,25, 2,25), (0,5, 1,625), (0,75, 1,125), (1, 0,75), (1,25, 0,5), (1,5, 0,375), (2, 0,5), (2,25, 0,75), (2,5, 1,125), (2,75, 1,625) et (3, 2,25) tracés avec des segments de ligne en les connectant. — Figure$ \PageIndex{9}$ : Méthode d'Euler pour le problème de la valeur initiale$ y′=2x−3,\; y(0)=3$ avec (a) un pas de$ h=0.5$ ; et (b) un pas de$ h=0.25.$

Exemple$ \PageIndex{2}$: Using Euler’s Method

Considérez le problème de la valeur initiale

\[ y′=3x^2−y^2+1,\; y(0)=2.\nonumber \]

Utilisez la méthode d'Euler avec une taille d'étape de$ 0.1$ pour générer un tableau de valeurs pour la solution pour les valeurs comprises$ x$ entre$ 0$ et$ 1$.

Solution

Nous sommes donnés$ h=0.1$ et en$ f(x,y)=3x^2−y^2+1.$ outre, la condition initiale$ y(0)=2$ donne$ x_0=0$ et$ y_0=2$. En utilisant l'équation avec$ n=0$, nous pouvons générer cette table.

Tableau$ \PageIndex{2}$ : Utilisation de la méthode d'Euler pour approximer les solutions d'une équation différentielle
$ n$	$ x_n$	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
\ (n \) » style="vertical-align:middle ; « >0	\ (x_n \) » style="vertical-align:middle ; « >0	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="vertical-align:middle ; « >2
\ (n \) » style="vertical-align:middle ; « >1	\ (x_n \) » style="vertical-align:middle ; « >0,1	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_1=y_0+hf(x_0,y_0)=1.7$
\ (n \) » style="vertical-align:middle ; « >2	\ (x_n \) » style="vertical-align:middle ; « >0,2	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_2=y_1+hf(x_1,y_1)=1.514$
\ (n \) » style="vertical-align:middle ; « >3	\ (x_n \) » style="vertical-align:middle ; « >0,3	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_3=y_2+hf(x_2,y_2)=1.3968$
\ (n \) » style="vertical-align:middle ; « >4	\ (x_n \) » style="vertical-align:middle ; « >0.4	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_4=y_3+hf(x_3,y_3)=1.3287$
\ (n \) » style="vertical-align:middle ; « >5	\ (x_n \) » style="vertical-align:middle ; « >0,5	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_5=y_4+hf(x_4,y_4)=1.3001$
\ (n \) » style="vertical-align:middle ; « >6	\ (x_n \) » style="vertical-align:middle ; « >0,6	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_6=y_5+hf(x_5,y_5)=1.3061$
\ (n \) » style="vertical-align:middle ; « >7	\ (x_n \) » style="vertical-align:middle ; « >0.7	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_7=y_6+hf(x_6,y_6)=1.3435$
\ (n \) » style="vertical-align:middle ; « >8	\ (x_n \) » style="vertical-align:middle ; « >0,8	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_8=y_7+hf(x_7,y_7)=1.4100$
\ (n \) » style="vertical-align:middle ; « >9	\ (x_n \) » style="vertical-align:middle ; « >0,9	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_9=y_8+hf(x_8,y_8)=1.5032$
\ (n \) » style="vertical-align:middle ; « >10	\ (x_n \) » style="vertical-align:middle ; « >1.0	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1}) \) » style="align-vertical:middle ; « >$ y_{10}=y_9+hf(x_9,y_9)=1.6202$

Avec dix calculs, nous sommes en mesure d'approximer les valeurs de la solution au problème de valeur initiale pour des valeurs comprises$ x$ entre$ 0$ et$ 1$.

Visitez ce site Web pour découvrir visuellement la méthode d'Euler.

Exercice$\PageIndex{3}$

Considérez le problème de la valeur initiale

\[ y′=x^3+y^2,\; y(1)=−2.\nonumber \]

En utilisant une taille de pas de$ 0.1$, générez un tableau avec des valeurs approximatives pour résoudre le problème de valeur initiale pour les valeurs comprises$ x$ entre$ 1$ et$ 2$.

Allusion: Commencez par identifier la valeur de$ h$, puis déterminez ce qui$ f(x,y)$ est. Utilisez ensuite la formule de la méthode d'Euler pour calculer$ y_1,y_2,$ et ainsi de suite.

Réponse

Tableau$ \PageIndex{3}$ : Utilisation de la méthode d'Euler pour approximer les solutions à l'équation différentielle dans l'exercice$\PageIndex{3}$.
$ n$	\ (x_n)	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
0	1	−2
1	1.1	$ y_1=y_0+hf(x_0,y_0)=−1.5$
2	1.2	$ y_2=y_1+hf(x_1,y_1)=−1.1419$
3	1.3	$ y_3=y_2+hf(x_2,y_2)=−0.8387$
4	1.4	$ y_4=y_3+hf(x_3,y_3)=−0.5487$
5	1,5	$ y_5=y_4+hf(x_4,y_4)=−0.2442$
6	1,6	$ y_6=y_5+hf(x_5,y_5)=0.0993$
7	1,7	$ y_7=y_6+hf(x_6,y_6)=0.5099$
8	1,8	$ y_8=y_7+hf(x_7,y_7)=1.0272$
9	1,9	$ y_9=y_8+hf(x_8,y_8)=1.7159$
10	2	$ y_{10}=y_9+hf(x_9,y_9)=2.6962$

Concepts clés

Un champ de direction est un objet mathématique utilisé pour représenter graphiquement les solutions à une équation différentielle du premier ordre.
La méthode d'Euler est une technique numérique qui peut être utilisée pour approximer les solutions d'une équation différentielle.

Équations clés

Méthode d'Euler

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$, où$ h$ est la taille du pas

Lexique

solution semi-stable asymptotiquement: $ y=k$s'il n'est ni asymptotiquement stable ni asymptotiquement instable

solution asymptotiquement stable: $ y=k$s'il existe$ ε>0$ une solution telle que, pour une valeur quelconque,$ c∈(k−ε,\, k+ε)$ la solution au problème de la valeur initiale se$ y′=f(x,y),\; y(x_0)=c$$ x$ rapproche$ k$ de l'infini

solution asymptotiquement instable: $ y=k$s'il existe une solution$ ε>0$ telle que, pour quelque valeur que ce soit,$ c∈(k−ε,\, k+ε)$ la solution au problème de la valeur initiale$ y′=f(x,y),\; y(x_0)=c$ ne s'approche jamais$ k$ de$ x$ l'infini

champ de direction (champ de pente): un objet mathématique utilisé pour représenter graphiquement les solutions à une équation différentielle du premier ordre ; à chaque point d'un champ de direction apparaît un segment de droite dont la pente est égale à la pente d'une solution à l'équation différentielle passant par ce point

solution d'équilibre: toute solution à l'équation différentielle de la forme$ y=c,$ où$ c$ est une constante

Méthode d'Euler: une technique numérique utilisée pour approximer les solutions à un problème de valeur initiale

courbe de solution: une courbe tracée dans un champ de direction qui correspond à la solution du problème de valeur initiale passant par un point donné du champ de direction

taille du pas: l'incrément hh qui est ajouté à la valeur xx à chaque étape de la méthode d'Euler

Contributeurs et attributions

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) edited this section to adjust the explanation of equilibrium points in the example shown in Figures $ \PageIndex{4}$ - $ \PageIndex{6}$. He also created these figures.

Définition : Champ de direction (champ de pente)

Exercice\(\PageIndex{1}\)

Définition : Solutions d'équilibre

Définition : solutions asymptotiquement stables, instables et semi-stables

Exemple\( \PageIndex{1}\): Stability of an Equilibrium Solution

Exercice\(\PageIndex{2}\)

Méthode d'Euler

Exemple\( \PageIndex{2}\): Using Euler’s Method

Exercice\(\PageIndex{3}\)

\( n\)	0	1	2	3	4	5
\( x_n\)	−1	−0,9	−0,8	−0,7	−0,6	−0,5
\( y_n\)	2	1,7	1,492	1,334	1 2046	1 095
\( n\)	6	7	8	9	10
\( x_n\)	−0,4	−0,3	−0,2	−0,1	0
\( y_n\)	1 0004	1,9164	1.8414	1,746	1,7 156

\( n\)	\ (x_n)	\( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\)
0	1	−2
1	1.1	\( y_1=y_0+hf(x_0,y_0)=−1.5\)
2	1.2	\( y_2=y_1+hf(x_1,y_1)=−1.1419\)
3	1.3	\( y_3=y_2+hf(x_2,y_2)=−0.8387\)
4	1.4	\( y_4=y_3+hf(x_3,y_3)=−0.5487\)
5	1,5	\( y_5=y_4+hf(x_4,y_4)=−0.2442\)
6	1,6	\( y_6=y_5+hf(x_5,y_5)=0.0993\)
7	1,7	\( y_7=y_6+hf(x_6,y_6)=0.5099\)
8	1,8	\( y_8=y_7+hf(x_7,y_7)=1.0272\)
9	1,9	\( y_9=y_8+hf(x_8,y_8)=1.7159\)
10	2	\( y_{10}=y_9+hf(x_9,y_9)=2.6962\)