8.3E : Exercices pour la section 8.3

Last updated
Save as PDF

Page ID: 197455

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Dans les exercices 1 à 4, résolvez les problèmes de valeur initiale suivants avec la condition initiale\( y_0=0\) et représentez la solution sous forme graphique.

1)\( \dfrac{dy}{dt}=y+1\)

Réponse: \( y=e^t−1\)

2)\( \dfrac{dy}{dt}=y−1\)

3)\( \dfrac{dy}{dt}=-y+1\)

Réponse: \( y=1−e^{−t}\)

4)\( \dfrac{dy}{dt}=−y−1\)

Dans les exercices 5 à 14, trouvez la solution générale à l'équation différentielle.

5)\( x^2y'=(x+1)y\)

Réponse: \( y=Cxe^{−1/x}\)

6)\( y'=\tan(y)x\)

7)\( y'=2xy^2\)

Réponse: \( y=\dfrac{1}{C−x^2}\)

8)\( \dfrac{dy}{dt}=y\cos(3t+2)\)

9)\( 2x\dfrac{dy}{dx}=y^2\)

Réponse: \( y=−\dfrac{2}{C+\ln|x|}\)

10)\( y'=e^yx^2\)

11)\( (1+x)y'=(x+2)(y−1)\)

Réponse: \( y=Ce^x(x+1)+1\)

(12)\( \dfrac{dx}{dt}=3t^2(x^2+4)\)

13)\( t\dfrac{dy}{dt}=\sqrt{1−y^2}\)

Réponse: \( y=\sin(\ln|t|+C)\)

(14)\( y'=e^xe^y\)

Dans les exercices 15 à 24, trouvez la solution au problème de la valeur initiale.

(15)\( y'=e^{y−x}, \quad y(0)=0\)

Réponse: \( y=−\ln(e^{−x})\)ce qui simplifie\(y = x\)

16)\( y'=y^2(x+1), \quad y(0)=2\)

17)\( \dfrac{dy}{dx}=y^3xe^{x^2}, \quad y(0)=1\)

Réponse: \( y=\dfrac{1}{\sqrt{2−e^{x^2}}}\)

18)\( \dfrac{dy}{dt}=y^2e^x\sin(3x), \quad y(0)=1\)

19)\( y'=\dfrac{x}{\text{sech}^2y}, \quad y(0)=0\)

Réponse: \( y=\tanh^{−1}\left(\dfrac{x^2}{2}\right)\)

(20)\( y'=2xy(1+2y), \quad y(0)=−1\)

(21)\( \dfrac{dx}{dt}=\ln(t)\sqrt{1−x^2}, \quad x(1)=0\)

Réponse: \( x=\sin(1 - t + t\ln t)\)

(22)\( y'=3x^2(y^2+4),\quad y(0)=0\)

23)\( y'=e^y5^x, \quad y(0)=\ln(\ln(5))\)

Réponse: \( y=\ln(\ln(5))−\ln(2−5^x)\)

(24)\( y'=−2x\tan(y), \quad y(0)=\dfrac{π}{2}\)

Pour les problèmes 25 à 29, utilisez un logiciel ou votre calculatrice pour générer les champs directionnels. Résolvez explicitement et tracez des courbes de solution pour plusieurs conditions initiales. Certaines conditions initiales critiques modifient-elles le comportement de la solution ?

25) [T]\( y'=1−2y\)

Réponse

\( y=Ce^{−2}x+\dfrac{1}{2}\)

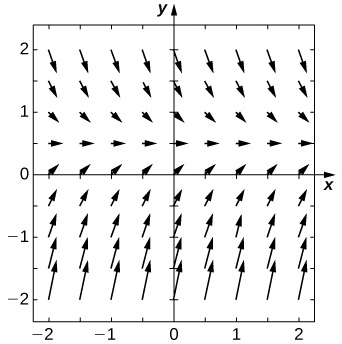
26) [T]\( y'=y^2x^3\)

27) [T]\( y'=y^3e^x\)

Réponse

\( y=\dfrac{1}{\sqrt{2}\sqrt{C−e^x}}\)

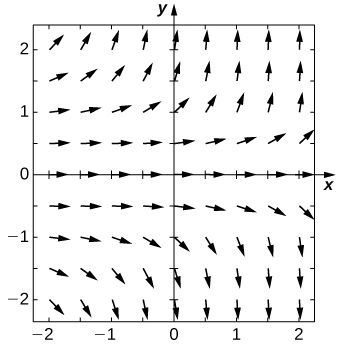
28) [T]\( y'=e^y\)

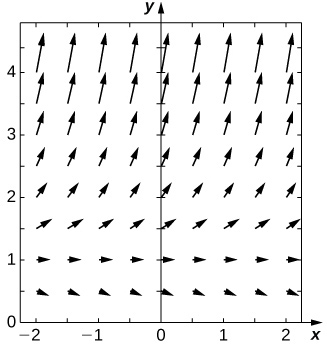
29) [T]\( y'=y\ln(x)\)

Réponse

\( y=Ce^{−x}x^x\)

30) La plupart des médicaments présents dans le sang se désintègrent selon l'équation\( y'=cy\), où\( y\) est la concentration du médicament dans le sang. Si la demi-vie d'un médicament est de\( 2\) quelques heures, quelle fraction de la dose initiale reste après les\( 6\) heures de travail ?

31) Un médicament est administré par voie intraveineuse à un patient à raison de\( r\) mg/h et est éliminé de l'organisme à un rythme proportionnel à la quantité de médicament encore présente dans le corps.\( d\) Définissez et résolvez l'équation différentielle, en supposant qu'aucun médicament n'est initialement présent dans le corps.

Réponse: \( y=\frac{r}{d}(1−e^{−dt})\)

32) [T] À quelle fréquence faut-il prendre un médicament si sa dose est de\( 3\) mg, s'il est éliminé à raison de\( c=0.1\) mg/h et si les\( 1\) mg doivent être présents dans le sang en tout temps ?

33) Un réservoir contient un\( 1\) kilogramme de sel dissous dans des\( 100\) litres d'eau. Une solution saline de\( 0.1\) kg de sel/L est pompée dans le réservoir à un débit de\( 2\) L/min et est drainée au même débit. Résolvez la concentration de sel à un moment donné\( t\). Supposons que le réservoir soit bien mélangé.

Réponse: \( y(t)=10−9e^{−t/50}\)

34) Deux solutions salines sont pompées dans un réservoir contenant des\( 10\) kilogrammes de sel dissous dans des\( 1000\) litres d'eau. La première solution de\( 0.2\) kg de sel/L est pompée à un débit de\( 20\) L/min et la seconde solution de\( 0.05\) kg de sel/L est pompée à un débit de\( 5\) L/min. Le réservoir se vide à\( 25\) L/min. Supposons que le réservoir soit bien mélangé. Résolvez la concentration de sel à un moment donné\( t\).

35) [T] Pour le problème précédent, déterminez la quantité de sel contenue dans le réservoir\( 1\) une heure après le début du processus.

Réponse: \( 134.3\)kilogrammes

36) La loi de Torricelli stipule que pour un réservoir d'eau avec un trou dans le fond ayant une section transversale\( A\) et une hauteur d'eau\( h\) au-dessus du fond du réservoir, le taux de variation du volume d'eau s'écoulant du réservoir est proportionnel à la racine carrée de la hauteur de l'eau, selon à\( \dfrac{dV}{dt}=−A\sqrt{2gh}\), où se\( g\) situe l'accélération due à la gravité. Notez que\( \dfrac{dV}{dt}=A\dfrac{dh}{dt}\). Résolvez le problème de valeur initiale qui en résulte pour la hauteur de l'eau, en supposant un réservoir avec un trou d'un rayon de\( 2\) pieds. La hauteur initiale de l'eau est de\( 100\) pieds.

37) Pour le problème précédent, déterminez le temps qu'il faut au réservoir pour se vider.

Réponse: \( 720\)secondes

Pour les problèmes 38 à 44, utilisez la loi de refroidissement de Newton.

38) La base liquide d'une crème glacée a une température initiale de\( 200°F\) avant d'être placée dans un congélateur à température constante de\( 0°F\). Au bout d'\( 1\)une heure, la température de la base de glace est descendue à\( 140°F\). Formulez et résolvez le problème de la valeur initiale pour déterminer la température de la crème glacée.

39) [T] La base liquide d'une crème glacée a une température initiale de\( 210°F\) avant d'être placée dans un congélateur à température constante de\( 20°F\). Après\( 2\) quelques heures, la température de la base de glace est descendue à\( 170°F\). À quelle heure la glace sera-t-elle prête à être consommée ? (Supposons que\( 30°F\) c'est la température optimale pour manger.)

Réponse: \( 24\)heures\( 55\) minutes

40) [T] Vous organisez une soirée de crème glacée. La température extérieure est\( 80°F\) et la glace est à\( 10°F\). Après\( 10\) quelques minutes, la température de la glace a augmenté\( 10°F\). Combien de temps pouvez-vous attendre avant que la glace ne fonde\( 40°F\) ?

41) Vous prenez une tasse de café à température\( 70°C\) et la température ambiante dans la pièce est de\( 20°C\). En supposant une vitesse\( k\) de refroidissement,\( 0.125,\) écrivez et résolvez l'équation différentielle pour décrire la température du café en fonction du temps.

Réponse: \( T(t)=20+50e^{−0.125t}\)

42) [T] Vous prenez une tasse de café à la température\( 70°C\) que vous mettez à l'extérieur, où se situe la température ambiante.\( 0°C.\) Après\( 5\) quelques minutes, dans quelle mesure le café fait-il plus froid ?

43) Vous prenez une tasse de café à température\( 70°C\) et vous versez immédiatement une\( 1\) partie du lait sur des\( 5\) parties de café. Le lait est initialement à température\( 1°C.\) Écrivez et résolvez l'équation différentielle qui régit la température de ce café.

Réponse: \( T(t)=20+38.5e^{−0.125t}\)

44) Vous prenez une tasse de café à température\( 70°C,\) que vous laissez refroidir\( 10\) quelques minutes avant de verser la même quantité de lait\( 1°C\) que dans le problème précédent. Comment la température se compare-t-elle à la tasse précédente après\( 10\) quelques minutes ?

45) Résoudre le problème générique\( y'=ay+b\) avec la condition initiale\( y(0)=c.\)

Réponse: \( y=(c+ba)e^{ax}−\frac{b}{a}\)

46) Prouvez l'équation de base des intérêts composés continus. En supposant un dépôt initial\( P_0\) et un taux d'intérêt de\( r\), configurez et résolvez une équation pour les intérêts composés continuellement.

47) Supposons une quantité initiale de nutriments en\( I\) kilogrammes dans un réservoir de\( L\) litres. Supposons qu'une concentration de\( c\) kg/L soit pompée à un débit de\( r\) L/min. Le réservoir est bien mélangé et vidangé à un débit de\( r\) L/min. Trouvez l'équation décrivant la quantité de nutriments dans le réservoir.

Réponse: \( y(t)=cL+(I−cL)e^{−rt/L}\)

48) Les feuilles s'accumulent sur le tapis forestier à raison de\( 2\) g/cm ² /an et se décomposent également à un rythme\( 90%\) annuel. Écrivez une équation différentielle régissant le nombre de grammes de litière de feuilles par centimètre carré de couverture forestière, en supposant qu'il n'\( 0\)y ait pas de litière de feuilles sur le sol à un moment donné. Ce montant se rapproche-t-il d'une valeur stable ? Quelle est cette valeur ?

49) Les feuilles s'accumulent sur le tapis forestier à raison de\( 4\) g/cm ² /an. Ces feuilles se décomposent à un rythme\( 10%\) annuel. Écrivez une équation différentielle régissant le nombre de grammes de litière de feuilles par centimètre carré de couverture forestière. Ce montant se rapproche-t-il d'une valeur stable ? Quelle est cette valeur ?

Réponse: Équation différentielle :\(\dfrac{dy}{dt} = 4 - 0.1y\)
Solution, le modèle pour cette situation :\( y=40(1−e^{−0.1t})\),
La quantité se rapproche d'une valeur constante de 40 g/cm ²