8.1 : Principes de base des équations différentielles

Last updated
Save as PDF

Page ID: 197412

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Identifiez l'ordre d'une équation différentielle.
Expliquez ce que signifie une solution à une équation différentielle.
Distinguer la solution générale d'une solution particulière d'une équation différentielle.
Identifiez un problème de valeur initiale.
Déterminez si une fonction donnée est une solution à une équation différentielle ou à un problème de valeur initiale.

Le calcul est la mathématique du changement, et les taux de variation sont exprimés par des dérivées. Ainsi, l'une des méthodes les plus courantes d'utilisation du calcul consiste à établir une équation contenant une fonction inconnue\(y=f(x)\) et sa dérivée, connue sous le nom d'équation différentielle. La résolution de telles équations fournit souvent des informations sur la façon dont les quantités changent et permet fréquemment de comprendre comment et pourquoi les changements se produisent.

Les techniques de résolution d'équations différentielles peuvent prendre de nombreuses formes différentes, y compris la solution directe, l'utilisation de graphes ou de calculs informatiques. Nous présentons les principales idées de ce chapitre et les décrivons plus en détail plus loin dans le cours. Dans cette section, nous étudions ce que sont les équations différentielles, comment vérifier leurs solutions, certaines méthodes utilisées pour les résoudre et quelques exemples d'équations courantes et utiles.

équations différentielles générales

Prenons l'équation\(y′=3x^2,\) qui est un exemple d'équation différentielle car elle inclut une dérivée. Il existe une relation entre les variables\(x\) et\(y:y\) est une fonction inconnue de\(x\). De plus, le côté gauche de l'équation est la dérivée de\(y\). Nous pouvons donc interpréter cette équation comme suit : Commencez par une fonction\(y=f(x)\) et prenez sa dérivée. La réponse doit être égale à\(3x^2\). À quelle fonction a une dérivée égale\(3x^2\) ? L'une de ces fonctions l'est\(y=x^3\), donc cette fonction est considérée comme une solution à une équation différentielle.

Définition : équation différentielle

Une équation différentielle est une équation impliquant une fonction inconnue\(y=f(x)\) et une ou plusieurs de ses dérivées. Une solution à une équation différentielle est une fonction\(y=f(x)\) qui satisfait l'équation différentielle lorsque\(f\) et ses dérivées sont substituées dans l'équation.

Consultez ce site Web pour en savoir plus sur ce sujet.

Quelques exemples d'équations différentielles et de leurs solutions figurent dans le tableau\(\PageIndex{1}\).

Tableau\(\PageIndex{1}\) : Exemples d'équations différentielles et leurs solutions
ÉQUATION	Solution
\(y'=2x\)	\(y=x^2\)
\(y'+3y=6x+11\)	\(y=e^{−3x}+2x+3\)
\(y''−3y'+2y=24e^{−2x}\)	\(y=3e^x−4e^{2x}+2e^{−2x}\)

Notez qu'une solution à une équation différentielle n'est pas nécessairement unique, principalement parce que la dérivée d'une constante est zéro. Par exemple,\(y=x^2+4\) est également une solution à la première équation différentielle du tableau\(\PageIndex{1}\). Nous reviendrons sur cette idée un peu plus loin dans cette section. Pour l'instant, concentrons-nous sur ce que signifie pour une fonction le fait d'être la solution à une équation différentielle.

Exemple\(\PageIndex{1}\): Verifying Solutions of Differential Equations

Vérifiez que la fonction\(y=e^{−3x}+2x+3\) est une solution à l'équation différentielle\(y′+3y=6x+11\).

Solution

Pour vérifier la solution, nous calculons d'abord\(y′\) en utilisant la règle de chaîne pour les dérivées. Cela donne\(y′=−3e^{−3x}+2\). Ensuite, nous\(y′\) remplaçons\(y\) et dans la partie gauche de l'équation différentielle :

\((−3e^{−2x}+2)+3(e^{−2x}+2x+3).\)

L'expression résultante peut être simplifiée en distribuant d'abord pour éliminer les parenthèses, en donnant

\(−3e^{−2x}+2+3e^{−2x}+6x+9.\)

La combinaison de termes similaires conduit à l'expression\(6x+11\), qui est égale au côté droit de l'équation différentielle. Ce résultat confirme qu'il s'\(y=e^{−3x}+2x+3\)agit d'une solution de l'équation différentielle.

Exercice\(\PageIndex{1}\)

Vérifiez qu'il\(y=2e^{3x}−2x−2\) s'agit d'une solution à l'équation différentielle\(y′−3y=6x+4.\)

Allusion: Commencez par calculer\(y′\), puis remplacez les deux\(y′\) et\(y\) dans le côté gauche.

Il est pratique de définir les caractéristiques des équations différentielles qui permettent d'en parler plus facilement et de les catégoriser. La caractéristique la plus fondamentale d'une équation différentielle est son ordre.

Définition : ordre d'une équation différentielle

L'ordre d'une équation différentielle est l'ordre le plus élevé de toute dérivée de la fonction inconnue qui apparaît dans l'équation.

Exemple\(\PageIndex{2}\): Identifying the Order of a Differential Equation

La dérivée la plus élevée de l'équation est\(y′\),

Quel est l'ordre de chacune des équations différentielles suivantes ?

\(y′−4y=x^2−3x+4\)
\(x^2y'''−3xy''+xy′−3y=\sin x\)
\(\frac{4}{x}y^{(4)}−\frac{6}{x^2}y''+\frac{12}{x^4}y=x^3−3x^2+4x−12\)

Solution

La dérivée la plus élevée de l'équation est\(y′\) donc l'ordre\(1\).
La dérivée la plus élevée de l'équation est\(y'''\) donc l'ordre\(3\).
La dérivée la plus élevée de l'équation est\(y^{(4)}\) donc l'ordre\(4\).

Exercice\(\PageIndex{2}\)

Quel est l'ordre de l'équation différentielle suivante ?

\((x^4−3x)y^{(5)}−(3x^2+1)y′+3y=\sin x\cos x\)

Allusion: Quelle est la dérivée la plus élevée de l'équation ?

Réponse: \(5\)

Solutions générales et particulières

Nous avons déjà noté que l'équation différentielle\(y′=2x\) comporte au moins deux solutions :\(y=x^2\) et\(y=x^2+4\). La seule différence entre ces deux solutions est le dernier terme, qui est une constante. Et si le dernier terme était une constante différente ? Cette expression sera-t-elle toujours une solution à l'équation différentielle ? En fait, toute fonction de la forme\(y=x^2+C\), où\(C\) représente une constante, est également une solution. La raison en est que la dérivée de\(x^2+C\) est\(2x\), quelle que soit la valeur de\(C\). On peut montrer que toute solution de cette équation différentielle doit être de la forme\(y=x^2+C\). Il s'agit d'un exemple de solution générale à une équation différentielle. Un graphique de certaines de ces solutions est présenté dans la figure\(\PageIndex{1}\). (Remarque : dans ce graphique, nous avons utilisé des valeurs entières paires pour C comprises entre\(−4\) et\(4\). En fait, il n'y a aucune restriction quant à la valeur de\(C\) ; il peut s'agir d'un entier ou non.)

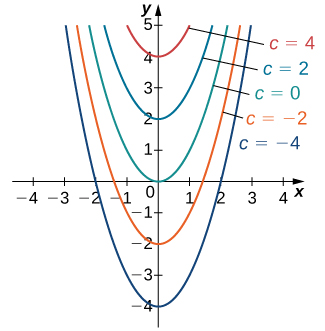
Un graphique d'une famille de solutions à l'équation différentielle y' = 2 x, qui sont de la forme y = x ^ 2 + C. Des paraboles sont dessinées pour les valeurs de C : -4, -2, 0, 2 et 4. — Figure\(\PageIndex{1}\) : Famille de solutions pour l'équation différentielle\(y′=2x.\)

Dans cet exemple, nous sommes libres de choisir la solution de notre choix ; par exemple,\(y=x^2−3\) elle fait partie de la famille des solutions à cette équation différentielle. C'est ce qu'on appelle une solution particulière à l'équation différentielle. Une solution particulière peut souvent être identifiée de manière unique si nous recevons des informations supplémentaires sur le problème.

Exemple\(\PageIndex{3}\): Finding a Particular Solution

Trouvez la solution particulière à l'équation différentielle\(y′=2x\) passant par le point\((2,7)\).

Solution

Toute fonction de la forme\(y=x^2+C\) est une solution à cette équation différentielle. Pour déterminer la valeur de\(C\), nous substituons les valeurs\(x=2\) et\(y=7\) dans cette équation et résolvons pour\(C\) :

\[ \begin{align*} y =x^2+C \\[4pt] 7 =2^2+C \\[4pt] =4+C \\[4pt] C =3. \end{align*}\]

Par conséquent, la solution particulière qui passe par le point\((2,7)\) est\(y=x^2+3\).

Exercice\(\PageIndex{3}\)

Trouvez la solution particulière à l'équation différentielle

\[ y′=4x+3 \nonumber \]

le fait de passer par le point\((1,7),\) donné\(y=2x^2+3x+C\) est une solution générale à l'équation différentielle.

Allusion: Remplacez d'abord\(x=1\) et\(y=7\) insérez dans l'équation, puis résolvez pour\(C\).

Réponse: \[ y=2x^2+3x+2 \nonumber \]

Problèmes liés à la valeur initiale

Habituellement, une équation différentielle donnée comporte un nombre infini de solutions, il est donc naturel de se demander laquelle nous voulons utiliser. Pour choisir une solution, plus d'informations sont nécessaires. Certaines informations spécifiques qui peuvent être utiles sont une valeur initiale, qui est une paire ordonnée utilisée pour trouver une solution particulière.

Une équation différentielle associée à une ou plusieurs valeurs initiales est appelée problème de valeur initiale. La règle générale est que le nombre de valeurs initiales nécessaires à un problème de valeur initiale est égal à l'ordre de l'équation différentielle. Par exemple, si nous avons l'équation différentielle\(y′=2x\), il s'\(y(3)=7\)agit d'une valeur initiale et, lorsqu'elles sont prises ensemble, ces équations forment un problème de valeur initiale. L'équation différentielle\(y''−3y′+2y=4e^x\) est de second ordre, nous avons donc besoin de deux valeurs initiales. En cas de problèmes de valeur initiale d'ordre supérieur à un, la même valeur doit être utilisée pour la variable indépendante. Un exemple de valeurs initiales pour cette équation du second ordre serait\(y(0)=2\) et\(y′(0)=−1.\) Ces deux valeurs initiales ainsi que l'équation différentielle forment un problème de valeur initiale. Ces problèmes sont nommés ainsi parce que la variable indépendante de la fonction inconnue est souvent\(t\), qui représente le temps. Ainsi, une valeur de\(t=0\) représente le début du problème.

Exemple\(\PageIndex{4}\): Verifying a Solution to an Initial-Value Problem

Vérifiez que la fonction\(y=2e^{−2t}+e^t\) est une solution au problème de valeur initiale

\[ y′+2y=3e^t, \quad y(0)=3.\nonumber \]

Solution

Pour qu'une fonction puisse résoudre un problème de valeur initiale, elle doit satisfaire à la fois à l'équation différentielle et à la condition initiale. Pour montrer que cela\(y\) répond à l'équation différentielle, nous commençons par calculer\(y′\). Cela donne\(y′=−4e^{−2t}+e^t\). Ensuite, nous substituons les deux\(y\) et\(y′\) dans la partie gauche de l'équation différentielle et simplifions :

\[ \begin{align*} y′+2y &=(−4e^{−2t}+e^t)+2(2e^{−2t}+e^t) \\[4pt] &=−4e^{−2t}+e^t+4e^{−2t}+2e^t =3e^t. \end{align*}\]

Ceci est égal au côté droit de l'équation différentielle, donc\(y=2e^{−2t}+e^t\) résout l'équation différentielle. Ensuite, nous calculons\(y(0)\) :

\[ y(0)=2e^{−2(0)}+e^0=2+1=3. \nonumber \]

Ce résultat permet de vérifier la valeur initiale. La fonction donnée répond donc au problème de valeur initiale.

Exercice\(\PageIndex{4}\)

Vérifiez qu'il\(y=3e^{2t}+4\sin t\) s'agit d'une solution au problème de valeur initiale

\[ y′−2y=4\cos t−8\sin t,y(0)=3. \nonumber \]

Allusion: Vérifiez d'abord que cela\(y\) résout l'équation différentielle. Vérifiez ensuite la valeur initiale.

Dans l'exemple\(\PageIndex{4}\), le problème de la valeur initiale se composait de deux parties. La première partie était l'équation\(y′+2y=3e^x\) différentielle et la seconde partie était la valeur initiale.\(y(0)=3.\) Ces deux équations ensemble formaient le problème de la valeur initiale.

Il en va de même en général. Un problème de valeur initiale comportera deux parties : l'équation différentielle et la condition initiale. L'équation différentielle comporte une famille de solutions, et la condition initiale détermine la valeur de\(C\). La famille de solutions à l'équation différentielle dans l'exemple\(\PageIndex{4}\) est donnée par\(y=2e^{−2t}+Ce^t.\) Cette famille de solutions est illustrée sur la figure\(\PageIndex{2}\), avec la solution particulière\(y=2e^{−2t}+e^t\) étiquetée.

Un graphique d'une famille de solutions à l'équation différentielle y' + 2 y = 3 e ^ t, qui sont de la forme y = 2 e ^ (-2 t) + C e ^ t. Les versions avec C = 1, 0,5 et -0,2 sont présentées, parmi d'autres non étiquetées. Pour toutes les valeurs de C, la fonction augmente rapidement pour t < 0 lorsque t passe à l'infini négatif. Pour C — Figure\(\PageIndex{2}\) : Famille de solutions à l'équation différentielle\(y′+2y=3e^t\). La solution particulière\(y=2e^{−2t}+e^t\) est étiquetée.

Exemple\(\PageIndex{5}\): Solving an Initial-value Problem

Résolvez le problème de valeur initiale suivant :

\[ y′=3e^x+x^2−4,y(0)=5. \nonumber \]

Solution

La première étape pour résoudre ce problème de valeur initiale consiste à trouver une famille générale de solutions. Pour ce faire, nous trouvons une antidérivée des deux côtés de l'équation différentielle

\[∫y′\,dx=∫(3e^x+x^2−4)\,dx, \nonumber \]

à savoir,

\(y+C_1=3e^x+\frac{1}{3}x^3−4x+C_2\).

Nous sommes en mesure d'intégrer les deux parties parce que le terme y apparaît tout seul. Notez qu'il existe deux constantes d'intégration :\(C_1\) et\(C_2\). Résoudre cette équation pour\(y\) donner

\(y=3e^x+\frac{1}{3}x^3−4x+C_2−C_1.\)

Parce que\(C_1\) et\(C_2\) sont tous deux des constantes,\(C_2−C_1\) c'est aussi une constante. Nous pouvons donc définir\(C=C_2−C_1,\) ce qui conduit à l'équation

\(y=3e^x+\frac{1}{3}x^3−4x+C.\)

Ensuite, nous déterminons la valeur de\(C\). Pour ce faire, nous substituons\(x=0\) et\(y=5\) dans cette équation et résolvons pour\(C\) :

\[ \begin{align*} 5 &=3e^0+\frac{1}{3}0^3−4(0)+C \\[4pt] 5 &=3+C \\[4pt] C&=2 \end{align*}. \nonumber \]

Nous remplaçons maintenant la valeur\(C=2\) dans l'équation générale. La solution au problème de la valeur initiale est\(y=3e^x+\frac{1}{3}x^3−4x+2.\)

Analyse

La différence entre une solution générale et une solution particulière est qu'une solution générale implique une famille de fonctions, définies explicitement ou implicitement, de la variable indépendante. La ou les valeurs initiales déterminent quelle solution particulière de la famille de solutions satisfait aux conditions souhaitées.

Exercice\(\PageIndex{5}\)

Résolvez le problème de la valeur initiale

\[ y′=x^2−4x+3−6e^x,y(0)=8. \nonumber \]

Allusion: Prenez d'abord l'antidérivée des deux côtés de l'équation différentielle. Remplacez ensuite\(x=0\) et\(y=8\) dans l'équation résultante et résolvez pour\(C\).

Réponse: \(y=\frac{1}{3}x^3−2x^2+3x−6e^x+14\)

Dans les applications de physique et d'ingénierie, nous prenons souvent en compte les forces agissant sur un objet et utilisons ces informations pour comprendre le mouvement qui peut en résulter. Par exemple, si nous commençons par un objet à la surface de la Terre, la force principale qui agit sur cet objet est la gravité. Les physiciens et les ingénieurs peuvent utiliser ces informations, ainsi que la deuxième loi du mouvement de Newton (sous forme d'équation\(F=ma\), où\(F\) représente la force,\(m\) la masse et\(a\) l'accélération), pour dériver une équation qui peut être résolue.

Une photo d'une balle de baseball avec une flèche en dessous pointant vers le bas. La flèche est étiquetée g = -9,8 m/sec ^ 2. — Figure\(\PageIndex{3}\) : Pour une balle de baseball qui tombe en l'air, la seule force qui agit sur elle est la gravité (en négligeant la résistance à l'air).

Dans la figure,\(\PageIndex{3}\) nous supposons que la seule force agissant sur une balle de baseball est la force de gravité. Cette hypothèse ignore la résistance de l'air. (La force due à la résistance de l'air sera examinée dans une discussion ultérieure.) L'accélération due à la gravité à la surface de la Terre, g, est d'environ\(9.8\,\text{m/s}^2\). Nous introduisons un cadre de référence, où la surface de la Terre se trouve à une hauteur de 0 mètre. \(v(t)\)Représentent la vitesse de l'objet en mètres par seconde. Si\(v(t)>0\), la balle monte, et si\(v(t)<0\), la balle tombe (Figure).

Une photo d'une balle de baseball avec une flèche au-dessus pointant vers le haut et une flèche en dessous pointant vers le bas. La flèche pointant vers le haut est étiquetée v (t) — Figure\(\PageIndex{4}\) : Vitesses possibles pour une balle montante ou descendante.

Notre objectif est de résoudre la vélocité\(v(t)\) à tout moment\(t\). Pour ce faire, nous avons mis en place un problème de valeur initiale. Supposons que la masse de la balle soit\(m\), où elle\(m\) est mesurée en kilogrammes. Nous utilisons la deuxième loi de Newton, selon laquelle la force agissant sur un objet est égale à sa masse multipliée par son accélération\((F=ma)\). L'accélération est la dérivée de la vitesse, donc\(a(t)=v′(t)\). Par conséquent, la force agissant sur la balle de baseball est donnée par\(F=mv′(t)\). Cependant, cette force doit être égale à la force de gravité agissant sur l'objet, qui (toujours en utilisant la deuxième loi de Newton) est donnée par\(F_g=−mg\), puisque cette force agit vers le bas. Nous obtenons donc l'équation\(F=F_g\), qui devient\(mv′(t)=−mg\). En divisant les deux côtés de l'équation par, on\(m\) obtient l'équation

\[ v′(t)=−g. \nonumber \]

Notez que cette équation différentielle reste la même quelle que soit la masse de l'objet.

Nous avons maintenant besoin d'une valeur initiale. Comme nous résolvons la vitesse, il est logique, dans le contexte du problème, de supposer que nous connaissons la vitesse initiale, ou la vitesse au moment.\(t=0.\) Cela est indiqué par\(v(0)=v_0.\)

Exemple\(\PageIndex{6}\): Velocity of a Moving Baseball

Une balle de baseball est lancée vers le haut d'une hauteur de plusieurs\(3\) mètres au-dessus de la surface de la Terre avec une vitesse initiale de\(10\) m/s, et la seule force qui agit sur elle est la gravité. La balle a une masse de\(0.15\) kg à la surface de la Terre.

Détermine la vélocité\(v(t)\) de la balle de base à un moment donné\(t\).
Quelle est sa vitesse après\(2\) quelques secondes ?

Solution

a. D'après la discussion précédente, l'équation différentielle qui s'applique dans cette situation est

\(v′(t)=−g,\)

où\(g=9.8\, \text{m/s}^2\). La condition initiale est\(v(0)=v_0\), où\(v_0=10\) m/s. Par conséquent, le problème de valeur initiale est\(v′(t)=−9.8\,\text{m/s}^2,\,v(0)=10\) m/s.

La première étape pour résoudre ce problème de valeur initiale consiste à prendre l'antidérivée des deux côtés de l'équation différentielle. Cela donne

\[\int v′(t)\,dt=∫−9.8\,dt \nonumber \]

\(v(t)=−9.8t+C.\)

La prochaine étape consiste à résoudre\(C\). Pour ce faire,\(t=0\) remplacez par\(v(0)=10\) :

\[ \begin{align*} v(t) &=−9.8t+C \\[4pt] v(0) &=−9.8(0)+C \\[4pt] 10 &=C. \end{align*}\]

Par conséquent\(C=10\), et la fonction de vitesse est donnée par\(v(t)=−9.8t+10.\)

b. Pour trouver la vélocité après\(2\) quelques secondes, remplacez\(t=2\) par\(v(t)\).

\[ \begin{align*} v(t)&=−9.8t+10 \\[4pt] v(2)&=−9.8(2)+10 \\[4pt] v(2) &=−9.6\end{align*}\]

Les unités de vitesse sont les mètres par seconde. La réponse étant négative, l'objet tombe à une vitesse de\(9.6\) m/s.

Exercice\(\PageIndex{6}\)

Supposons qu'un rocher tombe du repos d'une hauteur de plusieurs\(100\) mètres et que la seule force agissant sur elle est la gravité. Trouvez une équation pour la vitesse\(v(t)\) en fonction du temps, mesurée en mètres par seconde.

Allusion: Quelle est la vitesse initiale de la roche ? Utilisez-la avec l'équation différentielle de l'exemple\(\PageIndex{6}\) pour créer un problème de valeur initiale, puis résolvez-le pour\(v(t)\).

Réponse: \(v(t)=−9.8t\)

Une question naturelle à se poser après avoir résolu ce type de problème est de savoir à quelle hauteur l'objet se trouvera au-dessus de la surface de la Terre à un moment donné. \(s(t)\)Dénotons la hauteur de l'objet au-dessus de la surface de la Terre, mesurée en mètres. Comme la vitesse est la dérivée de la position (dans ce cas, la hauteur), cette hypothèse donne l'équation\(s′(t)=v(t)\). Une valeur initiale est nécessaire ; dans ce cas, la hauteur initiale de l'objet fonctionne bien. Supposons que la hauteur initiale soit donnée par l'équation\(s(0)=s_0\). Ensemble, ces hypothèses posent le problème de la valeur initiale

\[ s′(t)=v(t),s(0)=s_0. \nonumber \]

Si la fonction de vitesse est connue, il est possible de résoudre également la fonction de position.

Exemple\(\PageIndex{7}\): Height of a Moving Baseball

Une balle de baseball est lancée vers le haut à une hauteur de\(3\) mètres au-dessus de la surface de la Terre avec une vitesse initiale de\(10m/s\), et la seule force qui agit sur elle est la gravité. La balle a une masse de\(0.15\) kilogramme à la surface de la Terre.

Trouvez la position\(s(t)\) de la balle de baseball à un moment donné\(t\).
Quelle est sa hauteur au bout de\(2\) quelques secondes ?

Solution

Nous savons déjà que la fonction de vitesse de ce problème est\(v(t)=−9.8t+10\). La hauteur initiale de la balle de baseball est de\(3\) mètres, donc\(s_0=3\). Par conséquent, le problème de la valeur initiale pour cet exemple est

Pour résoudre le problème de la valeur initiale, on trouve d'abord les antidérivés :

\[∫s′(t)\,dt=∫(−9.8t+10)\,dt \nonumber \]

\(s(t)=−4.9t^2+10t+C.\)

Ensuite, nous\(t=0\) remplaçons et résolvons\(C\) :

\(s(t)=−4.9t^2+10t+C\)

\(s(0)=−4.9(0)^2+10(0)+C\)

\(3=C\).

Par conséquent, la fonction de position est\(s(t)=−4.9t^2+10t+3.\)

b. La hauteur de la balle après la\(2\) seconde est donnée par\(s(2):\)

\(s(2)=−4.9(2)^2+10(2)+3=−4.9(4)+23=3.4.\)

La balle se trouve donc\(3.4\) à quelques mètres au-dessus de la surface de la Terre après\(2\) quelques secondes. Il convient de noter que la masse de la balle s'est complètement annulée au cours du processus de résolution du problème.

Concepts clés

Une équation différentielle est une équation impliquant une fonction\(y=f(x)\) et une ou plusieurs de ses dérivées. Une solution est une fonction\(y=f(x)\) qui satisfait l'équation différentielle lorsque\(f\) et ses dérivées sont substituées dans l'équation.
L'ordre d'une équation différentielle est l'ordre le plus élevé de toute dérivée de la fonction inconnue qui apparaît dans l'équation.
Une équation différentielle associée à une valeur initiale est appelée problème de valeur initiale. Pour résoudre un problème de valeur initiale, trouvez d'abord la solution générale à l'équation différentielle, puis déterminez la valeur de la constante. Les problèmes liés à la valeur initiale ont de nombreuses applications en science et en ingénierie.

Lexique

équation différentielle: une équation impliquant une fonction\(y=y(x)\) et une ou plusieurs de ses dérivées

solution générale (ou famille de solutions): l'ensemble des solutions à une équation différentielle donnée

valeur (s) initiale (s): une valeur ou un ensemble de valeurs auxquelles une solution d'une équation différentielle satisfait pour une valeur fixe de la variable indépendante

vitesse initiale: la vitesse au moment\(t=0\)

problème de valeur initiale: une équation différentielle associée à une ou plusieurs valeurs initiales

ordre d'une équation différentielle: l'ordre le plus élevé de toute dérivée de la fonction inconnue qui apparaît dans l'équation

solution particulière: membre d'une famille de solutions à une équation différentielle qui satisfait une condition initiale particulière

solution à une équation différentielle: une fonction\(y=f(x)\) qui satisfait une équation différentielle donnée