5.2 : L'intégrale définie

Objectifs d'apprentissage

• Précisez la définition de l'intégrale définie.
• Expliquez les termes integrand, limites d'intégration et variable d'intégration.
• Expliquez quand une fonction est intégrable.
• Décrivez la relation entre la surface intégrale définie et la surface nette.
• Utilisez la géométrie et les propriétés d'intégrales définies pour les évaluer.
• Calculez la valeur moyenne d'une fonction.

Dans la section précédente, nous avons défini l'aire sous une courbe en termes de sommes de Riemann :

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]

Cependant, cette définition était assortie de restrictions. Nous\(f(x)\) devions être continus et non négatifs. Malheureusement, les problèmes du monde réel ne répondent pas toujours à ces restrictions. Dans cette section, nous verrons comment appliquer le concept de l'aire sous la courbe à un ensemble plus large de fonctions en utilisant l'intégrale définie.

Définition et notation

L'intégrale définie généralise le concept de l'aire sous une courbe. Nous levons les exigences qui\(f(x)\) sont continues et non négatives et définissons l'intégrale définie comme suit.

Définition : Intégrale définie

Si\(f(x)\) est une fonction définie sur un intervalle,\([a,b],\) l'intégrale définie\(f\) de\(a\) à\(b\) est donnée par

\[∫^b_af(x)\,dx=\lim_{n→∞} \sum_{i=1}^nf(x^∗_i)Δx, \nonumber \]

à condition que la limite existe. Si cette limite existe, la fonction\(f(x)\) est dite intégrable sur\([a,b]\), ou est une fonction intégrable.

Le symbole intégral de la définition précédente doit vous sembler familier. Nous avons vu une notation similaire dans le chapitre sur les applications des dérivés, où nous avons utilisé le symbole intégral indéfini (sans le\(a\) et le\(b\) dessus et le dessous) pour représenter un antidérivé. Bien que la notation des intégrales indéfinies puisse ressembler à celle d'une intégrale définie, elles ne sont pas identiques. Une intégrale définie est un nombre. Une intégrale indéfinie est une famille de fonctions. Plus loin dans ce chapitre, nous examinerons comment ces concepts sont liés. Cependant, une attention particulière doit toujours être portée à la notation afin de savoir si nous travaillons avec une intégrale définie ou une intégrale indéfinie.

La notation intégrale remonte à la fin du XVIIe siècle et constitue l'une des contributions de Gottfried Wilhelm Leibniz, souvent considéré comme le codécouvreur du calcul, avec Isaac Newton. Le symbole d'intégration\(∫\) est allongé\(S\), suggérant un sigma ou une sommation. Sur une intégrale définie, au-dessus et en dessous du symbole de sommation se trouvent les limites de l'intervalle.\([a,b].\) Les nombres\(a\) et\(b\) sont des\(x\) valeurs et sont appelés limites d'intégration ; plus précisément,\(a\) il s'agit de la limite inférieure et\(b\) de la limite supérieure. Pour clarifier, nous utilisons la limite de mots de deux manières différentes dans le contexte de l'intégrale définie. Tout d'abord, nous parlons de la limite d'une somme, car\(n→∞.\) ensuite, les limites de la région sont appelées limites de l'intégration.

Nous appelons\(f(x)\) la fonction integrand, et l'\(dx\)indique qu'il\(f(x)\) s'agit d'une fonction par rapport à\(x\), appelée variable d'intégration. Notez que, comme l'indice dans une somme, la variable d'intégration est une variable fictive et n'a aucun impact sur le calcul de l'intégrale. Nous pouvons utiliser n'importe quelle variable comme variable d'intégration :

\[∫^b_af(x)\,dx=∫^b_af(t)\,dt=∫^b_af(u)\,du \nonumber \]

Nous avons déjà discuté du fait que si elle\(f(x)\) est continue\([a,b],\), la limite\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) existe et est unique. Cela conduit au théorème suivant, que nous énonçons sans preuve.

Les fonctions continues sont intégrables

Si\(f(x)\) est activé en continu\([a,b]\), alors\(f\) est intégrable sur\([a,b].\)

Les fonctions qui ne sont pas continues\([a,b]\) peuvent tout de même être intégrables, en fonction de la nature des discontinuités. Par exemple, les fonctions comportant un nombre fini de discontinuités de saut ou de discontinuités amovibles sur un intervalle fermé peuvent être intégrées.

Il convient également de noter ici que nous avons conservé l'utilisation d'une partition régulière dans les sommes de Riemann. Cette restriction n'est pas strictement nécessaire. N'importe quelle partition peut être utilisée pour former une somme de Riemann. Toutefois, si une partition non régulière est utilisée pour définir l'intégrale définie, il ne suffit pas de prendre la limite car le nombre de sous-intervalles passe à l'infini. Au lieu de cela, nous devons prendre la limite lorsque la largeur du plus grand sous-intervalle passe à zéro. Cela introduit une notation un peu plus complexe dans nos limites et complique les calculs sans vraiment acquérir de connaissances supplémentaires. Nous nous en tenons donc à des partitions régulières pour les sommes de Riemann.

Exemple\(\PageIndex{1}\): Evaluating an Integral Using the Definition

Utilisez la définition de l'intégrale définie pour évaluer\(\displaystyle ∫^2_0x^2\,dx.\) Utilisez une approximation de l'extrémité droite pour générer la somme de Riemann.

Solution

Nous voulons d'abord établir une somme Riemann. Sur la base des limites de l'intégration, nous avons\(a=0\) et\(b=2\). Pour\(i=0,1,2,…,n\),\(P={x_i}\) soyons une partition normale de\([0,2].\) Then

\[Δx=\dfrac{b−a}{n}=\dfrac{2}{n}. \nonumber \]

Puisque nous utilisons une approximation de l'extrémité droite pour générer des sommes de Riemann, pour chacune d'elles\(i\), nous devons calculer la valeur de la fonction à l'extrémité droite de l'intervalle.\([x_{i−1},x_i].\) L'extrémité droite de l'intervalle est\(x_i\), et puisque\(P\) c'est une partition régulière,

\[x_i=x_0+iΔx=0+i\left[\dfrac{2}{n}\right]=\dfrac{2i}{n}.\nonumber \]

Ainsi, la valeur de la fonction à l'extrémité droite de l'intervalle est

\[f(x_i)=x^2_i=\left(\dfrac{2i}{n}\right)^2=\dfrac{4i^2}{n^2}.\nonumber \]

Ensuite, la somme de Riemann prend la forme

\[\sum_{i=1}^nf(x_i)Δx=\sum_{i=1}^n\left(\dfrac{4i^2}{n^2}\right)\dfrac{2}{n}=\sum_{i=1}^n\dfrac{8i^2}{n^3}=\dfrac{8}{n^3}\sum_{i=1}^ni^2.\nonumber \]

En utilisant la formule de sommation pour\(\displaystyle \sum_{i=1}^ni^2\), nous avons

\[\begin{align*} \sum_{i=1}^nf(x_i)Δx &=\dfrac{8}{n^3}\sum_{i=1}^ni^2 \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{n(n+1)(2n+1)}{6}\right] \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{2n^3+3n^2+n}{6}\right] \\[4pt] &=\dfrac{16n^3+24n^2+n}{6n^3} \\[4pt] &=\dfrac{8}{3}+\dfrac{4}{n}+\dfrac{1}{6n^2}. \end{align*}\]

Maintenant, pour calculer l'intégrale définie, nous devons prendre la limite comme\(n→∞\). Nous obtenons

\ [\ begin {align*} ^2_0x^2dx &= \ lim_ {n→∞} \ sum_ {i=1} ^nf (x_i) Δx \ \ [4 points]
&= \ lim_ {n→∞} \ left (\ dfrac {8} {3} + \ dfrac {4} {n} + \ dfrac {1} {6} n^2} \ droite) \ \ [4 points]
&= \ lim_ {n→∞} \ gauche (\ dfrac {8} {3} \ droite) + \ lim_ {n→∞} \ gauche (\ dfrac {4} {n} \ droite) + \ lim_ {n→∞} \ gauche (\ dfrac {1} {6n^2} \ droite) \ [[4 points]
&= \ dfrac {8} {3} +0+0= \ dfrac {8} {3}. \ end {align*} \]

Exercice\(\PageIndex{1}\)

Utilisez la définition de l'intégrale définie pour évaluer\(\displaystyle ∫^3_0(2x−1)\,dx\).

Utilisez une approximation de l'extrémité droite pour générer la somme de Riemann.

Allusion

Utilisez la stratégie de résolution décrite dans Example\(\PageIndex{1}\).

Réponse

6

Évaluation des intégrales définies

Évaluer des intégrales définies de cette manière peut s'avérer assez fastidieux en raison de la complexité des calculs. Plus loin dans ce chapitre, nous développons des techniques pour évaluer des intégrales définies sans prendre de limites aux sommes de Riemann. Cependant, pour l'instant, nous pouvons nous fier au fait que les intégrales définies représentent l'aire sous la courbe, et nous pouvons évaluer des intégrales définies en utilisant des formules géométriques pour calculer cette surface. Nous faisons cela pour confirmer que les intégrales définies représentent effectivement des aires, afin que nous puissions ensuite discuter de la marche à suivre dans le cas d'une courbe d'une fonction tombant en dessous de l'\(x\)axe.

Exemple\(\PageIndex{2}\): Using Geometric Formulas to Calculate Definite Integrals

Utilisez la formule de l'aire d'un cercle pour évaluer\(\displaystyle ∫^6_3\sqrt{9−(x−3)^2}\,dx\).

Solution

La fonction décrit un demi-cercle de rayon 3. Pour trouver

\[∫^6_3\sqrt{9−(x−3)^2}\,dx \nonumber \]

nous voulons trouver l'aire sous la courbe sur l'intervalle.\([3,6].\) La formule pour l'aire d'un cercle est\(A=πr^2\). L'aire d'un demi-cercle ne représente que la moitié de l'aire d'un cercle, ou\(A=\dfrac{1}{2}πr^2\). La zone ombrée de la figure\(\PageIndex{1}\) couvre la moitié du demi-cercle, ou\(A=\dfrac{1}{4}πr^2\). Ainsi,

\[∫^6_3\sqrt{9−(x−3)^2}\,dx=\dfrac{1}{4}π(3)^2=\dfrac{9}{4}π≈7.069. \nonumber \]

Figure\(\PageIndex{1}\) : La valeur de l'intégrale de la fonction\(f(x)\) sur l'intervalle\([3,6]\) est l'aire de la région ombrée.

Exercice\(\PageIndex{2}\)

Utilisez la formule de l'aire d'un trapèze pour évaluer\(\displaystyle ∫^4_2(2x+3)\,dx\).

Allusion

Tracez la fonction\(f(x)\) et calculez la surface sous la fonction sur l'intervalle\([2,4].\)

Réponse

18 unités carrées

Aire et intégrale définie

Lorsque nous avons défini l'intégrale définie, nous avons levé l'exigence selon laquelle elle devait\(f(x)\) être non négative. Mais comment interpréter « l'aire sous la courbe » lorsqu'elle\(f(x)\) est négative ?

Zone nette signée

Revenons à la somme de Riemann. Considérez, par exemple, la fonction\(f(x)=2−2x^2\) (illustrée sur la figure\(\PageIndex{2}\)) sur l'intervalle\([0,2]\). Utilisez\(n=8\) et choisissez {\(x^∗_i\)} comme extrémité gauche de chaque intervalle. Construisez un rectangle sur chaque sous-intervalle de hauteur\(f(x^∗_i)\) et de largeur\(Δx\). Lorsque la valeur\(f(x^∗_i)\) est positive, le produit\(f(x^∗_i)Δx\) représente l'aire du rectangle, comme précédemment. Toutefois, lorsque la valeur\(f(x^∗_i)\) est négative, le produit\(f(x^∗_i)Δx\) représente le négatif de l'aire du rectangle. La somme de Riemann devient alors

\[\sum_{i=1}^8f(x^∗_i)Δx= (\text{Area of rectangles above the }x\text{-axis})−(\text{Area of rectangles below the }x\text{-axis}) \nonumber \]

Figure\(\PageIndex{2}\) : Pour une fonction partiellement négative, la somme de Riemann est la surface des rectangles au-dessus de l'\(x\)axe -moins la surface des rectangles situés en dessous de l'\(x\)axe.

En prenant la limite lorsque\(n→∞,\) la somme de Riemann s'approche de l'aire située entre la courbe au-dessus de\(x\) l'axe\(x\) -et l'axe -, moins l'aire entre la courbe située sous l'\(x\)axe -et l'\(x\)axe -, comme indiqué sur la figure\(\PageIndex{3}\). Ensuite,

\[\int^2_0f(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=A_1−A_2. \nonumber \]

La quantité\(A_1−A_2\) est appelée surface nette signée.

Figure\(\PageIndex{3}\) : Dans la limite, l'intégrale définie est égale à la surface\(A_1\) moins la surface\(A_2\), ou à la surface nette signée.

Notez que la surface nette signée peut être positive, négative ou nulle. Si la zone au-dessus de l'\(x\)axe est plus grande, la surface nette signée est positive. Si la zone située sous l'\(x\)axe -est plus grande, la surface nette signée est négative. Si les zones situées au-dessus et en dessous de\(x\) l'axe sont égales, la surface nette signée est nulle.

Exemple\(\PageIndex{3}\): Finding the Net Signed Area

Trouvez la zone nette signée entre la courbe de la fonction\(f(x)=2x\) et l'\(x\)axe -sur l'intervalle\([−3,3].\)

Solution

La fonction produit une ligne droite qui forme deux triangles : l'un allant de\(x=−3\) à\(x=0\) et l'autre de\(x=0\) à\(x=3\) (Figure\(\PageIndex{4}\)). En utilisant la formule géométrique pour l'aire d'un triangle\(A=\dfrac{1}{2}bh\), l'aire du triangle\(A_1\), au-dessus de l'axe, est

\(A_1=\dfrac{1}{2}3(6)=9\),

où\(3\) est la base et\(2(3)=6\) la hauteur. L'aire du triangle\(A_2\), en dessous de l'axe, est

\(A_2=\dfrac{1}{2}(3)(6)=9,\)

où\(3\) est la base et\(6\) la hauteur. Ainsi, la surface nette est

\(\displaystyle ∫^3_{−3}2x\,dx=A_1−A_2=9−9=0.\)

Figure\(\PageIndex{4}\) : L'aire au-dessus de la courbe et sous l'\(x\)axe -est égale à la surface située sous la courbe et au-dessus de\(x\) l'axe.

Analyse

Si\(A_1\) est la zone située au-dessus de l'\(x\)axe -et\(A_2\) la zone située en dessous de\(x\) l'axe -, alors la surface nette est\(A_1−A_2\). Les aires des deux triangles étant égales, la surface nette est nulle.

Exercice\(\PageIndex{3}\)

Trouvez la zone nette signée\(f(x)=x−2\) sur l'intervalle\([0,6]\), illustrée dans l'image suivante.

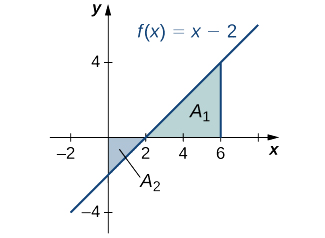
Allusion

Utilisez la méthode de résolution décrite dans l'exemple\(\PageIndex{3}\).

Réponse

6

Surface totale

L'une des applications de l'intégrale définie consiste à déterminer le déplacement lorsqu'on lui donne une fonction de vitesse. Elle\(v(t)\) représente la vitesse d'un objet en fonction du temps, alors la zone située sous la courbe nous indique à quelle distance se trouve l'objet par rapport à sa position initiale. Il s'agit d'une application très importante de l'intégrale définie, et nous l'examinerons plus en détail plus loin dans le chapitre. Pour l'instant, nous allons simplement examiner quelques notions de base pour comprendre comment cela fonctionne en étudiant les vitesses constantes.

Lorsque la vitesse est constante, l'aire sous la courbe est simplement la vitesse multipliée par le temps. Cette idée est déjà très familière. Si une voiture s'éloigne de sa position de départ en ligne droite à une vitesse de\(70\) mi/h pendant des\(2\) heures, elle se trouve à des\(140\) kilomètres de sa position initiale (Figure\(\PageIndex{5}\)). En utilisant la notation intégrale, nous avons

\[∫^2_0 70\,dt=140 \,\text{miles}. \nonumber \]

Figure\(\PageIndex{5}\) : La zone située sous la courbe\(v(t)=70\) indique la distance entre la voiture et son point de départ à un moment donné.

Dans le contexte du déplacement, la zone nette signée nous permet de prendre en compte la direction. Si une voiture roule tout droit vers le nord à une vitesse de 60 mi/h pendant 2 heures, elle se trouve à 120 miles au nord de sa position de départ. Si la voiture fait ensuite demi-tour et roule vers le sud à une vitesse de 40 mi/h pendant 3 heures, elle retrouvera sa position de départ (Figure\(\PageIndex{6}\)). Encore une fois, en utilisant la notation intégrale, nous avons

\[\int^2_060\,dt+∫^5_2−40\,dt=120−120=0.\nonumber \]

Dans ce cas, le déplacement est nul.

Figure\(\PageIndex{6}\) : La surface au-dessus de l'axe et la zone située en dessous de l'axe sont égales, de sorte que la surface nette signée est nulle.

Supposons que nous voulions connaître la distance totale parcourue par la voiture, quelle que soit la direction. Dans ce cas, nous voulons connaître l'aire située entre la courbe et l'\(t\)axe y, que cette zone se trouve au-dessus ou en dessous de l'axe. C'est ce que l'on appelle la superficie totale.

Graphiquement, il est plus facile de penser à calculer la surface totale en additionnant les zones situées au-dessus de l'axe et les zones situées en dessous de l'axe (plutôt que de soustraire les zones situées sous l'axe, comme nous l'avons fait pour la surface nette signée). Pour ce faire mathématiquement, nous utilisons la fonction des valeurs absolues. Ainsi, la distance totale parcourue par la voiture est

\[\int^2_0|60|\,dt+∫^5_2|−40|\,dt=∫^2_060\,dt+∫^5_240\,dt=120+120=240.\nonumber \]

En rassemblant ces idées de manière formelle, nous énonçons les définitions suivantes.

Définition : Zone nette signée

\(f(x)\)Soit une fonction intégrable définie sur un intervalle\([a,b]\). \(A_1\)Représentent la zone située entre\(f(x)\) et l'\(x\)axe -qui se trouve au-dessus de l'axe et\(A_2\) représentons la zone située entre\(f(x)\) et l'\(x\)axe -qui se trouve en dessous de l'axe. Ensuite, la zone nette signée entre\(f(x)\) et l'\(x\)axe -est donnée par

\[∫^b_af(x)\,dx=A_1−A_2. \nonumber \]

La surface totale entre\(f(x)\) et l'\(x\)axe -est donnée par

\[∫^b_a|f(x)|\,dx=A_1+A_2. \nonumber \]

Exemple\(\PageIndex{4}\): Finding the Total Area

Détermine la surface totale entre\(f(x)=x−2\) et l'\(x\)axe -sur l'intervalle\([0,6].\)

Solution

Calculez le\(x\) paramètre -intercept comme\((2,0)\) (définissez\(y=0,\) solve pour\(x\)). Pour trouver la surface totale, prenez la zone située sous l'\(x\)axe -sur le sous-intervalle\([0,2]\) et ajoutez-la à la zone située au-dessus de l'\(x\)axe -sur le sous-intervalle\([2,6]\) (Figure\(\PageIndex{7}\)).

Figure\(\PageIndex{7}\) : La surface totale entre la ligne et l'\(x\)axe Y au-dessus\([0,6]\) est\(A_2\) plus\(A_1\).

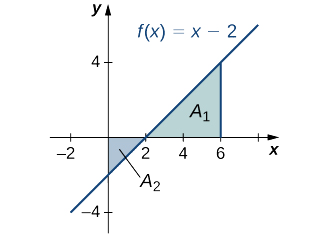
Nous avons

\[∫^6_0|(x−2)|\,dx=A_2+A_1. \nonumber \]

Ensuite, en utilisant la formule pour l'aire d'un triangle, nous obtenons

\[A_2=\dfrac{1}{2}bh=\dfrac{1}{2}⋅2⋅2=2 \nonumber \]

\[A_1=\dfrac{1}{2}bh=\dfrac{1}{2}⋅4⋅4=8. \nonumber \]

La superficie totale est donc

\[A_1+A_2=8+2=10\,\text{units}^2. \nonumber \]

Exercice\(\PageIndex{4}\)

Détermine l'aire totale entre la fonction\(f(x)=2x\) et l'\(x\)axe -sur l'intervalle\([−3,3].\)

Allusion

Passez en revue la stratégie de résolution dans Example\(\PageIndex{4}\).

Réponse

\(18\,\text{units}^2\)

Propriétés de l'intégrale définie

Les propriétés des intégrales indéfinies s'appliquent également aux intégrales définies. Les intégrales définies possèdent également des propriétés liées aux limites de l'intégration. Ces propriétés, ainsi que les règles d'intégration que nous examinerons plus loin dans ce chapitre, nous aident à manipuler des expressions pour évaluer des intégrales définies.

Règle : Propriétés de l'intégrale définie

1. \[ \begin{equation} ∫^a_af(x)\,dx=0 \end{equation} \nonumber \]

Si les limites de l'intégration sont les mêmes, l'intégrale n'est qu'une ligne et ne contient aucune zone.

2. \[∫^a_bf(x)\,dx=−∫^b_af(x)\,dx \nonumber \]

Si les limites sont inversées, placez un signe négatif devant l'intégrale.

3. \[∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx \nonumber \]

L'intégrale d'une somme est la somme des intégrales.

4. \[∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx \nonumber \]

L'intégrale d'une différence est la différence des intégrales.

5. \[∫^b_acf(x)\,dx=c∫^b_af(x)\,dx \nonumber \]

pour constant\(c\). L'intégrale du produit d'une constante et d'une fonction est égale à la constante multipliée par l'intégrale de la fonction.

6. \[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx \nonumber \]

Bien que cette formule s'applique normalement entre\(a\) et\(b\), elle\(c\) est valable pour toutes les valeurs de\(a\), et\(b\)\(c\), à condition qu'elle\(f(x)\) soit intégrable sur l'intervalle le plus grand.

Exemple\(\PageIndex{5}\): Using the Properties of the Definite Integral

Utilisez les propriétés de l'intégrale définie pour exprimer l'intégrale définie de\(f(x)=−3x^3+2x+2\) sur l'intervalle\([−2,1]\) sous la forme de la somme de trois intégrales définies.

Solution

En utilisant la notation intégrale, nous\(\displaystyle ∫^1_{−2}(−3x^3+2x+2)\,dx.\) avons appliqué les propriétés 3. et 5. pour obtenir

\ [\ begin {align*} ^1_ {−2} (−3x^3+2x+2) \, dx =^1_ {−2} −3x^3 \, dx+98.^1_ {−2} 2x \, dx+90^1_ {−2} 2 \, dx \ \ [4 points]
=−3^1_ {−2} x^1_ {−2} x^3 \, dx+2±^1_ {−2} x \, dx+size^1_ {−2} 2 \, dx. \ end {align*} \ nonumber \]

Exercice\(\PageIndex{5}\)

Utilisez les propriétés de l'intégrale définie pour exprimer l'intégrale définie de\(f(x)=6x^3−4x^2+2x−3\) sur l'intervalle\([1,3]\) sous la forme de la somme de quatre intégrales définies.

Allusion

Utilisez la stratégie de résolution de l'exemple\(\PageIndex{5}\) et les propriétés des intégrales définies.

Réponse

\(\displaystyle 6∫^3_1x^3\,dx−4∫^3_1x^2\,dx+2∫^3_1x\,dx−∫^3_13\,dx \)

Exemple\(\PageIndex{6}\): Using the Properties of the Definite Integral

Si cela est connu\(\displaystyle ∫^8_0f(x)\,dx=10\) et\(\displaystyle ∫^5_0f(x)\,dx=5\), trouvez la valeur de\(\displaystyle ∫^8_5f(x)\,dx\).

Solution

Par propriété 6,

\[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx. \nonumber \]

Ainsi,

\[ \begin{align*} ∫^8_0f(x)\,dx&=∫^5_0f(x)\,dx+∫^8_5f(x)\,dx \\[4pt] 10 &=5+∫^8_5f(x)\,dx \\[4pt] 5 &=∫^8_5f(x)\,dx. \end{align*}\]

Exercice\(\PageIndex{6}\)

Si l'on sait que\(\displaystyle ∫^5_1f(x)\,dx=−3\) et\(\displaystyle ∫^5_2f(x)\,dx=4\), trouvez la valeur de\(\displaystyle ∫^2_1f(x)\,dx.\)

Allusion

Utilisez la stratégie de résolution de l'exemple\(\PageIndex{6}\) et la règle sur les propriétés des intégrales définies.

Réponse

\(−7\)

Propriétés de comparaison des intégrales

Une image peut parfois nous en dire plus sur une fonction que les résultats des calculs. La comparaison des fonctions par leurs graphes et par leurs expressions algébriques permet souvent de mieux comprendre le processus d'intégration. Intuitivement, nous pouvons dire que si une fonction\(f(x)\) est au-dessus d'une autre fonction\(g(x)\), alors l'aire entre\(f(x)\) et l'\(x\)axe -est plus grande que la zone entre\(g(x)\) et l'\(x\)axe. Cela est vrai en fonction de l'intervalle sur lequel la comparaison est effectuée. Les propriétés des intégrales définies sont valides\(a<b,\,a=b\), que ce soit ou\(a>b\). Les propriétés suivantes ne concernent toutefois que le cas\(a≤b\) et sont utilisées lorsque nous voulons comparer les tailles des intégrales.

Théorème de comparaison

i. Si c'est\(f(x)≥0\) le cas\(a≤x≤b\), alors

\[∫^b_af(x)\,dx≥0. \nonumber \]

ii. Si c'est\(f(x)≥g(x)\) le cas\(a≤x≤b\), alors

\[∫^b_af(x)\,dx≥∫^b_ag(x)\,dx. \nonumber \]

iii. Si\(m\) et\(M\) sont des constantes telles que\(m≤f(x)≤M\) pour\(a≤x≤b\), alors

\[m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]

Exemple\(\PageIndex{7}\): Comparing Two Functions over a Given Interval

Comparez\(f(x)=\sqrt{1+x^2}\) et\(g(x)=\sqrt{1+x}\) sur l'intervalle\([0,1]\).

Solution

La représentation graphique de ces fonctions est nécessaire pour comprendre comment elles se comparent au cours de l'intervalle.\([0,1].\) Au départ, lorsqu'elles sont représentées graphiquement sur une calculatrice graphique, elles\(f(x)\) semblent être au-dessus de\(g(x)\) tout. Cependant, sur l'intervalle\([0,1]\), les graphiques semblent se superposer. Nous devons zoomer pour voir cela, sur l'intervalle\([0,1],\,g(x)\) ci-dessus\(f(x)\). Les deux fonctions se croisent à\(x=0\) et\(x=1\) (Figure\(\PageIndex{8}\)).

Figure\(\PageIndex{8}\) : (a) La fonction\(f(x)\) apparaît au-dessus de la fonction\(g(x)\) sauf pendant l'intervalle\([0,1]\) (b) L'affichage du même graphique avec un zoom plus important le montre plus clairement.

Nous pouvons le voir sur le graphique sur l'intervalle\([0,1],\,g(x)≥f(x)\). En comparant les intégrales sur l'intervalle spécifié,\([0,1],\) nous le voyons également\(\displaystyle ∫^1_0g(x)\,dx≥∫^1_0f(x)\,dx\) (Figure\(\PageIndex{9}\)). La fine zone ombrée en rouge indique la différence entre ces deux intégrales au cours de l'intervalle\([0,1].\)

Figure\(\PageIndex{9}\) : (a) Le graphique montre cela sur l'intervalle\([0,1],g(x)≥f(x),\) où l'égalité ne s'applique qu'aux extrémités de l'intervalle. (b) L'affichage du même graphique avec un zoom plus important le montre plus clairement.

Valeur moyenne d'une fonction

Nous avons souvent besoin de trouver la moyenne d'un ensemble de chiffres, comme une note moyenne à un test. Supposons que vous ayez obtenu les résultats des tests suivants dans votre cours d'algèbre : 89, 90, 56, 78, 100 et 69. Votre note semestrielle est votre moyenne des résultats aux tests et vous voulez savoir à quelle note vous attendre. Nous pouvons trouver la moyenne en additionnant tous les scores et en divisant par le nombre de scores. Dans ce cas, il y a six résultats de test. Ainsi,

\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33. \nonumber \]

Par conséquent, votre note moyenne aux tests est d'environ 80,33, ce qui correspond à un B− dans la plupart des écoles.

Supposons toutefois que nous ayons une fonction\(v(t)\) qui nous donne la vitesse d'un objet à tout moment\(t\) et que nous souhaitions connaître la vitesse moyenne de l'objet. La fonction\(v(t)\) prend un nombre infini de valeurs, nous ne pouvons donc pas utiliser le processus qui vient d'être décrit. Heureusement, nous pouvons utiliser une intégrale définie pour trouver la valeur moyenne d'une telle fonction.

\(f(x)\)Soyons continus sur l'intervalle\([a,b]\) et divisent en n sous-intervalles de largeur\(Δx=(b−a)/n\).\([a,b]\) Choisissez un représentant\(x^∗_i\) dans chaque sous-intervalle et calculez\(f(x^∗_i)\) pour\(i=1,2,…,n.\) En d'autres termes, considérez chacun\(f(x^∗_i)\) comme un échantillon de la fonction sur chaque sous-intervalle. La valeur moyenne de la fonction peut ensuite être approximée comme suit :

\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}, \nonumber \]

qui est essentiellement la même expression utilisée pour calculer la moyenne des valeurs discrètes.

Mais\(Δx=\dfrac{b−a}{n},\) nous le savons\(n=\dfrac{b−a}{Δx}\) et nous obtenons

\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\left(\dfrac{b−a}{Δx}\right)}. \nonumber \]

Dans la continuité de l'algèbre, le numérateur est une somme qui est représentée\(\sum_{i=1}^nf(x∗i),\) et que nous divisons par une fraction. Pour diviser par une fraction, inversez le dénominateur et multipliez. Ainsi, une valeur approximative de la valeur moyenne de la fonction est donnée par

\[\dfrac{\sum_{i=1}^nf(x^∗_i)}{\left(\dfrac{b−a}{Δx}\right)}=\left(\dfrac{Δx}{b−a}\right)\sum_{i=1}^nf(x^∗_i)=\left(\dfrac{1}{b−a}\right)\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]

Il s'agit d'une somme de Riemann. Ensuite, pour obtenir la valeur moyenne exacte, prenez la limite\(n\) à l'infini. Ainsi, la valeur moyenne d'une fonction est donnée par

\[\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx. \nonumber \]

Définition : valeur moyenne d'une fonction

Laissez\(f(x)\) agir de manière continue pendant l'intervalle\([a,b]\). Ensuite, la valeur moyenne de la fonction\(f(x)\) (ou\(f_{ave}\)) activée\([a,b]\) est donnée par

\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)\,dx. \label{averagevalue} \]

Exemple\(\PageIndex{8}\): Finding the Average Value of a Linear Function

Trouvez la valeur moyenne de\(f(x)=x+1\) sur l'intervalle\([0,5].\)

Solution

Tout d'abord, tracez la fonction sur l'intervalle indiqué, comme indiqué sur la figure\(\PageIndex{10}\).

Figure : Le\(\PageIndex{10}\) graphique montre la zone située sous la fonction\((x)=x+1\)\([0,5].\)

La région est un trapèze situé sur le côté, nous pouvons donc utiliser la formule de surface pour un trapèze\(A=\dfrac{1}{2}h(a+b),\) où\(h\) représente la hauteur et\(a\) et\(b\) représentent les deux côtés parallèles. Ensuite,

\(\displaystyle ∫^5_0x+1\,dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}\).

Ainsi, la valeur moyenne de la fonction est

\(\displaystyle \dfrac{1}{5−0}∫^5_0x+1\,dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).

Exercice\(\PageIndex{7}\)

Trouvez la valeur moyenne de\(f(x)=6−2x\) sur l'intervalle\([0,3].\)

Allusion

Utilisez la formule de la valeur moyenne (Equation \ ref {averagevalue}) et utilisez la géométrie pour évaluer l'intégrale.

Réponse

\(3\)

Concepts clés

• L'intégrale définie peut être utilisée pour calculer la surface nette signée, qui est la surface au-dessus de l'\(x\)axe -moins l'aire au-dessous de l'\(x\)axe. La surface nette signée peut être positive, négative ou nulle.
• Les éléments constitutifs de l'intégrale définie sont l'integrand, la variable d'intégration et les limites de l'intégration.
• Les fonctions continues sur un intervalle fermé sont intégrables. Les fonctions qui ne sont pas continues peuvent tout de même être intégrables, selon la nature des discontinuités.
• Les propriétés des intégrales définies peuvent être utilisées pour évaluer les intégrales.
• L'aire sous la courbe de nombreuses fonctions peut être calculée à l'aide de formules géométriques.
• La valeur moyenne d'une fonction peut être calculée à l'aide d'intégrales définies.

Équations clés

• Intégrale définie

\(\displaystyle∫^b_af(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\)

• Propriétés de l'intégrale définie

\(\displaystyle∫^a_af(x)\,dx=0\)

\(\displaystyle∫^a_bf(x)\,dx=−∫^b_af(x)\,dx\)

\(\displaystyle∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx\)

\(\displaystyle∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx\)

\(\displaystyle∫^b_acf(x)\,dx=c∫^b_af(x)\,dx\), pour constant\(c\)

\(\displaystyle∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx\)

Lexique

valeur moyenne d'une fonction

(ou\(f_{ave})\) la valeur moyenne d'une fonction sur un intervalle peut être trouvée en calculant l'intégrale définie de la fonction et en divisant cette valeur par la longueur de l'intervalle

intégrale définie

une opération de calcul primaire ; l'aire entre la courbe et l'\(x\)axe -sur un intervalle donné est une intégrale définie

fonction intégrable

une fonction est intégrable si la limite définissant l'intégrale existe ; en d'autres termes, si la limite des sommes de Riemann\(n\) à l'infini existe

integrand

la fonction à droite du symbole d'intégration ; l'integrand inclut la fonction à intégrer

limites de l'intégration

ces valeurs apparaissent en haut et en bas du signe intégral et définissent l'intervalle sur lequel la fonction doit être intégrée

zone nette signée

l'aire située entre une fonction et l'\(x\)axe -de telle sorte que la zone située sous\(x\) l'axe -soit soustraite de la zone située au-dessus de\(x\) l'axe -; le résultat est identique à l'intégrale définie de la fonction

superficie totale

l'aire totale entre une fonction et l'\(x\)axe -est calculée en additionnant la surface au-dessus de\(x\) l'axe -et l'aire située en dessous de l'\(x\)axe -; le résultat est identique à l'intégrale définie de la valeur absolue de la fonction

variable d'intégration

indique la variable par rapport à laquelle vous intégrez ; si c'est le cas\(x\), la fonction de l'integrand est suivie de\(dx\)