5.1E : Exercices pour la section 5.1

Last updated
Save as PDF

Page ID: 197324

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.) Indiquez si les sommes données sont égales ou inégales.

$\displaystyle \sum_{i=1}^{10}i$et$\displaystyle \sum_{k=1}^{10}k$
$\displaystyle \sum_{i=1}^{10}i$et$\displaystyle \sum_{i=6}^{15}(i−5)$
$\displaystyle \sum_{i=1}^{10}i(i−1)$et$\displaystyle \sum_{j=0}^9(j+1)j$
$\displaystyle \sum_{i=1}^{10}i(i−1)$et$\displaystyle \sum_{k=1}^{10}(k^2−k)$

Réponse: a. Ils sont égaux ; ils représentent tous deux la somme des 10 premiers nombres entiers.
b. Ils sont égaux ; ils représentent tous deux la somme des 10 premiers nombres entiers.
c. Ils sont égaux en substituant$\displaystyle j=i−1.$
d. Ils sont égaux ; la première somme prend en compte les termes de la seconde.

Dans les exercices 2 à 3, utilisez les règles relatives aux sommes des puissances des nombres entiers pour calculer les sommes.

2)$\displaystyle \sum_{i=5}^{10}i$

3)$\displaystyle \sum_{i=5}^{10}i^2$

Réponse: $\displaystyle \sum_{i=5}^{10}i^2 = 385−30=355$

Supposons que$\displaystyle \sum_{i=1}^{100}a_i=15$ et$\displaystyle \sum_{i=1}^{100}b_i=−12.$

Dans les exercices 4 à 7, calculez les sommes.

4)$\displaystyle \sum_{i=1}^{100}(a_i+b_i)$

5)$\displaystyle \sum_{i=1}^{100}(a_i−b_i)$

Réponse: $\displaystyle \sum_{i=1}^{100}(a_i−b_i) = 15−(−12)=27$

6)$\displaystyle \sum_{i=1}^{100}(3a_i−4b_i)$

7)$\displaystyle \sum_{i=1}^{100}(5a_i+4b_i)$

Réponse: $\displaystyle \sum_{i=1}^{100}(5a_i+4b_i) = 5(15)+4(−12)=27$

Dans les exercices 8 à 11, utilisez les propriétés et les formules de sommation pour réécrire et évaluer les sommes.

8)$\displaystyle \sum_{k=1}^{20}100(k^2−5k+1)$

9)$\displaystyle \sum_{j=1}^{50}(j^2−2j)$

Réponse: $\displaystyle \sum_{j=1}^{50}j^2−2\sum_{j=1}^{50}j=\frac{(50)(51)(101)}{6}−\frac{2(50)(51)}{2}=40, 375$

10)$\displaystyle \sum_{j=11}^{20}(j^2−10j)$

11)$\displaystyle \sum_{k=1}^{25}[(2k)^2−100k]$

Réponse: $\displaystyle 4\sum_{k=1}^{25}k^2−100\sum_{k=1}^{25}k=\frac{4(25)(26)(51)}{9}−50(25)(26)=−10, 400$

$L_n$Dénotons la somme de l'extrémité gauche en utilisant n sous-intervalles et$R_n$ désignons la somme correspondante de l'extrémité droite.

Dans les exercices 12 à 19, calculez les sommes gauche et droite indiquées pour les fonctions données sur l'intervalle indiqué.

12)$L_4$ pour$ f(x)=\dfrac{1}{x−1}$ un$ [2,3]$

13)$ R_4$ pour$ g(x)=\cos(πx)$ un$ [0,1]$

Réponse: $R_4=0.25$

14)$ L_6$ pour$ f(x)=\dfrac{1}{x(x−1)}$ un$ [2,5]$

15)$ R_6$ pour$ f(x)=\dfrac{1}{x(x−1)}$ un$ [2,5]$

Réponse: $ R_6=0.372$

16)$ R_4$ pour$ \dfrac{1}{x^2+1}$ un$ [−2,2]$

17)$ L_4$ pour$ \dfrac{1}{x^2+1}$ un$ [−2,2]$

Réponse: $ L_4=2.20$

18)$ R_4$ pour$ x^2−2x+1$ un$ [0,2]$

19)$ L_8$ pour$ x^2−2x+1$ un$ [0,2]$

Réponse: $ L_8=0.6875$

20) Calculez les sommes de Riemann gauche et droite$ R_4$,$ L_4$ et, respectivement, pour$ f(x)=(2−|x|)$ sur$ [−2,2].$ Calculez leur valeur moyenne et comparez-la à l'aire située sous le graphique de$f$.

21) Calculez les sommes de Riemann gauche et droite$ R_6$,$ L_6$ et, respectivement, pour$ f(x)=(3−|3−x|)$ sur$ [0,6].$ Calculez leur valeur moyenne et comparez-la à l'aire sous le graphique de$f$.

Réponse: $ L_6=9.000=R_6$. Le graphique de$f$ est un triangle avec une aire$9\,\text{units}^2$.

22) Calculez les sommes de Riemann gauche$ L_4$ et droite$ R_4$, et respectivement, pour un$ f(x)=\sqrt{4−x^2}$$ [−2,2]$ et comparez leurs valeurs.

23) Calculez les sommes de Riemann gauche$ L_6$ et droite$ R_6$, et respectivement, pour un$ f(x)=\sqrt{9−(x−3)^2}$$ [0,6]$ et comparez leurs valeurs.

Réponse: $L_6=13.12899=R_6$. Ils sont égaux.

Pour les exercices 24 à 27, exprimez les sommes des points de terminaison suivants en notation sigma, mais ne les évaluez pas.

24)$ L_{30}$ pour$ f(x)=x^2$ un$ [1,2]$

25)$ L_{10}$ pour$ f(x)=\sqrt{4−x^2}$ un$ [−2,2]$

Réponse: $\displaystyle L_{10}=\frac{4}{10}\sum_{i=1}^{10}\sqrt{4−(−2+4\frac{(i−1)}{10})}$

26)$ R_{20}$ pour$ f(x)=\sin x$ un$ [0,π]$

27)$ R_{100}$ pour$\ln x$ un$[1,e]$

Réponse: $\displaystyle R_{100}=\frac{e−1}{100}\sum_{i=1}^{100}ln(1+(e−1)\frac{i}{100})$

Dans les exercices 28 à 33, tracez la fonction sous forme graphique, puis utilisez une calculatrice ou un programme informatique pour évaluer les sommes suivantes aux extrémités gauche et droite. L'aire située sous la courbe se situe-t-elle entre les sommes des extrémités gauche et droite ?

28) [T]$ L_{100}$ et$ R_{100}$ pour$ y=x^2−3x+1$ sur l'intervalle$ [−1,1]$

29) [T]$ L_{100}$ et$R_{100}$ pour$y=x^2$ sur l'intervalle$[0,1]$

Réponse

$alt$

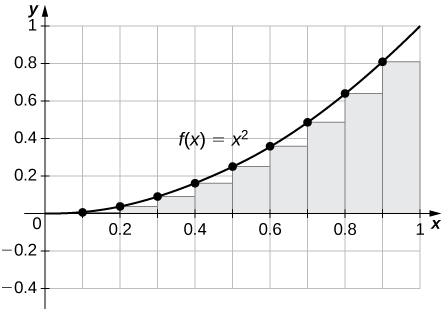
$R_{100}=0.33835,\quad L_{100}=0.32835.$
Le graphique montre que la somme de Riemann de gauche est sous-estimée car la fonction augmente. De même, la juste somme de Riemann est surestimée. La zone se situe entre les sommes de Riemann gauche et droite. Dix rectangles sont représentés pour plus de clarté visuelle. Ce comportement persiste pour d'autres rectangles.

30) [T]$L_{50}$ et$R_{50}$ pour$y=\dfrac{x+1}{x^2−1}$ sur l'intervalle$ [2,4]$

31) [T]$L_{100}$ et$R_{100}$ pour$y=x^3$ sur l'intervalle$[−1,1]$

Réponse

$alt$

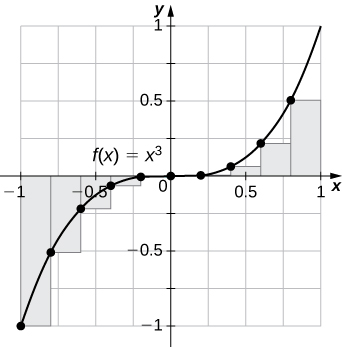
$L_{100}=−0.02,\quad R_{100}=0.02$.
La somme de l'extrémité gauche est sous-estimée car la fonction augmente. De même, une approximation du point final droit est une surestimation. La zone se situe entre les estimations des extrémités gauche et droite.

32) [T]$L_{50}$ et$R_{50}$ pour$y=\tan(x)$ sur l'intervalle$[0,\frac{π}{4}]$

33) [T]$L_{100}$ et$R_{100}$ pour$y=e^{2x}$ sur l'intervalle$[−1,1]$

Réponse

$alt$

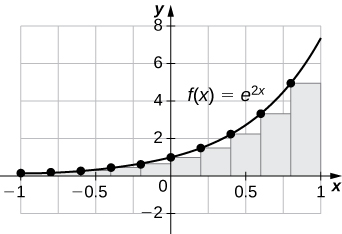
$L_{100}=3.555,\quad R_{100}=3.670$.
Le graphique montre que la somme de Riemann de gauche est sous-estimée car la fonction augmente. Dix rectangles sont représentés pour plus de clarté visuelle. Ce comportement persiste pour d'autres rectangles.

34)$t_j$ Notons le temps qu'il a fallu à Tejay van Garteren pour monter sur l'$j^\text{th}$étape du Tour de France en 2014. S'il y a un total de 21 étapes, interprétez$\displaystyle \sum_{j=1}^{21}t_j$.

35)$r_j$ Dénotons les précipitations totales à Portland le$j^\text{th}$ jour de l'année en 2009. Interpréter$\displaystyle \sum_{j=1}^{31}r_j$.

Réponse: La somme représente les précipitations cumulées en janvier 2009.

36)$d_j$ Soit les heures de lumière du jour et$ δ_j$ l'augmentation des heures de clarté d'un jour à l'autre$ j−1$ à Fargo,$j$ dans le Dakota du Nord, le$j^\text{th}$ jour de l'année. Interpré$\displaystyle d1+\sum_{j=2}^{365}δ_j.$

37) Pour se remettre en forme, Joe achète une nouvelle paire de chaussures de course. Si Joe court 1,5 km par jour au cours de la première semaine et ajoute$\dfrac{1}{10}$ un kilomètre à sa routine quotidienne chaque semaine, quel est le kilométrage total parcouru avec les chaussures de Joe après 25 semaines ?

Réponse: Le kilométrage total est de$\displaystyle 7×\sum_{i=1}^{25}(1+\frac{(i−1)}{10})=7×25+\frac{7}{10}×12×25=385$ mi.

38) Le tableau suivant donne des valeurs approximatives du taux annuel moyen d'augmentation du dioxyde de carbone (CO ₂) dans l'atmosphère chaque décennie depuis 1960, en parties par million (ppm). Estimez l'augmentation totale du CO ₂ atmosphérique entre 1964 et 2013.

Décennie	PPM/an
1964-1973	1,07
1976-1983	1,34
1984-1993	1,40
1994-2003	1,87
2004-2013	2,07

Augmentation annuelle moyenne des émissions de CO2 dans l'atmosphère, 1964—2013 Source : http://www.esrl.noaa.gov/gmd/ccgg/trends/.

39) Le tableau suivant donne l'augmentation approximative du niveau de la mer en pouces sur 20 ans à partir de l'année donnée. Estimez la variation nette du niveau moyen de la mer entre 1870 et 2010.

Année de départ	Variation sur 20 ans
1870	0,3
1890	1,5
1910	0,2
1930	2,8
1950	0,7
1970	1.1
1990	1,5

Hausse approximative du niveau de la mer sur 20 ans, 1870-1990

Une source : http://link.springer.com/article/10....712-011-9119-1

Réponse: Additionnez les chiffres pour obtenir une augmentation nette de 8,1 pouces.

40) Le tableau suivant donne l'augmentation approximative en dollars du prix moyen d'un gallon d'essence par décennie depuis 1950. Si le prix moyen d'un gallon d'essence en 2010 était de 2,60$, quel était le prix moyen d'un gallon d'essence en 1950 ?

Année de départ	Variation sur 10 ans
1950	0,03
1960	0,05
1970	0,86
1980	−0,03
1990	0,29
2000	1,12

Hausse approximative du prix du gaz sur 10 ans, 1950-2000

Source : EPB.LBL.gov/Homepages/RICK_DI... 011-trends.pdf.

41) Le tableau suivant indique le pourcentage de croissance de la population américaine à partir de juillet de l'année indiquée. Si la population des États-Unis était de 281 421 906 personnes en juillet 2000, estimez la population des États-Unis en juillet 2010.

Année	% de variation par année
2000	1,12
2001	0,99
2002	0,93
2003	0,86
2004	0,93
2005	0,93
2006	0,97
2007	0,96
2008	0,95
2009	0,88

Croissance annuelle en pourcentage de la population des États-Unis, 2000—2009

Source : www.census.gov/popest/data.

(Conseil : Pour obtenir la population en juillet 2001, multipliez la population de juillet 2000 par 1,0112 pour obtenir 284 573 831.)

Réponse: 309 389 957

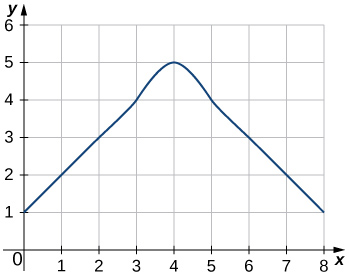
Dans les exercices 42 à 45, estimez les aires situées sous les courbes en calculant les sommes de Riemann gauches,$L_8.$

42)

$alt$

43)

$alt$

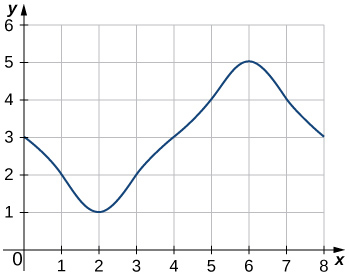
Réponse: $L_8=3+2+1+2+3+4+5+4=24$

44)

$alt$

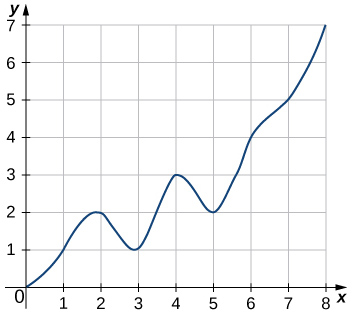
45)

$alt$

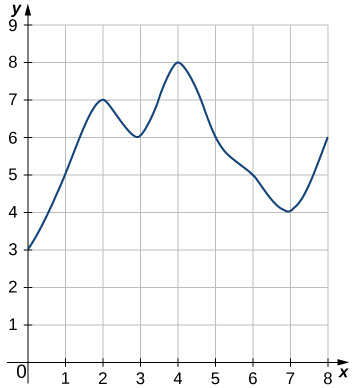
Réponse: $L_8=3+5+7+6+8+6+5+4=44$

46) [T] Utiliser un système d'algèbre informatique pour calculer la somme de Riemann$ L_N$,,$ N=10,30,50$ pour pour$ f(x)=\sqrt{1−x^2}$$[−1,1].$

47) [T] Utiliser un système d'algèbre informatique pour calculer la somme de Riemann$L_N$,,$N=10,30,50$ pour pour$f(x)=\dfrac{1}{\sqrt{1+x^2}}$$[−1,1].$

Réponse: $L_{10}≈1.7604,\quad L_{30}≈1.7625,\quad L_{50}≈1.76265$

48) [T] Utilisez un système d'algèbre informatique pour calculer la somme de Riemann,$L_N$, pour$N=10,30,50$ pour$f(x)=\sin^2 x$ on$ [0,2π]$. Comparez ces estimations avec$π$.

Dans les exercices 49 à 50, utilisez une calculatrice ou un programme informatique pour évaluer les sommes$R_N$ et$L_N$ pour les points de terminaison$N=1,10,100$. Comment ces estimations se comparent-elles aux réponses exactes que vous pouvez trouver grâce à la géométrie ?

49) [T]$y=\cos(πx)$ sur l'intervalle$[0,1]$

Réponse: $R_1=−1,\quad L_1=1,$
$R_{10}=−0.1,\quad L_{10}=0.1,$
$L_{100}=0.01,\quad R_{100}=−0.01.$
Par symétrie du graphe, l'aire exacte est nulle.

50) [T]$y=3x+2$ sur l'intervalle$[3,5]$

Dans les exercices 51 à 52, utilisez une calculatrice ou un programme informatique pour évaluer les sommes finales$R_N$ et$L_N$ pour$N=1,10,100.$

51) [T]$y=x^4−5x^2+4$ sur l'intervalle$[−2,2]$, qui a une aire exacte de$\frac{32}{15}$

Réponse: $R_1=0,\quad L_1=0,$
$R_{10}=2.4499,\quad L_{10}=2.4499,$
$R_{100}=2.1365,\quad L_{100}=2.1365$

52) [T]$y=\ln x$ sur l'intervalle$[1,2]$, qui a une aire exacte de$2\ln(2)−1$

53) Expliquez pourquoi, si$f(a)≥0$ et$f$ augmente$[a,b]$, l'estimation de l'extrémité gauche est une limite inférieure pour la zone située sous le graphique de$f$$ [a,b].$

Réponse: S'il s'$[c,d]$agit d'un sous-intervalle$ [a,b]$ inférieur à l'un des rectangles de somme de l'extrémité gauche, alors la surface du rectangle contribuant à l'estimation de l'extrémité gauche est de$ f(c)(d−c)$. Mais,$f(c)≤f(x)$ pour$c≤x≤d$, la zone sous le graphique$f$ comprise entre$c$ et$d$ est$f(c)(d−c)$ plus la zone située en dessous du graphique$f$ mais au-dessus du segment de ligne horizontale en hauteur$f(c)$, ce qui est positif. Comme cela est vrai pour chaque intervalle de somme de l'extrémité gauche, il s'ensuit que la somme de Riemann gauche est inférieure ou égale à l'aire située sous le graphique de$f$$[a,b].$

54) Expliquez pourquoi, si$f(b)≥0$ et f est décroissant, l'estimation de l'extrémité gauche est une limite supérieure pour la zone située sous le graphique de$ [a,b],$$f$$ [a,b].$

55) Montrer que, d'une manière générale,$ R_N−L_N=(b−a)×\dfrac{f(b)−f(a)}{N}.$

Réponse: $\displaystyle L_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i−1}{N})=\frac{b−a}{N}\sum_{i=0}^{N−1}f(a+(b−a)\frac{i}{N})$et$\displaystyle R_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i}{N})$. La somme de gauche a un terme correspondant à$i=0$ et la somme de droite a un terme correspondant à$i=N$. Dans$R_N−L_N$, tout terme correspondant à$i=1,2,…,N−1$ apparaît une fois avec un signe plus et une fois avec un signe moins, de sorte que chacun de ces termes est annulé et il en reste un avec$R_N−L_N=\dfrac{b−a}{N}(f(a+(b−a))\dfrac{N}{N})−(f(a)+(b−a)\dfrac{0}{N})=\dfrac{b−a}{N}(f(b)−f(a)).$

56) Expliquez pourquoi, si elle$f$ augmente$[a,b]$, l'erreur entre$L_N$ ou$R_N$ et la zone située$A$ sous le graphique de$f$ est tout au plus$(b−a)\dfrac{f(b)−f(a)}{N}$.

57) Pour chacun des trois graphiques :

a. Obtenez une limite inférieure$L(A)$ pour l'aire délimitée par la courbe en ajoutant les aires des carrés complètement délimités par la courbe.

b. Obtenez une limite supérieure$U(A)$ pour l'aire en ajoutant$L(A)$ aux aires$B(A)$ des carrés partiellement délimités par la courbe.

$alt$

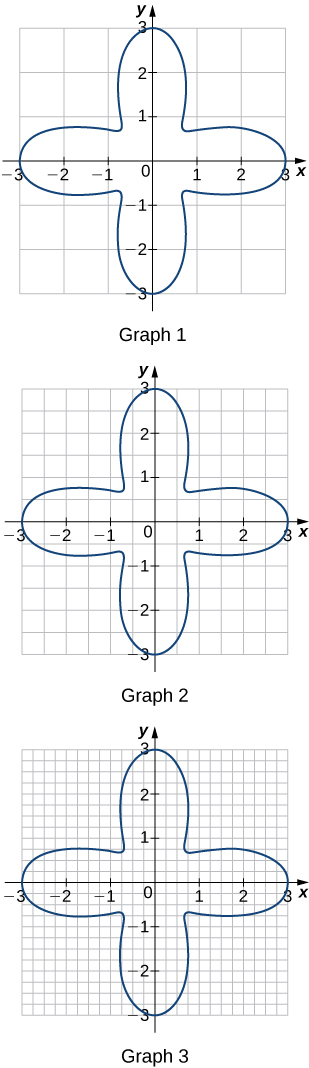
Réponse: Graphique 1 : a.$L(A)=0,\quad B(A)=20; \quad b. U(A)=20.$
Graphique 2 :$a. L(A)=9; \quad b. B(A)=11,\quad U(A)=20.$
graphique 3 : a.$ L(A)=11.0; \quad b. B(A)=4.5,\quad U(A)=15.5.$

58) Dans l'exercice précédent, expliquez pourquoi$ L(A)$ les carrés ne sont pas plus petits alors qu'ils ne$U(A)$ s'agrandissent pas lorsque les carrés sont subdivisés en quatre cases de surface égale.

59) Un cercle unitaire est composé de n coins équivalents au coin intérieur de la figure. La base du triangle intérieur est de 1 unité et sa hauteur est$\sin(\frac{π}{n}).$ La base du triangle extérieur est$B=\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})$ et la hauteur est$H=B\sin(\frac{2π}{n})$. Utilisez ces informations pour faire valoir que l'aire d'un cercle unitaire est égale à$π.$

$alt$

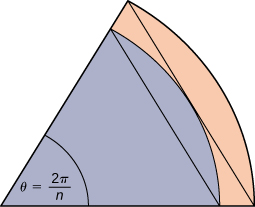
Réponse: $A$Soit l'aire du cercle unitaire. Le cercle entoure des triangles$n$ congruents de chaque zone$\dfrac{\sin(\dfrac{2π}{n})}{2}$, donc de$\frac{n}{2}\sin(\frac{2π}{n})≤A.$ même, le cercle est contenu à l'intérieur de triangles$n$ congruents de chaque zone$\dfrac{BH}{2}=\frac{1}{2}(\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n}))\sin(\frac{2π}{n})$, donc$ A≤\frac{n}{2}\sin(\frac{2π}{n})(\cos(\frac{π}{n}))+\sin(\frac{π}{n})\tan(\frac{π}{n})$. Comme c'est$n→∞,\quad \frac{n}{2}\sin(\frac{2π}{n})=\frac{π\sin(\frac{2π}{n})}{(\frac{2π}{n})}→π$ le cas, nous concluons$π≤A$. De plus$ n→∞,\quad \cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})→1$, comme nous l'avons fait aussi$A≤π$. Par le théorème de compression des limites, nous concluons que$A=π.$