5.1 : Zones approximatives

Last updated
Save as PDF

Page ID: 197316

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Utilisez la notation sigma (sommation) pour calculer les sommes et les puissances des nombres entiers.
Utilisez la somme des zones rectangulaires pour obtenir une valeur approximative de l'aire sous une courbe.
Utilisez les sommes de Riemann pour estimer la superficie.

Archimède était fasciné par le calcul des surfaces de différentes formes, c'est-à-dire de la quantité d'espace délimitée par la forme. Il a utilisé un procédé connu sous le nom de méthode d'épuisement, qui utilisait des formes de plus en plus petites, dont les surfaces pouvaient être calculées exactement, pour remplir une région irrégulière et ainsi obtenir des approximations de plus en plus proches de la surface totale. Dans ce processus, une zone délimitée par des courbes est remplie de rectangles, de triangles et de formes avec des formules de surface exactes. Ces zones sont ensuite additionnées pour obtenir une superficie approximative de la région incurvée.

Dans cette section, nous développons des techniques pour approximer l'aire entre une courbe, définie par une fonction,$f(x),$ et l'axe X sur un intervalle fermé.$[a,b].$ Comme Archimède, nous approximons d'abord l'aire sous la courbe en utilisant des formes d'aires connues (à savoir des rectangles). En utilisant des rectangles de plus en plus petits, nous obtenons des approximations de plus en plus proches de la zone. La prise d'une limite nous permet de calculer l'aire exacte sous la courbe.

Commençons par introduire quelques notations pour faciliter les calculs. Nous examinons ensuite le cas où$f(x)$ est continu et non négatif. Plus loin dans le chapitre, nous assouplissons certaines de ces restrictions et développons des techniques qui s'appliquent à des cas plus généraux.

Notation Sigma (sommation)

Comme nous l'avons mentionné, nous utiliserons des formes d'une zone connue pour approximer l'aire d'une région irrégulière délimitée par des courbes. Ce processus nécessite souvent d'additionner de longues chaînes de nombres. Pour faciliter l'écriture de ces longues sommes, nous examinons ici une nouvelle notation, appelée notation sigma (également connue sous le nom de notation de sommation). La lettre majuscule grecque$Σ$, sigma, est utilisée pour exprimer de longues sommes de valeurs sous une forme compacte. Par exemple, si nous voulons ajouter tous les entiers de 1 à 20 sans notation sigma, nous devons écrire

\[1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20. \nonumber \]

Nous pourrions probablement éviter d'écrire quelques termes et écrire

\[1+2+3+4+⋯+19+20, \nonumber \]

ce qui est mieux, mais qui reste encombrant. Avec la notation sigma, nous écrivons cette somme comme

\[\sum_{i=1}^{20}i \nonumber \]

qui est beaucoup plus compact. Généralement, la notation sigma est présentée sous la forme

\[\sum_{i=1}^{n}a_i \nonumber \]

où$a_i$ décrit les termes à ajouter, et s'$i$appelle le$index$. Chaque terme est évalué, puis nous additionnons toutes les valeurs, en commençant par la valeur quand$i=1$ et en terminant par la valeur où$i=n.$ Par exemple, une expression comme$\displaystyle \sum_{i=2}^{7}s_i$ est interprétée comme$s_2+s_3+s_4+s_5+s_6+s_7$. Notez que l'indice est utilisé uniquement pour suivre les termes à ajouter ; il n'entre pas en ligne de compte dans le calcul de la somme elle-même. L'indice est donc appelé variable fictive. Nous pouvons utiliser n'importe quelle lettre pour l'index. Généralement, les mathématiciens utilisent$i, \,j, \,k, \,m$, et$n$ pour les indices.

Essayons quelques exemples d'utilisation de la notation sigma.

Exemple$\PageIndex{1}$: Using Sigma Notation

Écrivez en notation sigma et évaluez la somme des termes$3^i$ pour$i=1,2,3,4,5.$
Ecrivez la somme en notation sigma :

\[1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}. \nonumber \]

Solution

Écrire\[\sum_{i=1}^{5}3^i=3+3^2+3^3+3^4+3^5=363. \nonumber \]
Le dénominateur de chaque terme est un carré parfait. En utilisant la notation sigma, cette somme peut être écrite sous la forme$\displaystyle \sum_{i=1}^5\dfrac{1}{i^2}$.

Exercice$\PageIndex{1}$

Écrivez en notation sigma et évaluez la somme des termes$2^i$ pour$i=3,4,5,6.$

Allusion: Utilisez les étapes de résolution de$\PageIndex{1}$ l'exemple comme guide.

Réponse: $\displaystyle \sum_{i=3}^{6}2^i=2^3+2^4+2^5+2^6=120$

Les propriétés associées au processus de sommation sont données dans la règle suivante.

Règle : Propriétés de la notation Sigma

Supposons$a_1,a_2,…,a_n$ et$b_1,b_2,…,b_n$ représentez deux séquences de termes et$c$ soyez une constante. Les propriétés suivantes sont valables pour tous les entiers positifs$n$ et pour les entiers$m$, avec$1≤m≤n.$

$\displaystyle \sum_{i=1}^n c=nc$
$\displaystyle \sum_{i=1}^n ca_i=c\sum_{i=1}^na_i$
$\displaystyle \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^n(a_i−b_i)=\sum_{i=1}^na_i−\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^na_i=\sum_{i=1}^ma_i+\sum_{i=m+1}^na_i$

Une preuve

Nous prouvons les propriétés (ii.) et (iii.) ici, et laissons la preuve des autres propriétés aux exercices.

(ii.) Nous avons

\[\sum_{i=1}^nca_i=ca_1+ca_2+ca_3+⋯+ca_n=c(a_1+a_2+a_3+⋯+a_n)=c\sum_{i=1}^na_i. \nonumber \]

(iii.) Nous avons

\[ \begin{align} \sum_{i=1}^{n}(a_i+b_i) &=(a_1+b_1)+(a_2+b_2)+(a_3+b_3)+⋯+(a_n+b_n) \\[4pt] &=(a_1+a_2+a_3+⋯+a_n)+(b_1+b_2+b_3+⋯+b_n) \\[4pt] &=\sum_{i=1}^na_i+\sum_{i=1}^nb_i. \end {align} \nonumber \]

□

Quelques formules supplémentaires pour les fonctions fréquemment trouvées simplifient davantage le processus de sommation. Ils sont présentés dans la règle suivante, pour les sommes et les puissances des nombres entiers, et nous les utilisons dans la série d'exemples suivante.

Règle : Sommes et puissances des nombres entiers

1. La somme des$n$ nombres entiers est donnée par

\[\sum_{i=1}^n i=1+2+⋯+n=\dfrac{n(n+1)}{2}. \label{sum1} \]

2. La somme des entiers consécutifs au carré est donnée par

\[\sum_{i=1}^n i^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6}. \label{sum2} \]

3. La somme des nombres entiers consécutifs au cube est donnée par

\[\sum_{i=1}^n i^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4}. \label{sum3} \]

Exemple$\PageIndex{2}$: Evaluation Using Sigma Notation

Écrivez en utilisant la notation sigma et évaluez :

La somme des termes$(i−3)^2$ pour$i=1,2,…,200.$
La somme des termes$(i^3−i^2)$ pour$i=1,2,3,4,5,6$

Solution

a. En multipliant$(i−3)^2$, on peut diviser l'expression en trois termes.

\ [\ begin {align*} \ sum_ {i=1} ^ {200} (i−3) ^2 &= \ sum_ {i=1} ^ {200} (i^2−6i+9) \ \ [4 points]
&= \ sum_ {i=1} ^ {200} i^2− \ sum_ {i=1} ^ {200} 6i+ \ sum_ {i=1} ^ {200} 6i+ \ sum_ {i=1} =1} ^ {200} 9 \ \ [4 points]
&= \ sum_ {i=1} ^ {200} i^2−6 \ sum_ {i=1} ^ {200} i+ \ sum_ {i=1} ^ {200} 9 \ \ [4 points]
&= \ dfrac {200 (200+1) (400+1)} {6} −6 \ left [\ dfrac {200 (200+1)} {2} \ droite] +9 (200) \ \ [4 points]
&=2 686 700−120 600+1800 \ \ [4 points]
&=2 567 900 \ end {align*} \]

b. Utilisez la propriété de notation sigma iv. et les règles relatives à la somme des termes au carré et à la somme des termes cubiques.

\ [\ begin {align*} \ sum_ {i=1} ^ {6} (i^3−i^2) &= \ sum_ {i=1} ^6 i^3− \ sum_ {i=1} ^6 i^2 \ \ [4 points]
&= \ dfrac {6^2 (6+1) ^2} {4} − \ dfrac {6 (6+1) (2 (6) +1)} {6} \ \ [4 points]
&= \ dfrac {1764} {4} − \ dfrac {546} {6} \ \ [4 points]
&=350 \ end {align*} \ nonnumber \]

Exercice$\PageIndex{2}$

Trouve la somme des valeurs de$4+3i$ pour$i=1,2,…,100.$

Allusion: Utilisez les propriétés de la notation sigma pour résoudre le problème.

Réponse: $15,550$

Exemple$\PageIndex{3}$: Finding the Sum of the Function Values

Trouvez la somme des valeurs de$f(x)=x^3$ sur les entiers$1,2,3,…,10.$

Solution

En utilisant l'équation \ ref {sum3}, nous avons

\[\sum_{i=0}^{10}i^3=\dfrac{(10)^2(10+1)^2}{4}=\dfrac{100(121)}{4}=3025 \nonumber \]

Exercice$\PageIndex{3}$

Evaluez la somme indiquée par la notation$\displaystyle \sum_{k=1}^{20}(2k+1)$.

Allusion: Utilisez la règle sur la somme et les puissances des nombres entiers (équations \ ref {sum1} - \ ref {sum3}).

Réponse: $440$

Surface approximative

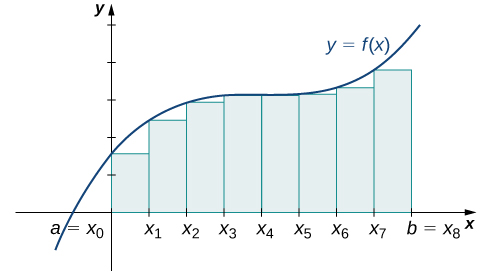
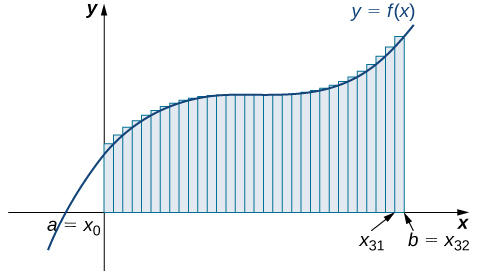
Maintenant que nous avons la notation nécessaire, nous revenons au problème qui se pose : approximer l'aire sous une courbe. $f(x)$Soit une fonction continue et non négative définie sur l'intervalle fermé$[a,b]$. Nous voulons approximer la zone$A$ délimitée par le$f(x)$ haut,$x$ l'axe -en dessous,$x=a$ la ligne de gauche et la ligne$x=b$ de droite (Figure$\PageIndex{1}$).

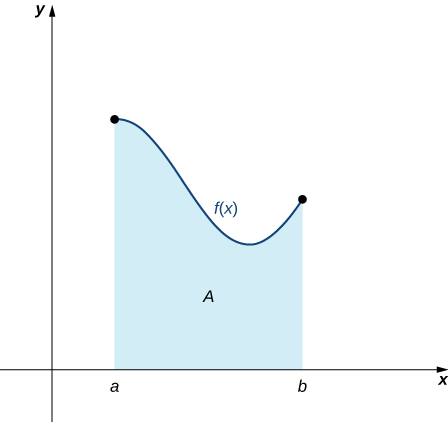
Un graphique dans le premier quadrant d'une aire délimitée par une courbe générique f (x) en haut, l'axe x en bas, la ligne x = a vers la gauche et la droite x = b vers la droite. À peu près à mi-chemin, la concavité passe de concave vers le bas à concave vers le haut, et la fonction commence à augmenter peu de temps avant la ligne x = b. — Figure$\PageIndex{1}$ : zone (zone ombrée) délimitée par la courbe en$f(x)$ haut, l'$x$axe -en bas, la ligne$x=a$ à gauche et la ligne$x=b$ à droite.

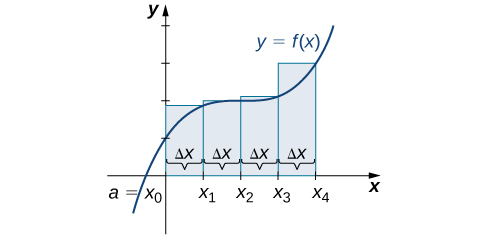
Comment approximons-nous l'aire sous cette courbe ? L'approche est géométrique. En divisant une région en de nombreuses petites formes dont les formules de surface sont connues, nous pouvons additionner ces surfaces et obtenir une estimation raisonnable de la surface réelle. Nous commençons par diviser l'intervalle$[a,b]$ en$n$ sous-intervalles de largeur égale,$\dfrac{b−a}{n}$. Pour ce faire, nous sélectionnons des points équidistants$x_0,x_1,x_2,…,x_n$ avec$x_0=a,x_n=b,$ et

\[x_i−x_{i−1}=\dfrac{b−a}{n} \nonumber \]

pour$i=1,2,3,…,n.$

Nous désignons la largeur de chaque sous-intervalle avec la notation$Δx,$ so$Δx=\frac{b−a}{n}$ et

\[x_i=x_0+iΔx \nonumber \]

pour$i=1,2,3,…,n.$ Cette notion de division d'un intervalle$[a,b]$ en sous-intervalles en sélectionnant des points à l'intérieur de l'intervalle est assez souvent utilisée pour approximer l'aire sous une courbe. Définissons donc une terminologie pertinente.

Définition : Partitions

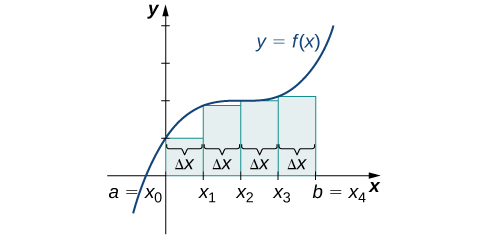
Un ensemble de points$P={x_i}$ pour$i=0,1,2,…,n$ avec$a=x_0 < x_1 < x_2 < ... < x_n = b$, qui divise l'intervalle$[a, b]$ en sous-intervalles du formulaire,$[x_0, x_1], [x_1, x_2], ..., [x_{n-1}, x_n]$ est appelépartition de$[a,b]$. Si les sous-intervalles ont tous la même largeur, l'ensemble de points forme une partition régulière (ou une partition uniforme) de l'intervalle$[a,b].$

Nous pouvons utiliser cette partition régulière comme base d'une méthode d'estimation de l'aire sous la courbe. Nous examinons ensuite deux méthodes : l'approximation de l'extrémité gauche et l'approximation de l'extrémité droite.

Règle : approximation de l'extrémité gauche

Sur chaque sous-intervalle$[x_{i−1},x_i]$ (pour$i=1,2,3,…,n$), construisez un rectangle dont la largeur$Δx$ et la hauteur sont égales à$f(x_{i−1})$, qui est la valeur de la fonction à l'extrémité gauche du sous-intervalle. Alors l'aire de ce rectangle est$f(x_{i−1})Δx$. En ajoutant les aires de tous ces rectangles, nous obtenons une valeur approximative pour$A$ (Figure$\PageIndex{2}$). Nous utilisons la notation$L_n$ pour indiquer qu'il s'agit d'une approximation de l'extrémité gauche de$A$ l'utilisation de$n$ sous-intervalles.

\[A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\sum_{i=1}^nf(x_{i−1})Δx \nonumber \]

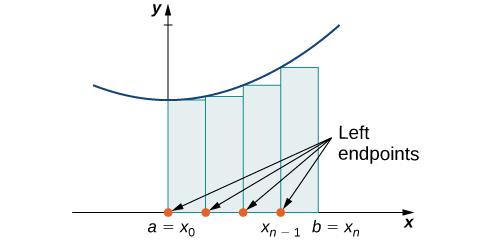
Un diagramme montrant l'approximation de l'extrémité gauche de l'aire sous une courbe. Sous une parabole dont le sommet est situé sur l'axe y et au-dessus de l'axe x, des rectangles sont dessinés entre a=x0 sur l'origine et b = xn. Les points d'extrémité des rectangles se situent à a=x0, x1, x2... x (n-1) et b = xn, espacés de manière égale. La hauteur de chaque rectangle est déterminée par la valeur de la fonction donnée à l'extrémité gauche du rectangle. — Figure$\PageIndex{2}$ : Dans l'approximation de l'extrémité gauche de l'aire sous une courbe, la hauteur de chaque rectangle est déterminée par la valeur de la fonction à gauche de chaque sous-intervalle.

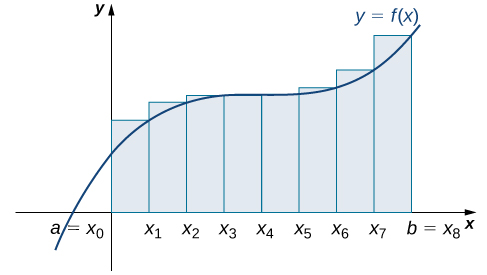
La deuxième méthode d'approximation de l'aire sous une courbe est l'approximation de l'extrémité droite. C'est presque la même chose que l'approximation de l'extrémité gauche, mais les hauteurs des rectangles sont désormais déterminées par les valeurs de la fonction à droite de chaque sous-intervalle.

Règle : approximation de l'extrémité droite

Construisez un rectangle sur chaque sous-intervalle$[x_{i−1},x_i]$, mais cette fois, la hauteur du rectangle est déterminée par la valeur de la fonction$f(x_i)$ à l'extrémité droite du sous-intervalle. Ensuite, l'aire de chaque rectangle est$f(x_i)\,Δx$ et l'approximation pour$A$ est donnée par

\[A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\sum_{i=1}^nf(x_i)Δx. \nonumber \]

La notation$R_n$ indique qu'il s'agit d'une approximation de l'extrémité droite pour$A$ (Figure$\PageIndex{3}$).

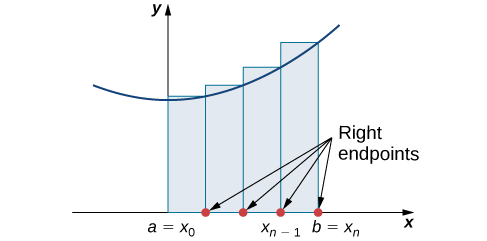
Un diagramme montrant l'approximation de l'extrémité droite de l'aire sous une courbe. Sous une parabole dont le sommet est situé sur l'axe y et au-dessus de l'axe x, des rectangles sont dessinés entre a=x0 sur l'origine et b = xn. Les points d'extrémité des rectangles se situent à a=x0, x1, x2... x (n-1) et b = xn, espacés de manière égale. La hauteur de chaque rectangle est déterminée par la valeur de la fonction donnée à l'extrémité droite du rectangle. — Figure$\PageIndex{3}$ : Dans l'approximation de l'extrémité droite de l'aire sous une courbe, la hauteur de chaque rectangle est déterminée par la valeur de la fonction à droite de chaque sous-intervalle. Notez que l'approximation de l'extrémité droite diffère de l'approximation de l'extrémité gauche de la figure$\PageIndex{2}$.

Les graphiques de la figure$\PageIndex{4}$ représentent la courbe$f(x)=\dfrac{x^2}{2}$. Dans la figure,$\PageIndex{4b}$ nous divisons la région représentée par l'intervalle$[0,3]$ en six sous-intervalles, chacun ayant une largeur$0.5$. Ainsi,$Δx=0.5$. Nous formons ensuite six rectangles en traçant des lignes verticales$x_{i−1}$ perpendiculaires à l'extrémité gauche de chaque sous-intervalle. Nous déterminons la hauteur de chaque rectangle en calculant$f(x_{i−1})$ pour$i=1,2,3,4,5,6.$ Les intervalles sont$[0,0.5],[0.5,1],[1,1.5],[1.5,2],[2,2.5],[2.5,3]$. Nous trouvons l'aire de chaque rectangle en multipliant la hauteur par la largeur. Ensuite, la somme des zones rectangulaires correspond approximativement à la zone située entre$f(x)$ et l'$x$axe. Lorsque les extrémités gauches sont utilisées pour calculer la hauteur, nous avons une approximation de l'extrémité gauche. Ainsi,

\ [\ begin {align*} A≈ L_6 &= \ sum_ {i=1} ^6f (x_ {i−1}) Δx =f (x_0) ΔX+F (x_1) ΔX+F (x_2) ΔX+F (x_3) ΔX+F (x_4) ΔX+F (x_5) Δx \ \ [4pt]
&=f (0) 0,5+f (0,5) 0,5+f (1) 0,5+f (1,5) 0,5+f (2) 0,5+f (2,5) 0,5 \ \ [4 points]
et =( 0) 0,5+ (0,125) 0,5+ (0,5) 0,5+ (1,125) 0,5+ (2) 0,5+ (3,125) 0,5 \ \ [4 points] et
= 0+0,0625 +0,25+0,5625+1+1,5625 \ \ [4 points]
&=3,4375 \, \ text {unités} ^2 \ end {align*} \ nonumber \]

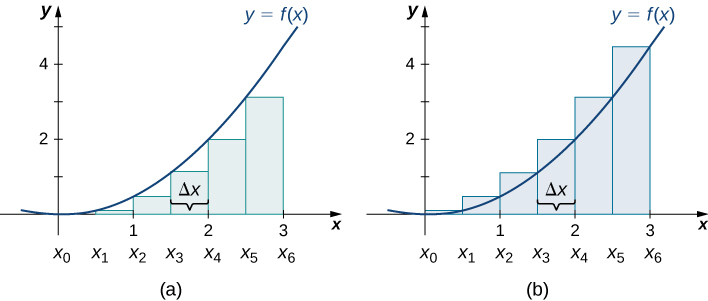
Diagrammes côte à côte, montrant les différences d'approximation de l'aire sous une courbe parabolique avec un sommet à l'origine entre la méthode des extrémités gauches (le premier diagramme) et la méthode des extrémités droites (le deuxième diagramme). Dans le premier diagramme, les rectangles sont dessinés à intervalles réguliers (delta x) sous la courbe, les hauteurs étant déterminées par la valeur de la fonction aux extrémités gauches. Dans le second diagramme, les rectangles sont dessinés de la même manière, mais avec des hauteurs déterminées par la valeur de la fonction aux extrémités droites. Les extrémités des deux sont espacées de manière égale de l'origine à (3, 0), étiquetées de x0 à x6. — Figure$\PageIndex{4}$ : Méthodes d'approximation de l'aire sous une courbe en utilisant (a) les extrémités gauche et (b) les extrémités droites.

Dans la figure$\PageIndex{4b}$, nous dessinons des lignes verticales perpendiculaires à$x_i$ l'extrémité droite de chaque sous-intervalle, et nous calculons$f(x_i)$ pour$i=1,2,3,4,5,6$.$x_i$ Nous multiplions chacune$f(x_i)$ par$Δx$ pour trouver les zones rectangulaires, puis nous les ajoutons. Il s'agit d'une approximation de l'extrémité droite de la zone située en dessous$f(x)$. Ainsi,

\ [\ begin {align*} A≈ R_6 &= \ sum_ {i=1} ^6f (x_i) ΔX=F (x_1) ΔX+F (x_2) ΔX+F (x_3) ΔX+F (x_4) ΔX+F (x_5) ΔX+F (x_6) Δx \ \ [4 points]
&=f (0,5) 0,5+f (1) 0,5+f (1,5) 0,5+f (2) 0,5+f (2,5) 0,5+f (3) 0,5 \ \ [4 points]
et =( 0,125) 0,5+ (0,5) 0,5+ (1,125) 0,5+ (2) 0,5+ (3,125) 0,5+ (4,5) 0,5 \ \ [4 points]
&=0,2506 +0,25 +0,5625+1+1,5625+2,25 \ \ [4 points]
&=5,6875 \, \ text {unités} ^2. \ end {align*} \ nonumber \]

Exemple$\PageIndex{4}$: Approximating the Area Under a Curve

Utilisez à la fois des approximations de l'extrémité gauche et de l'extrémité droite pour approximer l'aire sous la courbe de$f(x)=x^2$ sur l'intervalle$[0,2]$ ; utilisez$n=4$.

Solution

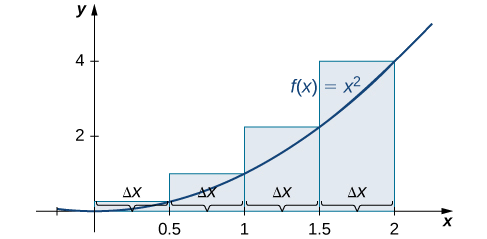
Tout d'abord, divisez l'intervalle$[0,2]$ en sous-intervalles$n$ égaux. En utilisant$n=4,\, Δx=\dfrac{(2−0)}{4}=0.5$. Il s'agit de la largeur de chaque rectangle. Les intervalles$[0,0.5],[0.5,1],[1,1.5],[1.5,2]$ sont illustrés sur la figure$\PageIndex{5}$. En utilisant une approximation de l'extrémité gauche, les hauteurs sont$f(0)=0,\,f(0.5)=0.25,\,f(1)=1,$ et$f(1.5)=2.25.$ puis,

\[ \begin{align*} L_4 &=f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+f(x_3)Δx \\[4pt] &=0(0.5)+0.25(0.5)+1(0.5)+2.25(0.5) \\[4pt] &=1.75 \,\text{units}^2 \end{align*} \nonumber \]

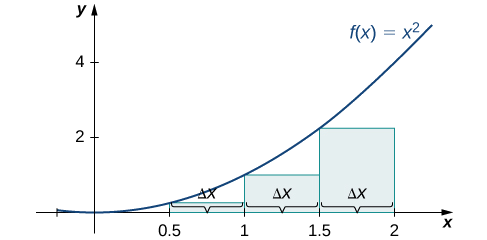
Un graphique de l'approximation de l'extrémité gauche de l'aire sous la courbe f (x) = x^2 de 0 à 2, les extrémités étant espacées de 0,5 unité. Les hauteurs du rectangle sont déterminées par les valeurs de la fonction à leur extrémité gauche. — Figure$\PageIndex{5}$ : Le graphique montre l'approximation de l'extrémité gauche de la zone située sous$f(x)=x^2$ de$0$ à$2$.

L'approximation de l'extrémité droite est illustrée sur la figure$\PageIndex{6}$. Les intervalles sont identiques,$Δx=0.5,$ mais utilisez désormais le bon point de terminaison pour calculer la hauteur des rectangles. Nous avons

\[ \begin{align*} R_4 &=f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+f(x_4)Δx \\[4pt] &=0.25(0.5)+1(0.5)+2.25(0.5)+4(0.5) \\[4pt] &=3.75 \,\text{units}^2 \end{align*} \nonumber \]

Un graphique de la méthode d'approximation de l'extrémité droite de l'aire sous la courbe f (x) = x^2 de 0 à 2, les extrémités étant espacées de 0,5 unité. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités droites. — Figure$\PageIndex{6}$ : Le graphique montre l'approximation de l'extrémité droite de la zone située en dessous$f(x)=x^2$ de$0$ à$2$.

L'approximation de l'extrémité gauche est$1.75\,\text{units}^2$ ; l'approximation de l'extrémité droite est$3.75 \,\text{units}^2$.

Exercice$\PageIndex{4}$

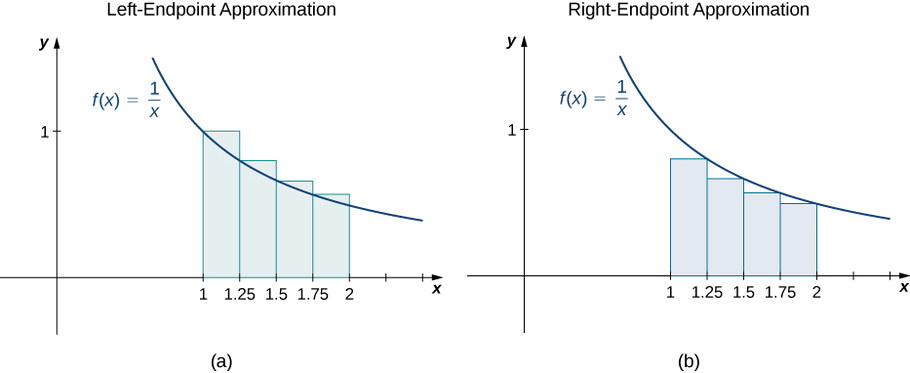
Esquissez des approximations de l'extrémité gauche et de l'extrémité$f(x)=\dfrac{1}{x}$ droite pour$[1,2]$ activer ; utilisez$n=4$. Utilisez les deux méthodes pour calculer la superficie approximative.

Allusion: Suivez la stratégie de résolution décrite dans l'exemple$\PageIndex{4}$ étape par étape.

Réponse

L'approximation de l'extrémité gauche est$0.7595 \,\text{units}^2$. L'approximation de l'extrémité droite est$0.6345 \,\text{units}^2$. Voir les médias ci-dessous.

$Deux graphiques côte à côte montrant l'approximation de l'extrémité gauche et l'approximation de l'extrémité droite de l'aire sous la courbe f (x) = 1/x de 1 à 2, les extrémités étant régulièrement espacées de 0,25 unité. Les hauteurs de l'approximation de l'extrémité gauche sont déterminées par les valeurs de la fonction aux extrémités gauches, et la hauteur de l'approximation de l'extrémité droite est déterminée par les valeurs de la fonction aux extrémités droites.$

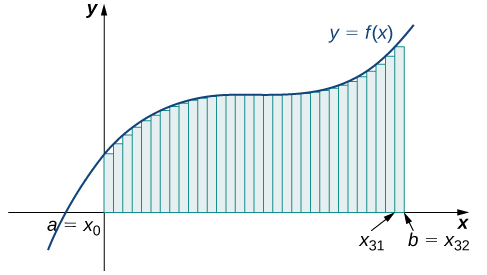
En regardant la figure$\PageIndex{4}$ et les graphiques de l'exemple$\PageIndex{4}$, nous pouvons voir que lorsque nous utilisons un petit nombre d'intervalles, ni l'approximation de l'extrémité gauche ni celle de l'extrémité droite ne constituent une estimation particulièrement précise de l'aire sous la courbe. Cependant, il semble logique que si nous augmentons le nombre de points dans notre partition, notre estimation$A$ s'améliorera. Nous aurons plus de rectangles, mais chaque rectangle sera plus fin, ce qui nous permettra d'ajuster les rectangles à la courbe avec plus de précision.

Nous pouvons démontrer l'amélioration de l'approximation obtenue par des intervalles plus petits à l'aide d'un exemple. Explorons l'idée d'augmenter$n$, d'abord dans une approximation de l'extrémité gauche avec quatre rectangles, puis huit rectangles et enfin des$32$ rectangles. Faisons ensuite la même chose dans une approximation de l'extrémité droite, en utilisant les mêmes ensembles d'intervalles, de la même région incurvée. La figure$\PageIndex{7}$ montre l'aire de la région sous la courbe$f(x)=(x−1)^3+4$ sur l'intervalle$[0,2]$ en utilisant une approximation à l'extrémité gauche où$n=4.$ La largeur de chaque rectangle est

\[Δx=\dfrac{2−0}{4}=\dfrac{1}{2}.\nonumber \]

La surface est approximée par les surfaces additionnées des rectangles, ou

\[L_4=f(0)(0.5)+f(0.5)(0.5)+f(1)(0.5)+f(1.5)0.5=7.5 \,\text{units}^2\nonumber \]

Un graphique de l'approximation de l'extrémité gauche de l'aire sous la courbe donnée, de a = x0 à b=x4. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités gauches. — Figure$\PageIndex{7}$ : Avec une approximation de l'extrémité gauche et en divisant la région de$a$ à$b$ en quatre intervalles égaux, l'aire sous la courbe est approximativement égale à la somme des aires des rectangles.

La figure$\PageIndex{8}$ montre la même courbe divisée en huit sous-intervalles. En comparant le graphique avec quatre rectangles dans la figure$\PageIndex{7}$ avec ce graphique avec huit rectangles, nous pouvons voir qu'il semble y avoir moins d'espace blanc sous la courbe lorsque$n=8.$ Cet espace blanc est une zone sous la courbe que nous ne pouvons pas inclure en utilisant notre approximation. La surface des rectangles est

\[L_8=f(0)(0.25)+f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)=7.75 \,\text{units}^2\nonumber \]

Un graphique montrant l'approximation de l'extrémité gauche de l'aire sous la courbe donnée, de a=x0 à b = x8. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités gauches. — Figure$\PageIndex{8}$ : La région située sous la courbe est divisée en zones$n=8$ rectangulaires de largeur égale pour une approximation à l'extrémité gauche.

Le graphique de la figure$\PageIndex{9}$ montre la même fonction avec$32$ des rectangles inscrits sous la courbe. Il semble qu'il reste peu d'espace blanc. La surface occupée par les rectangles est

\[L_{32}=f(0)(0.0625)+f(0.0625)(0.0625)+f(0.125)(0.0625)+⋯+f(1.9375)(0.0625)=7.9375 \,\text{units}^2.\nonumber \]

Un graphique de l'approximation de l'extrémité gauche de l'aire sous la courbe donnée, de a = x0 à b = x32. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités gauches. — Figure$\PageIndex{9}$ : Ici,$32$ des rectangles sont inscrits sous la courbe pour une approximation de l'extrémité gauche.

Nous pouvons effectuer un processus similaire pour la méthode d'approximation de l'extrémité droite. Une approximation de l'extrémité droite de la même courbe, à l'aide de quatre rectangles (Figure$\PageIndex{10}$), donne une aire

\[R_4=f(0.5)(0.5)+f(1)(0.5)+f(1.5)(0.5)+f(2)(0.5)=8.5 \,\text{units}^2.\nonumber \]

Un graphique de l'approximation de l'extrémité droite de l'aire sous la courbe donnée, de x0 à x4. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités droites. — Figure$\PageIndex{10}$ : Nous divisons maintenant l'aire sous la courbe en quatre sous-intervalles égaux pour obtenir une approximation de l'extrémité droite.

La division de la région$[0,2]$ en huit rectangles sur l'intervalle donne le résultat suivant :$Δx=\dfrac{2−0}{8}=0.25.$ Le graphique est illustré sur la figure$\PageIndex{11}$. La région est

\[R_8=f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)+f(2)(0.25)=8.25 \,\text{units}^2\nonumber \]

Un graphique de l'approximation de l'extrémité droite de l'aire sous la courbe donnée, de a=x0 à B=x8. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités droites. — Figure$\PageIndex{11}$ : Ici, nous utilisons l'approximation de l'extrémité droite pour une région divisée en huit sous-intervalles égaux.

Enfin, l'approximation de l'extrémité droite avec$n=32$ est proche de la surface réelle (Figure$\PageIndex{12}$). La superficie est d'environ

\[R_{32}=f(0.0625)(0.0625)+f(0.125)(0.0625)+f(0.1875)(0.0625)+⋯+f(2)(0.0625)=8.0625 \,\text{units}^2\nonumber \]

Un graphique de l'approximation de l'extrémité droite de l'aire sous la courbe donnée, de a=x0 à b=x32. Les hauteurs des rectangles sont déterminées par les valeurs de la fonction aux extrémités droites. — Figure$\PageIndex{12}$ : La région est divisée en sous-intervalles$32$ égaux pour une approximation de l'extrémité droite.

Sur la base de ces chiffres et de ces calculs, il semble que nous sommes sur la bonne voie ; les rectangles semblent mieux se rapprocher de l'aire sous la courbe à mesure qu'ils$n$ s'agrandissent. De plus, à mesure qu'elles$n$ augmentent, les approximations de l'extrémité gauche et de l'extrémité droite semblent s'approcher d'une surface d'unités$8$ carrées. Le tableau$\PageIndex{15}$ présente une comparaison numérique des méthodes de l'extrémité gauche et de l'extrémité droite. L'idée selon laquelle les approximations de l'aire sous la courbe s'améliorent de plus en plus à mesure que l'on$n$ s'agrandit est très importante, et nous explorons maintenant cette idée plus en détail.

Tableau$\PageIndex{15}$ : Valeurs convergentes des approximations des extrémités gauche et droite à mesure que les$n$ augmentations
Valeur de$n$	Surface approximative$L_n$	Surface approximative$R_n$
\ (n \) » style="vertical-align:middle ; « >$n=4$	\ (L_n \) » style="vertical-align:middle ; « >$7.5$	\ (R_n \) » style="vertical-align:middle ; « >$8.5$
\ (n \) » style="vertical-align:middle ; « >$n=8$	\ (L_n \) » style="vertical-align:middle ; « >$7.75$	\ (R_n \) » style="vertical-align:middle ; « >$8.25$
\ (n \) » style="vertical-align:middle ; « >$n=32$	\ (L_n \) » style="vertical-align:middle ; « >$7.94$	\ (R_n \) » style="vertical-align:middle ; « >$8.06$

Former des sommes de Riemann

Jusqu'à présent, nous avons utilisé des rectangles pour approximer l'aire sous une courbe. Les hauteurs de ces rectangles ont été déterminées en évaluant la fonction aux extrémités droite ou gauche du sous-intervalle$[x_{i−1},x_i]$. En réalité, il n'y a aucune raison de limiter l'évaluation de la fonction à l'un de ces deux points uniquement. Nous pouvons évaluer la fonction à n'importe quel point$x^∗_i$ du sous-intervalle$[x_{i−1},x_i]$ et l'utiliser$f(x^∗_i)$ comme hauteur de notre rectangle. Cela nous donne une estimation de la surface du formulaire

\[A≈\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Une somme de cette forme est appelée somme de Riemann, du nom du mathématicien du XIXe siècle Bernhard Riemann, qui a développé l'idée.

Définition : Somme de Riemann

$f(x)$Soit définie sur un intervalle fermé$[a,b]$ et$P$ soit n'importe quelle partition de$[a,b]$. $Δx_i$Soit la largeur de chaque sous-intervalle$[x_{i−1},x_i]$ et pour chacun$i$,$x^∗_i$ soit n'importe quel point à l'intérieur$[x_{i−1},\,x_i]$. Une somme de Riemann est définie$f(x)$ comme

\[\sum_{i=1}^nf(x^∗_i)\,Δx_i. \nonumber \]

À ce stade, nous allons choisir une partition normale$P$, comme nous l'avons fait dans nos exemples ci-dessus. Cela oblige tous$Δx_i$ à être égaux$Δx = \dfrac{b-a}{n}$ pour n'importe quel nombre naturel d'intervalles$n$.

Rappelez-vous qu'avec les approximations des extrémités gauche et droite, les estimations semblent s'améliorer au$n$ fur et à mesure qu'elles augmentent. Il en va de même pour les sommes Riemann. Les sommes de Riemann donnent de meilleures approximations pour des valeurs plus élevées de$n$. Nous sommes maintenant prêts à définir l'aire sous une courbe en termes de sommes de Riemann.

Définition : Aire située sous la courbe

$f(x)$Soit une fonction continue et non négative sur un intervalle$[a,b]$, et$\displaystyle \sum_{i=1}^nf(x^∗_i)\,Δx$ soit une somme de Riemann pour$f(x)$ avec une partition régulière$P$. Ensuite, l'aire sous la courbe$y=f(x)$ on$[a,b]$ est donnée par

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Voir une démonstration graphique de la construction d'une somme de Riemann.

Certaines subtilités méritent d'être discutées. Tout d'abord, notez que prendre la limite d'une somme est un peu différent de prendre la limite d'une$f(x)$ fonction$x$ à l'infini. Les limites des sommes sont abordées en détail dans le chapitre sur les séquences et les séries ; toutefois, pour l'instant, nous pouvons supposer que les techniques de calcul que nous avons utilisées pour calculer les limites des fonctions peuvent également être utilisées pour calculer les limites des sommes.

Deuxièmement, nous devons réfléchir à ce qu'il faut faire si l'expression converge vers des limites différentes pour différents choix.${x^∗_i}.$ Heureusement, cela ne se produit pas. Bien que la preuve dépasse le cadre de ce texte, on peut démontrer qu'elle$f(x)$ est continue sur l'intervalle fermé$[a,b]$, qu'elle$\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx$ existe et qu'elle est unique (en d'autres termes, elle ne dépend pas du choix de${x^∗_i}$).

Nous examinerons quelques exemples sous peu. Mais, avant de le faire, prenons un moment pour parler de certains choix spécifiques pour${x^∗_i}$. Bien que tout choix de nous${x^∗_i}$ donne une estimation de l'aire sous la courbe, nous ne savons pas nécessairement si cette estimation est trop élevée (surestimation) ou trop faible (sous-estimation). S'il est important de savoir si notre estimation est élevée ou faible, nous pouvons sélectionner notre valeur${x^∗_i}$ pour garantir un résultat ou l'autre.

Si nous voulons surestimer, par exemple, nous pouvons choisir${x^∗_i}$ cela$i=1,2,3,…,n,$$f(x^∗_i)≥f(x)$ pour tous$x∈[x_i−1,x_i]$. En d'autres termes, nous choisissons${x^∗_i}$ que for$i=1,2,3,…,n,$$f(x^∗_i)$ soit la valeur maximale de la fonction sur l'intervalle$[x_{i−1},x_i]$. Si nous sélectionnons de cette${x^∗_i}$ manière, la somme de Riemann$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$ est appelée somme supérieure. De même, si nous voulons sous-estimer, nous pouvons choisir${x∗i}$ que for$i=1,2,3,…,n,$$f(x^∗_i)$ soit la valeur minimale de la fonction sur l'intervalle$[x_{i−1},x_i]$. Dans ce cas, la somme de Riemann associée est appelée somme inférieure. Notez que si elle augmente ou$f(x)$ diminue tout au long de l'intervalle$[a,b]$, les valeurs maximale et minimale de la fonction apparaissent aux extrémités des sous-intervalles, de sorte que les sommes supérieure et inférieure sont exactement les mêmes que les approximations des extrémités gauche et droite.

Exemple$\PageIndex{5}$: Finding Lower and Upper Sums

Trouvez une somme inférieure pour$f(x)=10−x^2$ un$[1,2]$ ; laissez les$n=4$ sous-intervalles.

Solution

Avec$n=4$ plus de temps$[1,2], \,Δx=\dfrac{1}{4}$. Nous pouvons lister les intervalles au fur$[1,1.25],\,[1.25,1.5],\,[1.5,1.75],$ et à mesure$[1.75,2]$. Comme la fonction diminue au cours de l'intervalle, la$[1,2],$ figure montre qu'une somme plus faible est obtenue en utilisant les bons points d'extrémité.

Le graphique de f (x) = 10 − x^2 de 0 à 2. Il est configuré pour une approximation de l'extrémité droite de la zone délimitée par la courbe et l'axe x sur [1, 2], étiquetée a=x0 à x4. Il montre une somme plus faible. — Figure$\PageIndex{13}$ : Le graphique de$f(x)=10−x^2$ est configuré pour une approximation à l'extrémité droite de la zone délimitée par la courbe et l'$x$axe y$[1,2]$, et il montre une somme inférieure.

La somme de Riemann est

\ [\ begin {align*} \ sum_ {k=1} ^4 (10−x^2) (0,25) &=0,25 [10− (1,25) ^2+10− (1,5) ^2+10− (1,75) ^2+10− (2) ^2] \ \ [4 points] &=0,25 [8,4375+7,75+6,9375+6] \ \ [4 points]
&=0,25 [8,4375+7,75+6,9375+6] \ \ [4points] pt]
&=7,28 \, \ text {unités} ^2. \ end {align*} \]

La superficie de$7.28$$\text{units}^2$ est une somme inférieure et une sous-estimation.

Exercice$\PageIndex{5}$

Trouvez une somme supérieure pour$f(x)=10−x^2$ un$[1,2]$ ; laissez$n=4.$
Esquissez l'approximation.

Allusion: $f(x)$est décroissant$[1,2]$, de sorte que les valeurs de fonction maximales se trouvent aux extrémités gauches des sous-intervalles.

Réponse

a. Somme supérieure =$8.0313 \,\text{units}^2.$

$Un graphique de la fonction f (x) = 10 − x^2 de 0 à 2. Il est configuré pour une approximation de l'extrémité droite sur la zone [1,2], qui est étiquetée a=x0 à x4. Il s'agit d'une somme supérieure.$

Exemple$\PageIndex{6}$: Finding Lower and Upper Sums for $f(x)=\sin x$

Trouvez une somme inférieure pour l'$f(x)=\sin x$intervalle$[a,b]=\left[0,\frac{π}{2} \right]$ ; laissez$n=6.$

Solution

Examinons d'abord le graphique de la figure$\PageIndex{14}$ pour avoir une meilleure idée de la zone d'intérêt.

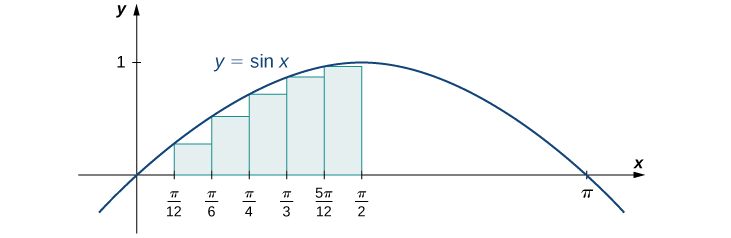
Un graphe de la fonction y = sin (x) de 0 à pi. Il est configuré pour une approximation de l'extrémité gauche comprise entre 0 et pi/2 et n = 6. Il s'agit d'une somme inférieure. — Figure$\PageIndex{14}$ : Le graphique de$y=\sin x$ est divisé en six régions :$Δx=\dfrac{π/2}{6}=\dfrac{π}{12}$.

Les intervalles sont$\left[0,\frac{π}{12}\right],\,\left[\frac{π}{12},\frac{π}{6}\right],\,\left[\frac{π}{6},\frac{π}{4}\right],\,\left[\frac{π}{4},\frac{π}{3}\right],\,\left[\frac{π}{3},\frac{5π}{12}\right]$, et$\left[\frac{5π}{12},\frac{π}{2}\right]$. Notez que cela$f(x)=\sin x$ augmente sur l'intervalle$\left[0,\frac{π}{2}\right]$, de sorte qu'une approximation de l'extrémité gauche nous donne la somme la plus faible. Une approximation de l'extrémité gauche est la somme de Riemann$\sum_{i=0}^5\sin x_i\left(\tfrac{π}{12}\right)$. Nous avons

\[A≈\sin(0)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{12}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{6}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{4}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{3}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{5π}{12}\right)\left(\tfrac{π}{12}\right)\approx 0.863 \,\text{units}^2. \nonumber \]

Exercice$\PageIndex{6}$

En utilisant la fonction$f(x)=\sin x$ sur l'intervalle,$\left[0,\frac{π}{2}\right],$ trouvez une somme supérieure ; laissez$n=6.$

Allusion: Suivez les étapes de l'exemple$\PageIndex{6}$.

Réponse: $A≈1.125 \,\text{units}^2$

Concepts clés

L'utilisation de la notation sigma (sommation) du formulaire$\displaystyle \sum_{i=1}^na_i$ est utile pour exprimer de longues sommes de valeurs sous une forme compacte.
Pour une fonction continue définie sur un intervalle,$[a,b],$ le processus qui consiste à diviser l'intervalle en parties$n$ égales, à étendre un rectangle jusqu'au graphe de la fonction, à calculer les aires de la série de rectangles, puis à additionner les aires permet d'obtenir une approximation de l'aire de cette région.
Lorsque vous utilisez une partition normale, la largeur de chaque rectangle est de$Δx=\dfrac{b−a}{n}$.
Les sommes de Riemann sont des expressions de la forme$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx,$ et peuvent être utilisées pour estimer l'aire sous la courbe Les approximations des extrémités$y=f(x).$ gauche et droite sont des types spéciaux de sommes de Riemann où les valeurs de${x^∗_i}$ sont choisies pour être les extrémités gauche ou droite des sous-intervalles, respectivement.
Les sommes de Riemann permettent une grande flexibilité dans le choix de${x^∗_i}$ l'ensemble des points auxquels la fonction est évaluée, souvent dans le but d'obtenir une somme inférieure ou supérieure.

Équations clés

Propriétés de la notation Sigma

\ [\ begin {align*} \ sum_ {i=1} ^nc&=nc \ \ [4 points]
\ sum_ {i=1} ^nca_i &=c \ sum_ {i=1} ^na_i \ \ [4 points]
\ sum_ {i=1} ^n (a_i+b_i) &= \ sum_ {i=1} ^na_i+ \ sum_ {i=1} ^nb_i \ \ [4 points]
\ sum_ {i=1} ^n (a_i−b_i) &= \ sum_ {i=1} ^na_i− \ sum_ {i=1} ^nb_i \ \ [4 points]
\ sum_ {i=1} ^na_i&= \ sum_ {i=1} ^ma_i+ \ sum_ {i=m+1} ^na_i \ end {align*} \]

Sommes et puissances des nombres entiers

\[\sum_{i=1}^ni=1+2+⋯+n=\dfrac{n(n+1)}{2} \nonumber \]

\[\sum_{i=1}^ni^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6} \nonumber \]

\[\sum_{i=0}^ni^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4} \nonumber \]

Approximation du point

$A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\displaystyle \sum_{i=1}^nf(x_{i−1})Δx$

Approximation du point

$A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\displaystyle \sum_{i=1}^nf(x_i)Δx$

Lexique

approximation de l'extrémité gauche: une approximation de l'aire sous une courbe calculée en utilisant l'extrémité gauche de chaque sous-intervalle pour calculer la hauteur des côtés verticaux de chaque rectangle

somme inférieure: une somme obtenue en utilisant la valeur minimale de$f(x)$ sur chaque sous-intervalle

partition: un ensemble de points qui divise un intervalle en sous-intervalles

partition régulière: une partition dans laquelle les sous-intervalles ont tous la même largeur

Somme de Riemann: une estimation de l'aire sous la courbe du formulaire$A≈\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$

approximation de l'extrémité droite: l'approximation de l'extrémité droite est une approximation de l'aire des rectangles sous une courbe en utilisant l'extrémité droite de chaque sous-intervalle pour construire les côtés verticaux de chaque rectangle

notation sigma: (également, notation de sommation) la lettre grecque sigma ($Σ$) indique l'addition des valeurs ; les valeurs de l'indice au-dessus et en dessous du sigma indiquent où commencer la sommation et où la terminer

somme supérieure: une somme obtenue en utilisant la valeur maximale de$f(x)$ sur chaque sous-intervalle

Valeur de\(n\)	Surface approximative\(L_n\)	Surface approximative\(R_n\)
\ (n \) » style="vertical-align:middle ; « >\(n=4\)	\ (L_n \) » style="vertical-align:middle ; « >\(7.5\)	\ (R_n \) » style="vertical-align:middle ; « >\(8.5\)
\ (n \) » style="vertical-align:middle ; « >\(n=8\)	\ (L_n \) » style="vertical-align:middle ; « >\(7.75\)	\ (R_n \) » style="vertical-align:middle ; « >\(8.25\)
\ (n \) » style="vertical-align:middle ; « >\(n=32\)	\ (L_n \) » style="vertical-align:middle ; « >\(7.94\)	\ (R_n \) » style="vertical-align:middle ; « >\(8.06\)

Exemple\(\PageIndex{1}\): Using Sigma Notation

Exercice\(\PageIndex{1}\)

Règle : Propriétés de la notation Sigma

Une preuve

Règle : Sommes et puissances des nombres entiers

Exemple\(\PageIndex{2}\): Evaluation Using Sigma Notation

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Finding the Sum of the Function Values

Exercice\(\PageIndex{3}\)

Définition : Partitions

Règle : approximation de l'extrémité gauche

Règle : approximation de l'extrémité droite

Exemple\(\PageIndex{4}\): Approximating the Area Under a Curve

Exercice\(\PageIndex{4}\)

Définition : Somme de Riemann

Définition : Aire située sous la courbe

Exemple\(\PageIndex{5}\): Finding Lower and Upper Sums

Exercice\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\): Finding Lower and Upper Sums for \(f(x)=\sin x\)

Exercice\(\PageIndex{6}\)