4.10 : Antidérivés
- Page ID
- 197671
- Détermine l'antidérivée générale d'une fonction donnée.
- Expliquez les termes et la notation utilisés pour une intégrale indéfinie.
- Définissez la règle de puissance pour les intégrales.
- Utilisez l'antidifférenciation pour résoudre des problèmes de valeur initiale simples.
À ce stade, nous avons vu comment calculer les dérivées de nombreuses fonctions et avons découvert diverses de leurs applications. Nous posons maintenant une question qui permet de renverser ce processus : étant donné une fonction\(f\), comment trouver une fonction avec la dérivée\(f\) et pourquoi nous intéresserions-nous à une telle fonction ?
Nous répondons à la première partie de cette question en définissant les antidérivés. L'antidérivée d'une fonction\(f\) est une fonction avec une dérivée\(f\). Pourquoi nous intéressons-nous aux antidérivés ? Le besoin d'antidérivés se fait sentir dans de nombreuses situations, et nous examinerons divers exemples dans le reste du texte. Nous examinons ici un exemple spécifique impliquant un mouvement rectiligne. Dans notre examen dans Dérivées du mouvement rectiligne, nous avons montré que, étant donné\(s(t)\) la fonction de position d'un objet, sa fonction de vitesse\(v(t)\) est la dérivée de\(s(t)\) — c'est-à-dire,\(v(t)=s′(t)\). De plus, l'accélération\(a(t)\) est la dérivée de la vitesse,\(v(t)\) c'est-à-dire\(a(t)=v′(t)=s''(t)\). Supposons maintenant qu'on nous donne une fonction d'accélération\(a\), mais pas la fonction de vitesse\(v\) ou la fonction de position\(s\). Puisque\(a(t)=v′(t)\), pour déterminer la fonction de vitesse, nous devons trouver une antidérivée de la fonction d'accélération. Ensuite, puisque la\(v(t)=s′(t),\) détermination de la fonction de position nous oblige à trouver une antidérivée de la fonction de vitesse. Le mouvement rectiligne n'est qu'un des cas dans lesquels le besoin d'antidérivés se fait sentir. Nous verrons de nombreux autres exemples dans la suite du texte. Pour l'instant, examinons la terminologie et la notation des antidérivés, et déterminons les antidérivés pour plusieurs types de fonctions. Nous examinerons diverses techniques permettant de trouver des antidérivés de fonctions plus complexes plus loin dans le texte (Introduction aux techniques d'intégration).
L'inverse de la différenciation
À ce stade, nous savons comment trouver les dérivées de diverses fonctions. Nous posons maintenant la question inverse. Étant donné une fonction\(f\), comment pouvons-nous trouver une fonction avec une dérivée\(f\) ? Si nous pouvons trouver une fonction\(F\) avec une dérivée,\(f,\) nous appelons\(F\) une antidérivée de\(f\).
Une fonction\(F\) est une antidérivée de la fonction\(f\) si
\[F′(x)=f(x) \nonumber \]
pour tous\(x\) dans le domaine de\(f\).
Réfléchissez à la fonction\(f(x)=2x\). Connaissant la règle de pouvoir de la différenciation, nous concluons que\(F(x)=x^2\) c'est un antidérivé du\(f\) since\(F′(x)=2x\).
Existe-t-il d'autres antidérivés de\(f\) ?
Oui ; puisque la dérivée de toute constante\(C\) est zéro, elle\(x^2+C\) est également une antidérivée de\(2x\). Par conséquent,\(x^2+5\) et\(x^2−\sqrt{2}\) sont également des antidérivés.
Y en a-t-il d'autres qui ne sont pas toujours de la forme\(x^2+C\)\(C\) ?
La réponse est non. À partir du corollaire 2 du théorème de la valeur moyenne, nous savons que si\(F\) et\(G\) sont des fonctions dérivables\(F′(x)=G′(x),\) telles que\(F(x)−G(x)=C\) pour une constante\(C\). Ce fait conduit au théorème important suivant.
\(F\)Soit un antidérivé de\(f\) plus d'un intervalle\(I\). Ensuite,
- pour chaque constante\(C\), la fonction\(F(x)+C\) est également une antidérivée de\(f\) plus\(I\) ;
- si\(G\) est une antidérivée de\(f\) over\(I\), il existe une constante\(C\) pour laquelle\(G(x)=F(x)+C\) over\(I\).
En d'autres termes, la forme la plus générale de l'antidérivé de\(f\) plus\(I\) est\(F(x)+C\).
Nous utilisons ce fait et notre connaissance des dérivés pour trouver tous les antidérivés ayant plusieurs fonctions.
Pour chacune des fonctions suivantes, trouvez tous les antidérivés.
- \(f(x)=3x^2\)
- \(f(x)=\dfrac{1}{x}\)
- \(f(x)=\cos x\)
- \(f(x)=e^x\)
Solution :
a. Parce que
\[\dfrac{d}{dx}\left(x^3\right)=3x^2 \nonumber \]
\(F(x)=x^3\)est alors un antidérivé de\(3x^2\). Par conséquent, chaque antidérivé de\(3x^2\) est de la forme\(x^3+C\) d'une constante\(C\), et chaque fonction de la forme\(x^3+C\) est une antidérivée de\(3x^2\).
b. Laissez\(f(x)=\ln |x|.\)
Pour\(x>0,\; f(x)=\ln |x|=\ln (x)\) et
\[\dfrac{d}{dx}\Big(\ln x\Big)=\dfrac{1}{x}. \nonumber \]
Pour\(x<0,\; f(x)=\ln |x|=\ln (−x)\) et
\[\dfrac{d}{dx}\Big(\ln (−x)\Big)=−\dfrac{1}{−x}=\dfrac{1}{x}. \nonumber \]
Par conséquent,
\[\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}. \nonumber \]
Ainsi,\(F(x)=\ln |x|\) est un antidérivé de\(\dfrac{1}{x}\). Par conséquent, chaque antidérivé de\(\dfrac{1}{x}\) est de la forme\(\ln |x|+C\) d'une constante\(C\) et chaque fonction de la forme\(\ln |x|+C\) est une antidérivée de\(\dfrac{1}{x}\).
c. Nous avons
\[\dfrac{d}{dx}\Big(\sin x\Big)=\cos x, \nonumber \]
\(F(x)=\sin x\)est donc un antidérivé de\(\cos x\). Par conséquent, chaque antidérivé de\(\cos x\) est de la forme\(\sin x+C\) d'une constante\(C\) et chaque fonction de la forme\(\sin x+C\) est une antidérivée de\(\cos x\).
d. Depuis
\[\dfrac{d}{dx}\left(e^x\right)=e^x, \nonumber \]
\(F(x)=e^x\)est alors un antidérivé de\(e^x\). Par conséquent, chaque antidérivé de\(e^x\) est de la forme\(e^x+C\) d'une constante\(C\) et chaque fonction de la forme\(e^x+C\) est une antidérivée de\(e^x\).
Retrouvez tous les antidérivés de\(f(x)=\sin x\).
- Allusion
-
De quelle fonction est dérivée\(\sin x\) ?
- Réponse
-
\(F(x) = −\cos x+C\)
Intégrales indéfinies
Nous examinons maintenant la notation formelle utilisée pour représenter les antidérivés et examinons certaines de leurs propriétés. Ces propriétés nous permettent de trouver des antidérivés aux fonctions plus complexes. Pour une fonction donnée\(f\), nous utilisons la notation\(f′(x)\) ou\(\dfrac{df}{dx}\) pour désigner la dérivée de\(f\). Nous introduisons ici la notation pour les antidérivés. Si\(F\) est un antidérivé de\(f\), nous disons que c'\(F(x)+C\)est l'antidérivé le plus général de\(f\) et écrivons
\[\int f(x)\,dx=F(x)+C.\nonumber \]
Le symbole\(\displaystyle \int \) est appelé signe intégral et\(\displaystyle \int f(x)\,dx\) est appelé intégrale indéfinie de\(f\).
Étant donné une fonction\(f\), l'intégrale indéfinie de\(f\), désignée
\[\int f(x)\,dx, \nonumber \]
est l'antidérivé le plus général de\(f\). Si\(F\) est un antidérivé de\(f\), alors
\[\int f(x)\,dx=F(x)+C. \nonumber \]
L'expression\(f(x)\) est appelée integrand et la variable\(x\) est la variable d'intégration.
Compte tenu de la terminologie introduite dans cette définition, le fait de trouver les antidérivés d'une fonction\(f\) est généralement appelé intégration\(f\).
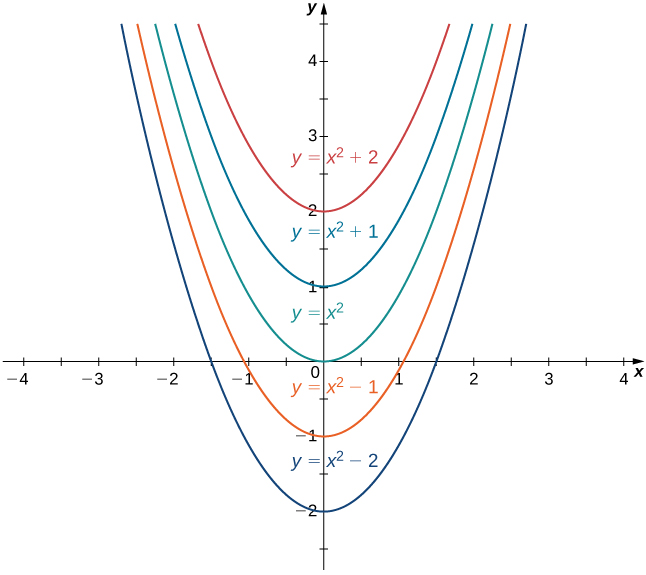
Pour une fonction\(f\) et un antidérivé\(F\), les fonctions\(F(x)+C\), où\(C\) est un nombre réel quelconque, sont souvent appelées la famille des antidérivés de\(f\). Par exemple, puisque\(x^2\) est un antidérivé de\(2x\) et tout antidérivé de\(2x\) est de la forme\(x^2+C,\) que nous écrivons
\[\int 2x\,dx=x^2+C.\nonumber \]
La collection de toutes les fonctions de la forme\(x^2+C,\) où se\(C\) trouve un nombre réel, est connue sous le nom de famille des antidérivés de\(2x\). La figure\(\PageIndex{1}\) montre un graphique de cette famille d'antidérivés.
Pour certaines fonctions, l'évaluation d'intégrales indéfinies découle directement des propriétés des dérivées. Par exemple, pour\(n≠−1\),
\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C,\)
qui provient directement de
\(\dfrac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n\).
Ce fait est connu sous le nom de règle de puissance pour les intégrales.
Pour\(n≠−1,\)
\[\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C. \nonumber \]
L'évaluation d'intégrales indéfinies pour certaines autres fonctions est également un calcul simple. Le tableau suivant répertorie les intégrales indéfinies pour plusieurs fonctions courantes. Une liste plus complète figure à l'annexe B.
| Formule de différenciation | Intégrale indéfinie |
|---|---|
| \(\dfrac{d}{dx}\Big(k\Big)=0\) | \(\displaystyle \int k\,dx=\int kx^0\,dx=kx+C\) |
| \(\dfrac{d}{dx}\Big(x^n\Big)=nx^{n−1}\) | \(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C\)pour\(n≠−1\) |
| \(\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}\) | \(\displaystyle \int \dfrac{1}{x}\,dx=\ln |x|+C\) |
| \(\dfrac{d}{dx}\Big(e^x\Big)=e^x\) | \(\displaystyle \int e^x\,dx=e^x+C\) |
| \(\dfrac{d}{dx}\Big(\sin x\Big)=\cos x\) | \(\displaystyle \int \cos x\,dx=\sin x+C\) |
| \(\dfrac{d}{dx}\Big(\cos x\Big)=−\sin x\) | \(\displaystyle \int \sin x\,dx=−\cos x+C\) |
| \(\dfrac{d}{dx}\Big(\tan x\Big)=\sec^2 x\) | \(\displaystyle \int \sec^2 x\,dx=\tan x+C\) |
| \(\dfrac{d}{dx}\Big(\csc x\Big)=−\csc x\cot x\) | \(\displaystyle \int \csc x\cot x\,dx=−\csc x+C\) |
| \(\dfrac{d}{dx}\Big(\sec x\Big)=\sec x\tan x\) | \(\displaystyle \int \sec x\tan x\,dx=\sec x+C\) |
| \(\dfrac{d}{dx}\Big(\cot x\Big)=−\csc^2 x\) | \(\displaystyle \int \csc^2x\,dx=−\cot x+C\) |
| \(\dfrac{d}{dx}\Big(\sin^{−1}x\Big)=\dfrac{1}{\sqrt{1−x^2}}\) | \(\displaystyle \int \dfrac{1}{\sqrt{1−x^2}}=\sin^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\tan^{−1}x\Big)=\dfrac{1}{1+x^2}\) | \(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\tan^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\sec^{−1}|x|\Big)=\dfrac{1}{x\sqrt{x^2−1}}\) | \(\displaystyle \int \dfrac{1}{x\sqrt{x^2−1}}\,dx=\sec^{−1}|x|+C\) |
À partir de la définition de l'intégrale indéfinie de\(f\), nous savons
\[\int f(x)\,dx=F(x)+C\nonumber \]
si et seulement si\(F\) est un antidérivé de\(f\).
Par conséquent, lorsque vous affirmez que
\[\int f(x)\,dx=F(x)+C\nonumber \]
il est important de vérifier si cette déclaration est correcte en vérifiant que\(F′(x)=f(x).\)
Chacune des déclarations suivantes est de la forme\(\displaystyle \int f(x)\,dx=F(x)+C.\) Vérifiez que chaque déclaration est correcte en montrant que\(F′(x)=f(x).\)
- \(\displaystyle\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C\)
- \(\displaystyle\int xe^x\,dx=xe^x−e^x+C\)
Solution :
a. Depuis
\(\dfrac{d}{dx}\left(\dfrac{x^2}{2}+e^x+C\right)=x+e^x\),
la déclaration
\[\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C \nonumber \]
est correct.
Notez que nous sommes en train de vérifier une intégrale indéfinie pour une somme. De plus,\(\dfrac{x^2}{2}\) et\(e^x\) sont des antidérivés de\(x\) et\(e^x\), respectivement, et la somme des antidérivés est une antidérivée de la somme. Nous reviendrons sur ce fait plus loin dans cette section.
b. En utilisant la règle du produit, nous constatons que
\[\dfrac{d}{dx}\left(xe^x−e^x+C\right)=e^x+xe^x−e^x=xe^x. \nonumber \]
Par conséquent, la déclaration
\[\int xe^x\,dx=xe^x−e^x+C \nonumber \]
est correct.
Notez que nous sommes en train de vérifier une intégrale indéfinie pour un produit. L'antidérivé n'\(xe^x−e^x\)est pas un produit des antidérivés. De plus, le produit d'antidérivés n'\(x^2e^x/2\)est pas un antidérivé de\(xe^x\) puisque
\(\dfrac{d}{dx}\left(\dfrac{x^2e^x}{2}\right)=xe^x+\dfrac{x^2e^x}{2}≠xe^x\).
En général, le produit des antidérivés n'est pas un antidérivé d'un produit.
Vérifiez que\(\displaystyle \int x\cos x\,\,dx=x\sin x+\cos x+C.\)
- Allusion
-
Calculer\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big).\)
- Réponse
-
\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big)=\sin x+x\cos x−\sin x=x \cos x\)
Dans le tableau\(\PageIndex{1}\), nous avons répertorié les intégrales indéfinies pour de nombreuses fonctions élémentaires. Passons maintenant à l'évaluation d'intégrales indéfinies pour des fonctions plus complexes. Par exemple, pensez à trouver l'antidérivée d'une somme\(f+g\). Dans l'exemple,\(\PageIndex{2}a\) nous avons montré qu'une antidérivée de la somme\(x+e^x\) est donnée par la somme, c'\(\dfrac{x^2}{2}+e^x\)est-à-dire qu'une antidérivée d'une somme est donnée par une somme d'antidérivés. Ce résultat n'était pas spécifique à cet exemple. En général, si\(F\) et\(G\) sont des antidérivés de n'importe quelle fonction\(f\) et\(g\), respectivement, alors
\(\dfrac{d}{dx}\big(F(x)+G(x)\big)=F′(x)+G′(x)=f(x)+g(x).\)
Par conséquent,\(F(x)+G(x)\) est un antidérivé de\(f(x)+g(x)\) et nous avons
\[ \int \big(f(x)+g(x)\big)\,dx=F(x)+G(x)+C.\nonumber \]
De même,
\[ \int \big(f(x)−g(x)\big)\,dx=F(x)−G(x)+C.\nonumber \]
En outre, considérez la tâche de trouver une antidérivée de l'\(kf(x),\)endroit où\(k\) se trouve un nombre réel. Depuis
\[ \dfrac{d}{dx}\Big(kF(x)\Big)=k\dfrac{d}{dx}\Big(F(x)\Big)=kF′(x)\nonumber \]
pour tout nombre réel\(k\), nous concluons que
\[ \int kf(x)\,dx=kF(x)+C.\nonumber \]
Ces propriétés sont résumées ci-dessous.
\(G\)Soit\(F\) des antidérivés de\(f\) et\(g\), respectivement, et\(k\) soit n'importe quel nombre réel.
Sommes et différences
\[\int \big(f(x)±g(x)\big)\,dx=F(x)±G(x)+C \nonumber \]
Multiples constants
\[ \int kf(x)\,dx=kF(x)+C \nonumber \]
À partir de ce théorème, nous pouvons évaluer toute intégrale impliquant une somme, une différence ou un multiple constant de fonctions avec des antidérivées connues. L'évaluation d'intégrales impliquant des produits, des quotients ou des compositions est plus complexe. (Voir Exemple\(\PageIndex{2}b\) pour un exemple impliquant un antidérivé d'un produit.) Nous examinons et abordons les intégrales impliquant ces fonctions plus complexes dans Introduction à l'intégration. Dans l'exemple suivant, nous examinons comment utiliser ce théorème pour calculer les intégrales indéfinies de plusieurs fonctions.
Évaluez chacune des intégrales indéfinies suivantes :
- \(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx\)
- \(\displaystyle \int \dfrac{x^2+4\sqrt[3]{x}}{x}\,dx\)
- \(\displaystyle \int \dfrac{4}{1+x^2}\,dx\)
- \(\displaystyle \int \tan x\cos x\,dx\)
Solution :
a. À l'aide des propriétés des intégrales indéfinies, nous pouvons intégrer séparément chacun des quatre termes de l'integrand. Nous obtenons
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx.\)
À partir de la deuxième partie de Propriétés des intégrales indéfinies, chaque coefficient peut être écrit devant le signe intégral, ce qui donne
\(\displaystyle \int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx=5\int x^3\,dx−7\int x^2\,dx+3\int x\,dx+4\int 1\,dx.\)
En utilisant la règle de puissance pour les intégrales, nous concluons que
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\dfrac{5}{4}x^4−\dfrac{7}{3}x^3+\dfrac{3}{2}x^2+4x+C.\)
b. Réécrivez l'integrand comme
\(\dfrac{x^2+4\sqrt[3]{x}}{x}=\dfrac{x^2}{x}+\dfrac{4\sqrt[3]{x}}{x}.\)
Ensuite, pour évaluer l'intégrale, intégrez chacun de ces termes séparément. En utilisant la règle du pouvoir, nous avons
\ [\ begin {align*} \ int \ left (x+ \ dfrac {4} {x^ {2/3}} \ right) \, dx&= \ int x \, dx+4 \ int x^ {−2/3} \, dx \ \ [4 points]
&= \ dfrac {1} {2} x^2+4 \ dfrac {1} {\ left (\ tfrac {−2} {3} \ right) +1} x^ {(−2/3) +1} +C \ \ [4 points]
&= \ dfrac {1} {2} x^2+12x^ {1/3} +C. \ end {align*} \]
c. En utilisant les propriétés des intégrales indéfinies, écrivez l'intégrale comme
\(4\displaystyle \int \dfrac{1}{1+x^2}\,dx.\)
Ensuite, utilisez le fait qu'il\(\tan^{−1}(x)\) s'agit d'un antidérivé de\(\dfrac{1}{1+x^2}\) pour conclure que
\(\displaystyle \int \dfrac{4}{1+x^2}\,dx=4\tan^{−1}(x)+C.\)
d. Réécrivez l'integrand comme suit :
\(\tan x\cos x=\dfrac{\sin x}{\cos x}\cdot\cos x=\sin x.\)
Par conséquent,
\(\displaystyle \int \tan x\cos x\,dx=\int \sin x\,dx=−\cos x+C.\)
Évaluer\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx\).
- Allusion
-
Intégrez chaque terme séparément dans l'integrand, en utilisant la règle de puissance.
- Réponse
-
\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx = \quad x^4−\dfrac{5}{3}x^3+\dfrac{1}{2}x^2−7x+C\)
Problèmes liés à la valeur initiale
Nous examinons les techniques permettant d'intégrer une grande variété de fonctions impliquant des produits, des quotients et des compositions plus loin dans le texte. Nous passons ici à une utilisation courante des antidérivés qui est souvent utilisée dans de nombreuses applications : la résolution d'équations différentielles.
Une équation différentielle est une équation qui met en relation une fonction inconnue et une ou plusieurs de ses dérivées. L'équation
est un exemple simple d'équation différentielle. Pour résoudre cette équation, il faut trouver une fonction\(y\) avec une dérivée\(f\). Par conséquent, les solutions de l'équation \ ref {diffeq1} sont les antidérivées de\(f\). Si\(F\) est une antidérivée de\( f\), chaque fonction de la forme\( y=F(x)+C\) est une solution de cette équation différentielle. Par exemple, les solutions de
sont donnés par
Parfois, nous cherchons à déterminer si une courbe de solution particulière passe par un certain point,\( (x_0,y_0)\) c'est-à-dire\( y(x_0)=y_0\). Le problème de la recherche d'une fonction\(y\) qui satisfait une équation différentielle
avec la condition supplémentaire
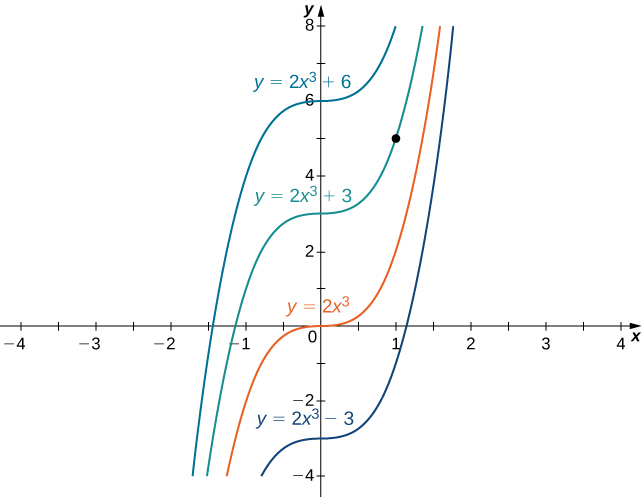
est un exemple de problème de valeur initiale. La condition\( y(x_0)=y_0\) est connue sous le nom de condition initiale. Par exemple, rechercher une fonction\( y\) qui satisfait à l'équation différentielle
et la condition initiale
est un exemple de problème de valeur initiale. Puisque les solutions de l'équation différentielle consistent\( y=2x^3+C,\) à trouver une fonction\(y\) qui satisfait également la condition initiale, nous devons trouver une\(C\) telle fonction\(y(1)=2(1)^3+C=5\). À partir de cette équation, nous voyons cela\( C=3\) et nous concluons que\( y=2x^3+3\) c'est la solution à ce problème de valeur initiale, comme le montre le graphique suivant.
Résolvez le problème de la valeur initiale
\[\dfrac{dy}{dx}=\sin x,\quad y(0)=5.\nonumber \]
Solution
Nous devons d'abord résoudre l'équation différentielle. Si\(\dfrac{dy}{dx}=\sin x\), alors
\[y=\displaystyle \int \sin(x)\,dx=−\cos x+C.\nonumber \]
Ensuite, nous devons rechercher une solution\(y\) qui réponde à la condition initiale. La condition initiale\(y(0)=5\) signifie que nous avons besoin d'une constante\(C\) telle que,\(−\cos x+C=5.\) par conséquent,
\[C=5+\cos(0)=6.\nonumber \]
La solution au problème de la valeur initiale est\(y=−\cos x+6.\)
Résolvez le problème de valeur initiale\(\dfrac{dy}{dx}=3x^{−2},\quad y(1)=2\).
- Allusion
-
Retrouvez tous les antidérivés de\(f(x)=3x^{−2.}\)
- Réponse
-
\(y=−\dfrac{3}{x}+5\)
Des problèmes de valeur initiale se posent dans de nombreuses applications. Nous examinons ensuite un problème dans lequel un conducteur freine une voiture. Nous voulons savoir combien de temps il faut à la voiture pour s'arrêter. Rappelons que la fonction de vitesse\(v(t)\) est la dérivée d'une fonction de position\(s(t),\) et que l'accélération\(a(t)\) est la dérivée de la fonction de vitesse. Dans les exemples précédents du texte, nous pouvions calculer la vitesse à partir de la position, puis calculer l'accélération à partir de la vitesse. Dans l'exemple suivant, nous travaillons dans l'autre sens. À partir d'une fonction d'accélération, nous calculons la fonction de vitesse. Nous utilisons ensuite la fonction de vitesse pour déterminer la fonction de position.
Une voiture roule à la vitesse de\(88\) pi/sec (\(60\)mi/h) lorsque les freins sont serrés. La voiture commence à décélérer à une vitesse constante de\(15\) pieds/sec 2.
- Combien de secondes s'écoulent avant que la voiture ne s'arrête ?
- Quelle est la distance parcourue par la voiture pendant cette période ?
Solution
a. Nous introduisons d'abord des variables pour ce problème. \(t\)Soit le temps (en secondes) qui s'écoule après la première application des freins. \(a(t)\)Soit l'accélération de la voiture (en pieds par seconde au carré) à la fois\(t\). \(v(t)\)Soit la vitesse de la voiture (en pieds par seconde) à la fois\(t\). \(s(t)\)Soit la position de la voiture (en pieds) au-delà du point où les freins sont actionnés à un moment donné\(t\).
La voiture roule à un rythme de\(88\) pieds par seconde. Par conséquent, la vitesse initiale est en\(v(0)=88\) pieds par seconde. Comme la voiture décélère, l'accélération est
\(a(t)=−15\,\text{ft/sec}^2\).
L'accélération est la dérivée de la vitesse,
\(v′(t)=-15.\)
Nous avons donc un problème de valeur initiale à résoudre :
\(v′(t)=−15,\quad v(0)=88.\)
En intégrant, nous constatons que
\(v(t)=−15t+C.\)
Puisque\(v(0)=88,C=88.\) Ainsi, la fonction de vitesse est
\(v(t)=−15t+88.\)
Pour savoir combien de temps il faut à la voiture pour s'arrêter, nous devons trouver le temps\(t\) tel que la vitesse soit nulle. En résolvant,\(−15t+88=0,\) nous obtenons\(t=\dfrac{88}{15}\) sec.
b. Pour déterminer la distance parcourue par la voiture pendant cette période, nous devons trouver la position de la voiture après une\(\dfrac{88}{15}\) seconde. Nous savons que la vitesse\(v(t)\) est la dérivée de la position\(s(t)\). Considérez la position initiale comme étant\(s(0)=0\). Par conséquent, nous devons résoudre le problème de la valeur initiale
\(s′(t)=−15t+88,\quad s(0)=0.\)
En nous intégrant, nous avons
\(s(t)=−\dfrac{15}{2}t^2+88t+C.\)
Depuis\(s(0)=0\), la constante est\(C=0\). Par conséquent, la fonction de position est
\(s(t)=−\dfrac{15}{2}t^2+88t.\)
Après une\(t=\frac{88}{15}\) seconde, la position est de\(s\left(\frac{88}{15}\right)≈258.133\) pieds.
Supposons que la voiture se déplace à une vitesse de\(44\) pieds par seconde. Combien de temps faut-il pour que la voiture s'arrête ? Quelle distance parcourra la voiture ?
- Allusion
-
\(v(t)=−15t+44.\)
- Réponse
-
\(2.93\)sec,\(64.5\) pieds
Concepts clés
- Si\(F\) est un antidérivé de\(f,\) alors chaque antidérivé de\(f\) est de la forme\(F(x)+C\) pour une constante\(C\).
- \[\dfrac{dy}{dx}=f(x),\quad y(x_0)=y_0 \nonumber \]Pour résoudre le problème de la valeur initiale, nous devons d'abord trouver l'ensemble des antidérivés de,\(f\) puis rechercher l'antidérivé particulier qui satisfait également à la condition initiale.
Lexique
- antidérivé
- une fonction\(F\) telle que,\(F′(x)=f(x)\) pour tous,\(x\) dans le domaine de\(f\) est une antidérivée de\(f\)
- intégrale indéfinie
- l'antidérivée la plus générale de\(f(x)\) est l'intégrale indéfinie de\(f\) ; nous utilisons la notation\(\displaystyle \int f(x)\,dx\) pour désigner l'intégrale indéfinie de\(f\)
- problème de valeur initiale
- un problème qui nécessite de trouver une fonction\(y\) qui satisfait à l'équation différentielle\(\dfrac{dy}{dx}=f(x)\) ainsi qu'à la condition initiale\(y(x_0)=y_0\)


