4.4 : Le théorème de la valeur moyenne

Last updated
Save as PDF

Page ID: 197699

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Expliquez la signification du théorème de Rolle.
Décrivez la signification du théorème de la valeur moyenne.
Énoncez trois conséquences importantes du théorème de la valeur moyenne.

Le théorème de la valeur moyenne est l'un des plus importants théorèmes du calcul. Nous examinons certaines de ses implications à la fin de cette section. Commençons par un cas particulier du théorème de la valeur moyenne, appelé théorème de Rolle.

Théorème de Rolle

De manière informelle, le théorème de Rolle indique que si les sorties d'une fonction dérivable$f$ sont égales aux extrémités d'un intervalle, il doit y avoir un point intérieur$c$ où$f'(c)=0$. La figure$\PageIndex{1}$ illustre ce théorème.

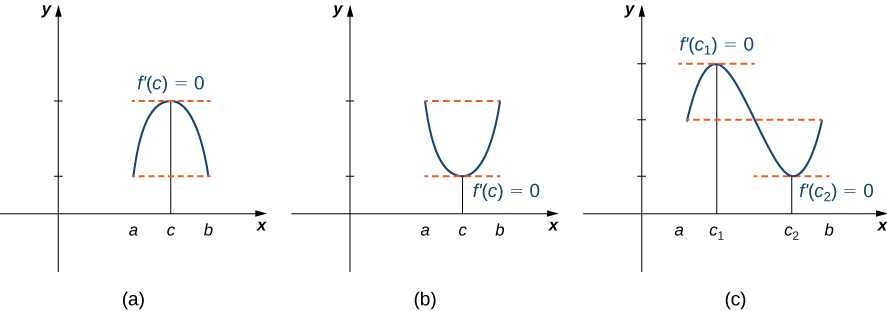
La figure est divisée en trois parties appelées a, b et c. La figure a montre le premier quadrant avec les valeurs a, c et b marquées sur l'axe des abscisses. Une parabole orientée vers le bas est dessinée de telle sorte que ses valeurs en a et en b soient identiques. Le point c est le maximum global, et on note que f' (c) = 0. La figure b montre le premier quadrant avec les valeurs a, c et b marquées sur l'axe des abscisses. Une parabole orientée vers le haut est dessinée de telle sorte que ses valeurs en a et en b soient identiques. Le point c est le minimum global, et on note que f' (c) = 0. La figure c montre le premier quadrant avec les points a, c1, c2 et b marqués sur l'axe des abscisses. Une période d'une onde sinusoïdale est tracée de telle sorte que ses valeurs en a et en b soient égales. Le point c1 est le maximum global, et on note que f' (c1) = 0. Le point c2 est le minimum global, et on note que f' (c2) = 0. — Figure$\PageIndex{1}$ : Si une fonction dérivable$f$ satisfait$f(a)=f(b)$, sa dérivée doit être nulle à certains points entre$a$ et$b$.

Théorème de Rolle

$f$Soit une fonction continue sur l'intervalle fermé$[a,b]$ et dérivable sur l'intervalle ouvert de$(a,b)$ telle sorte que$f(a)=f(b)$. Il en existe alors au moins un$c∈(a,b)$ tel que$f'(c)=0.$

Une preuve

$k=f(a)=f(b).$Considérons trois cas :

$f(x)=k$pour tous$x∈(a,b).$
Il existe$x∈(a,b)$ tel que$f(x)>k.$
Il existe$x∈(a,b)$ tel que$f(x)<k.$

Cas 1 : Si$f(x)=k$ pour tous$x∈(a,b)$, alors$f'(x)=0$ pour tous$x∈(a,b).$

Cas 2 : Comme$f$ il s'agit d'une fonction continue sur l'intervalle fermé et borné$[a,b]$, selon le théorème des valeurs extrêmes, elle a un maximum absolu. De plus, comme il existe un point$x∈(a,b)$ tel que$f(x)>k$, le maximum absolu est supérieur à$k$. Par conséquent, le maximum absolu ne se produit à aucun des deux paramètres. Par conséquent, le maximum absolu doit se produire à un point intérieur$c∈(a,b)$. Parce qu'il$f$ a un maximum à un point$c$ intérieur et qu'$f$il est différenciable à$c$, selon le théorème de Fermat,$f'(c)=0.$

Cas 3 : Le cas où il existe un point$x∈(a,b)$ analogue au cas 2, le maximum étant remplacé par le minimum.$f(x)<k$

□

Un point important du théorème de Rolle est que la différentiabilité de la fonction$f$ est critique. S'il n'$f$est pas différenciable, même en un seul point, le résultat peut ne pas être valable. Par exemple, la fonction$f(x)=|x|−1$ est continue sur$[−1,1]$ et$f(−1)=0=f(1)$, mais$f'(c)≠0$ pour tout,$c∈(−1,1)$ comme indiqué dans la figure suivante.

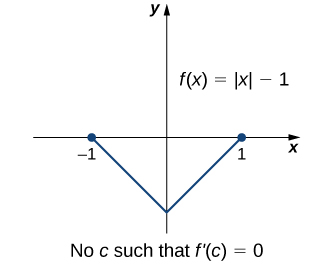
La fonction f (x) = |x| − 1 est représentée graphiquement. On montre que f (1) = f (−1), mais on remarque qu'il n'y a pas de c tel que f' (c) = 0. — Figure$\PageIndex{2}$ : Comme$f(x)=|x|−1$ il n'est pas différenciable à$x=0$, les conditions du théorème de Rolle ne sont pas satisfaites. En fait, la conclusion ne tient pas ici ; il n'existe pas de$c∈(−1,1)$ telle sorte que$f'(c)=0.$

Examinons maintenant les fonctions qui répondent aux conditions du théorème de Rolle et calculons explicitement les points$c$ où$f'(c)=0.$

Exemple$\PageIndex{1}$: Using Rolle’s Theorem

Pour chacune des fonctions suivantes, vérifiez que la fonction répond aux critères énoncés dans le théorème de Rolle et trouvez toutes les valeurs$c$ dans l'intervalle donné où$f'(c)=0.$

$f(x)=x^2+2x$terminé$[−2,0]$
$f(x)=x^3−4x$terminé$[−2,2]$

Solution

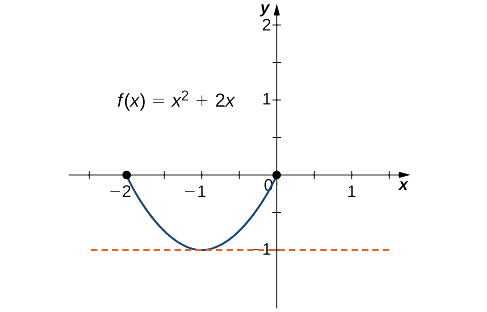
a. Comme il$f$ s'agit d'un polynôme, il est continu et différenciable partout. En outre,$f$ répond$f(−2)=0=f(0).$ donc aux critères du théorème de Rolle. Nous concluons qu'il existe au moins une valeur$c∈(−2,0)$ telle que$f'(c)=0$. Comme$f'(x)=2x+2=2(x+1),$ nous le voyons, cela$f'(c)=2(c+1)=0$ implique ce$c=−1$ que montre le graphique suivant.

La fonction f (x) = x2 +2x est représentée graphiquement. On montre que f (0) = f (−2), et une ligne horizontale en pointillés est tracée au minimum absolu en (−1, −1). — Figure$\PageIndex{3}$ : Cette fonction est continue et dérivable sur [−2,0],$f'(c)=0$ quand$c=−1$.

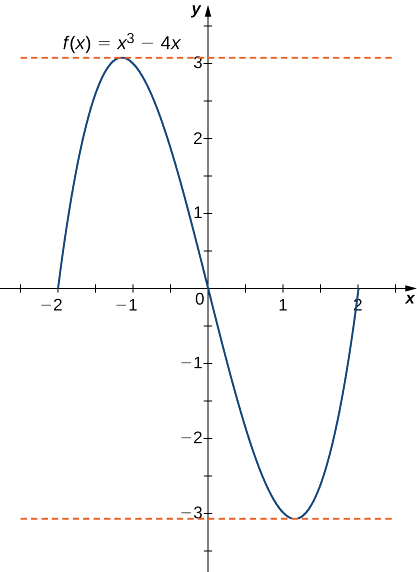
b. Comme dans la partie a.$f$ est un polynôme et est donc continu et dérivable partout. $f(−2)=0=f(2).$Cela dit,$f$ répond également aux critères du théorème de Rolle. En différenciant, nous constatons que,$f'(x)=3x^2−4.$ par conséquent,$f'(c)=0$ quand$x=±\frac{2}{\sqrt{3}}$. Les deux points se situent dans l'intervalle et$[−2,2]$, par conséquent, les deux points répondent à la conclusion du théorème de Rolle, comme le montre le graphique suivant.

La fonction f (x) = x3 — 4x est représentée graphiquement. Il est évident que f (2) = f (−2) = f (0). Les lignes horizontales en pointillés sont tracées à x = ±2/racine carrée de 3, qui sont le maximum et le minimum locaux. — Figure$\PageIndex{4}$ : Pour ce polynôme situé$[−2,2], f'(c)=0$ à$x=±2/\sqrt{3}$.

Exercice$\PageIndex{1}$

Vérifiez que la fonction$f(x)=2x^2−8x+6$ définie sur l'intervalle$[1,3]$ répond aux conditions du théorème de Rolle. Trouvez tous les points$c$ garantis par le théorème de Rolle.

Allusion: Trouvez toutes les valeurs$c$, où$f'(c)=0$.

Réponse: $c=2$

Le théorème de la valeur moyenne et sa signification

Le théorème de Rolle est un cas particulier du théorème de la valeur moyenne. Dans le théorème de Rolle, nous considérons les fonctions dérivables$f$ qui sont nulles aux extrémités. Le théorème de la valeur moyenne généralise le théorème de Rolle en considérant des fonctions qui ne sont pas nécessairement nulles aux extrémités. Par conséquent, nous pouvons considérer le théorème de la valeur moyenne comme une version inclinée du théorème de Rolle (Figure$\PageIndex{5}$). Le théorème de la valeur moyenne indique que s'il$f$ est continu sur l'intervalle fermé$[a,b]$ et dérivable sur l'intervalle ouvert$(a,b)$, il existe alors un point$c∈(a,b)$ tel que la droite tangente au graphe de$f$ at$c$ soit parallèle à la droite sécante reliant $(a,f(a))$et$(b,f(b)).$

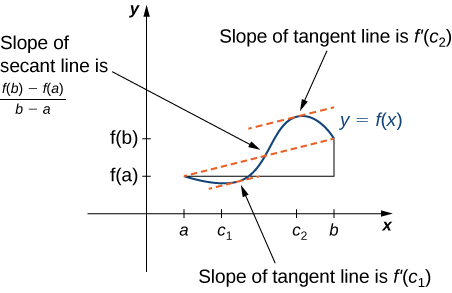
Une fonction vaguement sinusoïdale y = f (x) est dessinée. Sur l'axe X, a, c1, c2 et b sont marqués. Sur l'axe y, f (a) et f (b) sont marqués. La fonction f (x) commence à (a, f (a)), diminue jusqu'à c1, augmente jusqu'à c2, puis diminue jusqu'à (b, f (b)). Une ligne sécante est tracée entre (a, f (a)) et (b, f (b)), et on note que cette droite a une pente (f (b) — f (a))/(b − a). Les lignes tangentes en c1 et c2 sont tracées, et ces droites sont parallèles à la droite sécante. Il est à noter que les pentes de ces tangentes sont f' (c1) et f' (c2), respectivement. — Figure$\PageIndex{5}$ : Le théorème de la valeur moyenne indique que pour une fonction qui répond à ses conditions, à un moment donné, la droite tangente a la même pente que la droite sécante entre les extrémités. Pour cette fonction, il existe deux valeurs$c_1$$c_2$ telles que la tangente à$f$ at$c_1$ et$c_2$ ait la même pente que la droite sécante.

Théorème de la valeur moyenne

$f$Soit continu sur l'intervalle fermé$[a,b]$ et différenciable sur l'intervalle ouvert$(a,b)$. Il existe alors au moins un point$c∈(a,b)$ tel que

\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]

Une preuve

La preuve découle du théorème de Rolle en introduisant une fonction appropriée qui répond aux critères du théorème de Rolle. Considérez la ligne qui relie$(a,f(a))$ et$(b,f(b)).$ puisque la pente de cette ligne est

\[\frac{f(b)−f(a)}{b−a} \nonumber \]

et la droite passe par le point,$(a,f(a)),$ l'équation de cette droite peut être écrite comme

\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]

$g(x)$Dénotons la différence verticale entre le point$(x,f(x))$ et le point$(x,y)$ sur cette ligne. Par conséquent,

\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]

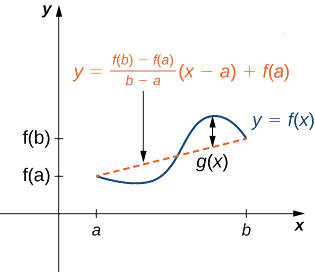$La courbe montante mais oscillante Y est égale à F de X avec la droite sécante Y égale F de B moins F de A sur toute la surface B moins A plus F de A, la distance entre la courbe oscillante et la droite est G de X$ Figure$\PageIndex{6}$ : La valeur$g(x)$ est la différence verticale entre le point$(x,f(x))$ et$(x,y)$ le point de la ligne sécante reliant$(a,f(a))$ et$(b,f(b))$.

Puisque le graphe de$f$ croise la droite sécante quand$x=a$ et$x=b$, nous voyons cela$g(a)=0=g(b)$. Puisque$f$ est une fonction dérivable sur$(a,b)$,$g$ est également une fonction dérivable sur$(a,b)$. De plus, puisque$f$ c'est continu,$[a,b], \, g$ c'est aussi continu$[a,b]$. $g$Répond donc aux critères du théorème de Rolle. Par conséquent, il existe un point$c∈(a,b)$ tel que$g'(c)=0.$ puisque

\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]

nous voyons que

\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]

Puisque$g'(c)=0,$ nous concluons que

\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

□

Dans l'exemple suivant, nous montrons comment le théorème de la valeur moyenne peut être appliqué à la fonction$f(x)=\sqrt{x}$ pendant l'intervalle$[0,9]$. La méthode est la même pour les autres fonctions, mais avec parfois des conséquences plus intéressantes.

Exemple$\PageIndex{2}$: Verifying that the Mean Value Theorem Applies

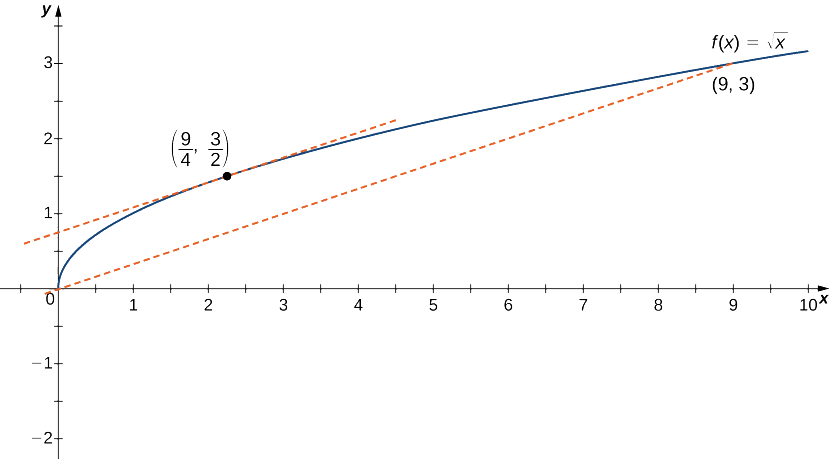
Pour l'$f(x)=\sqrt{x}$intervalle$[0,9]$, montrez que cela$f$ satisfait à l'hypothèse du théorème de la valeur moyenne, et il existe donc au moins une valeur$c∈(0,9)$ égale à la pente de la ligne reliant$(0,f(0))$ et$(9,f(9))$.$f′(c)$ Trouvez ces valeurs$c$ garanties par le théorème des valeurs moyennes.

Solution

Nous savons que$f(x)=\sqrt{x}$ c'est continu$[0,9]$ et dérivable.$(0,9).$ Par conséquent,$f$ répond aux hypothèses du théorème de la valeur moyenne, et il doit exister au moins une valeur$c∈(0,9)$ égale à la pente de la ligne reliant$(0,f(0))$ et$f′(c)$$(9,f(9))$ (Figurine$\PageIndex{7}$). Pour déterminer quelles valeurs de$c$ sont garanties, calculez d'abord la dérivée de$f$. Le dérivé$f′(x)=\frac{1}{(2\sqrt{x})}$. La pente de la ligne reliant$(0,f(0))$ et$(9,f(9))$ est donnée par

\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]

Nous voulons trouver$c$ une telle solution$f′(c)=\frac{1}{3}$. C'est-à-dire que nous voulons trouver de$c$ telle sorte que

\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]

En résolvant cette équation pour$c$, nous obtenons$c=\frac{9}{4}$. À ce stade, la pente de la tangente est égale à la pente de la ligne joignant les extrémités.

La fonction f (x) = la racine carrée de x est représentée graphiquement de (0, 0) à (9, 3). Une ligne sécante est tracée entre (0, 0) et (9, 3). Au point (9/4, 3/2), une tangente est tracée, et cette ligne est parallèle à la droite sécante. — Figure$\PageIndex{7}$ : La pente de la tangente at$c=9/4$ est identique à la pente du segment de droite reliant (0,0) et (9,3).

Une application qui permet d'illustrer le théorème de la valeur moyenne concerne la vitesse. Supposons, par exemple, que nous conduisions une voiture pendant 1 h sur une route droite avec une vitesse moyenne de 45 mi/h. Soit$s(t)$ et$v(t)$ dénotent la position et la vitesse de la voiture, respectivement, pour$0≤t≤1$ h. En supposant que la fonction de position$s(t)$ soit dérivable, nous pouvons appliquer le théorème de la valeur moyenne pour conclure qu'à un moment donné$c∈(0,1)$, la vitesse de la voiture était exactement

\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]

Exemple$\PageIndex{3}$: Mean Value Theorem and Velocity

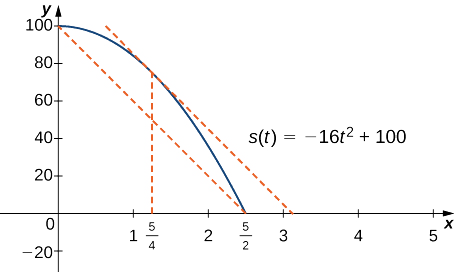
Si une pierre tombe d'une hauteur de 100 pieds, sa position$t$ quelques secondes après sa chute jusqu'à ce qu'elle touche le sol est donnée par la fonction$s(t)=−16t^2+100.$

Déterminez combien de temps il faut avant que la roche ne touche le sol.
Déterminez la vitesse moyenne$v_{avg}$ de la roche lorsque la roche est relâchée et que la roche touche le sol.
Détermine le temps$t$ garanti par le théorème de la valeur moyenne lorsque la vitesse instantanée de la roche est$v_{avg}.$

Solution

a. Lorsque le rocher touche le sol, sa position est$s(t)=0$. En résolvant l'équation$−16t^2+100=0$ pour$t$, nous trouvons que$t=±\frac{5}{2}sec$. Comme nous ne faisons que réfléchir$t≥0$, la balle touchera le sol quelques$\frac{5}{2}$ secondes après avoir été lâchée.

b. La vitesse moyenne est donnée par

\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]

c. La vitesse instantanée est donnée par la dérivée de la fonction de position. Par conséquent, nous devons trouver un temps$t$ tel que$v(t)=s′(t)=v_{avg}=−40$ ft/sec. Comme$s(t)$ il est continu sur l'intervalle$[0,5/2]$ et différenciable sur l'intervalle$(0,5/2),$ par le théorème de la valeur moyenne, il est garanti qu'il y ait un point$c∈(0,5/2)$ tel que

\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]

En prenant la dérivée de la fonction de position$s(t)$, nous constatons que,$s′(t)=−32t.$ par conséquent, l'équation se réduit à$s′(c)=−32c=−40.$ résoudre cette équation pour$c$, nous avons$c=\frac{5}{4}$. Ainsi, une$\frac{5}{4}$ seconde après la chute de la roche, la vitesse instantanée est égale à la vitesse moyenne de la roche lors de sa chute libre :$−40$ pieds par seconde.

La fonction s (t) = −16t2 + 100 est représentée graphiquement de (0, 100) à (5/2, 0). Une ligne sécante est tracée entre (0, 100) et (5/2, 0). Au point correspondant à x = 5/4, une ligne tangente est tracée, et cette droite est parallèle à la droite sécante. — Figure$\PageIndex{8}$ : Au temps$t=5/4$ sec, la vitesse de la roche est égale à sa vitesse moyenne entre le moment où elle tombe et le moment où elle touche le sol.

Exercice$\PageIndex{2}$

Supposons qu'une balle tombe d'une hauteur de 200 pieds. Sa position dans le temps$t$ est$s(t)=−16t^2+200.$ Trouvez le moment$t$ où la vitesse instantanée de la balle est égale à sa vitesse moyenne.

Allusion: Déterminez d'abord combien de temps il faut à la balle pour toucher le sol. Ensuite, déterminez la vitesse moyenne de la balle entre le moment où elle est lâchée et celui où elle touche le sol.

Réponse: $\frac{5}{2\sqrt{2}}$seconde

Corollaires du théorème de la valeur moyenne

Examinons maintenant trois corollaires du théorème de la valeur moyenne. Ces résultats ont des conséquences importantes, que nous utiliserons dans les prochaines sections.

À ce stade, nous savons que la dérivée de toute fonction constante est zéro. Le théorème de la valeur moyenne nous permet de conclure que l'inverse est également vrai. En particulier, si$f′(x)=0$ pour tous$x$ dans un certain intervalle$I$, alors$f(x)$ est constant sur cet intervalle. Ce résultat peut sembler intuitivement évident, mais il a des implications importantes qui ne le sont pas, et nous en discuterons prochainement.

Corollaire 1 : Fonctions dont la dérivée est nulle

$f$Soyons différenciables sur un intervalle$I$. Si$f′(x)=0$ pour tous$x∈I$, alors$f(x)=$ constant pour tous$x∈I.$

Une preuve

Puisque$f$ est différenciable$I$,$f$ doit être continu$I$. Supposons que ce n'$f(x)$est pas constant pour tous$x$$I$. Ensuite, il existe$a,b∈I$, où$a≠b$ et$f(a)≠f(b).$ choisissez la notation de sorte que,$a<b.$ par conséquent,

\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]

Comme$f$ il s'agit d'une fonction dérivable, selon le théorème de la valeur moyenne, il existe$c∈(a,b)$ une telle

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Il existe donc une$c∈I$ telle chose$f′(c)≠0$ qui contredit l'hypothèse selon laquelle$f′(x)=0$ pour tous$x∈I$.

□

De « Corollaire 1 : fonctions avec une dérivée de zéro », il s'ensuit que si deux fonctions ont la même dérivée, elles diffèrent au plus par une constante.

Corollaire 2 : Théorème de la différence constante

Si$f$ et$g$ sont différentiables sur un intervalle$I$ et$f′(x)=g′(x)$ pour tous$x∈I$, alors$f(x)=g(x)+C$ pour une certaine constante$C$.

Une preuve

Let$h(x)=f(x)−g(x).$ Then,$h′(x)=f′(x)−g′(x)=0$ pour tous$x∈I.$ Par corollaire 1, il existe une constante$C$ telle que$h(x)=C$ pour tous$x∈I$. Par conséquent,$f(x)=g(x)+C$ pour tous$x∈I.$

□

Le troisième corollaire du théorème de la valeur moyenne explique quand une fonction augmente et quand elle diminue. Rappelez-vous qu'une fonction$f$ augmente à$f(x_1)<f(x_2)$ chaque$I$ fois$x_1<x_2$, alors qu'elle$f$ diminue à$I$ chaque$f(x_1)>f(x_2)$ fois$x_1<x_2$. À l'aide du théorème de la valeur moyenne, nous pouvons montrer que si la dérivée d'une fonction est positive, alors la fonction augmente ; si la dérivée est négative, alors la fonction diminue (Figure$\PageIndex{9}$). Nous utilisons ce fait dans la section suivante, où nous montrons comment utiliser la dérivée d'une fonction pour localiser les valeurs maximales et minimales locales de la fonction et comment déterminer la forme du graphe.

Ce fait est important car cela signifie que pour une fonction donnée$f$, s'il existe une fonction$F$ telle que$F′(x)=f(x)$ ; alors, les seules autres fonctions dont la dérivée est égale$F(x)+C$ à$f$ concernent une constante$C$. Nous discuterons de ce résultat plus en détail plus loin dans le chapitre.

Une fonction f (x) vaguement sinusoïdale est représentée graphiquement. Il augmente à partir de quelque part dans le deuxième quadrant jusqu'à (a, f (a)). Dans cette section, il est noté que f' — Figure$\PageIndex{9}$ : Si une fonction possède une dérivée positive sur un certain intervalle$I$, alors la fonction augmente sur cet intervalle$I$ ; si la dérivée est négative sur un certain intervalle$I$, la fonction diminue sur cet intervalle$I$.

Corollaire 3 : Fonctions croissantes et décroissantes

$f$Soit continu sur l'intervalle fermé$[a,b]$ et différenciable sur l'intervalle ouvert$(a,b)$.

Si$f′(x)>0$ pour tout$x∈(a,b)$, alors une fonction croissante$f$ est terminée$[a,b].$
Si$f′(x)<0$ pour tout$x∈(a,b)$, alors$f$ une fonction décroissante est-elle terminée$[a,b].$

Une preuve

Nous allons le prouver ; la preuve de ii. est similaire. Suppose que$f$ ce n'est pas une fonction croissante activée$I$. Alors il existe$a$ et$b$ dans$I$ tel que$a<b$, mais$f(a)≥f(b)$. Comme$f$ il s'agit d'une fonction dérivable$I$, selon le théorème de la valeur moyenne, il existe une$c∈(a,b)$ telle fonction que

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Depuis$f(a)≥f(b)$, nous le savons$f(b)−f(a)≤0$. En outre, nous$a<b$ indique que$b−a>0.$ Nous concluons que

\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]

Cependant,$f′(x)>0$ pour tous$x∈I$. Il s'agit d'une contradiction et$f$ doit donc être une fonction de plus en plus terminée$I$.

□

Concepts clés

$f$Il est continu sur$[a,b]$ et dérivable sur$(a,b)$ et$f(a)=f(b)$, alors il existe un point$c∈(a,b)$ tel que$f′(c)=0.$ c'est le théorème de Rolle.
S'il$f$ est continu$[a,b]$ et dérivable$(a,b)$, alors il existe un point$c∈(a,b)$ tel que\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] c'est le théorème de la valeur moyenne.
S'il est$f'(x)=0$ supérieur à un intervalle$I$, alors$f$ est constant$I$.
Si deux fonctions dérivables$f$ et$f′(x)=g′(x)$ se$g$ satisfont$I$, alors$f(x)=g(x)+C$ pour une certaine constante$C$.
S'il est$f′(x)>0$ supérieur à un intervalle$I$, alors$f$ augmente de plus en plus$I$. Si la valeur$f$ est$f′(x)<0$ supérieure$I$, elle diminue à nouveau$I$.

Lexique

théorème de la valeur moyenne: s'$f$il est continu$[a,b]$ et différenciable$(a,b)$, alors il existe$c∈(a,b)$ tel que$f′(c)=\frac{f(b)−f(a)}{b−a}$

théorème de Rolle: si$f$ est continu$[a,b]$ et différentiable, et si$(a,b)$$f(a)=f(b)$, alors il existe une$c∈(a,b)$ telle situation que$f′(c)=0$