4.3E : Exercices pour la section 4.3

Last updated
Save as PDF

Page ID: 197633

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Dans le précalcul, vous avez appris une formule pour la position du maximum ou du minimum d'une équation quadratique$y=ax^2+bx+c$, qui était$m=−\frac{b}{2a}$. Prouvez cette formule en utilisant le calcul.

2) Si vous trouvez un minimum absolu sur un intervalle,$[a,b],$ pourquoi devez-vous vérifier les paramètres ? Dessinez un graphique qui soutient votre hypothèse.

Réponse: Sur un intervalle fermé, les paramètres se situent souvent au-dessus ou en dessous de tout extrême local (relatif). Les réponses peuvent varier pour le graphique.

3) Si vous examinez une fonction sur un intervalle$(a,b),$ pour$a$ et une valeur$b$ finie, est-il possible de ne pas avoir de maximum absolu ou de minimum absolu ?

4) Lorsque vous recherchez des points critiques pour localiser les extrêmes d'une fonction$f$, expliquez pourquoi vous devez également déterminer les points non définis.$f'(x)$ Dessinez un graphique à l'appui de votre explication.

Réponse: Les points du graphique indiquant l'$f$emplacement d'un angle, d'une cuspide, d'une discontinuité de saut ou d'une discontinuité amovible peuvent facilement constituer des extrêmes absolus (ou locaux) de la fonction. Les réponses peuvent varier pour le graphique.

5) Pouvez-vous avoir un maximum absolu limité pour$y=ax^2+bx+c$ plus de$(−∞,∞)$ ? Expliquez pourquoi ou pourquoi ne pas utiliser des arguments graphiques.

6) Pouvez-vous avoir un maximum absolu$y=ax^3+bx^2+cx+d$ fini pour une surestimation$(−∞,∞)$ en supposant que cette valeur$a$ est différente de zéro ? Expliquez pourquoi ou pourquoi ne pas utiliser des arguments graphiques.

Réponse: Non ; les réponses peuvent varier

7)$m$ Soit le nombre de minima locaux et$M$ le nombre de maxima locaux. Pouvez-vous créer une fonction où$M>m+2$ ? Dessinez un graphique à l'appui de votre explication.

8) Est-il possible d'avoir plus d'un maximum absolu ? Utilisez un argument graphique pour prouver votre hypothèse.

Réponse: Puisque le maximum absolu est la valeur de la fonction (sortie) plutôt que la valeur x, la réponse est non ; les réponses peuvent varier

9) Est-il possible de ne pas avoir de minimum ou de maximum absolu pour une fonction ? Si c'est le cas, créez une telle fonction. Dans le cas contraire, expliquez pourquoi cela n'est pas possible.

10) [T] Tracez la fonction$y=e^{ax}.$ Pour quelles valeurs de$a$, sur n'importe quel domaine infini, aurez-vous un minimum absolu et un maximum absolu ?

Réponse: Quand$a=0$

Dans les exercices 11 à 14, déterminez où se situent les maxima et minima locaux et absolus sur le graphique donné. Supposons que les domaines sont des intervalles fermés, sauf indication contraire.

11)

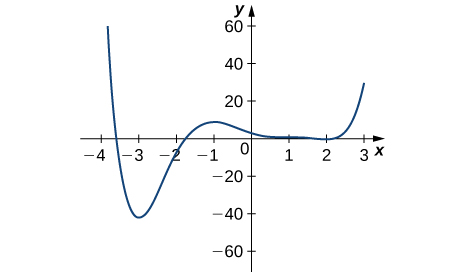
$La fonction représentée graphiquement commence à (−4, 60), diminue rapidement jusqu'à (−3, −40), augmente jusqu'à (−1, 10) avant de diminuer lentement jusqu'à (2, 0), puis augmente rapidement jusqu'à (3, 30).$

(12)

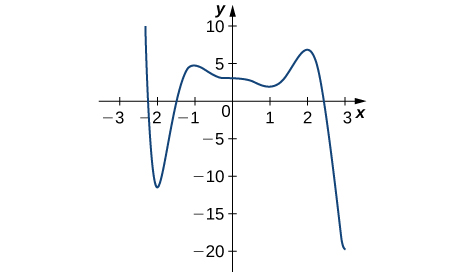
$La fonction représentée graphiquement commence à (−2,2, 10), diminue rapidement jusqu'à (−2, −11), augmente jusqu'à (−1, 5) avant de diminuer lentement jusqu'à (1, 3), puis augmente jusqu'à (2, 7), puis diminue jusqu'à (3, −20).$

Réponse: Minimum absolu à 3 ; maximum absolu à −2,2 ; minima locaux à −2, 1 ; maxima locaux à −1, 2

13)

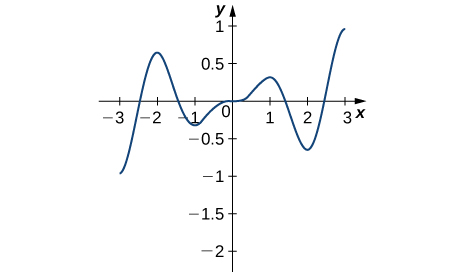
$La fonction représentée graphiquement commence à (−3, −1), augmente rapidement jusqu'à (−2, 0,7), diminue jusqu'à (−1, −0,25) avant de diminuer lentement jusqu'à (1, 0,25), puis diminue jusqu'à (2, 0,7), puis augmente jusqu'à (3, 1).$

(14)

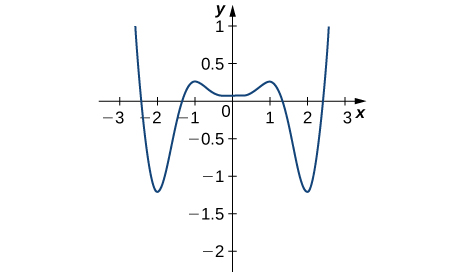
$La fonction représentée graphiquement commence à (−2,5, 1), diminue rapidement jusqu'à (−2, −1,25), augmente jusqu'à (−1, 0,25) avant de diminuer lentement jusqu'à (0, 0,2), puis augmente lentement jusqu'à (1, 0,25), puis diminue rapidement jusqu'à (2, −1,25) et augmente enfin jusqu'à (2,5, 1).$

Réponse: Minimums absolus à −2, 2 ; maxima absolus à −2,5, 2,5 ; minimum local à 0 ; maxima locaux à −1, 1

Pour les exercices 15 à 18, tracez des$f(x)$ graphiques continus sur l'intervalle$[−4,4]$ avec les propriétés suivantes :

15) Maximum absolu à$x=2$ et minima absolus à$x=±3$

16) Minimum absolu à$x=1$ et maximum absolu à$x=2$

Réponse: Les réponses peuvent varier.

17) Maximum$x=4,$ absolu au minimum absolu au maximum$x=−1,$ local à$x=−2,$ et point critique qui n'est ni un maximum ni un minimum à$x=2$

18) Maxima absolus à$x=2$ et$x=−3$, minimum local à$x=1$ et minimum absolu à$x=4$

Réponse: Les réponses peuvent varier.

Dans les exercices 19 à 28, trouvez les points critiques dans les domaines des fonctions données.

19)$y=4x^3−3x$

(20)$y=4\sqrt{x}−x^2$

Réponse: $x=1$

(21)$y=\dfrac{1}{x−1}$

(22)$y=\ln(x−2)$

Réponse: Aucune

23)$y=\tan(x)$

(24)$y=\sqrt{4−x^2}$

Réponse: $x=0$

25)$y=x^{3/2}−3x^{5/2}$

(26)$y=\dfrac{x^2−1}{x^2+2x−3}$

Réponse: Aucune

(27)$y=\sin^2(x)$

(28)$y=x+\dfrac{1}{x}$

Réponse: $x=−1$et$x = 1$

Dans les exercices 29 à 39, trouvez les maxima locaux et/ou absolus pour les fonctions dans le domaine spécifié.

29)$f(x)=x^2+3$ plus$[−1,4]$

30)$y=x^2+\dfrac{2}{x}$ plus$[1,4]$

Réponse: Maximum absolu :$x=4, y=\frac{33}{2}$ ; minimum absolu :$x=1, y=3$

31)$y=(x−x^2)^2$ plus$[−1,1]$

32)$y=\dfrac{1}{x−x^2}$ plus$[0,1]$

Réponse: Minimum absolu :$x=\frac{1}{2}, y=4$

33)$y=\sqrt{9−x}$ plus$[1,9]$

34)$y=x+\sin(x)$ plus$[0,2π]$

Réponse: Maximum$x=2π, y=2π;$ absolu : minimum absolu :$x=0, y=0$

35)$y=\dfrac{x}{1+x}$ plus$[0,100]$

36)$y=|x+1|+|x−1|$ plus$[−3,2]$

Réponse: Maximum$x=−3, y = 6;$ absolu : minimum absolu :$−1≤x≤1, y=2$

37)$y=\sqrt{x}−\sqrt{x^3}$ plus$[0,4]$

38)$y=\sin x+\cos x$ plus$[0,2π]$

Réponse: Maximum absolu :$x=\frac{π}{4}, y=\sqrt{2}$ ; minimum absolu :$x=\frac{5π}{4}, y=−\sqrt{2}$

39)$y=4\sin θ−3\cos θ$ plus$[0,2π]$

Dans les exercices 40 à 45, déterminez les minima et maxima locaux et absolus pour les fonctions terminées$(−∞,∞).$

40)$y=x^2+4x+5$

Réponse: Minimum absolu :$x=−2, y=1$

41)$y=x^3−12x$

(42)$y=3x^4+8x^3−18x^2$

Réponse: Minimum absolu : maximum$x=−3, y=−135;$ local :$x=0, y=0$ ; minimum local :$x=1, y=−7$

43)$y=x^3(1−x)^6$

44)$y=\dfrac{x^2+x+6}{x−1}$

Réponse: Maximum local :$x=1−2\sqrt{2}, y=3−4\sqrt{2}$ ; minimum local :$x=1+2\sqrt{2}, y=3+4\sqrt{2}$

45)$y=\dfrac{x^2−1}{x−1}$

Dans les exercices 46 à 50, utilisez une calculatrice pour représenter graphiquement la fonction et estimer les maxima et minima absolus et locaux. Ensuite, résolvez-les de manière explicite.

46) [T]$y=3x\sqrt{1−x^2}$

Réponse: Maximum$x=\frac{\sqrt{2}}{2}, y=\frac{3}{2};$ absolu : minimum absolu :$x=−\frac{\sqrt{2}}{2}, y=−\frac{3}{2}$

47) [T]$y=x+\sin(x)$

48) [T]$y=12x^5+45x^4+20x^3−90x^2−120x+3$

Réponse: Maximum local :$x=−2,y=59$ ; minimum local :$x=1, y=−130$

49) [T]$y=\dfrac{x^3+6x^2−x−30}{x−2}$

50) [T]$y=\dfrac{\sqrt{4−x^2}}{\sqrt{4+x^2}}$

Réponse: Maximum$x=0, y=1;$ absolu : minimum absolu :$x=−2,2, y=0$

51) Une entreprise qui produit des téléphones portables a une fonction de coût qui$C=x^2−1200x+36,400,$ indique où se$C$ situe le coût en dollars et$x$ le nombre de téléphones portables produits (en milliers). Combien d'unités de téléphone portable (en milliers) minimisent cette fonction de coût ?

52) Une balle est lancée en l'air et sa position est donnée par$h(t)=−4.9t^2+60t+5m.$ Trouver la hauteur à laquelle la balle arrête de monter. Combien de temps après son lancement, cela se produit-il ?

Réponse: $h=\frac{9245}{49}$m,$t=\frac{300}{49}$ s

Pour les exercices 53 à 54, considérez la production d'or pendant la ruée vers l'or en Californie (1848—1888). La production d'or peut être modélisée en fonction$G(t)=\dfrac{(25t)}{(t^2+16)}$ du nombre d'$t$années écoulées depuis le début de la$G$ ruée$(0≤t≤40)$ et du nombre d'onces d'or produites (en millions). Un résumé des données est présenté dans la figure suivante.

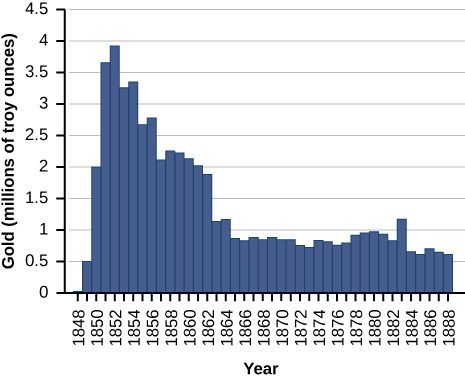
$Le graphique à barres montre l'or (en millions d'onces troy) par an, de 1848 à 1888. En 1848, le graphique à barres indique 0,05 ; en 1849, 0,5 ; en 1850, 2 ; en 1851, 3,6 ; en 1852, 3,9 ; en 1853, 3,3 ; en 1854, 3,4 ; en 1855, 2,6 ; en 1856, 2,75 ; en 1857, 2,1 ; en 1857, 2,1 ; en 1858, 2,2 ; en 1859, 2,15 ; en 1860, 2,1 ; en 1861, 2 ; en 1862, 1,8 ; en 1863, 1,1 ; en 1864, 1,15 ; en 1860, 2,1 ; en 1861, 2 ; en 1862, 1,8 ; en 1863, 1,1 ; en 1864, 1,15 15 ; en 1865, 0,9 ; en 1866, 0,85 ; en 1867, 0,9 ; en 1868, 0,85 ; en 1869, 0,9 ; en 1870, 0,85 ; en 1871, 0,85 ; en 1872, 0,75 ; en 1873, 0,7 ; en 1874, 0,8 ; en 1875, 0,75 ; en 1876, 0,7 ; en 1877, 0,73 ; en 1878, 0,9 ; en 1879, 0,95 ; en 1880, 1 ; en 1881, 0,95 ; en 1882, 0,85 ; en 1883, 1,1 ; en 1884, 0,6 ; en 1885, 1 0,55 ; en 1886, 0,65 ; en 1887, 0,6 ; et en 1888, 0,55.$

53) Déterminez quand la production d'or maximale (locale et mondiale) s'est produite et la quantité d'or produite pendant cette période maximale.

54) Déterminez à quel moment la production minimale d'or (locale et mondiale) s'est produite. Quelle a été la quantité d'or produite pendant ce minimum ?

Réponse: Le minimum mondial était en 1848, alors qu'aucun or n'était produit.

Dans les exercices 55 et 56, déterminez les points critiques, les maxima et les minima pour les fonctions par morceaux données.

55)$y= \begin{cases} x^2−4x, & \text{if }0≤x≤1\\x^2−4, & \text{if }1<x≤2 \end{cases}$

56)$y=\begin{cases}x^2+1, & \text{if }x≤1 \\ x^2−4x+5, & \text{if }x>1\end{cases}$

Réponse: Minimaux absolus :$x=0, x=2, y=1$ maximum local à$x=1, y=2$

Dans les exercices 57 à 58, trouvez les points critiques des fonctions génériques suivantes. Sont-ils des maxima, des minima ou aucun des deux ? Indiquez les conditions nécessaires.

57)$y=ax^2+bx+c,$ étant donné que$a>0$

58)$y=(x−1)^a$, étant donné que$a>1$

Réponse: Pas de maxima/minima si$a$ c'est impair, minimum$x=1$ si$a$ c'est pair

Contributeurs et attributions

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added answers for exercises 2 and 4.