4.3 : Maxima et minima

Last updated
Save as PDF

Page ID: 197619

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Définissez les extrêmes absolus.
Définissez les extrêmes locaux.
Expliquez comment déterminer les points critiques d'une fonction sur un intervalle fermé.
Décrire comment utiliser les points critiques pour localiser les extrêmes absolus sur un intervalle fermé.

Étant donné une fonction particulière, nous cherchons souvent à déterminer les valeurs les plus grandes et les plus petites de la fonction. Ces informations sont importantes pour créer des graphiques précis. Trouver les valeurs maximale et minimale d'une fonction a également une importance pratique, car nous pouvons utiliser cette méthode pour résoudre des problèmes d'optimisation, tels que la maximisation des profits, la minimisation de la quantité de matériau utilisée dans la fabrication d'une boîte en aluminium ou la détermination de la hauteur maximale qu'une fusée peut atteindre. Dans cette section, nous allons voir comment utiliser les dérivées pour déterminer les valeurs les plus grandes et les plus petites d'une fonction.

Extrema absolu

Considérez la fonction\(f(x)=x^2+1\) sur l'intervalle\((−∞,∞)\). Comme\(x→±∞, f(x)→∞\). Par conséquent, la fonction n'a pas de plus grande valeur. Cependant, puisque\(x^2+1≥1\) pour tous les nombres réels\(x\) et\(x^2+1=1\) quand\(x=0\), la fonction a la plus petite valeur\(1\), quand\(x=0\). Nous disons que\(1\) c'est le minimum absolu\(f(x)=x^2+1\) et que cela se produit à\(x=0\). Nous disons que\(f(x)=x^2+1\) cela n'a pas de maximum absolu (Figure\(\PageIndex{1}\)).

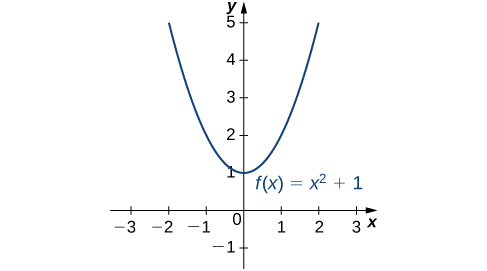
La fonction f (x) = x^2 + 1 est représentée graphiquement, et son minimum de 1 est considéré comme étant à x = 0. — Figure\(\PageIndex{1}\) : La fonction donnée a un minimum absolu de\(1\) at\(x=0\). La fonction n'a pas de maximum absolu.

Définition : Absolute Extrema

\(f\)Soit une fonction définie sur un intervalle\(I\) et laissez\(c∈I\). Nous disons qu'\(f\)il a un maximum absolu\(I\) sur «\(c\) if\(f(c)≥f(x)\) for all »\(x∈I\). Nous disons qu'\(f\)il y a un minimum absolu\(I\) sur «\(c\) if\(f(c)≤f(x)\) for all »\(x∈I\). S'il\(f\) a un maximum absolu sur\(I\) at\(c\) ou un minimum absolu sur\(I\) at\(c\), nous disons qu'\(f\)il a un extremum absolu sur\(I\) at\(c\).

Avant de poursuivre, notons deux points importants concernant cette définition. Tout d'abord, le terme absolu ici ne fait pas référence à la valeur absolue. Un extremum absolu peut être positif, négatif ou nul. Deuxièmement, si une fonction\(f\) possède un extremum absolu sur un intervalle\(I\) at\(c\), l'extremum absolu est\(f(c)\). Le nombre réel\(c\) est un point du domaine où se trouve l'extremum absolu. Par exemple, considérez la fonction\(f(x)=1/(x^2+1)\) sur l'intervalle\((−∞,∞)\). Depuis

\[f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber \]

pour tous les nombres réels\(x\), nous disons qu'\(f\)il a un maximum absolu supérieur\((−∞,∞)\) à\(x=0\). Le maximum absolu est de\(f(0)=1\). Il se produit à\(x=0\), comme le montre la figure\(\PageIndex{2}\) (b).

Une fonction peut avoir à la fois un maximum absolu et un minimum absolu, un seul extremum, ou aucun des deux. La figure\(\PageIndex{2}\) montre plusieurs fonctions et certaines des différentes possibilités concernant les extrêmes absolus. Cependant, le théorème suivant, appelé théorème des valeurs extrêmes, garantit qu'une fonction continue\(f\) sur un intervalle fermé et borné\([a,b]\) possède à la fois un maximum absolu et un minimum absolu.

Cette figure comporte six parties a, b, c, d, e et f. Sur la figure a, la ligne f (x) = x^3 est représentée, et il est noté qu'elle n'a ni minimum ni maximum absolu. Sur la figure b, la droite f (x) = 1/ (x^2 + 1) est représentée, qui est proche de 0 sur la majeure partie de sa longueur et monte jusqu'à une bosse à (0, 1) ; elle n'a pas de minimum absolu, mais elle a un maximum absolu de 1 à x = 0. Dans la figure c, la ligne f (x) = cos x est représentée, avec des minimums absolus de −1 à ±π, ± 3π,... et des maximums absolus de 1 à 0, ±2π, ±4π,... Dans la figure d, la fonction fragmentaire f (x) = 2 — x^2 pour 0 ≤ x < 2 et x — 3 pour 2 ≤ x ≤ 4 est illustrée, avec un maximum absolu de 2 à x = 0 et aucun minimum absolu. Dans la figure e, la fonction f (x) = (x — 2) 2 est illustrée sur [1, 4], qui a un maximum absolu de 4 à x = 4 et un minimum absolu de 0 à x = 2. Dans la figure f, la fonction f (x) = x/ (2 − x) est représentée sur [0, 2), avec un minimum absolu de 0 à x = 0 et aucun maximum absolu. — Figure\(\PageIndex{2}\) : Les graphes (a), (b) et (c) montrent plusieurs possibilités d'extrêmes absolus pour les fonctions ayant un domaine de\((−∞,∞).\) graphes (d), (e) et (f) montrent plusieurs possibilités d'extrêmes absolus pour les fonctions dont le domaine est un intervalle borné.

Théorème\(\PageIndex{1}\): Extreme Value Theorem

S'il s'\(f\)agit d'une fonction continue sur l'intervalle fermé et borné\([a,b]\), alors il y\(f\) a un point où le maximum absolu est dépassé\([a,b]\) et il y a un point où il y\(f\) a un minimum absolu au-dessus\([a,b]\).\([a,b]\)\([a,b]\)

La preuve du théorème des valeurs extrêmes dépasse le cadre de ce texte. En général, cela est prouvé dans un cours sur l'analyse réelle. Il y a quelques points clés à noter à propos de l'énoncé de ce théorème. Pour que le théorème des valeurs extrêmes s'applique, la fonction doit être continue sur un intervalle fermé et borné. Si l'intervalle\(I\) est ouvert ou si la fonction présente ne serait-ce qu'un seul point de discontinuité, la fonction peut ne pas avoir de maximum ou de minimum absolu\(I\). Par exemple, considérez les fonctions illustrées dans les figures\(\PageIndex{2}\) (d), (e) et (f). Ces trois fonctions sont définies sur des intervalles bornés. Cependant, la fonction du graphe (e) est la seule qui possède à la fois un maximum absolu et un minimum absolu sur son domaine. Le théorème des valeurs extrêmes ne peut pas être appliqué aux fonctions des graphes (d) et (f) car aucune de ces fonctions n'est continue sur un intervalle fermé et borné. Bien que la fonction du graphe (d) soit définie sur l'intervalle fermé\([0,4]\), elle est discontinue à\(x=2\). La fonction possède un maximum absolu\([0,4]\) mais n'a pas de minimum absolu. La fonction du graphe (f) est continue sur l'intervalle semi-ouvert\([0,2)\), mais n'est pas définie à\(x=2\) et n'est donc pas continue sur un intervalle fermé et borné. La fonction possède un maximum absolu\([0,2)\), mais pas un maximum absolu\([0,2)\). Ces deux graphiques illustrent pourquoi une fonction sur un intervalle borné peut ne pas avoir de maximum absolu et/ou de minimum absolu.

Avant de voir comment déterminer les extrêmes absolus, examinons le concept connexe d'extrema local. Cette idée est utile pour déterminer où se situent les extrêmes absolus.

Points critiques et extrêmes locaux

Considérez la fonction\(f\) illustrée dans la figure\(\PageIndex{3}\). Le graphique peut être décrit comme deux montagnes avec une vallée au milieu. La valeur maximale absolue de la fonction se produit au pic le plus élevé, à\(x=2\). Cependant,\(x=0\) c'est aussi un point d'intérêt. Bien que\(f(0)\) ce ne soit pas la plus grande valeur de\(f\), la valeur\(f(0)\) est supérieure à celle de toutes\(f(x)\) les valeurs\(x\) proches de 0. Nous disons qu'\(f\)il a un maximum local à\(x=0\). De même, la fonction\(f\) n'a pas de minimum absolu, mais elle a un minimum local\(x=1\) car il\(f(1)\) est inférieur à celui\(f(x)\) d'\(x\)environ 1.

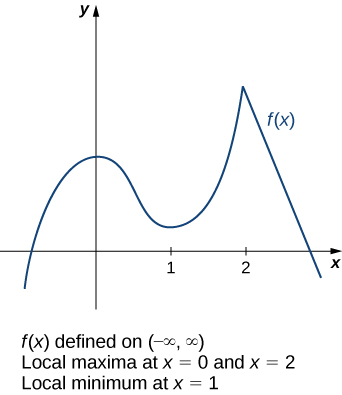
La fonction f (x) est représentée, qui se courbe vers le haut à partir du quadrant III, ralentit dans le quadrant II, atteint un maximum local sur l'axe y, diminue pour atteindre un minimum local dans le quadrant I à x = 1, augmente jusqu'à un maximum local à x = 2 qui est supérieur à l'autre maximum local, puis diminue rapidement quadrant IV. — Figure\(\PageIndex{3}\) : Cette fonction\(f\) possède deux maxima locaux et un minimum local. Le maximum local à\(x=2\) est également le maximum absolu.

Définition : Local Extrema

Une fonction\(f\) a un maximum local à\(c\) s'il existe un intervalle ouvert\(I\) contenant un\(c\) tel intervalle qui\(I\) est contenu dans le domaine de\(f\) et\(f(c)≥f(x)\) pour tous\(x∈I\). Une fonction\(f\) a un minimum local\(c\) s'il existe un intervalle ouvert\(I\) contenant un\(c\) tel intervalle qui\(I\) est contenu dans le domaine de\(f\) et\(f(c)≤f(x)\) pour tous\(x∈I\). Une fonction\(f\) a un extremum local à\(c\) si\(f\) elle a un maximum local à\(c\) ou\(f\) un minimum local à\(c\).

Notez que s'il\(f\) a un extremum absolu à\(c\) et qu'\(f\)il est défini sur un intervalle contenant\(c\), il\(f(c)\) est également considéré comme un extremum local. Si un extremum absolu pour une fonction\(f\) se produit à un point final, nous ne le considérons pas comme un extremum local, mais nous l'appelons un extremum de point final.

À partir du graphe d'une fonction\(f\), il est parfois facile de voir où se situe un maximum ou un minimum local. Cependant, cela n'est pas toujours facile à voir, car les caractéristiques intéressantes du graphique d'une fonction peuvent ne pas être visibles car elles apparaissent à très petite échelle. De plus, il se peut que nous n'ayons pas de graphique de la fonction. Dans ces cas, comment pouvons-nous utiliser une formule pour une fonction afin de déterminer où se produisent ces extrêmes ?

Pour répondre à cette question, examinons à\(\PageIndex{3}\) nouveau la figure. Les extrêmes locaux se produisent à\(x=0, x=1,\) et\(x=2.\) remarquez qu'à\(x=0\) et\(x=1\), la dérivée\(f'(x)=0\). À\(x=2\), la dérivée\(f'(x)\) n'existe pas, car la fonction y\(f\) a un angle. En fait, si\(f\) elle possède un extremum local en un point\(x=c\), la dérivée\(f'(c)\) doit satisfaire à l'une des conditions suivantes :\(f'(c)=0\) soit elle n'\(f'(c)\)est pas définie. Une telle valeur\(c\) est connue comme un point critique et elle est importante pour trouver des valeurs extrêmes pour les fonctions.

Définition : points critiques

\(c\)Soyons un point intérieur dans le domaine de\(f\). Nous disons que\(c\) c'est un point critique pour savoir\(f\) si\(f'(c)=0\) ou n'\(f'(c)\)est pas défini.

Comme mentionné précédemment, s'il y\(f\) a un extremum local en un point\(x=c\), alors\(c\) il doit s'agir d'un point critique de\(f\). Ce fait est connu sous le nom de théorème de Fermat.

Théorème\(\PageIndex{2}\): Fermat’s Theorem

S'il\(f\) a un extremum local à\(c\) et\(f\) est différenciable à\(c\), alors\(f'(c)=0.\)

Une preuve

Supposons qu'\(f\)il possède un extremum local à\(c\) et\(f\) qu'il est différenciable à\(c\). Nous devons le montrer\(f'(c)=0\). Pour ce faire, nous allons montrer que\(f'(c)≥0\) et\(f'(c)≤0\) donc\(f'(c)=0\). Puisque\(f\) a un extremum local à\(c\),\(f\) a un maximum local ou un minimum local à\(c\). Supposons\(f\) que le maximum local soit égal à\(c\). Le cas dans lequel\(f\) a un minimum local à\(c\) peut être traité de la même manière. Il existe alors un intervalle ouvert I tel que\(f(c)≥f(x)\) pour tous\(x∈I\). Comme\(f\) il est différenciable à\(c\) partir de la définition de la dérivée, nous savons que

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Puisque cette limite existe, les deux limites unilatérales existent également et sont égales\(f'(c)\). Par conséquent,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2} \]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Comme\(f(c)\) c'est un maximum local, on le voit\(f(x)−f(c)≤0\) de\(x\) près\(c\). Donc, pour\(x\) presque\(c\), mais\(x>c\), nous l'avons fait\(\frac{f(x)−f(c)}{x−c}≤0\). À partir de l'équation \ ref {FerMateQn2}, nous concluons que\(f'(c)≤0\). De même, il peut être démontré que,\(f'(c)≥0.\) par conséquent,\(f'(c)=0.\)

□

À partir du théorème de Fermat, nous concluons que s'il\(f\) a un extremum local à\(c\), alors l'un\(f'(c)=0\) ou l'autre n'\(f'(c)\)est pas défini. En d'autres termes, les extrêmes locaux ne peuvent se produire qu'aux points critiques.

Notez que ce théorème ne prétend pas qu'une fonction\(f\) doit avoir un extremum local à un point critique. Il indique plutôt que les points critiques peuvent être considérés comme des extrêmes locaux. Par exemple, considérez la fonction\(f(x)=x^3\). Nous avons\(f'(x)=3x^2=0\) quand\(x=0\). C'\(x=0\)est donc un point critique. Cependant,\(f(x)=x^3\) il augmente\((−∞,∞)\) et n'\(f\)a donc pas d'extremum local à\(x=0\). Dans la figure\(\PageIndex{4}\), nous voyons plusieurs possibilités différentes pour les points critiques. Dans certains de ces cas, les fonctions présentent des extrêmes locaux aux points critiques, alors que dans d'autres cas, elles n'en ont pas. Notez que ces graphiques ne montrent pas toutes les possibilités de comportement d'une fonction à un point critique.

Cette figure comporte cinq parties a, b, c, d et e. Sur la figure a, une parabole est représentée face vers le bas dans le quadrant I ; il y a une tangente horizontale au maximum local marqué f' (c) = 0. Dans la figure b, il y a une fonction dessinée avec une asymptote en c, ce qui signifie que la fonction augmente vers l'infini des deux côtés de c ; il est noté que f' (c) n'est pas défini. La figure c montre une version du graphique des valeurs absolues qui a été décalée de telle sorte que son minimum se trouve dans le quadrant I avec x = c. Il est noté que f' (c) n'est pas défini. La figure d montre une version de la fonction f (x) = x^3 qui a été déplacée de telle sorte que son point d'inflexion se trouve dans le quadrant I avec x = c. Son point d'inflexion à (c, f (c)) est traversé par une ligne horizontale, et il est noté que f' (c) = 0. La figure e montre une version de la fonction f (x) = x1/3 qui a été déplacée de telle sorte que son point d'inflexion se trouve dans le quadrant I avec x = c. Son point d'inflexion à (c, f (c)) est traversé par une ligne verticale, et il est noté que f' (c) n'est pas défini. — Figure\(\PageIndex{4}\) : (a—e) Une fonction\(f\) a un point critique si elle n'est pas définie\(f'(c)=0\) ou\(c\) si elle n'\(f'(c)\)est pas définie. Une fonction peut avoir ou non un extremum local à un point critique.

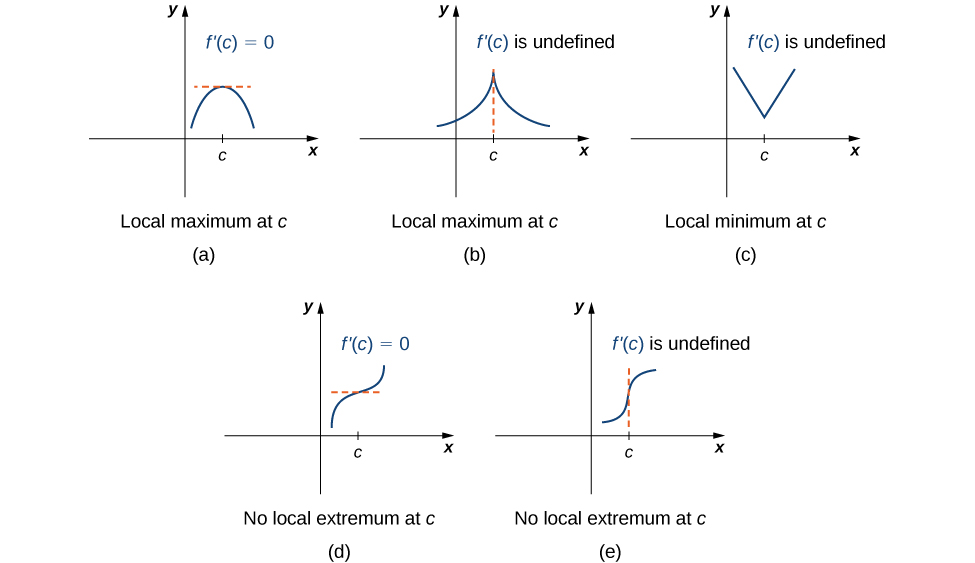
Plus loin dans ce chapitre, nous examinerons les méthodes analytiques permettant de déterminer si une fonction possède réellement un extremum local à un point critique. Pour l'instant, concentrons-nous sur la recherche de points critiques. Nous utiliserons des observations graphiques pour déterminer si un point critique est associé à un extremum local.

Exemple\(\PageIndex{1}\): Locating Critical Points

Pour chacune des fonctions suivantes, trouvez tous les points critiques. Utilisez un utilitaire de création graphique pour déterminer si la fonction possède un extremum local à chacun des points critiques.

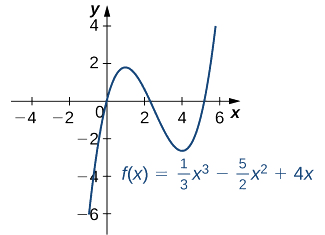
\(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
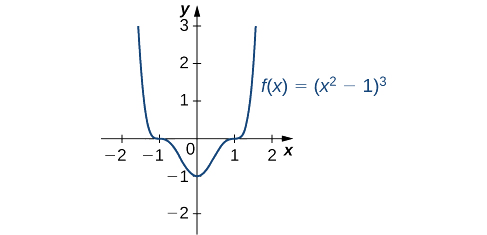
\(f(x)=(x^2−1)^3\)
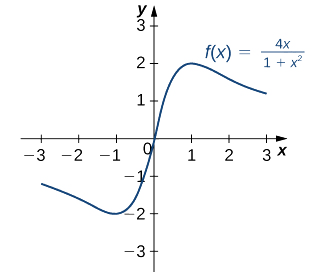
\(f(x)=\frac{4x}{1+x^2}\)

Solution

a. La dérivée\(f'(x)=x^2−5x+4\) est définie pour tous les nombres réels\(x\). Par conséquent, il suffit de trouver les valeurs pour\(x\) où\(f'(x)=0\). Puisque\(f'(x)=x^2−5x+4=(x−4)(x−1)\), les points critiques sont\(x=1\) et\(x=4.\) À partir du graphique de\(f\) la figure\(\PageIndex{5}\), nous voyons qu'il y\(f\) a un maximum local à\(x=1\) et un minimum local à\(x=4\).

La fonction f (x) = (1/3) x^3 — (5/2) x^2 + 4x est représentée graphiquement. La fonction a un maximum local à x = 1 et un minimum local à x = 4. — Figure\(\PageIndex{5}\) : Cette fonction possède un maximum local et un minimum local.

b. En utilisant la règle de la chaîne, nous voyons que la dérivée est

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

Par conséquent,\(f\) a des points critiques quand\(x=0\) et quand\(x^2−1=0\). Nous concluons que les points critiques sont\(x=0,±1\). Sur le graphique de\(f\) la Figure\(\PageIndex{6}\), nous voyons qu'il\(f\) a un minimum local (et absolu) à\(x=0\), mais qu'il n'a pas d'extremum local à\(x=1\) ou\(x=−1\).

La fonction f (x) = (x^2 − 1) 3 est représentée graphiquement. La fonction a un minimum local à x = 0 et des points d'inflexion à x = ±1. — Figure\(\PageIndex{6}\) : Cette fonction comporte trois points critiques :\(x=0\),\(x=1\), et\(x=−1\). La fonction a un minimum local (et absolu) à\(x=0\), mais n'a pas d'extrema aux deux autres points critiques.

c. Selon la règle du quotient, nous voyons que la dérivée est

\(f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

La dérivée est définie partout. Par conséquent, il suffit de trouver des valeurs pour\(x\) où\(f'(x)=0\). Résoudre\(f'(x)=0\), nous voyons ce\(4−4x^2=0,\) que cela implique\(x=±1\). Par conséquent, les points critiques sont\(x=±1\). Sur le graphique de\(f\) la figure\(\PageIndex{7}\), nous voyons que f a un maximum absolu à\(x=1\) et un minimum absolu à.\(x=−1.\) Par conséquent,\(f\) a un maximum local à\(x=1\) et un minimum local à\(x=−1\). (Notez que s'il\(f\) possède un extremum absolu sur un intervalle\(I\) à un point\(c\) qui n'est pas un point final de\(I\), alors\(f\) a un extremum local à\(c.)\)

La fonction f (x) = 4x/ (1 + x^2) est représentée graphiquement. La fonction a un maximum local/absolu à x = 1 et un minimum local/absolu à x = −1. — Figure\(\PageIndex{7}\) : Cette fonction possède un maximum absolu et un minimum absolu.

Exercice\(\PageIndex{1}\)

Trouvez tous les points critiques pour\(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Allusion: Calculer\(f'(x).\)

Réponse: \(x=\frac{−2}{3}, x=1\)

Trouver Absolute Extrema

Le théorème des valeurs extrêmes indique qu'une fonction continue sur un intervalle fermé et borné a un maximum absolu et un minimum absolu. Comme le montre la figure\(\PageIndex{2}\), l'un de ces extrêmes absolus ou les deux peuvent se produire à un point final. Toutefois, si aucun extremum absolu ne se produit à une extrémité, il doit apparaître à un point intérieur, auquel cas l'extremum absolu est un extremum local. Par conséquent, selon le théorème de Fermat, le point\(c\) où se produit l'extremum local doit être un point critique. Nous résumons ce résultat dans le théorème suivant.

Théorème\(\PageIndex{3}\): Location of Absolute Extrema

\(f\)Soit une fonction continue sur un intervalle fermé et limité\(I\). Le maximum absolu de\(f\) dépassement\(I\) et le minimum absolu de\(f\) dépassement\(I\) doivent se produire aux extrémités\(I\) ou aux points critiques de\(f\) l'entrée\(I\).

Avec cette idée en tête, examinons une procédure permettant de localiser les extrêmes absolus.

Stratégie de résolution de problèmes : localiser les extrêmes absolus sur un intervalle fermé

Considérez une fonction continue\(f\) définie sur l'intervalle fermé\([a,b].\)

Évaluez\(f\) aux points de terminaison\(x=a\) et\(x=b.\)
Trouvez tous les points critiques de\(f\) cet intervalle\((a,b)\) et évaluez-les en\(f\) fonction de ces points critiques.
Comparez toutes les valeurs trouvées dans (1) et (2). À partir de « Localisation des extrêmes absolus », les extrêmes absolus doivent se produire aux extrémités ou aux points critiques. Par conséquent, la plus grande de ces valeurs est le maximum absolu de\(f\). La plus petite de ces valeurs est le minimum absolu de\(f\).

Voyons maintenant comment utiliser cette stratégie pour déterminer les valeurs maximales et minimales absolues pour les fonctions continues.

Exemple\(\PageIndex{2}\): Locating Absolute Extrema

Pour chacune des fonctions suivantes, déterminez le maximum absolu et le minimum absolu sur l'intervalle spécifié et indiquez où ces valeurs se situent.

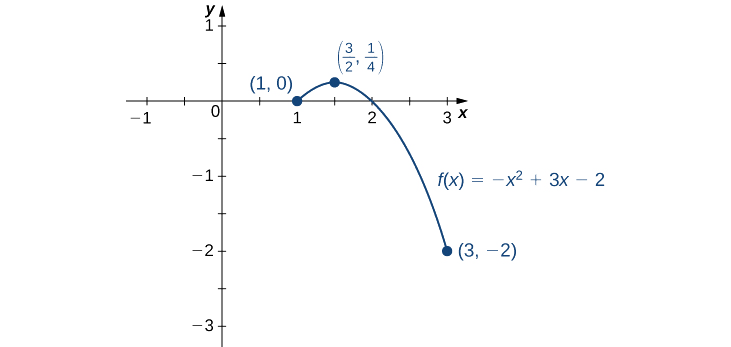
\(f(x)=−x^2+3x−2\)terminé\([1,3].\)
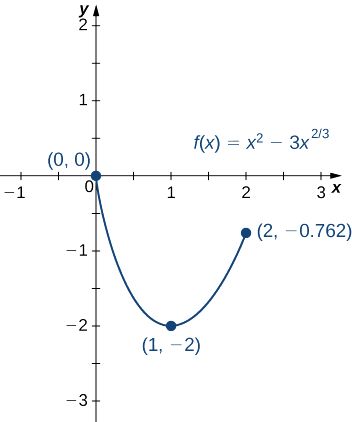
\(f(x)=x^2−3x^{2/3}\)terminé\([0,2]\).

Solution

a. Étape 1. Évaluez\(f\) aux points de terminaison\(x=1\) et\(x=3\).

\(f(1)=0\)et\(f(3)=−2\)

Étape 2. Puisque\(f'(x)=−2x+3, f'\) est défini pour tous les nombres réels Il n'y a\(x.\) donc aucun point critique où la dérivée n'est pas définie. Reste à savoir où\(f'(x)=0\). Puisque\(f'(x)=−2x+3=0 \) at\(x=\frac{3}{2}\) et\(\frac{3}{2}\) est dans l'intervalle\([1,3], f(\frac{3}{2})\) est candidat à un extremum absolu de\(f\) plus\([1,3]\). Nous évaluons\(f(\frac{3}{2})\) et trouvons

\(f\left(\frac{3}{2}\right)=\frac{1}{4}\).

Étape 3. Nous avons créé le tableau suivant pour comparer les valeurs trouvées aux étapes 1 et 2.

\(x\)	\(f(x)\)	Conclusion
\(1\)	\(0\)
\(\frac{3}{2}\)	\(\frac{1}{4}\)	Maximum absolu
\(3\)	\(−2\)	Minimum absolu

À partir du tableau, nous trouvons que le maximum absolu de\(f\) sur l'intervalle [1, 3] est\(\frac{1}{4}\) et qu'il se produit à\(x=\frac{3}{2}\). Le minimum absolu de l'\(f\)intervalle\([1, 3]\) est\(−2\), et il se produit\(x=3\) comme indiqué sur la figure\(\PageIndex{8}\).

La fonction f (x) = — x^2 + 3x — 2 est représentée graphiquement de (1, 0) à (3, −2), son maximum étant marqué à (3/2, 1/4). — Figure\(\PageIndex{8}\) : Cette fonction possède à la fois un maximum absolu et un minimum absolu.

b. Étape 1. Évaluez\(f\) aux points de terminaison\(x=0\) et\(x=2\).

\(f(0)=0\)et\(f(2)=4−3\left(2\right)^{2/3}≈−0.762\)

Étape 2. La dérivée de\(f\) est donnée par

\(f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}\)

pour\(x≠0\). La dérivée est nulle quand\(2x^{4/3}−2=0\), ce qui implique\(x=±1\). La dérivée n'est pas définie à\(x=0\). Par conséquent, les points critiques de\(f\) sont\(x=0,1,−1\). Le point\(x=0\) étant un point final, nous l'avons déjà évalué\(f(0)\) à l'étape 1. Le point n'\(x=−1\)est pas dans l'intervalle d'intérêt, il suffit donc d'évaluer\(f(1)\). Nous constatons que

\(f(1)=−2.\)

Étape 3. Nous comparons les valeurs trouvées aux étapes 1 et 2, dans le tableau suivant.

\(x\)	\(f(x)\)	Conclusion
\(0\)	\(0\)	Maximum absolu
\(1\)	\(−2\)	Minimum absolu
\(2\)	\(−0.762\)

Nous concluons que le maximum absolu de l'\(f\)intervalle\([0, 2]\) est nul et qu'il se produit à\(x=0\). Le minimum absolu est\(−2,\) et il se produit\(x=1\) comme indiqué sur la figure\(\PageIndex{9}\).

La fonction f (x) = x^2 — 3x^ (2/3) est représentée graphiquement de (0, 0) à (2, −0,762), son minimum étant marqué à (1, −2). — Figure\(\PageIndex{9}\) : Cette fonction possède un maximum absolu à une extrémité de l'intervalle.

Exercice\(\PageIndex{2}\)

Détermine le maximum absolu et le minimum absolu de l'\(f(x)=x^2−4x+3\)intervalle\([1,4]\).

Allusion: Recherchez les points critiques. Évaluez\(f\) à tous les points critiques et aux points de terminaison.

Réponse: Le maximum absolu est\(3\) et se produit à\(x=4\). Le minimum absolu est\(−1\) et se produit à\(x=2\).

À ce stade, nous savons comment localiser les extrêmes absolus pour des fonctions continues sur des intervalles fermés. Nous avons également défini des extrêmes locaux et déterminé que si une fonction\(f\) possède un extremum local en un point\(c\), il\(c\) doit s'agir d'un point critique de\(f\). Cependant, le\(c\) fait d'être un point critique n'est pas une condition suffisante\(f\) pour avoir un extremum local à\(c\). Plus loin dans ce chapitre, nous montrons comment déterminer si une fonction possède réellement un extremum local à un point critique. Cependant, nous devons d'abord introduire le théorème de la valeur moyenne, qui nous aidera à analyser le comportement du graphe d'une fonction.

Concepts clés

Une fonction peut avoir à la fois un maximum absolu et un minimum absolu, n'avoir qu'un seul extremum absolu ou ne pas avoir de maximum absolu ou de minimum absolu.
Si une fonction possède un extremum local, le point auquel il se produit doit être un point critique. Cependant, une fonction n'a pas besoin d'avoir un extremum local à un point critique.
Une fonction continue sur un intervalle fermé et borné possède un maximum absolu et un minimum absolu. Chaque extremum se produit à un point critique ou à un point final.

Lexique

extreum absolu: s'il\(f\) a un maximum absolu ou un minimum absolu à\(c\), nous disons qu'\(f\)il a un extremum absolu à\(c\)

maximum absolu: si\(f(c)≥f(x)\) pour tous,\(x\) dans le domaine de\(f\), disons,\(f\) a un maximum absolu à\(c\)

minimum absolu: si\(f(c)≤f(x)\) pour tous\(x\) dans le domaine de\(f\), disons,\(f\) a un minimum absolu à\(c\)

point critique: si\(f'(c)=0\) ou n'\(f'(c)\)est pas défini, nous disons que c est un point critique de\(f\)

théorème des valeurs extrêmes: si\(f\) est une fonction continue sur un intervalle fini et fermé, alors\(f\) a un maximum absolu et un minimum absolu

Théorème de Fermat: s'il\(f\) a un extremum local à\(c\), alors\(c\) est un point critique de\(f\)

extremum local: s'il\(f\) a un maximum local ou un minimum local à\(c\), nous disons qu'\(f\)il a un extremum local à\(c\)

maximum local: s'il existe un intervalle\(I\) tel que\(f(c)≥f(x)\) pour tous\(x∈I\), on dit qu'\(f\)il a un maximum local à\(c\)

minimum local: s'il existe un intervalle\(I\) tel que,\(f(c)≤f(x)\) pour tous\(x∈I\), on dit qu'\(f\)il a un minimum local à\(c\)