4.2 : Approximations et différentiels linéaires
- Page ID
- 197647
- Décrivez l'approximation linéaire d'une fonction en un point.
- Ecrivez la linéarisation d'une fonction donnée.
- Dessinez un graphique qui illustre l'utilisation de différentiels pour approximer la variation d'une quantité.
- Calculez l'erreur relative et l'erreur en pourcentage à l'aide d'une approximation différentielle.
Nous venons de voir comment les dérivés nous permettent de comparer des quantités apparentées qui évoluent dans le temps. Dans cette section, nous examinons une autre application des dérivées : la capacité d'approximer des fonctions localement par des fonctions linéaires. Les fonctions linéaires sont les plus faciles à utiliser. Elles constituent donc un outil utile pour approximer les valeurs des fonctions. De plus, les idées présentées dans cette section sont généralisées plus loin dans le texte lorsque nous étudions comment approximer des fonctions par des polynômes de degré supérieur Introduction aux séries et fonctions de puissance.
Approximation linéaire d'une fonction en un point
Prenons l'exemple d'une fonction\(f\) qui est dérivable à un point donné\(x=a\). Rappelons que la tangente au graphe de\(f\) at\(a\) est donnée par l'équation
\[y=f(a)+f'(a)(x−a). \nonumber \]
Par exemple, considérez la fonction\(f(x)=\frac{1}{x}\) à\(a=2\). Puisque\(f\) est différenciable à\(x=2\) et\(f'(x)=−\frac{1}{x^2}\), nous le voyons\(f'(2)=−\frac{1}{4}\). Par conséquent, la tangente au graphe de\(f\) at\(a=2\) est donnée par l'équation
\[y=\frac{1}{2}−\frac{1}{4}(x−2). \nonumber \]
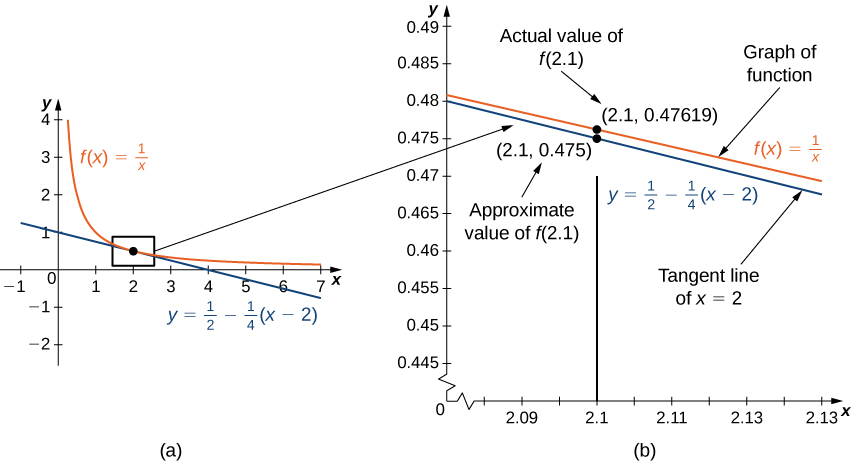
La figure\(\PageIndex{1a}\) montre un graphique\(f(x)=\frac{1}{x}\) avec la tangente à\(f\) at\(x=2\). Notez que pour la\(2\) valeur\(x\) proche, le graphique de la tangente est proche du graphe de\(f\). Par conséquent, nous pouvons utiliser l'équation de la tangente\(f(x)\) pour obtenir une approximation de la valeur\(x\) proche\(2\). Par exemple\(x=2.1\), si la\(y\) valeur du point correspondant sur la tangente est
\[y=\frac{1}{2}−\frac{1}{4}(2.1−2)=0.475. \nonumber \]
La valeur réelle de\(f(2.1)\) est donnée par
\[f(2.1)=\frac{1}{2.1}≈0.47619. \nonumber \]
Par conséquent, la droite tangente nous donne une assez bonne approximation de\(f(2.1)\) (Figure\(\PageIndex{1b}\)). Cependant, notez que pour des valeurs de\(x\) loin\(2\), l'équation de la tangente ne nous donne pas une bonne approximation. Par exemple\(x=10\), si la\(y\) valeur -du point correspondant sur la tangente est
\[y=\frac{1}{2}−\frac{1}{4}(10−2)=\frac{1}{2}−2=−1.5, \nonumber \]
alors que la valeur de la fonction at\(x=10\) est\(f(10)=0.1.\)
En général, pour une fonction dérivable\(f\), l'équation de la tangente à\(f\) at\(x=a\) peut être utilisée\(f(x)\) pour approximer la valeur\(x\) proche\(a\). Par conséquent, nous pouvons écrire
\(f(x)≈f(a)+f'(a)(x−a)\)pour\(x\) près de\(a\).
Nous appelons la fonction linéaire
\[L(x)=f(a)+f'(a)(x−a) \label{linearapprox} \]
l'approximation linéaire, ou approximation de la ligne tangente, de\(f\) at\(x=a\). Cette fonction\(L\) est également connue sous le nom de linéarisation de\(f\) at\(x=a.\)
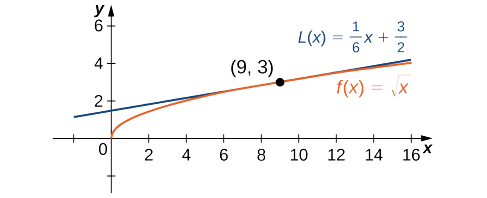
Pour montrer l'utilité de l'approximation linéaire, nous allons voir comment trouver l'approximation linéaire pour\(f(x)=\sqrt{x}\)\(x=9.\)
Trouvez l'approximation linéaire de\(f(x)=\sqrt{x}\) at\(x=9\) et utilisez-la pour effectuer une estimation\(\sqrt{9.1}\).
Solution
Puisque nous recherchons l'approximation linéaire à l'\(x=9,\)aide de l'équation \ ref {linearapprox}, nous savons que l'approximation linéaire est donnée par
\[L(x)=f(9)+f'(9)(x−9). \nonumber \]
Nous devons trouver\(f(9)\) et\(f'(9).\)
\(f(x)=\sqrt{x}⇒f(9)=\sqrt{9}=3\)
\(f'(x)=\frac{1}{2\sqrt{x}}⇒f'(9)=\frac{1}{2\sqrt{9}}=\frac{1}{6}\)
Par conséquent, l'approximation linéaire est donnée par la figure\(\PageIndex{2}\).
\[L(x)=3+\frac{1}{6}(x−9) \nonumber \]
En utilisant l'approximation linéaire, nous pouvons estimer\(\sqrt{9.1}\) en écrivant
\[\sqrt{9.1}=f(9.1)≈L(9.1)=3+\frac{1}{6}(9.1−9)≈3.0167. \nonumber \]
Analyse
À l'aide d'une calculatrice, la valeur comprise\(\sqrt{9.1}\) entre 1 et 4 décimales est de\(3.0166\). La valeur donnée par l'approximation linéaire,\(3.0167\), est très proche de la valeur obtenue avec un calculateur. Il semble donc que l'utilisation de cette approximation linéaire soit une bonne méthode d'estimation\(\sqrt{x}\), au moins pour x near\(9\). En même temps, il peut sembler étrange d'utiliser une approximation linéaire lorsqu'il suffit d'appuyer sur quelques boutons d'une calculatrice pour évaluer\(\sqrt{9.1}\). Cependant, comment évalue-t-on le calculateur\(\sqrt{9.1}\) ? Le calculateur utilise une approximation ! En fait, les calculateurs et les ordinateurs utilisent des approximations en permanence pour évaluer des expressions mathématiques ; ils n'utilisent que des approximations de plus haut degré.
Trouvez l'approximation linéaire locale de\(f(x)=\sqrt[3]{x}\) at\(x=8\). Utilisez-le pour obtenir une valeur approximative\(\sqrt[3]{8.1}\) de cinq décimales.
- Allusion
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Réponse
-
\(L(x)=2+\frac{1}{12}(x−8);\)\(2.00833\)
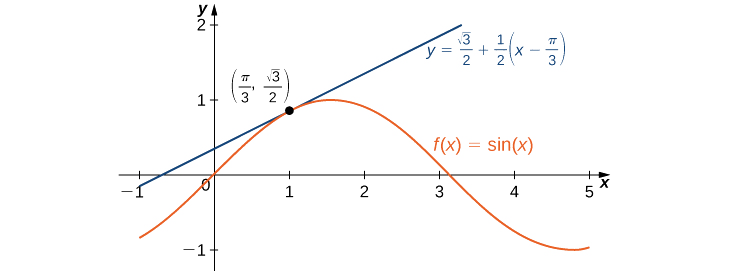
Trouvez l'approximation linéaire de\(f(x)=\sin x \) at\(x=\frac{π}{3}\) et utilisez-la pour obtenir une approximation\(\sin(62°).\)
Solution
Nous notons d'abord que puisque\(\frac{π}{3}\) rad est équivalent à\(60°\), l'utilisation de l'approximation linéaire at\(x=π/3\) semble raisonnable. L'approximation linéaire est donnée par
\(L(x)=f(\frac{π}{3})+f'(\frac{π}{3})(x−\frac{π}{3}).\)
Nous voyons que
\(f(x)=\sin x ⇒f(\frac{π}{3})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}\)
\(f'(x)=\cos x ⇒f'(\frac{π}{3})=\cos(\frac{π}{3})=\frac{1}{2}\)
Par conséquent, l'approximation linéaire de\(f\) at\(x=π/3\) est donnée par la figure\(\PageIndex{3}\).
\(L(x)=\frac{\sqrt{3}}{2}+\frac{1}{2}(x−\frac{π}{3})\)
Pour effectuer une estimation à\(\sin(62°)\) l'aide de\(L\), nous devons d'abord les\(62°\) convertir en radians. Nous avons\(62°=\frac{62π}{180}\) des radians, donc l'estimation pour\(\sin(62°)\) est donnée par
\(\sin(62°)=f(\frac{62π}{180})≈L(\frac{62π}{180})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{62π}{180}−\frac{π}{3})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{2π}{180})=\frac{\sqrt{3}}{2}+\frac{π}{180}≈0.88348.\)
Trouvez l'approximation linéaire pour\(f(x)=\cos x \) at\(x=\frac{π}{2}.\)
- Allusion
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Réponse
-
\(L(x)=−x+\frac{π}{2}\)
Des approximations linéaires peuvent être utilisées pour estimer les racines et les puissances. Dans l'exemple suivant, nous trouvons l'approximation linéaire de\(f(x)=(1+x)^n\) at\(x=0\), qui peut être utilisée pour estimer les racines et les puissances de nombres réels proches de\(1\). La même idée peut être étendue à une fonction de la forme\(f(x)=(m+x)^n\) pour estimer les racines et les puissances à proximité d'un nombre différent\(m\).
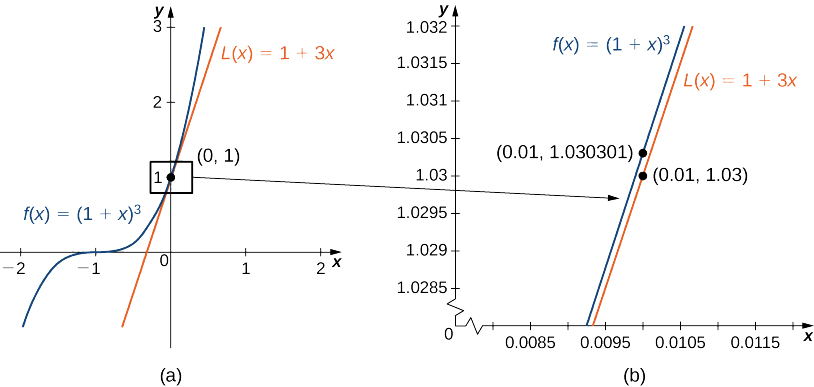
Détermine l'approximation linéaire de\(f(x)=(1+x)^n\) at\(x=0\). Utilisez cette approximation pour estimer\((1.01)^3.\)
Solution
L'approximation linéaire at\(x=0\) est donnée par
\(L(x)=f(0)+f'(0)(x−0).\)
Parce que
\(f(x)=(1+x)^n⇒f(0)=1\)
\(f'(x)=n(1+x)^{n−1}⇒f'(0)=n,\)
l'approximation linéaire est donnée par la figure\(\PageIndex{4a}\).
\(L(x)=1+n(x−0)=1+nx\)
Nous pouvons faire des\((1.01)^3\) approximations en évaluant\(L(0.01)\) quand\(n=3\). Nous concluons que
\((1.01)^3=f(1.01)≈L(1.01)=1+3(0.01)=1.03.\)
Trouvez l'approximation linéaire de\(f(x)=(1+x)^4\) at\(x=0\) sans utiliser le résultat de l'exemple précédent.
- Allusion
-
\(f'(x)=4(1+x)^3\)
- Réponse
-
\(L(x)=1+4x\)
Différentiels
Nous avons vu que des approximations linéaires peuvent être utilisées pour estimer les valeurs des fonctions. Ils peuvent également être utilisés pour estimer l'ampleur de la modification d'une valeur de fonction à la suite d'une légère modification de l'entrée. Pour en discuter plus formellement, nous définissons un concept connexe : les différentiels. Les différentiels nous permettent d'estimer l'ampleur de la modification d'une fonction à la suite d'une légère modification des valeurs d'entrée.
Lorsque nous avons examiné les dérivées pour la première fois, nous avons utilisé la notation de Leibniz\(dy/dx\) pour représenter la\(y\) dérivée de par rapport à\(x\). Bien que nous ayons utilisé les expressions\(dy\) et\(dx\) dans cette notation, elles n'avaient pas de sens en elles-mêmes. Nous voyons ici le sens des expressions\(dy\) et\(dx\). Supposons que\(y=f(x)\) c'est une fonction dérivable. \(dx\)Soit une variable indépendante à laquelle on peut attribuer n'importe quel nombre réel différent de zéro, et définissez la variable dépendante\(dy\) par
\[dy=f'(x)\,dx. \label{diffeq} \]
Il est important de noter que cela\(dy\) dépend à la fois de\(x\) et\(dx\). Les expressions\(dy\) et\(dx\) sont appelées différentiels. Nous pouvons diviser les deux côtés de l'équation \ ref {diffeq} par\(dx,\) laquelle les rendements
\[\frac{dy}{dx}=f'(x). \label{inteq} \]
C'est l'expression familière que nous avons utilisée pour désigner un dérivé. L'équation \ ref {inteq} est connue sous le nom de forme différentielle de l'équation \ ref {diffeq}.
Pour chacune des fonctions suivantes, trouvez\(dy\) et évaluez quand\(x=3\) et\(dx=0.1.\)
- \(y=x^2+2x\)
- \(y=\cos x \)
Solution
L'étape clé consiste à calculer la dérivée. Lorsque nous l'avons, nous pouvons l'obtenir\(dy\) directement.
a. Puisque\(f(x)=x^2+2x,\) nous savons\(f'(x)=2x+2\), et donc
\(dy=(2x+2)\,dx.\)
Quand\(x=3\) et\(dx=0.1,\)
\(dy=(2⋅3+2)(0.1)=0.8.\)
b. Puisque\(f(x)=\cos x , f'(x)=−\sin(x).\) cela nous donne
\(dy=−\sin x \,dx.\)
Quand\(x=3\) et\(dx=0.1,\)
\(dy=−\sin(3)(0.1)=−0.1\sin(3).\)
Pour\(y=e^{x^2}\), trouvez\(dy\).
- Allusion
-
\(dy=f'(x)\,dx\)
- Réponse
-
\(dy=2xe^{x^2}dx\)
Nous connectons maintenant les différentiels à des approximations linéaires. Les différentiels peuvent être utilisés pour estimer la variation de la valeur d'une fonction résultant d'une légère modification des valeurs d'entrée. Considérez une fonction\(f\) qui est dérivable à un point\(a\). Supposons que l'entrée\(x\) change légèrement. Nous nous intéressons à l'ampleur de la\(y\) variation de la sortie. Si le\(x\) changement passe de\(a\) à\(a+dx\), alors le changement dans\(x\) est\(dx\) (également indiqué\(Δx\)), et le changement dans\(y\) est donné par
\[Δy=f(a+dx)−f(a). \nonumber \]
Cependant\(y\), au lieu de calculer la variation exacte de, il est souvent plus facile d'approximer la variation en\(y\) utilisant une approximation linéaire. Car\(x\) near\(a, f(x)\) peut être approximé par l'approximation linéaire (Equation \ ref {linearapprox})
\[L(x)=f(a)+f'(a)(x−a). \nonumber \]
Par conséquent, s'\(dx\)il est petit,
\[f(a+dx)≈L(a+dx)=f(a)+f'(a)(a+dx−a). \nonumber \]
C'est-à-dire
\[f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx. \nonumber \]
En d'autres termes, la variation réelle de la fonction\(f\) si elle\(x\) augmente de\(a\) à\(a+dx\) est approximativement la différence entre\(L(a+dx)\) et\(f(a)\), où\(L(x)\) est l'approximation linéaire de\(f\) at\(a\). Par définition de\(L(x)\), cette différence est égale à\(f'(a)\,dx\). En résumé,
\[Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx=dy. \nonumber \]
Par conséquent, nous pouvons utiliser le différentiel\(dy=f'(a)\,dx\) pour approximer la variation de\(y\) si elle\(x\) augmente de\(x=a\) à\(x=a+dx\). Nous pouvons le voir dans le graphique suivant.
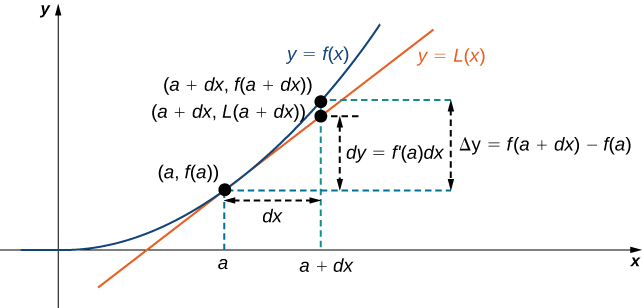
Nous allons maintenant voir comment utiliser les différentiels pour approximer la variation de la valeur de la fonction qui résulte d'une légère modification de la valeur de l'entrée. Notez que le calcul avec des différentiels est beaucoup plus simple que le calcul des valeurs réelles des fonctions et que le résultat est très proche de ce que nous obtiendrions avec un calcul plus précis.
\(Δy\)Let\(y=x^2+2x.\) Compute et\(dy\) à\(x=3\) if\(dx=0.1.\)
Solution
La variation réelle en\(y\) cas de\(x\) passage de\(x=3\) à\(x=3.1\) est donnée par
\(Δy=f(3.1)−f(3)=[(3.1)^2+2(3.1)]−[3^2+2(3)]=0.81.\)
La variation approximative\(y\) est donnée par\(dy=f'(3)\,dx\). Puisque\(f'(x)=2x+2,\) nous avons
\(dy=f'(3)\,dx=(2(3)+2)(0.1)=0.8.\)
Pour\(y=x^2+2x,\) trouver\(Δy\) et\(dy\) à\(x=3\) si\(dx=0.2.\)
- Allusion
-
\(dy=f'(3)\,dx, \;Δy=f(3.2)−f(3)\)
- Réponse
-
\(dy=1.6, \; Δy=1.64\)
Calcul du montant de l'erreur
Tout type de mesure est sujet à un certain nombre d'erreurs. Dans de nombreuses applications, certaines quantités sont calculées sur la base de mesures. Par exemple, l'aire d'un cercle est calculée en mesurant le rayon du cercle. Une erreur dans la mesure du rayon entraîne une erreur dans la valeur calculée de la surface. Nous examinons ici ce type d'erreur et étudions comment les différentiels peuvent être utilisés pour estimer l'erreur.
Prenons l'exemple\(f\) d'une fonction dont l'entrée est une quantité mesurée. Supposons que la valeur exacte de la quantité mesurée soit\(a\), mais que la valeur mesurée l'est\(a+dx\). Nous disons que l'erreur de mesure est\(dx\) (ou\(Δx\)). Par conséquent, une erreur se produit dans la quantité calculée\(f(x)\). Ce type d'erreur est connu sous le nom d'erreur propagée et est donné par
\[Δy=f(a+dx)−f(a). \nonumber \]
Comme toutes les mesures sont sujettes à un certain degré d'erreur, nous ne connaissons pas la valeur exacte d'une quantité mesurée et nous ne pouvons donc pas calculer exactement l'erreur propagée. Cependant, étant donné une estimation de la précision d'une mesure, nous pouvons utiliser des différentiels pour approximer l'erreur propagée.\(Δy.\) Plus précisément, s'il s'\(f\)agit d'une fonction dérivable à\(a\), l'erreur propagée est
\[Δy≈dy=f'(a)\,dx. \nonumber \]
Malheureusement, nous ne connaissons pas la valeur exacte,\(a.\) mais nous pouvons utiliser la valeur mesurée\(a+dx,\) et l'estimer
\[Δy≈dy≈f'(a+dx)\,dx. \nonumber \]
Dans l'exemple suivant, nous verrons comment les différentiels peuvent être utilisés pour estimer l'erreur lors du calcul du volume d'une boîte si nous supposons que la mesure de la longueur des côtés est effectuée avec une certaine précision.
Supposons que la longueur du côté d'un cube soit mesurée en\(5\) cm avec une précision de\(0.1\) cm.
- Utilisez des différentiels pour estimer l'erreur dans le volume calculé du cube.
- Calculez le volume du cube si la longueur du côté est de (i)\(4.9\) cm et (ii)\(5.1\) cm pour comparer l'erreur estimée à l'erreur potentielle réelle.
Solution
a. La mesure de la longueur des côtés est précise au\(±0.1\) centimètre près. Par conséquent,
\(−0.1≤dx≤0.1.\)
Le volume d'un cube est donné par\(V=x^3\), ce qui conduit à
\(dV=3x^2dx.\)
En utilisant la longueur de côté mesurée en\(5\) cm, nous pouvons estimer que
\(−3(5)^2(0.1)≤dV≤3(5)^2(0.1).\)
Par conséquent,
\(−7.5≤dV≤7.5.\)
b. Si la longueur du côté est réellement en\(4.9\) cm, le volume du cube est
\(V(4.9)=(4.9)^3=117.649\text{cm}^3.\)
Si la longueur du côté est réellement en\(5.1\) cm, le volume du cube est
\(V(5.1)=(5.1)^3=132.651\text{cm}^3.\)
Par conséquent, le volume réel du cube se situe entre\(117.649\) et\(132.651\). Puisque la longueur du côté est mesurée à 5 cm, le volume calculé est\(V(5)=5^3=125.\) donc, l'erreur dans le volume calculé est
\(117.649−125≤ΔV≤132.651−125.\)
C'est-à-dire
\(−7.351≤ΔV≤7.651.\)
Nous constatons que l'erreur estimée\(dV\) est relativement proche de l'erreur potentielle réelle dans le volume calculé.
Estimez l'erreur dans le volume calculé d'un cube si la longueur du côté est mesurée en\(6\) cm avec une précision de\(0.2\) cm.
- Allusion
-
\(dV=3x^2dx\)
- Réponse
-
La mesure du volume est précise à l'intérieur\(21.6\,\text{cm}^3\).
L'erreur de mesure\(dx\ (=Δx)\) et l'erreur propagée\(Δy\) sont des erreurs absolues. Nous nous intéressons généralement à la taille d'une erreur par rapport à la taille de la quantité mesurée ou calculée. Étant donné une erreur absolue\(Δq\) pour une quantité donnée, nous définissons l'erreur relative comme\(\frac{Δq}{q}\) suit : où\(q\) est la valeur réelle de la quantité. L'erreur en pourcentage est l'erreur relative exprimée en pourcentage. Par exemple, si nous mesurons la hauteur d'une échelle lorsque la hauteur réelle est\(62\) dedans, l'erreur absolue est de 1 pouce mais l'erreur relative est de\(\frac{1}{62}=0.016\), ou\(1.6\%\).\(63\) En comparaison, si nous mesurons la largeur d'un morceau de carton\(8.25\) dedans, lorsque la largeur réelle est\(8\) dedans, notre erreur absolue est\(\frac{1}{4}\) dedans, alors que l'erreur relative est\(\frac{0.25}{8}=\frac{1}{32}\), ou\(3.1\%.\) Par conséquent, l'erreur en pourcentage dans la mesure du carton est plus grande, même bien que\(0.25\) dans. soit moins que\(1\) dedans.
Un astronaute utilisant une caméra mesure le rayon de la Terre en\(4000\) mi avec une erreur de\(±80\) mi. Utilisons des différentiels pour estimer l'erreur relative et en pourcentage liée à l'utilisation de cette mesure du rayon pour calculer le volume de la Terre, en supposant que la planète est une sphère parfaite.
Solution : Si la mesure du rayon est précise à l'intérieur,\(±80,\) nous avons
\(−80≤dr≤80.\)
Puisque le volume d'une sphère est\(V=(\frac{4}{3})πr^3,\) donné par
\(dV=4πr^2dr.\)
En utilisant le rayon mesuré de\(4000\) mi, nous pouvons estimer
\(−4π(4000)^2(80)≤dV≤4π(4000)^2(80).\)
Pour estimer l'erreur relative, considérez\(\dfrac{dV}{V}\). Comme nous ne connaissons pas la valeur exacte du volume\(V\), utilisez le rayon mesuré\(r=4000\) mi pour l'estimer\(V\). Nous obtenons\(V≈(\frac{4}{3})π(4000)^3\). Par conséquent, l'erreur relative satisfait
\(\frac{−4π(4000)^2(80)}{4π(4000)^3/3}≤\dfrac{dV}{V}≤\frac{4π(4000)^2(80)}{4π(4000)^3/3},\)
ce qui simplifie
\(−0.06≤\dfrac{dV}{V}≤0.06.\)
L'erreur relative est\(0.06\) et le pourcentage d'erreur est\(6\%\).
Déterminez le pourcentage d'erreur si le rayon de la Terre est mesuré à\(3950\) mi avec une erreur de\(±100\) mi.
- Allusion
-
Utilisez le fait que\(dV=4πr^2dr\) pour trouver\(dV/V\).
- Réponse
-
\(7.6\%\)
Concepts clés
- Une fonction dérivable\(y=f(x)\) peut être approximée\(a\) par la fonction linéaire
\(L(x)=f(a)+f'(a)(x−a).\)
- Pour une fonction\(y=f(x)\), si elle\(x\) passe de\(a\) à\(a+dx\), alors
\(dy=f'(x)\,dx\)
est une approximation de la variation de\(y\). Le changement réel\(y\) est
\(Δy=f(a+dx)−f(a).\)
- Une erreur de mesure\(dx\) peut entraîner une erreur dans une quantité calculée\(f(x)\). L'erreur dans la quantité calculée est connue sous le nom d'erreur propagée. L'erreur propagée peut être estimée par
\(dy≈f'(x)\,dx.\)
- Pour estimer l'erreur relative d'une quantité donnée\(q\), nous estimons\(\frac{Δq}{q}\).
Équations clés
- Approximation linéaire
\(L(x)=f(a)+f'(a)(x−a)\)
- Un différentiel
\(dy=f'(x)\,dx\)
Lexique
- différentiel
- le différentiel\(dx\) est une variable indépendante à laquelle on peut attribuer n'importe quel nombre réel non nul ; le différentiel\(dy\) est défini comme\(dy=f'(x)\,dx\)
- forme différentielle
- étant donné une fonction dérivable,\(y=f'(x),\) l'équation\(dy=f'(x)\,dx\) est la forme différentielle de la\(y\) dérivée de par rapport à\(x\)
- approximation linéaire
- la fonction linéaire\(L(x)=f(a)+f'(a)(x−a)\) est l'approximation linéaire de\(f\) at\(x=a\)
- erreur en pourcentage
- l'erreur relative exprimée en pourcentage
- erreur propagée
- l'erreur qui se traduit par une quantité calculée\(f(x)\) résultant d'une erreur de mesure\(dx\)
- erreur relative
- étant donné une erreur absolue\(Δq\) pour une quantité donnée,\(\frac{Δq}{q}\) est l'erreur relative.
- approximation de la ligne tangente (linéarisation)
- étant donné que l'approximation linéaire de\(f\) at\(x=a\) est définie à l'aide de l'équation de la tangente, l'approximation linéaire de\(f\) at\(x=a\) est également connue sous le nom d'approximation de la droite tangente à\(f\) at\(x=a\)


